Псевдоевклидово пространство

Содержание.

TOC o "1-1" h z u ВВЕДЕНИЕ. 2<

ГЛАВА I.АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ПСЕВДОЕВКЛИДОВЫХ И ПОЛУЕВКЛИДОВЫХ ПРОСТРАНСТВ

I.1.ОБОБЩЕННОЕ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. ПСЕВДОЕВКЛИДВы И ПОЛУЕВКЛИДОВЫ ПРОСТРАНСТВА. 3<

I.2.ПСЕВДОЕВКЛИДОВА ПЛОСКОСТЬ (ПЛОСКОСТЬ МИНКОВСКОГО) 5<

I.3.Движение плоскости МИНКОВСКОГО. 7<

I.4.Угол между векторами иа прямыми. 10<

I.5.ТРЕУГОЛЬНИК В ПЛОСКОСТИ МИНКОВСКОГО. 13<

I.6.ЧИСЛОВАЯ МОДЕЛЬ ПЛОСКОСТИ МИНКОВСКОГО. 15<

Глава II.АКСИОМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ПОЛУЕВКЛИДОВЫХ И ПСЕВДОЕВКЛИДОВЫХ ПРОСТРАНСТВ.

II.Аксиоматическое определение псевдоевклидовых и полуевклидовых векторных пространств. 19<

II.2.Полуевклидовы и псевдоевклидовы точечные пространства 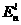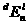22<

Глава <.ПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО

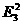
.1.Псевдоевклидово пространство (пространство Минковского) 24<

.2.Наглядная модель пространства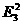..... а

Глава IV Гиперболическая плоскость Г₂.

IV.1.Гиперболическая плоскость Г₂. 28<

Приложения. 32<

Список литературы. 33<

Глава <.ПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО

Список литературы.

ндреева З.И, Шеремет Г.Г. Псевдоевклидова плоскость (плоскость Минковского) //в сб. Актуальные проблемы обучения математике т.3: Материалы Всероссийскойа научно-практической конференции.- Орел: Изд. ОГУ,2002.

Розенфельд Б.А. Неевклидовы пространства.-М.:Наука,1978.

Яглом И.М. Принцип относительности Галилея и неевклидова геометрия.-М.:, Наука, 1972.