Задача остовных деревьев в kЦсвязном графе
Министерство Науки и Образования
Республики Молдова
Молдавский Государственный ниверситет
Кафедра Информатики и Дискретной Оптимизации
Дипломная работа:
Задача остовных деревьев в kЦсвязном графе
работу выполнил
ст. V курса гр.52MI
Жуков В.
Работу приняла:
Dr.физЦмат. наук
Присэкару В.К.
КишиневЦ2002
Содержание:
Введени.2
Глава I Основные определения.4
з1 Основные определения теории графов...4
з2 Матрицы смежности и инцидентности..10
з3 Деревья..13
Глава II Связность 18
з4 Вершинная связность и реберная вязность18
з5 Двусвязные графы....22
з6 Теорема Менгера.Е.32
Глава Выделение k непересекающихся остовных деревьев
2kЦреберно связном граф36
з7 Построение k непересекающихся остовных деревьев......Е37
з8 Необходимость условия 
 ..Е.40
..Е.40
з9 Текст программы..Е42
Вывод..51
Введение
Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждение о Кенигсбергских мостах. Однако эта статья Эйлера 1736 года была единственной в течение почти ста лет. Интерес к проблемам теории графов возродился около середины прошлого столетия и был сосредоточен главным образом в Англии. Имелось много причин для такого оживления изучения графов. Естественные науки оказали свое влияние на это благодаря исследованиям электрических цепей, моделей кристаллов и структур молекул. Развитие формальной логики привело к изучению бинарных отношений в форме графов. Большое число популярных головоломок подавалось формулировкам непосредственно в терминах графов, и это приводило к пониманию, что многие задачи такого рода содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса. Наиболее знаменитая среди этих задачЦпроблема четырех красок, впервые поставленная перед математиками Де Морганом около 1850 года. Никакая проблема не вызывала столь многочисленных и остроумных работ в области теории графов. Благодаря своей простой формулировке и раздражающей неуловимости она до сих пор остается мощным стимулом исследований различных свойств графов.
Настоящее столетие было свидетелем неуклонного развития теории графов, которая за последние десять - двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, также проблем психологии и биологии.
Вследствие этого развития предмет теории графов является же обширным, что все его основные направления невозможно изложить в одном томе. В настоящем первом томе предлагаемого двухтомного труда сделан акцепт на основные понятия и на результаты, вызывающие особый систематический интерес.
По теории графов имеется очень мало книг; основной была книга Д. Кёнига (1936), которая для своего времени давала превосходнейшее введение в предмет. Довольно странно, что таких книг на английском языке до сих пор не было, несмотря на то, что многие важнейшие результаты были получены американскими и английскими авторами.
Глава I
Основные понятия
з1 Определения.
Предметом первых задач в теории графов были конфигурации, состоящие из точек и соединяющих их линий. В этих рассмотрениях было несущественно, прямые ли это линии или же они являются криволинейными непрерывными дугами, соединяющими две концевые точки, где расположены эти линии, являются ли они длинными или короткими. Существенно только то, что они соединяют две данные точки.
Это приводит к определению графа как абстрактного математического понятия. Рассматривая множество V, состоящее из соединенных некоторым образом точек. Назовем V множеством вершин и элементы
G<=G(V) (1.1)
c множеством вершин V есть некоторое семейство сочетаний, или пар вида
E=(a, b),
указывающие, какие вершины являются соседними. В соответствии с геометрическим представлением графа каждая конкретная пара (1.2) называется ребром графа; вершины
Можно использовать и другой подход. Если даны два множества V1 и V2 то можно образовать множество всех пар
( Это множество пар называется произведением и обозначается через V1´V2. В нашем случае каждая пара вершин ( Это определение графа должно быть дополнено в одном важном отношении. В определении ребра (1.2) можно принимать или не принимать во внимание порядок расположения двух его концов. Если этот порядок несуществен, т.е. если E=(a,
b)=(b, a), то говорят, что Е есть неориентированное ребро; если же этот порядок существен, то Е называется ориентированным ребром. В последнем случае называется также начальной вершиной, В приложениях граф обычно интерпретируется как сеть, в которой вершинами G являются злы.
Два зла
Граф называется неориентированным, если каждое его ребро не ориентированно, и ориентированным,
если ориентированны все его ребра. На рис.1.2 приведены примеры неориентированных графов. На рис 1.3 изображены ориентированны графы. В ряде случаев естественно рассматривать смешанные графы, имеющие как ориентированные, така неориентированные ребра. Например, план города можно рассматривать как граф, в котором ребра представляют лицы, вершины - перекрестки; при этом по одним лицам может допускаться лишь одностороннее движение, и тогда на соответствующих ребрах вводится ориентация; по другим лицам движение двустороннее, и на соответствующих ребрах же никакой ориентации не вводится. Мы же отмечали, что при фактическом изображении графа имеется большая свобода в размещении вершин и в выборе формы соединяющих их дуг. Поэтому может оказаться,
что один и тот же граф представляется совсем различными чертежами. Будем говорить, что два графа G и G<' изоморфны, если существует такое взаимно однозначное соответствие между множествами их вершин V и VТ, что вершины соединены ребрами в одном из графов в том и только том случае, когда соответствующие им вершины соединены в другом графе. Если ребра ориентированы, то их направления также должны соответствовать друг другу. На рис 1.2 приведены примеры изоморфных графов, образованных ребрами и вершинами правильных многогранников. Вершина не инцидентна никакому ребру, называется изолированной.
При определение множества вершин V данного графа часто имеет смысл учитывать только неизолированные вершины. Граф, состоящий только из изолированных вершин,
называется нульЦграфом и может быть обозначен через 0. другим важным случаем является (неориентированный) полный граф U=U(V),
(1.3) ребрами которого являются всевозможные пары (1.2) для двух различных вершин
В ориентированном полном графе U(d) имеются пары ребер, по одному в каждом направлении. Соединяющие любые две различные вершины
Сформулированное выше определение графа, вместе с соответствующим изображением, достаточно для многих задач. Однако для некоторых целей желательно понятие графа несколько расширить. L=(a, a). (1.4) Такое ребро (1.4) будет называться петлей. При изображении графа петля будет представляться замкнутой дугой, возвращающейся в вершину и не проходящей через другие вершины
(рис 1.5). Петля обычно считается неориентированной. Можно расширить полный граф U в (1.3) до полного графа с петлями U0, добавляя петлю в каждой вершине,
так что ребрами U0 являются все пары (1.2), где допускается и ВоЦвторых,
можно расширить понятие графа, допуская, чтобы пара вершин соединялась несколькими различными ребрами Ei=(a,
b)i,
(1.5) как это изображено на рис. 1.6. Для ориентированного графа две вершины
Ei=(a,
b)i, (рис. 1.7). Чтобы проиллюстрировать случай, для которого эти понятия оказываются естественными,
рассмотрим какоеЦлибо командное соревнование, например турнирную таблицу лиги бейсбола. Вершинами соответствующего графа являются команды. Пара команд А и В связывается ребром каждый раз, когда они сыграли. Если А выиграла у В, то это ребро будем ориентировать от А к В. если В выиграла у А, то противоположном направлении; в случае ничьей ребро будет неориентированным. Для каждогоа графа G существует обратный граф G*, получаемый изменением ориентации каждого из ребер G на противоположную. Для каждого ориентированного графа существует также соотнесенный неориентированный граф Gu, ребрами которого являются ребра G, но же без ориентаций. Иногда добно превратить неориентированный граф G в ориентированный граф Gd при помощи процесса двоения, состоящего в замене каждого ребра G парой с теми же концами и приписывании им противоположных ориентаций. Граф называется плоским, если он может быть изображен на плоскости так что все пересечения ребер являются вершинами G. Граф на рис 1.8а плоский, на рис 1.8б неплоский. з2. Матрицы смежности и инцидентности. В з1 мы определили ребро Е (1.2) графа G (1.1) как элемент или точку ( Если G имеет кратные ребра, то числа 0 и 1 в клетках ( Сказанное приводит к дальнейшему расширению понятия графа, использующему же все конечные или бесконечные матрицы, элементами которых являются вещественные неотрицательные числа. Такие матрицы встречаются в различных областях математики. Например, стохастические матрицы - в теории вероятностей и в теоретической физике. Где рассматриваемая система имеет некоторое множество V возможных состояний, и любая пара состояний ( Графы могут быть также описаны матрицами другого вида. Всякий граф состоит из объектов двух типовЦвершин и ребер. Можно построить матицу M1(G), строки которой соответствуют вершинам, столбцыЦребрам. На месте (а, Е) в этой матрице поместим значение Введем,
наконец, матрицу смежности ребер I(G), в которой и строки и столбцы отвечают ребрам G. Для простоты предположим. Что G не имеет петель, а ребра неориентированные и однократные. На месте (E, EТ) в I(G) поместим Можно встать и на другую точку зрения и рассматривать I(G) как матрицу смежности вершин для нового графа, также обозначаемого через I(G), вершинами которого являются ребра Е графа G, ребрамиЦпары (E, EТ) с Фактическое построение смежности графа I(G) по чертежу графа G просто. На каждом ребре Е выбираем фиксированную точку еЕ,
например середину Е. Пару таких вершин (е, еТ) соединяем новым ребром, принадлежащим I(G), тогда и только тогда, когда соответствующие ребра Е и ЕТ имеют общую вершину в G. Рис. 2.2 дает это построение для графа тетраэдра; смежностным графом для него является граф октаэдра. Предположим, то в вершине е сходится r(е) ребер Е=(е, еТ) из G. Тогда в I(G) середина I(G)= На полные графы U( Предположим, что,
наоборот, для графа G1 существует такое разложение (2.1) на полные графы, что пара (U( Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или) лесом. Таким образом, компонентами леса являются деревья. На рис.12 изображены все деревья шестого порядка. Существует несколько вариантов определения дерева;
некоторые из них отражены в следующей теореме. Теорема 3.1 Для графа следующие тверждения эквивалентны: 1)
G - дерево; 2)
G - связный граф и 3)
G - ациклический граф и 4)
любые две несовпадающие вершины графа соединяет единственная простая цепь; 5)
G - ациклический граф,
обладающий тем свойством, что если какуЦлибо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл. 1) каждая из которых есть дерево. Пусть дерево Ti является ( mi<= m=m1+m2+1=(n1-1)+(n2-1)+1=(n1+n2)-1=n-1. 2) 3) n<-1= т.е. к=1. Итак, GЦсвязный граф и потому любые несовпадающие вершины
4) 5) Следствие 3.2. В любом дереве порядка Пусть d1, d2, Е, dn
(2) Цстепенная последовательность дерева. Тогда (лемма о рукопожатиях) и все di<>0. Следовательно, хотя бы два числа из последовательности (2) равны 1. Пусть Цостовный подграф поизвольного гафа G. Если на каждой области связности графа G графом Н порождает дерево, то Н называется остовом (или каркасом) графа G. очевидно, что в каждом графе существует остов: разрушая в каждой компоненте циклы, т.е. даляя лишние ребра, придем к остову. Остов в графе легко найти с помощью поиска в ширину. Следствие 3.3. число ребер произвольного графа G, которые необходимо удалить для получения остова, не зависит от последовательности их даления и равно Если ( Число Очевидны три следствия 13.4-13.6. Следствие 3.4. Граф G является лесом тогда и только тогда, когда Следствие 3.5. граф G имеет единственный цикл тогда и только тогда, когда Следствие 3.6.
Граф, в котором число ребер не меньше,
чем число вершин, содержит цикл. Утверждение 3.7. Если S и Т Цдва остова графа G, то для любого ребра е1
графа S существует такое ребро е2 графа Т, что граф также является остовом. Доказательство Не ограничивая общности, будем считать граф G связным. Граф имеет ровно две области связности;
пусть это будут А и В. Поскольку граф Т связен, то в нем существует ребро е2, один из концов которого входит в А, другой - в В. Граф Н=S<- Теорема 13.8. Центр любого дерева состоит из одной или из двух смежных вершин. Очевидно,
что концевые вершины дерева Т являются центральными только для T=K1 или T=K2. Пусть Т дерево порядка Глава II Связность Связный граф был определен как граф, у которого любые две вершины соединены цепью. Так, оба графа Кn
и Cn связны, однако интуитивно ясно, что при n<>3 граф Kn сильнее связен, чем Cn.
В этой главе вводится и исследуются понятия, характеризующие степень связности графа. з4 Вершинная связность и реберная связность. Прежде чема ввести понятия вершинной и реберной связности, рассмотрим однуа математическую модель, возникающую, в частности, при проектировании и анализе сетей ЭВМ. Имеется сеть, состоящая из центров хранения и переработки информации. Некоторые пары центров соединены каналами. Обмен информацией между любыми двумя центрами осуществляется либо непосредственно по соединяющему их каналу, если он есть, либо через другие каналы и центры. Сеть считается исправной, если каждая пара центров в состоянии обмениваться информацией. Такой сети естественно сопоставить граф: вершиныЦцентры, ребрЦканалы сети. Тогда исправной сети будет соответствовать связный граф. Важным понятием является надёжность (живучесть) сети, под которой обычно подразумевают способность сети функционировать при выходе из строя одного или нескольких центров или (и)
каналов. Ясно, что менее надежной следует считать ту сеть, исправность которой нарушается при повреждении меньшего количества элементов. Оказывается,
надежность сети можно измерять на основе вводимых ниже определений. Числом вершин связности (или просто числом связности) Так,
например, Это вполне согласуется с интуитивным представлением том, что при Граф G, представленный на рис.
4.1 связен, но его связность можно нарушить, далив вершину 4. Поэтому при далении ребер {4,5}, {4,6}, {4,7}. Чтобы честь это обстоятельство, введем еще одно определение. Пусть GЦграф порядка В качестве иллюстрации снова обратимся к графу G на рис. 4.1 Здесь Определим некоторые элементы графа, играющие особую роль в дальнейших рассмотрениях. Вершина Таким образом, точки сочленения и мосты - это своего рода лузкие места графа. Граф, изображенный на рис. 4.2, имеет три точки сочленения
Понятно, что концевая вершина моста является точкой сочленения, если в графе есть другие ребра, инцидентные этой вершине. Возвращаясь к рассматриваемой в начале параграфа сети,
нетрудно заметить, что число вершинной связности и число реберной связности ее графа отражают чувствительность сети к разрушению центров и каналов соответственно, мостам и точкам сочленения отвечают наиболее язвимые места сети. Если Выясним теперь соотношения между числами Таким образом, доказана Теорема 4.1: Для любого графа G верны неравенства Граф называется кЦсвязным, если Граф G, изображенный на рис. 4.1 Цсвязен и реберноЦсвязен. Легко видеть,
что этот граф содержит подграфы, являющиеся более связными, чем сам граф.
Таков, например, подграф, порожденный множеством вершин {1, 2, 3, 4, 8}. Он Цсвязен. Чтобы честь эту и подобные ей ситуации, естественно ввести следующее определение:
максимальный Это определение иллюстрируется на рис. 4.3. На этом рисунке граф G1 имеет две Цкомпоненты, G2Цдве Цкомпоненты. Сами графы G1 и G2 являются Цкомпонентами графа G1 Теорема 4.2: Две различные кЦкомпоненты графа имеют не более чем кЦ1 общих вершин. Пусть G1 и G2 Цразличные Yi=(VGi\X)
Ясно, что |Yi| |Yi и графы G1 и G2 Hi=GiЦ(Yi связны. Так как по предложению |X<| з5 Двусвязные графы Случаям,
когда Рассмотрим вначале некоторые простые свойства Цсвязных графов, вытекающие непосредственно из определений: 1) степени вершин Цсвязного графа больше единицы; 2) если графы G1 и G2
Цсвязны и имеют не менее двух общих вершин, то граф G1 3) если граф G Цсвязен и Цпростая цепь, соединяющая две его вершины, то граф G 4) если вершина Этими свойствами мы будем пользоваться без какихЦлибо пояснений и дополнительных ссылок на них. Теорема 5.1 пусть GЦсвязный граф и |G<|>2. Тогда следующие утверждения эквивалентны: 1)
граф Цсвязен; 2)
любые две вершины графа принадлежат простому циклу; 3)
любая вершина и любое ребро принадлежат простому циклу; 4)
любые два ребра принадлежат простому циклу; 5)
для любых двух вершин
6)
для любых трех вершин 1) 2) P 3) 4) имеется требуемая цепь. 5) 6) Если в формулировке теоремы 34.1 заменить всюду слова лпростая цепь и простой цикл соответственно на слова цепь и цикл, то получим аналогичную теорему о ЦреберноЦсвязном графах. Как отмечалось выше, при решении многих задач на графах достаточно меть решать эти задачи для каждой Цсвязной компоненты графа. Поэтому представляет интерес взаимное расположение Цкомпонент в графе. Максимальные относительное включения элементы множества связных подграфов графа G, не имеющих точек сочленения, называются его блоками. Таким образом, каждый блок графа либо Цсвязен, либо совпадает с К2
или К1 (граф К1 Ц блок тогда и только тогда, когда он является связной компонентой). Связный граф без точек сочленения также называют блоком. Множество вершин блока будем называть блоковым множеством. Например,
граф, изображенный на рис. 5.2, содержит пять блоков Bi ( Утверждение 5.2. Любые два блока графа имеют не более одной общей вершины. В частности,
всякое ребро графа входит только в один его блок. Утверждение 5.3. Если блок графа содержит вершины
Эти утверждения непосредственно следуют из перечисленных в начале параграфа свойств Цсвязных графов и теоремы 5.1. Следствие 5.4. Система блоковых множеств графа является покрытием множеств его вершин.
Каждая пара блоковых множеств либо не пересекаются, либо имеют единственную общую вершину, и эта вершина является точкой сочленения графа. Следующая конструкция дает представление о структуре графа с точностью до блоков. Пусть В=В{Bi<} и С={ Утверждение 5.5. Если граф G связен, то Доказательство: Очевидно,
что из связности графа G вытекает связность граф Предположим, что Граф Блоки графа G, соответствующие концевым вершинам его Похожее представление графа можно получить, положив в основу его максимальные реберно-2-связные подграфы, т.е. максимальные связные подграфы, не содержащие мостов. Такие подграфы называют листами.
Не останавливаясь на деталях заметим следующее. Каждая вершина графа порядка На рис. 5.4
граф G имеет 5 листов L1, L2, L3, L4, L5 и 4 моста, граф G<' показывает, как связаны между собой листы графа G. Приведем некоторые результаты о трехсвязных графах, которые будут использованы в главе Планарность. Пусть GЦсвязный граф, HЦнекоторый его подграф. Простую открытую цепь. графа G назовем HЦцепь, если выполняются словия 1 ребро Лемма 5.6. Пусть GЦдвусвязный граф. Тогда для всякого его подграфа Н, содержащего более одной вершины и отличного от G, существует Ццепь графа G. Доказательство Если Цостовный подграф, то любое ребро графа
G, не входящее в EH, служит Ццепью. Пусть подграф не является остовным. Рассмотрим три попарно различные вершины Ниже для Теорема 5.7. Во всяком 3-связном графе G есть такое ребро Доказательство Если |G<|= 1) если - висячая вершина графа Guv, то 2) всякий висячий блока графа Guv, не являющийся ребром,
содержит такую пару вершин с и d, отличных от точек сочленения графа Guv, что 3) всякий блок графа Guv, имеющий ровно две точки сочленения и отличный от ребра, содержит такую вершину Обозначим через Buv максимальный по числу вершин блок графа Guv, через Покажем, что в этом случае Через Duv обозначим 1.
Duv не является цепью. Выберем в этом дереве цепь, соединяющую пару висячих вершин и проходящую через вершину, соответствующую блоку Buv.
Этой цепи соответствует последовательность B1,Е,Bp блоков графа Guv,
среди которых содержится блок Buv,
причем блоки B1 и Bp являются висячими (рис. 5.6). Пусть B<'Ц произвольный висячий блок графа Guv, отличный от B1 и Bp. Из свойств
1) и 2) вытекает существование таких отличных от точек сочленения графа Guv вершин a 2. Дерево DuvЦцепь и BuvЦблок графа Guv, не являющийся висячим.
Пусть B1,Е,Bp Ц последовательность всех блоков графа G, причем блоки B1 и BpЦвисячие, Bi существует такие отличные от точек сочленения графа Guv вершины 3. Дерево Duv Ц цепь и Buv Ц висящий блок графа Guv. Если граф Guv содержит такое ребро Guv, то последнее означает,
что граф Guv состоит из блока Buv и ребер Таким образом, показано,что во всяком связном графе G существует такое ребро Следствие 5.8. Всякий Цсвязный граф с числом вершин Доказательство также проведем от противного. Пусть, стягивая некоторое ребро Отметим без доказательства следующую теорему. Теорема 5.9. Почти все ребра двусвязны. Поскольку каждый мост инцидентен точкам сочленения графа, то из этой теоремы вытекает Следствие 5.10. Почти все графы не содержат мостов. з6 Теорема Менгера. Из теоремы
5.1 следует, что Цграф связен тогда и только тогда, когда любые две его несовпадающие вершины
Говорят, что множество вершин S разделяет несмежные вершины
К. Менгер доказал в 1927 году следующую теорему,
устанавливающую соотношение между числом непересекающихся простых цепей,
соединяющих две несмежные вершины графа, и его связностью. 1,
1,  2.
2.





 <=(a, b)j,
<=(a, b)j,

 В точку с координатами (
В точку с координатами (

 2.1
2.1 r(е) общих вершин с другими U(
r(е) общих вершин с другими U(
 а з3 Деревья
а з3 Деревья


Далее имеем
 G связен и
G связен и  кЦчисло компонент графа G. Пусть, далее,
компонента Тi является (
кЦчисло компонент графа G. Пусть, далее,
компонента Тi является ( G ациклический. Пусть
G ациклический. Пусть
 G связен. Если бы вершины
G связен. Если бы вершины

Доказательство
 (G) графа G называется наименьшее число вершин, даление которых приводит к несвязному или одновершинному графу.
(G) графа G называется наименьшее число вершин, даление которых приводит к несвязному или одновершинному графу. K1)=0,
K1)=0,  Kn)=
Kn)= G)=1. Если же попытаться нарушить связность этого графа путем даления ребер (а не вершин), то придется далить не менее трех ребер. Например, G распадается на две компоненты
G)=1. Если же попытаться нарушить связность этого графа путем даления ребер (а не вершин), то придется далить не менее трех ребер. Например, G распадается на две компоненты 
 G)=3 и, следовательно,
G)=3 и, следовательно,  G)>
G)> G). Ниже будет показано, что противоположное неравенство невозможно ни для какого графа.
G). Ниже будет показано, что противоположное неравенство невозможно ни для какого графа. G) - минимальная степень вершин графа G, то очевидно, что
G) - минимальная степень вершин графа G, то очевидно, что  G)
G)
 G), поскольку даление всех ребер, инцидентных данной вершине, приводит к величению числа компонент графа.
G), поскольку даление всех ребер, инцидентных данной вершине, приводит к величению числа компонент графа. G) и
G) и  G). Если граф G не связен или имеет мост, то очевидно, что
G). Если граф G не связен или имеет мост, то очевидно, что  G)=
G)=  G). Пусть GЦ связный граф без мостов. Выберем в этом графе множество Е1,
состоящее из
G). Пусть GЦ связный граф без мостов. Выберем в этом графе множество Е1,
состоящее из 
 (G) ребер, даление которых приводит к несвязному графу. Пусть E2
(G) ребер, даление которых приводит к несвязному графу. Пусть E2 аE1, |E2|=
аE1, |E2|= . Граф G - E2 связен и имеет мост, который обозначим через
. Граф G - E2 связен и имеет мост, который обозначим через 
 (G)<<
(G)<<

 (G)
(G)
 реберноЦкЦсвязным,
если
реберноЦкЦсвязным,
если  К1 граф Цсвязен (односвязен) тогда и только тогда,
когда он связен, Цсвязные (двусвязные) графы - это связные графы без точек сочленения, не являющиеся одновершинными.
К1 граф Цсвязен (односвязен) тогда и только тогда,
когда он связен, Цсвязные (двусвязные) графы - это связные графы без точек сочленения, не являющиеся одновершинными.
 G2. легко заметить, что Цкомпоненты графа G1 имеют одну большую вершину, Цкомпоненты графа G2Цдве общие вершины.
Следующая теорема показывает, что это обстоятельство не случайно.
G2. легко заметить, что Цкомпоненты графа G1 имеют одну большую вершину, Цкомпоненты графа G2Цдве общие вершины.
Следующая теорема показывает, что это обстоятельство не случайно.Доказательство
 VG2=X. Предположим, что |X<|
VG2=X. Предположим, что |X<| , и докажем, что тогда граф G1
, и докажем, что тогда граф G1 G2 должен быть кЦсвязным.
Для этого в данном случае достаточно показать, что он остается связным после удаления любых
G2 должен быть кЦсвязным.
Для этого в данном случае достаточно показать, что он остается связным после удаления любых  аG2), |Y<|=
аG2), |Y<|= аG2) - Y связен. Положим
аG2) - Y связен. Положим  Y,
Y,
 Y.
Y.
 Y2
Y2 Y3.
Y3.Поскольку
 Y3|
Y3| Ц1,
Ц1,  Y3),
Y3),
 , то X<\Y3
, то X<\Y3 , т.е. связны графы H1 и H2 имеют хотя бы одну общую вершину. Следовательно,
связен граф H1
, т.е. связны графы H1 и H2 имеют хотя бы одну общую вершину. Следовательно,
связен граф H1 2=(G1
2=(G1 2)ЦY. Последнее означает,
что граф G1
2)ЦY. Последнее означает,
что граф G1 2
2
 2 также Цсвязен;
2 также Цсвязен; также Цсвязен;
также Цсвязен; 2). Пусть <Ø. Действительно, простой цикл, содержащий а, можно получить,
объединить два ребра
2). Пусть <Ø. Действительно, простой цикл, содержащий а, можно получить,
объединить два ребра  VG<\U. Поскольку граф G связен, то в нем найдется такое ребро
VG<\U. Поскольку граф G связен, то в нем найдется такое ребро  (рис. 5.1). Пусть SЦпростой цикл, содержащий ; но это противоречит выбору ребра
(рис. 5.1). Пусть SЦпростой цикл, содержащий ; но это противоречит выбору ребра 

 <={
<={
 5). Пусть
5). Пусть  EG. Будучи связным, граф G содержит простую цепь
EG. Будучи связным, граф G содержит простую цепь  6). Пусть a,b,c
6). Пусть a,b,c
 EG. По словию в графе имеется простая (
EG. По словию в графе имеется простая (

 ,
,  ,
,  i<} - множество ребер. Тем самым, ребра двудольного графа
i<} - множество ребер. Тем самым, ребра двудольного графа

 асодержит (с
асодержит (с
 цепь и объединение этих цепей дает простой цикл в графе G. Обозначим этот цикл через С'. Ясно, что С' содержит по крайне мере две вершины каждого из блоков B
цепь и объединение этих цепей дает простой цикл в графе G. Обозначим этот цикл через С'. Ясно, что С' содержит по крайне мере две вершины каждого из блоков B . Поэтому из тверждения
34.3 следует, что цикл С' должен содержаться в каждом их этих блоков. Последнее означает, что каждая пара блоков
B
. Поэтому из тверждения
34.3 следует, что цикл С' должен содержаться в каждом их этих блоков. Последнее означает, что каждая пара блоков
B аимеет не менее |C<'|
аимеет не менее |C<'|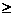 общих вершин. Получаем противоречие с тверждением 5.2. доказано.
общих вершин. Получаем противоречие с тверждением 5.2. доказано.
 k
k i
i


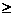 3. Пусть
3. Пусть  3.
3. 1, b
1, b p, c
p, c <', uc
<', uc , va
, va , vb
, vb . Тогда в графе Guc вершины множества
. Тогда в графе Guc вершины множества  авходят в один блок и,
следовательно, tuv<<tuc. Последнее противоречит выбору ребра uv.
авходят в один блок и,
следовательно, tuv<<tuc. Последнее противоречит выбору ребра uv. i+1
i+1 <Ø (
<Ø (
 . Поэтому
. Поэтому  <{
<{ <{
<{
 атакже не имеет точек сочленения,
что противоречита предположению.
атакже не имеет точек сочленения,
что противоречита предположению. Gx)=2 (Равенство
Gx)=2 (Равенство  Gx)=1 невозможно в силу Цсвязности графа G). Тогда в графе Gx существуют две вершины, даление которых делают его несвязным. Одной из них должна быть
Gx)=1 невозможно в силу Цсвязности графа G). Тогда в графе Gx существуют две вершины, даление которых делают его несвязным. Одной из них должна быть  (в противном случае
(в противном случае  Gx)=2). далению вершины
Gx)=2). далению вершины  аиз Gx соответствует даление вершины граф G имеет такую вершину
аиз Gx соответствует даление вершины граф G имеет такую вершину


 ). Пусть vЦпервая, считая от а, вершина Р, принадлежащая одной из Pi (i<=
). Пусть vЦпервая, считая от а, вершина Р, принадлежащая одной из Pi (i<=
 ), у которой ребро, инцидентно вершине а, не принадлежит EH. Ясно,
что такая цепь среди Pi (i<=
), у которой ребро, инцидентно вершине а, не принадлежит EH. Ясно,
что такая цепь среди Pi (i<=

 (z)=2k. Очевидно, что граф G0Цz связен, следовательно, по теореме 7.1 существует разрез G
(z)=2k. Очевидно, что граф G0Цz связен, следовательно, по теореме 7.1 существует разрез G аграфа G0 по вершине z такой, что
аграфа G0 по вершине z такой, что  T1, Е, Tn
графа G1 остовные деревья T'1, Е, T'n графа G, никакие два из этих деревьев не будут иметь общих ребер. Всего при построении этих n деревьев использовано (m1+1)+Е+(mn+1)
ребер графа G, инцидентных вершине z. В силу неравенства (1), мы получаем,
что
T1, Е, Tn
графа G1 остовные деревья T'1, Е, T'n графа G, никакие два из этих деревьев не будут иметь общих ребер. Всего при построении этих n деревьев использовано (m1+1)+Е+(mn+1)
ребер графа G, инцидентных вершине z. В силу неравенства (1), мы получаем,
что (2)
(2) остались неиспользованными еще хотя бы
остались неиспользованными еще хотя бы  а(где a
а(где a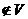 ). далим в графе G все ребра между вершинами из множеcтва А, объединим все вершины множемтва А в одну новую вершину а. Для любой вершины b
). далим в графе G все ребра между вершинами из множеcтва А, объединим все вершины множемтва А в одну новую вершину а. Для любой вершины b , мы добавим ровно dG(b, A) ребер ab. Все вершины из V<\A и соединяющие их ребра в графе GA будут же, как и в графе G. Назовем построенный граф GA стягиванием графа G по множеству А.
, мы добавим ровно dG(b, A) ребер ab. Все вершины из V<\A и соединяющие их ребра в графе GA будут же, как и в графе G. Назовем построенный граф GA стягиванием графа G по множеству А. аполучен из Н в результате замены вершины на полный грaф Kn, причем все ребра, инцидентные вершине в графе Н, в H
аполучен из Н в результате замены вершины на полный грaф Kn, причем все ребра, инцидентные вершине в графе Н, в H аопределим граф Hn, в котором каждую вершину а графа H заменим полным графом Kn (других вершин в Hn нет). Для каждого ребра ab
графа Н проведем в графе Hn ребро, соединяющее какиеЦто две вершины из соответствующих a
и b полных графов (такие ребра графа
Hn мы назовем главными). При этом, мы проведем главные ребра так,
чтобы никакие два из них не имели общего конца (это возможно так, как n>
аопределим граф Hn, в котором каждую вершину а графа H заменим полным графом Kn (других вершин в Hn нет). Для каждого ребра ab
графа Н проведем в графе Hn ребро, соединяющее какиеЦто две вершины из соответствующих a
и b полных графов (такие ребра графа
Hn мы назовем главными). При этом, мы проведем главные ребра так,
чтобы никакие два из них не имели общего конца (это возможно так, как n>