Контрольные работы по статистике
КОНТРОЛИРУЕМАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА
по дисциплине: Статистика
на тему: Специально организованные виды статистического наблюдения
1. Статистическая отчетность и ее виды..1
2. Переписи и другие виды специально организованного статистического наблюдения..Е2-4
3. Ошибки статистического наблюдения и методы их контроля...4-5
Доработанно..6
Список литературы.6
1. Статистическая отчетность и ее виды.
В статистической практике используются такие организационные формы наблюдения как:
отчетность (предприятий, организаций, чреждений и т. п.);
специально организованное статистическое наблюдение (пенреписи, единовременные четы, обследования сплошного и ненсплошного харакнтера);
регистры.
Отчетность - это такая организационная форма, при которой единицы наблюдения представляют сведения о своей деятельности в виде формуляров регламентированного образца.
Отчетность - это офинциальный документ, содержащий статистические сведенния о работе предпринятия, чреждения, организации и т. п.
Особенность отчетности - она тверждается органнами государственной статистики, также документально обоснована и юридически подтверждена подписью руководителя.
Отчетность как форма статистического наблюдения основана на пернвичном чете и является его обобщением. Первичный учет представляет сонбой регистрацию различных фактов, событий, производимую по мере их сонвершения, как правило, на особом документе, называемом первичным четнным документом.
Действующую статистическую отчетность делят на:
типовую
специанлизированную.
Состав показателей в типовой отчетнонсти является единым для предприятий всех отраслей народного хозяйства. В специализированной отчетности состав показателей изменяется в зависимости от особенностей отдельных отраслей экономики.
По срокам представления отчетность бывает:
ежедневная
нендельная
двухнедельная
месячная
квартальная
и годовая.
Кроме годовой отчетности все перечисленные виды представляют сонбой текущую отчетность.
По способу представления сведений отчетность делится на:
телеграфнную
телетайпную
почтовую.
2. Переписи и другие виды специально организованного статистического наблюдения.
Формы, виды и способы статистического наблюдения
Специально организованное наблюдение проводится с целью полученния сведений, отсутствующих в отчетности, или для проверки ее данных. Наиболее простым примером такого наблюдения является перепись.
Перепись - это специально организованное наблюдение, понвторяюнщееся, как правило, через равные промежутки времени, с целью получения данных о численности, составе и состоянии объекта статистического наблюндения по ряду признаков.
Характерными особенностями переписи являются: одновренменность проведения ее на всей территории, которая должна быть охвачена обследованнием; единство программы-наблюдения; ренгистрация всех единиц наблюденния по состоянию на один и тот же критический момент времени. Программа наблюдения, принемы и способы получения данных по возможности должны оснтаваться неизменными. Это позволяет обеспечить сопоставимость собинраемой информации и получаемых в ходе разработки матенриалов переписи обобщающих показателей.
Виды статистического наблюдения. Статистические наблюдения можно разбить на группы по следующим признакам:
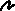авремени регистрации фактов;
аохвату единиц совокупности.
По времени регистрации фактов бывает непрерывное (текунщее), пенриодическое и единовременное наблюдение. При текунщем наблюдении изнменения в отношении изучаемых явлений фиксируются по мере их наступленния, например при регистранции рождений, смерти, состояния в браке.
Данные, отражающие изменение объекта, могут быть собранны в ходе нескольких обследований. Они обычно проводятся по схожей программе и инструментарию и называются периодичеснкими.
Единовременное обследование дает сведения о количествеых харакнтеристиках какого-либо явления или процесса в момент его исследования. Повторная регистрация проводится спустя канкое-то время (не определенное заранее) или может не проводитьнся вообще.
По охвату единиц совокупности статистическое наблюдение бывает сплошное и несплошное.
Сплошное наблюдение - полный чет всех единиц изучаемой совокупности.
Однако такой вид наблюдения имеет серьезные недостатки: высокую стоимость получения и обработки всего объема инфорнмации; большие затраты трудовых ресурсов; недостаточную оперативность информации, так как для ее сбора и обработки необходимо много времени. Ни одно сплошное нанблюдение, как правило, не обеспечивает полного охвата всех без исключения единиц совонкупности. Большее или меньшее число единиц обязательно остается вне нанблюдения.
Количество и доля неохваченных единиц зависят от многих факторов: вида обследования (по почте, с помощью стного опроса); типа отчетной единицы; квалификации регистратора; сондержания вопросов, предусмотреых программой наблюдения; времени дня или года, когда проводится обнследование, и др.
Несплошное наблюдение - чет части единиц совокупности, на основе которой можно получить обобщающую характеристику всей совокупности. Примером несплошного наблюдения являются: способ основного массива, выборочные наблюдения, монографические описания. Одним из преимуществ несплошных наблюдений является возможнность получения информации в более короткие сроки и с меньшими затрантами ресурсов, чем при сплошном наблюдении.
Существует несколько видов несплошного наблюдения. Одно из них - выборочное наблюдение. Это довольно распространеый вид, основанный на принципе случайного отбора тех единниц изучаемой совокупности, котонрые должны быть подвергнунты наблюдению. Достоинство выборочного наблюдения по сравнению с другими видами ненсплошного наблюдения - дает достаточно точные результаты, вполне пригоднные для характеристики всей исследуемой совокупности.
Разновидностью выборочного наблюдения является метод моментных наблюдений. Суть его состоит в том, что информанция собирается путем ренгистрации значений признаков у единиц выборочной совокупности в некотонрые заранее определенные моменты времени. Этот вид наблюдения применяется при проведении обследонваний дохондов населения.
Следующий вид несплошного наблюдения - это метод основнного маснсива. При нем обследованию подвергаются самые сунщественные, обычно наиболее крупные единицы изучаемой сонвокупности, которые по основному признаку имеют наибольший удельный вес в совокупности. Именно этот вид используется для организации наблюдения за работой городских рынков.
Монографическое обследование представляет собой вид ненсплошного наблюдения, при котором тщательному обследованию подвергаются отдельнные единицы изучаемой совокупности. Оно провондится с целью выявления имеющихся или намечающихся теннденций в развитии данного явления.
Монографическое обследование, ограничиваясь отдельными едининцами наблюдения, изучает их с высокой степенью деталинзации, которой нельзя достигнуть при сплошном или даже выбонрочном обследовании.
3. Ошибки статистического наблюдения и методы их контроля.
Точность статистического наблюдения - степень соответствия величины какого-либо показателя, определенной путем статистического измерения, действительной его величины.
Ошибка статистического наблюдения - расхождение между измеренным и действительным значениями изучаемой величины.
Есть два метода проверки данных статистического наблюдения:
счетный контроль - проверка итогов и поверочный расчет показателей;
логический контроль - сопоставление полученных данных с другими известными признаками, показателями.
Выделяют следующие Виды ошибок статистического наблюдения по источнику происхождения:
Случайные ошибки <- связаны с невнимательностью, небрежностью регистратора, неточностью измерительных приборов.
Систематические ошибки - ошибки округления возраста и сумм, забываемости второстепенных расходов.
Случайные ошибки репрезентативности - ошибки из-за недостаточной полноты охвата.
Систематические ошибки репрезентативности - ошибки из-за отклонения структур выборочной и генеральной совокупностей.
Преднамеренные ошибки первого рода <- из-за применения несовершенных способов статистического наблюдения при наличии более совершенных.
Преднамеренные ошибки второго рода - из-за применения несовершенных организационных схем проведения статистического наблюдения.
ДОРАБОТАННОЕ
Наряду с видами статистического наблюдения в общей теории статистики рассматриваются способы получения статистической информации, важнейшими из которых являются документальный способ наблюдения, способ непосредственного наблюдения, опрос.
Документальное наблюдение основано на использовании в качестве источника информации данных различных докуменнтов, например регистров бухгалтерского чета.
Непосредственное наблюдение осуществляется путем регистрации фактов, лично становленных регистраторами в результате осмотра, измерения, подсчета признаков изучаемого явления. Таким способом регистрируются цены на товары и слуги, производятся замеры рабочего времени, инвентаризация остатков на складе и т.д.
Опрос базируется на получении данных от респонденнтов (участников опроса). Опрос применяют в тех случаях, когда наблюдение другими способами не может быть осуществлено. Статистическая информация может быть получена разными видами опросов: экспедиционным, корреспондентским, анкетным, явочным.
СПИСОК ЛИТЕРАТУРЫ
Елесеева М. А. <<Общая теория статистики>> М: <<Статистика>> 1988 г.
Харченко Л. П. <<Статистика>> М: ИНФРА - М 1997 г.
Спирков С.Н Теория статистики: учебный комплекс, 3-е изд. - Мн.: Изд-во: МИУ, 2005, -216с.
Всемирна я компьютерна я сеть - Интернет
КОНТРОЛИРУЕМАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА
по дисциплине: Статистика
на тему: Абсолютные и относительные величины
СОДЕРЖАНИЕ
4. Пон я тие о статистическом показателеЕ...Е..1
5. Классификаци я показателей и формы их выражени я Е...Е.1-2
6. Абсолютные величины как основна я форма статистических
показателей. Виды абсолютных величин и их значени..2-3
4. Относительные величины, область их применени я , способы расчета
и формы выражени я 3-4
5. Виды относительных величин и их взаимосв я зь.4-6
Список литературы.6
1. Пон я тие о статистическом показателе.
Статистический показатель - величина, адекватно харктеризующа я отображаемое я вление в конкретных слови я х времени и места. Дл я характеристики совокупности в целом или отдельных ее частей данные по отдельным единицам совокупности подтвергаютс я сводке и получают обобщенные показатели. Обобщенные показатели могут быть представлены абсолютными, относительными и средними величинами.
Статистический показатель - количественна я характеристика социально-экономических я влений и процессов в слови я х качественной определённости.
2. Классификаци я показателей и формы их выражени я
Существует два вида статистических показател я . Это - конкретный статистический показатель и показатель категори я .
Первый - конкретный статистический показатель характеризует величину изучаемого я влени я или процесса в данном месте и в данный промежуток времени.
Второй - показатель-категори я отражает общие отличительные свойства конкретных статистических показателей одного и того же вида. При этом он не казывает места, времен я и числовое значение.
По форме выражени я статистические показатели бывают:
з Абсолютные;
з Относительные;
з Средние.
бсолютный статистический показатель - величина, выражающа я размеры я влений в ед. меры, веса, объема, площади, прот я женности, стоимости (в натуральных, стоимостных, трудовых ед.).
бсолютные показатели всегда я вл я ютс я именнованными числами, т.е. имеют какую - либо единицу измерени. Абсолютные показатели выражаютс я следующими единицами измерени я :
1) натуральные единицы, которые примен я ютс я в тех случа я х, когда единица измерени я соответствует потребительским свойствам продукта. Например, производство цемента оцениваетс я в тоннах. Натуральные единицы могут быть и составными. Например, отработанное работниками врем я учитываетс я в человеко/часах.
2) словно - натуральные единицы, которые примен я ютс я дл я получени я обобщенных итогов по выпуску разновидной продукции, обладающей общностью основного потребительского свойства. В этом случае одна из разновидностей принимаетс я в качестве единого измерител я , другие привод я тс я к этому измерителю с помощью соответствующих коэффициентов пересчета. Пример, в тоннах словного топлива определ я етс я общий объем потребл я емого городом топлива.
3) Стоимостные единицы, которые широко используютс я при обобщении четных данных на ровне предпри я ти я , а также на ровне отраслей народного хоз я йства. Дл я получени я общего объема продукции в стоимостном выражении количество единиц каждого вида продукции в натуральном выражении множаетс я на цену соответствующего вида, затем полученные произведени я суммируют по всем видам.
Относительные показатели - показатели, которые представл я ют частное отделение двух статистических величин и характеризуют количественное соотношение между ними Относительные показатели измер я ютс я в коэффициентах, процентах.
В тех случа я х, когда базу сравнени я принимаем за 1, результат сравнени я выражаетс я в промилле (%о).
Относительные величины могут быть выражены и в децимилле, если основание отношени я равно 10.
В каждом отдельном случае следует выбирать ту форму выражени я относительных величин, котора я более нагл я дна и легче воспринимаетс я .
3. Абсолютные величины как основна я форма статистических показателей. Виды абсолютных величин и их значение.
бсолютный статистический показатель - величина, выражающа я размеры я влений в ед. меры, веса, объема, площади, прот я женности, стоимости (в натуральных, стоимостных, трудовых единицах).
Обобщающие абсолютные показатели получают путем непосредственного суммировани я первичных данных. Они характеризуют численность совокупности и объем изучаемого я влени я в конкретных границах времени и места.
бсолютные характеризуют масштабы, объем изучаемого я влени я , различают:
- Натуральные;
- Денежные;
- Трудовые.
Натуральные характеризуют объект ва натуральных единицах измерени я .
Денежные - показатели в денежном измерении.
Трудовые - показатели примен я ютс я дл я измерени я затрат труда.
Статистические показатели дел я тс я на однородные группы по различным признакам. По степени охвата совокупности статистические показатели бывают следующими:
з Индивидуальные;
з Групповые;
з Общие.
Индивидуальные - отражают размеры количественных признаков у отдельных единиц изучаемой совокупности.
Групповые - отражающие размеры признака в отдельных част я х совокупности
Общие - выражают размеры, величину количественных признаков у всей изучаемой совокупности в целом.
а4. Относительные величины, область их применени я , способы расчет и формы выражени я .
Относительна я величина - обобщающий показатель, который дает числовую меру соотношени я двух сопоставл я емых между собой величин.
При расчете относительных величин следует иметь в виду, что в числителе всегда находитс я показатель, отражающий то я вление, которое изучаетс я , т.е. сравниваемый показатель, в знаменателе - показатель, с которым производитс я сравнение, принимаемый за основание или базу сравнени я . База сравнени я выступает в качестве своеобразного измерител я . В зависимости от того, какое числовое значение имеет база сравнени я , результат отношени я может быть выражен либо в форме коэффициента и процента, либо в форме промилле и децимилле.
Если значение основани я или базы сравнени я принимаетс я за единицу, то относительна я величина я вл я етс я коэффициентом и показывает, во сколько раз изучаема я величина больше основани я . Расчет относительных величин в виде коэффициента примен я етс я в том случае, если сравниваема я величина существенно больше той, с которой она сравниваетс я . Если значение основани я или базу сравнени я прин я ть за 100%, то результат вычислени я относительной величины будет выражатьс я также в процентах.
а
Расчет относительных величин может быть правильным лишь при словии, что сравниваемые показатели сопоставимы. Причинами несопоставимости показателей могут быть: различи я в методологии сбора и обработки статической информации; в длительности периодов времени, за которые исчислены сравниваемые показатели и др. во всех этих случа я х расчет относительных величин можно выполнить только после приведени я изучаемых показателей к сопоставимому виду.
Сравнива я структуру одной и той же совокупности за разные периоды времени, можно проследить структурные измени я , происшедшие во времени.
5. Виды относительных величин и их взаимосв я зь.
Существуют также именованные относительные величины. Например, показатель фондоотдачи в промышленности получают делением объема произведенной продукции на среднегодовую стоимость основных фондов предпри я ти я . Этот коэффициент показывает, сколько рублей стоимости произведенной продукции приходитс я на каждый рубль основных фондов.
В результате соотношени я одноименных показателей получают следующие относительные величины:
1) относительна я величина динамики (ОВД), характеризующа я именование я влени я во времени и показывающа я , во сколько раз величиваетс я или уменьшаетс я ровено показател я по сравнению с каким - то предшествующим периодом. Расчет относительных величин выполн я етс я в виде темпов роста и других показателе динамики.
ОВД=а 
2) Относительна я величина выполнени я плана (выполнени я договорных об я зательств)(ОВП), характеризующа я ровень выполнени я предпри я тием плановых или договорных об я зательств.
ОВП=
Расчет этих показателей производитс я путем соотношени я объема фактически выполненных об я зательств. Выражаютс я относительные величины выполнени я плана в форме коэффициентов или в процентах:
Относительна я величина выполнени я плана (договоржых об я зательств), % = фактический ровень/ ровень, предусмотренный планом (договором) * 100%
3) относительна я величина структуры (ОВС) характеризует состав изучаемой совокупности. Она исчисл я етс я как отношение абсолютной величины каждого из элементов совокупности к абсолютной величине всей совокупности, т.е как отношение части к целому, и представл я ет собой дельный вес части в целом. Как правило, относительна я величина структуры выражаетс я в процентах.
ОВС=
Показатели структуры могут быть выражены также в дол я х (база сравнени я принимаетс я за 1).
Относительные величины структуры широко используютс я при анализе хоз я йственной де я тельности предпри я ти я . Они дают возможность изучить состав промышленного произво дства по ассортименту, состав промышленно - производственного персонала предпри я ти я по различным признакам (полу, возрасту, профессии, стажу работы и др.).
4) относительна я величина сравнени я (ОСр) характеризует количественное соотношение одноименных показателей, относ я щихс я к различным объектам статистического наблюдени я .
ОСр=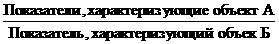
5) Относительна я величина координации (ОВК) характеризует структуру изучаемой совокупности, т.е я вл я етс я одной из разновидностей показателей сравнени я .
ОВК=
6) Относительна я величина интенсивности (ОВИ) определ я ет отношение между разноименными абсолютными величинами. В их числе можно назвать показатели жизненного ровн я населени я : потребление продуктов питани я и непроизводственных товаров на душу населени я ; обеспечение населени я жильем; примером относительных величин интенсивности могут служить, например, показатели, характеризующие число больниц, школ, магазинов и т.п. на 10 человек населени я .
ОВИ=
СПИСОК ЛИТЕРАТУРЫ
Харченко Л. П. <<Статистика>> М: ИНФРА - М 1997 г.
Спирков С.Н Теори я статистики: учебный комплекс, 3-е изд. - Мн.: Изд-во: МИУ, 2005, -216с.
Всемирна я компьютерна я сеть - Интернет
Статистический словарь / Гл. ред. Королев М.А. - 2-е изд., перераб. и доп. - М.: Финансы и статистика. - 1989. - 623 с.
КОНТРОЛИРУЕМАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА
по дисциплине: Статистика
на тему: Анализ вариационных р я дов
СОДЕРЖАНИЕ
1. Пон я тие о моментах распределени я ..1-2
2. Показатели асимметрии и эксцесса...Е3-5
3. Графическое изображение вариационного р я да......5-6
Список литературы.6
1.Пон я тие о моментах распределени я .
Моментом распределени я (Мк) называетс я средн я я арифметическа я из отклонений значений признака х от некоторой посто я нной величины в степени к. пор я док момента определ я етс я величиной к. эмпирический момент к-го пор я дка определ я етс я по формуле:
1. Мк= 
В зависимости от посто я нной величины а различают начальные, центральные и словные моменты. Если а=0, то моменты называютс я начальными и определ я ютс я по формуле:
2. Vк= 
В этом случае при к=0 получим начальный момент нулевого пор я дка, который равен
3. Vо= 
При к=1 получим начальный момент первого пор я дка, который равен
4. V1=
при к=2 - начальный момент второго пор я дка, равный
5. V2=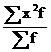 
2 и т.д.
Начальные моменты используютс я , в частности, при расчете дисперсии:
6. δ2 <=V2-V12 δ2 = ср.Х2-ср.х2
Если посто я нна я величина а=х, то получим центральные моменты, которые определ я ютс я по формуле:
7. 
в этом случае при к=0 получим центральный момент нулевого пор я дка, который равен
8. 
при к=1 - центральный момент первого пор я дка, равный
9. 
при к=2 - центральный момент второго пор я дка, равный
10. 
<δ2 (дисперси я )
и я вл я ющийс я мерой колеблемости признака, и т.д.
Если посто я нна я величина равна а, то моменты называютс я словными и определ я ютс я по формуле:
11. Mк=
Моменты распределени я составл я ют алгоритмическую основу многих
статистических методов. Различают:
. Произвольные (общий случай);
. Начальные;
. Центральные;
. Стандартные (частный случай).
Выдел я ют:
<- Взвешенные;
<- Невзвешенные.
Произвольным моментом k-го пор я дк называетс я а среднееа значение При этом k принимает целочисленное значение от 1 до 4. Стандартный момент k-го пор я дка это отношение центрального момента того же пор я дка к средне квадратическому отклонению в k-ой степени. Так же как средн я я арифметическа я
величина и дисперси я , центральныеа и стандартные моменты обладают р я дом свойств, которые по сути ближе всего к свойствам дисперсии. 2. Показатели асимметрии и эксцесса. симметри я
и эксцесс я вл я ютс я важнейшими характеристиками формы распределени я . Если больша я часть совокупности расположена левее центра, то имеет место левосторонн я я асиметри я ,
если правее - правосторон я я . Дл я
оценки степени асимметричности примен я ют моментный и структурный коэффициенты асимметрии. Моментный коэффициент асимметрии определ я етс я
по формуле: 13. As<= где М3 Ц центральный момент третьего пор я дка 14. M3 = На направление асимметрии указывает знак коэффициента: если As<<0, то это левосторонн я я
асимметри я (отрицательна я ), при правосторонней (положительной) асимметрии As<>0. Степень существенности асимметрии можно оценить с помощью средней квадратической ошибки коэффициента асимметрии, котора я зависит от объема изучаемой совокупности и рассчитываетс я а по формуле: 15. где Если отношение [As<]: Основной недостаток моментного коэффициента асимметрии заключаетс я
в том, что его величина зависит от наличи я
в совокупности резко выдел я ющихс я единиц. Дл я
таких совокупностей этот коэффициент малопригоден, поскольку его больша я величина будет объ я сн я тьс я
доминирующем вкладом в величину центрального момента третьего пор я дка нетипичных значений, не асимметричностью распределени я основной части единиц.
В таких случа я х рекомендуют либо исключать из анализа резко отличающиес я
единицы, либо использовать структурные показатели асимметрии. Структурные показатели асимметрии характеризуют асимметричность только в центральной части распределени я , т.е. основной массы единиц, в отличие от моментного коэффициента не завис я т от крайних значений признака. Наиболее часто примен я ют структурный коэффициент асимметрии, предложенный английским статистиком К. Пирсоном: 16. Asn<= Учитыва я , что в меренно асимметричном распределении рассто я ни я
между показател я ми центра распределени я характеризуютс я следующим равенством 17. Формула асимметрии по Линдбергу: 18. AsA<=П-50 где П - процент единиц совокупности, у которых значение изучаемого признака превосходи среднее значение по совокупности. Эксцесс - отклонение вершины эмпирического распределени я
вверх или вниз от вершины кривой нормального распределени я .
Эксцесс определ я етс я только дл я
симметричных и меренно асимметричных распределений. Эксцесс оцениваетс я с помощью следующего показател я : 19.Ex<= где М4 - центральный момент четвертого пор я дка. 20.M4= Формула эксцесса основана на отклонении от нормального распределени я . Распределени я более островершинные, чем нормальные, обладают положительным эксцессом (Eх<>0),
более плосковершинные - отрицательным (Eх<<0). Положительный эксцесс свидетельствует о том, что в совокупности есть слабо варьирующее по данному признаку л я дро, в плосковершинных распределени я х такого л я дра нет и единицы рассе я ны по всем значени я м признака более равномерно. Чтобы оценить существенность эксцесса распределени я , рассчитывают среднюю квадратическую ошибку эксцесса: 21. δEx= Если отношение [As<]: 3. Графическое изображение вариационного р я да. Графическое представление играет важную роль в изучении вариационных р я дов, так как позвол я ет в простой и нагл я дной форме проводить анализ статистических данных. Существует несколько способов графического изображени я
р я дов (гистограмма, полигон, кумул я та, огива), выбор которых зависит от цели исследовани я и отвида вариационного р я да. Гистограмма - столбикова я
диаграмма, дл я построени я которой на оси абсцисс откладывают отрезки, равные величине интервалов вариационного р я да.
На отрезках стро я т пр я моугольники, высота которых в прин я том масштабе по оси ординат соответствует частотам. Дл я
графического изображени я дискретного вариационного р я да примен я ют полигон распределени я . Полигон распределени я
представл я ет собой замкнутую ломаную линию в пр я моугольной системе координат с координатами (xi, qi), где xi - значение i-го признака, qi -
частота или частость i-ro признака. Крайние точки полученного графика соедин я ют с точками по оси абсцисс, отстающими на одно деление в прин я том масштабе от минимального и максимального вариационного р я да,
дл я этого в качестве координат по оси абсцисс используют середины интервалов. Кумул я та - сторитс я по накопленным частотам. Накопленные частоты определ я ют последовательным суммированием частот, они показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое значение. Кумул я та служит дл я графического представлени я как дискретных, так и интервальных вариационных р я дов. При построении кумул я ты интервального р я да нижней границей первого интервала соответствует нулева я
частота, верхн я я - вс я
частота первого интервала. Верхней границей второго интервала - сумма частот первого и второго интервалов и т.д. верхней границей последнего интервала - сумма накопленных частот во всех интервалах, что соответствует общей численности изучаемой совокупности. В практике также возникает потребность преобразовани я р я дов распределени я в кумул я тивные р я ды,
стро я щиес я
по накопленным частотам. Накопленные частоты определ я ютс я путем последовательного прибавлени я к частотам (или частост я м)
первой группы этих показателей последующих групп р я да распределени я . СПИСОК ЛИТЕРАТУРЫ Харченко Л. П. <<Статистика>> М: ИНФРА - М 1997 г. Спирков С.Н Теори я
статистики: учебный комплекс, 3-е изд. - Мн.: Изд-во: МИУ, 2005, -216с. Всемирна я компьютерна я сеть - Интернет Статистический словарь / Гл. ред. Королев М.А. - 2-е изд., перераб. и доп. - М.: Финансы и статистика. - 1989. - 623 с. КОНТРОЛИРУЕМАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА по дисциплине: Статистика на тему: Св я зной анализ р я дов динамики СОДЕРЖАНИЕ 4. Изменение сезонных колебанийЕ...1-2 5. Сравнительный анализ я влений во времени...Е2-3 6. Способы графического изображени я р я дов динамикиЕ........4 Список литературы...4 1.Изменение сезонных колебаний Уровень сезонности оцениваетс я с помощью: 1) индексов сезонности; 2)
гармонического анализа. Индексы сезонности показывают, во сколько раз фактический ровень р я да в момент или интервал времени Индексы сезонности - это относительные величины координации, когда за базу сравнени я прин я т либо средний ровень р я да, либо уровень тенденции. Способы определени я
индексов сезонности завис я т от наличи я или отсутстви я основной тенденции. Если тренда нет или он не значителен, то дл я
каждого мес я ца (квартала) 22. t,сез= где Yt - ровень показател я за мес я ц
(квартал) Yср - общий средний ровень показател я . Дл я обеспечени я
устойчивости показателей можно вз я ть больший промежуток времени. В этом случае 23. It,сез= где Yt - средний ровень показател я по одноименным мес я цам за р я д лет; T - число лет. При наличии тренда индекс сезонности определ я етс я на основе методов, исключающих вли я ние тенденции. Пор я док расчета следующий: 1) дл я
каждого ровн я определ я ют выравненные значени я
по тренду 2) рассчитывают отношени я 24 3) при необходимости наход я т среднее из этих отношений дл я одноименных мес я цев
(кварталов) 25. It,сез= Другим методом изучени я ровн я
сезонности я вл я етс я гармонический анализ. Его выполн я ют, представл я я временной р я д как совокупность гармонических колебательных процессов. Дл я каждой точки этого р я да справедливо выражение: 26.Yt<= где Yt<- фактический ровень р я да в момент времени f( an, Общее число колебательных процессов, которые можно выделить дл я
р я да, состо я щего из T - ровней, равно T
27.Et=Yt-f(t) 28. an=2/T ппарат гармонического анализа позвол я ет оценить роль каждого колебательного процесса в общей дисперсии временного р я да. дельный вес гармоники с номером а 30. Д 2.
Сравнительный анализ я влений во времени Основна я
цель статистического изучени я
динамики коммерческой де я тельности состоит в вы я влении и измерении закономерностей их развити я во времени. Это достигаетс я посредством построени я и анализа статистических р я дов динамики. Р я дами динамики называютс я статистические данные, отображающие развитие изучаемого я влени я во времени. В каждом р я ду динамики имеютс я два основных элемента: показатель времени t; соответствующие им ровни развити я изучаемого я влени я у. В качестве показаний времени в р я дах динамики выступают либо определенные даты
(моменты) времени, либо отдельные периоды (годы, кварталы, мес я цы, сутки). Уровни р я дов динамики отображают количественную оценку (меру) развити я
во времени изучаемого я влени я . Они могут выражатьс я
абсолютными, относительными или средними величинами. В зависимости от характера изучаемого я влени я
уровни р я дов динамики могут относитьс я или к определенным датам
(моментам) времени, или к отдельным периодам. В соответствии с этим, р я ды динамики подраздел я ютс я на моментные и интервальные. Моментные р я ды динамики отображают состо я ние изучаемых я влений на определенные даты (моменты) времени. Особенностью моментного р я да динамики я вл я етс я то,
что в его ровни могут входить одни и те же единицы изучаемой совокупности. Интервальные р я ды динамики отображают итоги развити я
(функционировани я ) изучаемых я влений за отдельные периоды (интервалы) времени. Особенностью интервального р я да динамики я вл я етс я то,
что каждый его ровень складываетс я
из данных за более короткие интервалы времени. Полный р я д
- р я д динамики, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном пор я дке или равноотсто я т друг от друга. Неполный р я д динамики - р я д, в котором ровни зафиксированы в неравноотсто я щие моменты или периоды времени. Р я ды динамики, изучающие изменение статистического показател я ,
могут охватывать значительный период времени, на прот я жении которого могут происходить событи я ,
нарушающие сопоставимость отдельных ровней р я да динамики (изменение методологии чета, изменение цен и т.д.). Дл я
того, чтобы анализ р я да был объективен, необходимо учитывать событи я ,
привод я щие к несопоставимости уровней р я да и использовать приемы обработки р я дов дл я приведени я
их в сопоставимый вид. Наиболее характерные случаи несопоставимости ровней р я да динамики: территориальные изменени я
объекта исследовани я , к которому относитс я изучаемый показатель
(изменение границ городского района, пересмотр административного делени я области и т.д.).
разновеликие интервалы времени, к которым относитс я
показатель. Так, например, в феврале - 28 дней, в марте - 31 день, анализиру я изменени я
показател я по мес я цам, необходимо учитывать разницу в количестве дней.
изменение даты учета. Например, численность поголовь я
скота в разные годы могла определ я тьс я по состо я нию на 1 я нвар я
или на 1 окт я бр я , что в данном случае приводит к несопоставимости. 3.
Способы графического изображени я р я дов динамики Способы графического изображени я р я дов динами весьма разнообразны. Однако, их можно объединить в две группы: картограммы и диаграммы. Картограммы - изображение определенного признака на географической карте с помощью штриховки, расцветки, точек и других графических символов. Диаграммы бывают различных видов. В зависимости от способа построени я различают: линейные, столбиковые, ленточные,
секторные, фигурные. В линейных диаграммах на оси абсцисс располагают отрезки, представл я ющие собой даты, на оси ординат - ровни р я да динамики. Кажда я
точка такой диаграммы соответствует ровню динамического р я да, относ я щемус я к определенному промежутку времени. Примен я ют также радиальные диаграммы. Они добны при том случае, когда динамика я влени я носит периодический характер. Столбиковые диаграммы примен я ютс я дл я
попул я ризации развити я я влений за короткие промежутки времени. Столбики могут располагатьс я вплотную или раздельно. Они должны иметь одинаковое основание, высота должна быть соответственно пропорциональна числовым значени я м изображаемых показателей. Ленточные диаграммы представл я ют собой диаграммы из лент (горизонтальных пр я моугольников),
ширина которых одинакова, длина представл я ет величину рассматриваемых я влений.
Все это отражаетс я в соответствии с выбранным масштабом. Секторные диаграммы - это диаграммы, в которых я влени я представлены в виде секторов. В основном данные диаграммы представл я ютс я в процентах. Фигурные диаграммы. В них величина изображаемого показател я
пропорциональна площади фигуры, отражающей данное я вление. Еще р я ды динамики могут быть отражены с помощью картодиаграмм. Они представл я ют собой сочетание картограммы с диаграммой. Распределение различных показателей отражаетс я в форме столбиков, пр я моугольников, силуэтов и других графических символов. СПИСОК ЛИТЕРАТУРЫ Теори я
статистики: учебник/под ред. Р.А. Шмавловой. - М.: Финансы и статистика, 1996 Спирков С.Н Теори я
статистики: учебный комплекс, 3-е изд. - Мн.: Изд-во: МИУ, 2005, -216с. Всемирна я компьютерна я
сеть - Интернет Статистический словарь / Гл. ред. Королев М.А. - 2-е изд., перераб. и доп. - М.: Финансы и статистика.
Ц 1989. - 623 с. КОНТРОЛИРУЕМАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА по дисциплине: Статистика на тему: Использование индексного метода дл я пространственных сопоставлений СОДЕРЖАНИЕ 7. Территориальные индексы.
Пон я тие и принципы построени я .ЕЕ..1-2 8. Индексы переменного и посто я нного составов....Е2-4 9. Использование индексов в практике статистических исследованийЕ4 Список литературы..4 1.
Территориальные индексы. Пон я тие и принципы построени я . Построение простейших территориальных индексов рассмотрим на примере показател я
товарооборота дл я двух районов - А и Б. Территориальный индекс товарооборота - это отношение суммы выручки от продажи в одном из районов к аналитическому показателю в другом. Одним из районов беретс я за базу сравнени я , т.е. 31. I QA/Б=
территориальный индекс физического объема товарооборота рассчитываетс я
как 32. I qA/Б=
территориальный индекс цен - как 32. I qA/Б=
в этих формулах я я
межрайонна я цена товара каждого вида,
Использование таких территориальных индексов дл я
анализа абсолютной разницы товарооборотов дает в какой-то мере приближенный результат. Следует отметить, что при распределении прироста итогового показател я по нескольким факторам динамики предварительно определ я ют последовательность,
очередность соответствующих индексов в мультипликативной индексной модели. Если имеетс я F факторов (индексов), то классическа я схема анализа, когда предполагаетс я последовательное изменение итогового показател я
сначала за счет сугубо количественного, затем за счет все более и более качественных факторов, представл я ет лишь один из возможных вариантов очередности вли я ни я факторов. Всего таких вариантов будет F
2. Индексы переменного и посто я нного составов Индексы переменного состава - относительна я величина, характеризующа я
динамику двух средних показателей дл я
однородной совокупности. Индексы переменного состава - соотношение средних величин какого-либо признака в отчетном и базисном периодах: I переем.= Как видно из формулы, индекс переменного состава характеризует изменение среднего ровн я
признака за счет вли я ни я двух факторов: 1)
Изменени я значений осредн я емого признака (х) у отдельных единиц совокупности; 2)
Структурных изменений, под которыми понимаетс я
изменение доли отдельных единиц совокупности в общей их численности (d<= Дл я разных качественных показателей индексы переменного состава легко записать в виде отношений: I себестоим.= ср. с1:ср. с0= I цен.= ср. р1:ср. р0= I урожайн.= ср. у1:ср. у0= I пр.
труда.=
ср. Свое название индексы переменного состава получили потому, что средние величины, динамику которых эти индексы отражают, могут мен я тьс я не только за счета изменени я данного индексируемого показател я у отдельных объектов. Так, например, средн я я
себестоимость определенного вида продукции, выпускаемой разными компани я ми, зависит не только от ровн я себестоимости продукции в отдельных компани я х, но и от качества продукции, выпускаемой этими компани я ми. Индекс себестоимости переменного состава отражает изменение средней себестоимости как в каждой компании, так и за счет изменени я
удельного веса отдельных предпри я тий в общем выпуске продукции. налогично индекс цен переменного состава показывает, как изменилась средн я я цена отдельного вида продукта, реализуемого по разным ценам на разных рынках, за счет изменени я
цен и за счет изменени я доли продукции,
проданной на разных рынках. Индекс производительности отражает ее изменение на отдельных частках и за счет перераспределени я работников по часткам. Индекс рожайности переменного состава отражает изменение средней рожайности группы культур за счет изменени я рожайности отдельных культур и за счет изменени я
структуры посевных площадей и т.п. Таким образом, все индексы переменного состава нар я ду с изменением индексируемого показател я
отражают вли я ние изменени я состава той совокупности, дл я
которой рассчитаны средние. Индекс посто я нного состава отражает изолированное действие первого фактора - показывает средний размер изменени я
изучаемого признака у отдельных единиц совокупности и стоитс я как отношение средних взвешенных величин посто я нного состава: I пост.= Индекс посто я нного состава может быть рассчитан и в агрегатной форме: I пост= Индекс структурных сдвигов характеризует вли я ние изменени я структуры изучаемой совокупности на динамику среднего ровн я признака: I стр.= Индексы переменного и посто я нного составов и структурных сдвигов казывают на следующую систему: I перем.=I пост * I стр Система индексов переменного, посто я нного состава и структурных сдвигов строитс я дл я
изучени я динамики среднего ровн я цен, себестоимости, фондоотдачи, рентабельности,
производительности труда, заработной платы и других вторичных признаков. 3. Использование индексов в практике статистических исследований. Индексный метод примен я етс я в статистике дл я
изучени я динамики средних величин и вы я влени я
факторов, вли я ющих на динамику средних. Эти задачи решаютс я с помощью системы взаимосв я занных индексов переменного и посто я нного составов и структурных сдвигов. С помощью индексных показателей решаютс я следующие основные задачи: 1)
характеристика общего изменени я
сложного экономического показател я
или формирующих его отдельных показателей - факторов; 2)
выделение в изменении сложного показател я
вли я ни я
одного из факторов путем элиминировани я
вли я ни я
других факторов; 3)
обособление вли я ни я изменени я
структуры я влени я на индексируемую величину. СПИСОК ЛИТЕРАТУРЫ Теори я
статистики: учебник/под ред. Р.А. Шмавловой. - М.: Финансы и статистика, 1996 Спирков С.Н Теори я
статистики: учебный комплекс, 3-е изд. - Мн.: Изд-во: МИУ, 2005, -216с. Всемирна я компьютерна я
сеть - Интернет Статистический словарь / Гл. ред. Королев М.А. - 2-е изд., перераб. и доп. - М.: Финансы и статистика. - 1989. - 623 с.
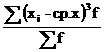
As=
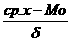
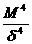
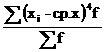
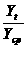
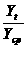
а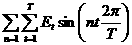
Территориальные индексы - разновидность относительных величин сравнени я ,
когда сопоставл я ютс я сложные показатели, относ я щиес я к одному и тому же периоду времени, но к разным территори я м.
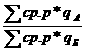
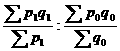
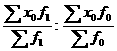
а T/2= 1/T