О квази генетическом коде
Творческая группа юных математиков - программистов, руководимая Братом Михаилом Шишигиным.
(Церковь Христа Спасителя)
О КВАЗИ ГЕНЕТИЧЕСКОМ КОДЕ
Аннотация
Приводится класс полимино, моделирующий фундаментальное свойство генетического кода, именно то, что 20 различных аминокислот, входящих в структуру белков, образованы из 4 различны нуклеотидов. Этот класс полимино назван квазигенетическим кодом.
Вводятся нарные операции < <-, <-1, * > над матрицами 4*2
 |
 |
|
a1 |
a2 |
||
|
|
b2 |
||
|
c1 |
c2 |
||
|
d1 |
d2 |
состоящими из элементов 0, 1, 2, 3, именно:
|
|
|
|
|
|
a2 |
a1 |
|
|
|
4 - a2 | 4 - a1 |
|
|
|
|
|
2 - d1 | 2 - d2 | ||||||||||
|
|
|
|
|
|
b2 |
b1 |
|
|
|
4 - b2 | 4 - b1 |
|
|
|
|
|
2 - c1 |
|
||||||||||
|
|
|
|
|
|
c2 |
c1 |
|
= |
|
4 - c2 | 4 - c1 |
, |
|
|
|
|
2 - b1 | 2 - b2 | ||||||||||
|
|
|
|
|
|
d2 |
d1 |
|
|
|
4 - d2 | 4 - d1 |
|
|
|
|
|
2 - a1 | 2 - a2 | ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
2 |
|
|
|
d1 |
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
2 |
|
|
|
c1 |
c2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
2 |
|
|
|
b1 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
2 |
|
|
|
a1 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a,
 W* =а (W)-1,
W* =а (W)-1,
 |


 W = W, (W-1) = (W)-1.
W = W, (W-1) = (W)-1.
Используя введенные операции над матрицами 4*2, элементы квазигенетического кода можно записать так:
3 1
3 2
3 1 2 1 2 0 1 3 0 1 0 1 2 1 1 1 0 2 1
3 1
3 1
0 1 3 1 3 1 3 1 3 1 1 3 1 3 1 3 3 1 Положим, что прямоугольник размерома 4*2а должен быть покрыт прямоугольниками размерома 2*1 (домино). Причём, нечётное число домино должно выходить за пределы как стороны
AB, так и стороны CDа (рис.
1). Покрытие, в котором домино, выходящие за пределы сторона
AB и CD, однозначно определяют структуру покрытия прямоугольника ABCD, назовём жестким покрытием. Например, покрытие
Рис. 2 Прямоугольник размерома 4*2n аразобьём вертикалями на а Будем считать, что клетка прямоугольник ABCDа находится в состоянии 0, 1, 2, 3, если она покрыта домино,
ориентированным соответственно вверх, вправо, вниз, влево. 0 3 1 2 Матрицу размерома 4*2 , соответствующую жесткому покрытию прямоугольника ABCD будем называть квазинуклеотидной матрицей, либо квазинуклеотидом. Матрицу размером 4*2n , соответствующую квазигенетическому покрытию прямоугольника размером 4*2n , будем называть белковой матрицей. Методом последовательного исключения (перебором) можно показать, что существуют 20 различных, жестких покрытий прямоугольника ABCD.
в Таблице 1 приведены все 20 жестких покрытий прямоугольник 4*2 и соответствующие им квазинуклеотидные матрицы.
3 1 3 2 3 1 2 1 2 0 1 3 0 1 0 1 2 1 1 3 1 3 0 1
b<= 2 1 1 0 2 1 3 0 1 1 3 3
b*<= 1 3
d-1= 1 3 3 2 3 1 2 0 2 1 0 1 0 1 1 3
b-1= 1 3
g-1= 2 1
a-1= 2 1 2 1 0 1 0 1 0 2 1 3 3 1 3 0 3 1 3 1 3 2 3 1 a = 3 2 d = 3 0 3 1 3 0 3 1 3 1 1 3 1 3 1 3 l = 3 1 3 1 3 2 1 3
3 1 g*= 3 0 3 2 1 3 1 3 3 0 3 1 3 1 3 1
1 3
3 1 3 1 l-1 <= 1 3 1 3 1 3
a*= 3 2
d*= 3 1 3 1 3 0 3 2 3 1 3 1 3 0 3 1 Пусть записи
a, b Î { 0, 1, 2, 3}. Введём нарные операции < <-, <-1, * > над матрицейа
4*2





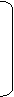

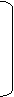
а
а

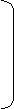 3
3
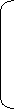
 3
3
 1
1
а
d =
О КВАЗИГЕНЕТИЧЕСКОМ КОДЕ
B
C
A
D
Рис. 1
B
C
B
C
B
C
A
D
A
D
A
D
a)
b)
c)
Рис. 3
Таблице 1
a<=
b<=
g =

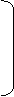


2

d =
0
3
1
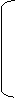

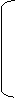

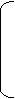
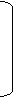

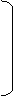
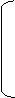
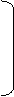



l =



а

а
а




|
a1 |
a2 |
||
|
|
b2 |
||
|
c1 |
c2 |
||
|
d1 |
d2 |
,
состоящей из элементов 0, 1, 2, 3.
Положим
|
|
|
|
|
|
a2 |
a1 |
|
|
|
4 - a2 | 4 - a1 |
|
|
|
|
|
2 - d1 | 2 - d2 | ||||||||||
|
|
|
|
|
|
b2 |
b1 |
|
|
|
4 - b2 | 4 - b1 |
|
|
|
|
|
2 - c1 |
|
||||||||||
|
|
|
|
|
|
c2 |
c1 |
|
= |
|
4 - c2 | 4 - c1 |
, |
|
|
|
|
2 - b1 | 2 - b2 | ||||||||||
|
|
|
|
|
|
d2 |
d1 |
|
|
|
4 - d2 | 4 - d1 |
|
|
|
|
|
2 - a1 | 2 - a2 | ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
2 |
|
|
|
d1 |
d2 |
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
2 |
|
|
|
c1 |
c2 |
|
, |

|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
2 |
|
|
|
b1 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
2 |
|
|
|
a1 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 +а |
2
+а |
|
2 +а |
2 +а |
|
2 +а |
2 +а |
Положим
|
 W* =а (W)-1,
W* =а (W)-1,
 |
|||
 |
|||
 Нетрудно показать, что W = W, (W-1) = (W)-1, (W-1)-1 =а W.
Нетрудно показать, что W = W, (W-1) = (W)-1, (W-1)-1 =а W.
Используя введенные операции над матрицами 4*2, квазинуклеотидные матрицы можно записать така (см. Таблицу 1) :
Введём понятие генетической информации белковой матрицы. Последовательность из количества единичных элементов в правых столбцах квазинуклеотидных подматриц белковой матрицы будем называть генетической информацией. Например, на рис. 4
показано квазигенетическое покрытие прямоугольника размером 4´22, которому соответствует белковая матрица с генетической информацией 1 3 3 1 3 3 1 3 3 1 3. 2 1 1 3 3 2 2 1 3 1 3 1 3 1 3 1 3 1 3 1 0 2 2 1 3 1 3 0 0 1 3 1 3 2 1 3 1 3 1 3 2 1 3 0 1 3 3 1 3 1 3 1 3 0 2 1 3 1 3 2 0 1 1 3 1 3 1 3 1 3 1 3 1 3 1 3 0 1 3 1 3 0 2 3 Используя жёсткость паковки квазигенетического покрытия, можно показать, что квазигенетическийа код обладает высокой помехоустойчивостью. Предложение
1. По двум любым строкам квазигенетического покрытия прямоугольника, размером 4´2 Предложение 2. Зная жёсткие покрытия на нечётных шагах квазигенетического покрытия прямоугольника размером, 4´2(2 Дальнейшие исследования должны показать плодотворность идеи квазигенетического кода. Приложение. 2 1 1 3 3 2 2 1 3 1 3 1 3 1 3 1 3 1 3 1 0 2 2 1 3 1 3 0 0 1 3 1 3 2 1 3 1 3 1 3 2 1 3 0 1 3 3 1 3 1 3 1 3 0 2 1 3 1 3 2 0 1 1 3 1 3 1 3 1 3 1 3 1 3 1 3 0 1 3 1 3 0 2 3 2 1 1 3 3 2 2 1 3 1 3 1 3 1 3 1 3 1 3 1 0 2 2 1 3 1 3 0 0 1 3 1 3 2 1 3 1 3 1 3 2 1 3 0 1 3 3 1 3 1 3 1 3 0 2 1 3 1 3 2 0 1 1 3 1 3 1 3 1 3 1 3 1 3 1 3 0 1 3 1 3 0 2 3 2 1 1 3 3 2 2 1 3 1 3 1 3 1 3 1 3 1 3 1 0 2 2 1 3 1 3 0 0 1 3 1 3 2 1 3 1 3 1 3 2 1 3 0 1 3 3 1 3 1 3 1 3 0 2 1 3 1 3 2 0 1 1 3 1 3 1 3 1 3 1 3 1 3 1 3 0 1 3 1 3 0 2 3 2 1 1 3 3 2 2 1 3 1 3 1 3 1 3 1 3 1 3 1 0 2 2 1 3 1 3 0 0 1 3 1 3 2 1 3 1 3 1 3 2 1 3 0 1 3 3 1 3 1 3 1 3 0 2 1 3 1 3 2 0 1 1 3 1 3 1 3 1 3 1 3 1 3 1 3 0 1 3 1 3 0 2 3



1
2
3
4
5
6
7
8
9
10
11
1
3
3
1
3
3
1
3
3
1
3
3
1
0
1




b
a
l
d
d
l
a
g
t-1
g
a
Рис. 4
3
1
0
1
3
1
0
1
3
1
0
1
3
1
0
1



 а2 +а d2
а2 +а d2 d1
d1