Исследование регрессии на основе численных данных

Федеральное агентство по образованию

Государственное образовательное

учреждение высшего профессионального образования

Новгородский Государственный ниверситет

Имени Ярослава Мудрого.

Кафедр Прикладная математик и информатика.

Курсовая работ по дисциплине

Математическая статистика

на тему:

Исследование регрессии на основе численных данных

Преподаватель:

Токмачев М.С.

Студента группы <№ 3311

Jannat

Новгорода Великий

2005

ПЛАН

Теоретическая часть

1. Понятие регрессии

2. INDEX e " " z "1049" Постоянная и случайная составляющие случайной переменой

3. Модель парной линейной регрессии

4. Регрессия по методу наименьших квадратов

5. Качество оценки: коэффициент R<²

6. Точность коэффициентов регрессии

7. Доверительные интервалы

8. F<-статистика

Практическая часть

I. Исследование регрессии при выборке из генеральной совокупности N(0;1)

II. Исследование регрессии при выборке из генеральной совокупности N(0;0,5)

. Исследование регрессии при выборке из генеральной совокупности N(0;2)

Заключение

Условное математическое ожидание M(Y<|X<=x) случайной переменной Y, рассматриваемое как функция x, т.е. M(Y<|X<=x)=f(x), называется функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно также условное математическое ожидание M(X<|Y<=y), случайной переменной X, т.е. M(X<|Y<=y)=f(x), называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).

Функции регрессии выражают математическое ожидание переменной Y (или X) для случая, когда другая переменная принимает определённое числовое значение, или, иначе говоря, функция M(Y<|X<=x) показывает, каково будет в среднем значение случайной переменной Y, если переменная X принимает значение x. Всё сказанное справедливо и для функции M(X<|Y<=y).

Становится очевидным, что функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией словного распределения.

Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X,Y). Только зная вид этого распределения, можно точно определить вид функции регрессии, затем оценить его параметры. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объёма, по которой нужно найти вид двумерного распределения (X,Y), затем вид функции регрессии. Это может привести к значительным ошибкам, т.к. одну и ту же совокупность точек (x_i,y_i) на плоскости можно одинаково спешно описать с помощью различных функций.

Для характеристики формы связи при изучении корреляционной зависимости пользуются понятием кривой регрессии. Кривой регрессии Y по X (или Y по X) называется словное среднее значение случайной переменной Y (Х), рассматриваемой как функция от x (у). Эта функция обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза.

2. Постоянная и случайная составляющие случайной переменой

Часто вместо рассмотрения случайной величины как единого целого можно и добно разбить ее на постоянную и чисто случайную составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если x случайная переменная и m - ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом:

x<= m<+u,

где u чисто случайная составляющая (в регрессионном анализе она обычно представлена случайным членом)

3. Модель парной линейной регрессии

Коэффициент корреляции показывает, что две переменные связаны друг с другом, однако не дает представления о том, каким образом они связаны.

Рассмотрим простейшую модель: y<=a<+

Величина yа рассматривается как зависимая переменная, состоящая из:

На графиках подбора в проделанной работе мы видим Y предсказанное (■) и Y полученное. На них показано, как комбинация этих двух составляющих определяет величину Y. Показатели Xi Ца это гипотетические значения объясняющей переменной. Если бы соотношение между Y и X было точным, то соответствующие значения Y были бы представлены Y предсказанное (■). Наличие случайного члена приводит к тому, что в действительности значение Y получается другим.

Задача регрессионного анализа состоит в получении оценок

Очевидно, что чем меньше значения u, тем легче эта задача. Действительно, если бы случайный член отсутствовал вовсе, то точки Y совпадали бы с точками Y предсказанное и точно бы показали положение прямой. В этом случаю было бы достаточно просто построить эту прямую и определить значения a и b.

Почему существует случайный член:

1. Невключение объясняющих переменных. Соотношение между X и Y почти всегда является очень большим прощением. В действительности существуют другие факторы влияющие на Y, которые не чтены в формуле y<=a<+

2. Агрегирование переменных. во многих случаях рассматриваемая зависимость - это попытка объединить вместе некоторое число соотношений. Так как отдельные соотношения, вероятно, имеют разные параметры, любая попытка определить соотношение между ними является лишь аппроксимацией. Наблюдаемое расхождение при этом приписывается наличию случайного члена.

3. Неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Иногда может показаться, что существует зависимость между Y и X, но это будет лишь аппроксимация, и расхождение вновь будет связано с наличием случайного члена.

4. Неправильная функциональная спецификация. Функциональное соотношение между Y и X математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, быть более сложной. Безусловно, надо постараться избежать возникновения этой проблемы, используя подходящую математическую формулу, но любая самая изощренная формула является лишь приближением, и существующее расхождение вносит вклад в остаточный член.

5. Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить вклад в остаточный член.

Остаточный член является суммарным проявлением всех этих факторов. Очевидно, что если бы вас интересовало только измерение влияния X на Y, то было бы значительно добнее, если бы остаточного члена не было. Если бы он отсутствовал, мы бы знали, что любое изменение Y от наблюдения к наблюдению вызвано изменением X, и смогли бы точно вычислить b. Однако в действительности каждое изменение Y отчасти вызвано изменением u, и это значительно сложняет жизнь.

5. Регрессия по методу наименьших квадратов

Пусть мы имеем наблюдения X и Y, то перед нами стоит задача - определить значения a и b. В качестве грубой аппроксимации можно это сделать на глаз, построив прямую, в наибольшей степени соответствующую этим точкам. Отрезок, отсекаемый прямой на оси OY, представляет собой оценку a, гловой коэффициент прямой представляет собой оценку b.

Необходимо признать, что мы никогда не сможем рассчитать истинные значения a и b при попытке построить прямую и определить положение линии регрессии. Мы можем получить только оценки, и они могут быть хорошими или плохими. Иногда оценки могут быть абсолютно точными, но это возможно лишь в результате случайного совпадения, и даже в том случае не будет способа знать, что оценки абсолютно точны.

Первым шагом является определение остатка для каждого наблюдения. Разность между фактическим и расчетным значениями, то есть Y и Y предсказанное, описывается как остаток. Обозначим остаток какого-то наблюдения за

Стандартный же остаток (отклонение)- мера разброса для распределения вероятностей, это квадратный корень из дисперсии.

Очевидно, что мы хотим построить линию регрессии таким образом, чтобы эти остатки были минимальными. Необходимо выбрать какой-то критерий подбора, который будет одновременно учитывать величину всех остатков. Один из способов решения поставленной проблемы состоит в минимизации суммы квадратов остатков

S<=<å

В соответствии с этим критерием, чем меньше S, тем строже соответствие.

Существуют и другие достаточно разумные решения, однако при выполнении определенных условий метод наименьших квадратов дает несмещенные и эффективные оценки a и b.

6. Качество оценки: коэффициент R<²

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной Y. Мы пытаемся сделать это путем определения регрессионной зависимости Y от соответственно выбранной независимой переменной X. Но мы не можем с помощью уравнения регрессии объяснить расхождение между фактическим и расчетным значениями Y. Коэффициент детерминации R<² - та часть дисперсии Y, которая объяснена уравнением регрессии.

R<²=D(Y расчетное)

D(Y)

Максимальное значение коэффициента R<² равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что Y<=Yрасчетному для всех наблюдений и все остатки равны нулю.

Если в выборке отсутствует видимая связь между X и Y, то R<² будет близок к нулю. При прочих равных словиях желательно, чтоб коэффициент R<² был как можно больше.

7. Точность коэффициентов регрессии

Увеличивая u, мы величиваем его стандартное отклонение, следовательно, величиваем стандартные отклонения a и b. Чем больше число наблюдений, тем меньше дисперсии оценок. Чем большей информацией мы располагаем, тем более точными будут наши оценки. Чем больше дисперсия X, тем меньше будут дисперсия коэффициентов регрессии.

Коэффициенты регрессии вычисляются на основании предположения, что наблюдаемые изменения Y происходят вследствие изменений Х, но в действительности они лишь отчасти вызваны изменением Х, а отчасти вариациями u. Чем меньше дисперсия Х, тем больше, вероятно, будет относительное влияние фактора случайности при определении отклонений Y и тем более вероятно, что регрессионный анализ может оказаться неверным. Важные значения имеют дисперсия случайного члена и дисперсия Х.

Дисперсия случайного члена нам неизвестна, но мы можем получить ее оценку на основе остатков. Разброс остатков относительно линии регрессии будет отражать неизвестный разброс u относительно линии y<=a<+

Рассматривая теоретические дисперсии оценок a и b и оценку случайного члена, можно получить оценки теоретических дисперсий для a и b и после извлеченного квадратного корня - оценки их стандартных отклонений. Вместо термина лоценка стандартного отклонения функции плотности вероятности коэффициента регрессии будем использовать термин стандартная ошибка коэффициента регрессии.

Стандартная ошибка дает только общую оценку степени точности коэффициентов регрессии. Она позволяет получить некоторое представление о кривой функции плотности вероятности. Однако она не несет информации о том, находится ли полученная оценка в середине распределения и, следовательно, является точной или в лхвосте распределения и, таким образом, относительно неточна.

Чем больше дисперсия случайного члена, тем, очевидно, больше будет выборочная дисперсия остатков и, следовательно, существеннее стандартные ошибки коэффициентов в уравнении регрессии, что позволяет с высокой вероятностью заключить, что полученные коэффициенты неточны. Однако это всего лишь вероятность. Возможно, что в какой-то конкретной выборке воздействия случайного фактора в различных наблюдениях будут взаимно погашены и в конечном итоге коэффициенты регрессии будут точны. Проблема состоит в том, что, вообще говоря, нельзя тверждать, произойдет это или нет.

8. Доверительные интервалы

Вопрос стоит в том, насколько сильно гипотетическое значение может отличаться от результата эксперимента, прежде чем они станут несовместимыми. Гипотетическое значение β является совместимым с результатом оценивания регрессии (b), если оно довлетворяет двойному неравенству:

b<-с.о.(b)*tкрит << β < b<+с.о.(b)* tкрит

Любое гипотетическое значение β, которое довлетворяет этому соотношению, будет автоматически совместимо с оценкой b, иными словами, не будет опровергаться ею. Множество этих значений, определенных как интервал между нижней и верхней границами неравенства, известно как доверительный интервал для величины β.

9. F<-статистика

F<-статистика используется для проверки качества оценивания регрессии и записывается как отношение объясненной суммы квадратов (в расчете на одну независимую переменную к остаточной сумме квадратов) в расчете на одну степень свободы

SS - сумма квадратов отклонений (с.к.о.)

Df - число степеней свободы (с.с.)

MS - с.к.о. деленная на с.с.

F<-статистика - MS регрессии деленная на MS остатка

Задание

Необходимо исследовать регрессию на основе численных данных. Задана истинная зависимость:а

Вариант №10

y<=4+3x, x<∈[5,20]

Практическая часть

Задана истинная зависимость

1. На промежутке [5;20] выберем 30 значений, равноудаленных от соседних, таким образом, составим выборку для X. Вычислим для этой выборки значения Y:

X	Y
5	19
5,40	20,20
5,81	21,44
6,62	23,85
6,77	24,32
6,87	24,61
6,94	24,81
7,02	25,06
8,12	28,35
8,13	28,38
9,44	32,32
9,46	32,39
10,12	34,36
10,42	35,27
10,89	36,67
11,02	37,06
12,19	40,58
12,46	41,38
12,53	41,60
12,63	41,88
13,28	43,83
13,93	45,80
14,62	47,86
14,94	48,82
15,39	50,18
18,08	58,23
18,14	58,42
19,38	62,14
19,50	62,51
19,88	63,64
19,99	63,96
20	64

2. Используя генератор случайных чисел, находим по 30 значений Ui, Vi.Выборку производим из нормальной генеральной совокупности N(0;1).

Ui	Vi
0,17465	-0,13918
0,608766	2,200486
0,256966	0,415696
-0,40546	-0,77361
-0,50702	1,026156
0,148453	-0,27599
0,69341	1,812241
0,355941	0,428406
-1,70596	0,488922
0,638124	0,200499
-0,79704	0,109958
0,717844	0,516177
0,676484	0,522041
0,481091	-2,68454
-0,66089	0,171234
0,69098	0,560749
-1,05002	-0,11743
-0,77062	-1,04935
1,754124	0,002257
-0,70798	-1,37519
-0,62831	-1,6882
-1,99856	0,206826
-0,05951	0,11504
0,656803	1,57218
-1,15063	-0,32191
0,580	-0,62645
-0,36795	-0,29376
0,839377	-1,40617
-1,53361	-1,85625
-1,88214	2,009965

3. Полагая вместо Xi значения X<+Ui, вместо Yi - Y<+Vi, получим две зависимые выборки:

Xi	Yi
5,17465	18,86082
6,142534	22,80179
6,686606	23,70461
6,102919	22,75152
6,323632	25,51811
7,310079	25,20889
8,52568	29,30905
8,407487	28,58304
6,451793	28,96217
9,030714	29,37827
7,730137	29,69149
9,914749	32,10689
12,50058	39,99431
12,54094	37,495
11,43878	40,47025
13,59	43,0214
11,84024	42,55334
12,57741	42,99474
17,06511	49,93521
15,34643	50,78805
15,49843	50,69203
14,13871	52,61864
16,1716	52,80839
17,39148	55,7762
16,84934	57,678
19,04975	58,78113
18,18456	59,36377
19,80434	59,48872
17,69916	59,84204
18,11786	66,00997

4. По полученным значениям находим равнение линейной регрессии (Excel<àАнализ данныхàРегрессия)

y = 2,959989002*x<+ 4,977076691

также:

коэффициент детерминации R²а 0,957421057

доверительные интервалы для коэффициентов

Y:(1,816620984; 8,137532399)

X:(2,718346233; 3,20163177)

стандартные ошибки коэффициентов Y: 1,542882806 X: 0,117966049

F<-статистика: 629,6020401

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	20,29398457	-1,433162272	-0,492864465
2	23,15894	-0,357118898	-0,122813179
3	24,76935672	-1,064742069	-0,366164768
4	23,04164954	-0,290126919	-0,099774639
5	23,69495855	1,82315541	0,626983094
6	26,61483142	-1,40594406	-0,483504123
7	30,21299691	-0,903945143	-0,310866709
8	29,86314499	-1,280101594	-0,440226902
9	24,07431234	4,887859798	1,680934847
10	31,70789177	-2,329613	-0,801157014
11	27,85819572	1,833292384	0,630469199
12	34,32462506	-2,217731899	-0,762677938
13	41,97864341	-1,984328613	-0,682410554
14	42,09811424	-4,60373	-1,583009803
15	38,83574651	1,634507824	0,562107195
16	44,97006519	-1,94866985	-0,670147507
17	40,02405468	2,529284508	0,869820871
18	42,20607611	0,788668616	0,271223115
19	55,48960825	-5,554400732	-1,910158256
20	50,40235334	0,385771	0,132642243
21	50,85227346	-0,160247411	-0,05510908
22	46,82750936	5,791126	1,991570588
23	52,84484634	-0,036456609	-0,012537427
24	56,45565155	-0,679455491	-0,233664724
25	54,85093911	2,827058233	0,975247
26	61,36411843	-2,582990043	-0,290203
27	58,80317324	0,560592623	0,192787787
28	63,59771108	-4,10899113	-1,413081934
29	57,36638532	2,475657295	0,851378474
30	58,60572907	7,404236032	2,546316563

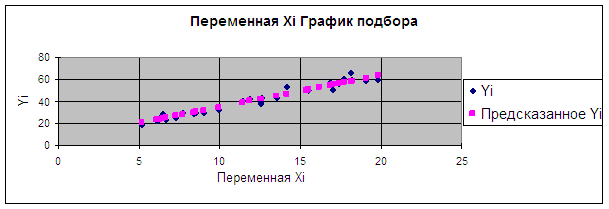
5. Сравним равнение полученной регрессии с истинной зависимостью:

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,040011. При этом константа изменяется по сравнению с заданной приблизительно на 0,9771.

6. Изменяя только Yi(Yi = Y + Vi) и оставляя неизменными X, получим пару выборок:

X	Yi
5,00	18,86082
5,53	22,80179
6,43	23,70461
6,51	22,75152
6,83	25,51811
7,16	25,20889
7,83	29,30905
8,05	28,58304
8,16	28,96217
8,39	29,37827
8,53	29,69149
9,20	32,10689
11,82	39,99431
12,06	37,495
12,10	40,47025
12,82	43,0214
12,89	42,55334
13,35	42,99474
15,31	49,93521
16,05	50,78805
16,13	50,69203
16,14	52,61864
16,23	52,80839
16,73	55,7762
18,00	57,678
18,47	58,78113
18,55	59,36377
18,96	59,48872
19,23	59,84204
20,00	66,00997

Теперь находим равнение линейной регрессии:

коэффициент детерминации R²: 0,994191219

доверительные интервалы для коэффициентов:

Y: (3,750717832; 6,051396589)

X : (2,840155626; 3,013361321)

стандартные ошибки коэффициентов: Y: 0,561576877а X: 0,042278094

F<-статистика: 4792,288613.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,53484958	-0,674029578	-0,627575517
2	21,09706173	1,704728266	1,58723854
3	23,71905932	-0,019322	-0,013453476
4	23,94950571	-1,197985713	-1,115420639
5	24,89272815	0,625381854	0,58228059
6	25,86140687	-0,652516867	-0,60754546
7	27,8242206	1,484829404	1,382495088
8	28,465987	0,117053004	0,108985721
9	28,77682166	0,185348338	0,172574147
10	29,46414142	-0,085871418	-0,079953167
11	29,85804397	-0,166553968	-0,155075083
12	31,81817809	0,288711912	0,268813912
13	39,50731665	0,486993352	0,453429812
14	40,19731601	-2,702316014	-2,516072624
15	40,31387901	0,156370987	0,145593912
16	42,42273144	0,598668557	0,557408371
17	42,62772155	-0,074381545	-0,069255176
18	43,96752614	-0,972786139	-0,905741801
19	49,71260823	0,601766	0,207260071
20	51,45089	-1,100400893	-1,024561358
21	52,10014002	-1,408110019	-1,311063197
22	52,13092	0,487684475	0,454073303
23	52,40561547	0,402774534	0,375015347
24	53,87940052	1,896799481	1,766073
25	57,58262041	0,095379586	0,006033
26	58,95592012	-0,174790122	-0,162743602
27	59,19976456	0,164005442	0,152702201
28	60,4069285	-0,918208496	-0,854925645
29	61,19071418	-1,348674183	-1,255723674
30	63,43622668	2,573743318	2,396361149

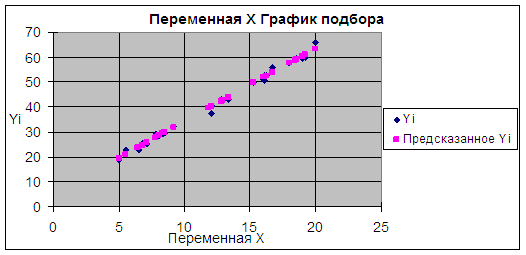
Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,0732. При этом константа изменяется по сравнению с заданной приблизительно на 0,901.

Сравним полученное равнение с первоначальным равнением y<=a<+

y = 2,959989002x<+ 4,977076691

Коэфициент при переменной X отличается от коэффициента в первоначальном равнении регрессии приблизительно на 0,03323. При этом константа изменяется по сравнению с первоначальным значением в равнении регрессии примерно на 0,07602.

7. Полагая вместо Vi значение 0,5Vi;1,5Vi и так далее получим новые пары выборок и вновь вычислим равнение линейной регрессии.

Vi<=0,5Vi:

Ui	Vi=0,5Vi
0,17	-0,07
0,61	1,10
0,26	0,21
-0,41	-0,39
-0,51	0,51
0,15	-0,14
0,69	0,91
0,36	0,21
-1,71	0,24
0,64	0,10
-0,80	0,05
0,72	0,26
0,68	0,26
0,48	-1,34
-0,66	0,09
0,69	0,28
-1,05	-0,06
-0,77	-0,52
1,75	0,00
-0,71	-0,69
-0,63	-0,84
-2,00	0,10
-0,06	0,06
0,66	0,79
-1,15	-0,16
0,58	-0,31
-0,37	-0,15
0,84	-0,70
-1,53	-0,93
-1,88	1,00

Yi = Y<+0,5Vi:

X	Yi=Y+0.5Vi
5	18,93
5,53	21,70
6,43	23,50
6,51	23,14
6,83	25,01
7,16	25,35
7,83	28,40
8,05	28,37
8,16	28,72
8,39	29,28
8,53	29,64
9,20	31,85
11,82	39,73
12,06	38,84
12,10	40,38
12,82	42,74
12,89	42,61
13,35	43,52
15,31	49,93
16,05	51,48
16,13	51,54
16,14	52,52
16,23	52,75
16,73	54,99
18,00	57,84
18,47	59,09
18,55	59,51
18,96	60,19
19,23	60,77
20	65,00

Уравнение регрессии:

коэффициент детерминации R²: 0,998577228

доверительные интервалы для коэффициентов:

Y: (3,875361588; 5,025759)

X : (2,920077692; 3,006680471).

стандартные ошибки коэффициентов:а Y: 0,280788217 X: 0,02113903

F<-статистика: 19651,66.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,26742623	-0,337015081	-0,627576556
2	20,84918532	0,852363896	1,58723935
3	23,50399025	-0,007223556	-0,013451428
4	23,73732006	-0,598992754	-1,115421329
5	24,69232	0,312691749	0,58228258
6	25,67314358	-0,326260858	-0,607550454
7	27,66051671	0,742414584	1,38249596
8	28,31031311	0,058527233	0,108987168
9	28,62503705	0,092674288	0,172574504
10	29,32095678	-0,042936843	-0,079955343
11	29,71978798	-0,083278825	-0,155078633
12	31,70797	0,144356749	0,2688156
13	39,48979567	0,243498692	0,453433925
14	40,18842855	-1,351156818	-2,516072395
15	40,30645002	0,078187321	0,145597429
16	42,44168914	0,299331721	0,557404048
17	42,64924415	-0,037191397	-0,069256393
18	44,00581284	-0,486390854	-0,90573839
19	49,82277938	0,299801	0,20725822
20	52,02584693	-0,550198466	-1,024558478
21	52,24018478	-0,704056702	-1,311067383
22	52,27138586	0,243843866	0,454076694
23	52,54948244	0,201387433	0,375015952
24	54,041708	0,948398152	1,766070657
25	57,79126385	0,04768904	0,004702
26	59,18174676	-0,087395219	-0,162744024
27	59,42864226	0,082001316	0,152699706
28	60,65091065	-0,459103548	-0,854925016
29	61,50	-0,674335017	-1,255720801
30	63,71811245	1,286870097	2,396360129

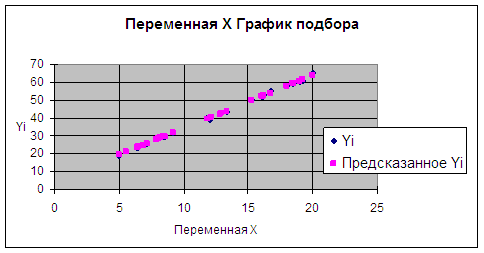
Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,0366. При этом константа изменяется по сравнению с заданной приблизительно на 0, 4505.

Vi<=1,5Vi:

Ui	Vi=1,5Vi
0,17	-0,21
0,61	3,30
0,26	0,62
-0,41	-1,16
-0,51	1,54
0,15	-0,41
0,69	2,72
0,36	0,64
-1,71	0,73
0,64	0,30
-0,80	0,16
0,72	0,77
0,68	0,78
0,48	-4,03
-0,66	0,26
0,69	0,84
-1,05	-0,18
-0,77	-1,57
1,75	0,00
-0,71	-2,06
-0,63	-2,53
-2,00	0,31
-0,06	0,17
0,66	2,36
-1,15	-0,48
0,58	-0,94
-0,37	-0,44
0,84	-2,11
-1,53	-2,78
-1,88	3,01

Yi = Y<+1,5Vi:

X	Yi=Y+1,5Vi
5	18,79
5,53	23,90
6,43	23,91
6,51	22,36
6,83	26,03
7,16	25,07
7,83	30,22
8,05	28,80
8,16	29,21
8,39	29,48
8,53	29,75
9,20	32,36
11,82	40,26
12,06	36,15
12,10	40,56
12,82	43,30
12,89	42,49
13,35	42,47
15,31	49,94
16,05	50,10
16,13	49,85
16,14	52,72
16,23	52,87
16,73	56,56
18,00	57,52
18,47	58,47
18,55	59,22
18,96	58,79
19,23	58,91
20	67,01

Уравнение регрессии

коэффициент детерминации R²: 0,986697969

доверительные интервалы для коэффициентов:

Y: (3,626084764; 7,077100176)

X : (2,760233076; 3,020041413).

стандартные ошибки коэффициентов:а Y: 0,842364652 X: 0,063417091

F<-статистика: 2076,941658.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,80227869	-1,011045244	-0,627576556
2	21,34494358	2,557091687	1,58723935
3	23,93413328	-0,021670667	-0,013451428
4	24,1616962	-1,796978261	-1,115421329
5	25,09311651	0,938075248	0,58228258
6	26,04967458	-0,978782574	-0,607550454
7	27,98792849	2,227243752	1,38249596
8	28,62166475	0,175581699	0,108987168
9	28,92861008	0,278022864	0,172574504
10	29,60732971	-0,12881053	-0,079955343
11	29,99630354	-0,249836474	-0,155078633
12	31,93191137	0,433070246	0,2688156
13	39,52483915	0,730496077	0,453433925
14	40,20620486	-4,053470453	-2,516072395
15	40,32130936	0,234561962	0,145597429
16	42,40377466	0,897995163	0,557404048
17	42,60619981	-0,574191	-0,069256393
18	43,92924002	-1,459172561	-0,90573839
19	49,60243646	0,899403	0,20725822
20	51,75105376	-1,650595399	-1,024558478
21	51,96009412	-2,112170106	-1,311067383
22	51,99052404	0,731531599	0,454076694
23	52,26174729	0,604162298	0,375015952
24	53,71709152	2,845194455	1,766070657
25	57,37397467	0,143067121	0,004702
26	58,73009089	-0,262185657	-0,162744024
27	58,97088421	0,246003949	0,152699706
28	60,16294344	-1,377310645	-0,854925016
29	60,93692196	-2,023005051	-1,255720801
30	63,15433736	3,86061029	2,396360129

Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,1099. При этом константа изменяется по сравнению с заданной приблизительно на 1,3516.

II.

1. Используя генератор случайных чисел, находим по 30 значений Ui, Vi.Выборку производим из генеральной совокупности N(0;0,5).

Ui	Vi
-0,33978	-0,62199
-0,52754	0,214371
0,561159	0,842674
-0,21023	-0,19153
0,55	-0,12142
-0,07485	0,748012
0,536907	0,02968
0,428237	1,299704
1,147537	-1,0117
-1,22736	0,118428
0,457453	0,003653
0,031557	0,213658
-0,34181	0,270182
-0,3208	0,658724
-0,63071	-0,56332
-0,49658	-0,59886
-0,97769	-0,28392
-0,06608	0,134859
-0,3185	-0,96067
0,230928	-0,01689
-0,86298	0,443846
-0,86812	0,141694
-0,01716	0,289101
-0,47807	0,589177
0,03681	-0,04456
-0,03	-0,06998
-0,0324	1,050125
-0,16564	-0,09764
-0,26828	1,051867
-0,20672	-0,92324

2. Затем, полагая вместо Xi значения X<+Ui, вместо Yi Ч Y<+Vi, получим две зависимые выборки и найдем по полученным значениям равнение линейной регрессии.

Xi	Yi
4,660218	18,37801
5,006231	20,81568
6,990799	24,13159
6,29815	23,61
7,383983	24,37054
7,08678	26,23289
8,369177	27,52649
8,479782	29,45434
9,305287	27,46155
7,165227	29,2962
8,98463	29,58518
9,228463	31,80437
11,48228	39,74246
11,73905	40,83826
11,46897	39,7357
12,32363	41,86179
11,91257	42,38685
13,28196	44,17896
14,99248	48,97228
16,28534	52,14635
15,26376	52,82408
15,26916	52,55351
16,21396	52,98245
16,2566	54,79319
18,03678	57,95535
18,24716	59,3376
18,52011	60,70765
18,79933	60,79726
18,96448	62,75016
19,79328	63,07676

y<= 3,057386713*x<+ 3,849828606

коэффициент детерминации R²: 0,987296367

доверительные интервалы для коэффициентов:

Y: (2,091385142; 5,608272069)

X : (2,923132377; 3,191641049).

стандартные ошибки коэффициентов:а Y: 0,85844335а X: 0,065540772

F<-статистика: 2176,094.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	18,09791688	0,280098	0,172302263
2	19,15581308	1,659863858	1,021082118
3	25,22340441	-1,091811	-0,671638972
4	23,10570844	0,227897612	0,140193532
5	26,42551873	-2,054980175	-1,264141935
6	25,51685652	0,716033201	0,440475099
7	29,43763863	-1,948164	-1,175662212
8	29,77580289	-0,321461291	-0,19775018
9	32,29968921	-4,838142402	-2,976232458
10	25,75669845	3,539499448	2,17735905
11	31,31931647	-1,734133513	-1,066769851
12	32,06480759	-0,260432822	-0,160207897
13	38,95560729	0,786848535	0,484037871
14	39,74063661	1,097628052	0,675217049
15	38,91489336	0,820807581	0,504928123
16	41,52793536	0,849687	0,205371027
17	40,27115213	2,115696656	1,301492295
18	44,45790793	-0,27894995	-0,171598896
19	49,68764901	-0,715365598	-0,440064416
20	53,64041694	-1,494063885	-0,91908858
21	50,51704631	2,307029716	1,419192771
22	50,53354027	2,019970659	1,242605475
23	53,42216985	-0,439718748	-0,270497456
24	53,55254369	1,240650031	0,763198473
25	58,99523708	-1,039890467	-0,639699187
26	59,63846367	-0,30086436	-0,185079768
27	60,47295567	0,234690934	0,144372513
28	61,32664816	-0,529390439	-0,325659907
29	61,83159061	0,918570407	0,565067919
30	64,36553236	-1,288776345	-0,792803864

Новое равнение регрессии сравним с первоначальным :

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,0574 При этом константа изменяется по сравнению с заданной приблизительно на 0,8498.

3. Изменяя только Yi(Yi = Y + Vi) и оставляя неизменными X, получим пару выборок, снова найдем равнение линейной регрессии.

X	Yi
5,00	18,37801
5,53	20,81568
6,43	24,13159
6,51	23,61
6,83	24,37054
7,16	26,23289
7,83	27,52649
8,05	29,45434
8,16	27,46155
8,39	29,2962
8,53	29,58518
9,20	31,80437
11,82	39,74246
12,06	40,83826
12,10	39,7357
12,82	41,86179
12,89	42,38685
13,35	44,17896
15,31	48,97228
16,05	52,14635
16,13	52,82408
16,14	52,55351
16,23	52,98245
16,73	54,79319
18,00	57,95535
18,47	59,3376
18,55	60,70765
18,96	60,79726
19,23	62,75016
20,00	63,07676

y<= 3,00165434*x<+4,06592825

коэффициент детерминации R²: 0,998303894

доверительные интервалы для коэффициентов:

Y: (3,429737572; 4,702118928)

X : (2,953758975; 3,049549705).

стандартные ошибки коэффициентов: Y: 0,310577 X: 0,023381734

F<-статистика: 16480,40672.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,07415	-0,69618995	-1,172069792
2	20,67638918	0,139290823	0,234502905
3	23,36548379	0,766106211	1,289233
4	23,60182731	-0,268217311	-0,451556947
5	24,56918684	-0,198646845	-0,334431667
6	25,56265409	0,670235907	1,128374893
7	27,5756963	-0,049206303	-0,082841216
8	28,23388553	1,220454469	2,054694721
9	28,55267447	-1,091124469	-1,836961348
10	29,25758276	0,038617235	0,065014002
11	29,6615653	-0,076385297	-0,12859838
12	31,67185933	0,132510672	0,223088191
13	39,55776325	0,184696749	0,310946
14	40,26541973	0,572840272	0,964404583
15	40,38496558	-0,649265579	-1,093070321
16	42,54778363	-0,685993627	-1,154903784
17	42,75801943	-0,371169434	-0,624881876
18	44,13210968	0,046850319	0,078874801
19	50,02420866	-1,051928657	-1,770973284
20	52,25573122	-0,109381217	-0,184148622
21	52,47283748	0,351242524	0,591949
22	52,50155	0,049068449	0,082609131
23	52,78613005	0,196319948	0,330514224
24	54,29762932	0,495560677	0,83430061
25	58,09561476	-0,140264763	-0,236142581
26	59,50405727	-0,166457266	-0,280238939
27	59,75414169	0,953508309	1,605277821
28	60,992197	-0,194937002	-0,328185967
29	61,7960398	0,954120203	1,606307974
30	64,09901505	-1,055049	-1,721016316

Новое равнение регрессии сравним с первоначальным :

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,0659. При этом константа изменяется по сравнению с заданной приблизительно на 0,0659.

4.Полагая вместо Vi значения 0,5Vi; 1,5Vi и так далее, получим новые пары выборок и вновь вычислим равнение линейной регрессии.

Vi<=0,5Vi:

Ui	0,5Vi
-0,33978	-0,31099
-0,52754	0,107185
0,561159	0,421337
-0,21023	-0,09576
0,55	-0,06071
-0,07485	0,374006
0,536907	0,01484
0,428237	0,649852
1,147537	-0,50585
-1,22736	0,059214
0,457453	0,001826
0,031557	0,106829
-0,34181	0,135091
-0,3208	0,329362
-0,63071	-0,28166
-0,49658	-0,29943
-0,97769	-0,14196
-0,06608	0,067429
-0,3185	-0,48033
0,230928	-0,00845
-0,86298	0,221923
-0,86812	0,070847
-0,01716	0,144551
-0,47807	0,294589
0,03681	-0,08
-0,03	-0,03499
-0,0324	0,525063
-0,16564	-0,04882
-0,26828	0,525934
-0,20672	-0,46162

Yi = Y<+0,5Vi

Xi	Yi=Y+0,5Vi
5,00	18,689005
5,53	20,708492
6,43	23,710256
6,51	23,429369
6,83	24,431248
7,16	25,854
7,83	27,511651
8,05	28,804489
8,16	27,967399
8,39	29,236984
8,53	29,583357
9,20	31,697546
11,82	39,607365
12,06	40,508903
12,10	40,017361
12,82	42,161216
12,89	42,528808
13,35	44,529
15,31	49,452617
16,05	52,154798
16,13	52,602153
16,14	52,482664
16,23	52,837901
16,73	54,498605
18,00	57,977628
18,47	59,372587
18,55	60,182584
18,96	60,846076
19,23	62,224228
20,00	63,538378

Уравнение регрессии:

коэффициент детерминации R²: 0,575198

доверительные интервалы для коэффициентов:

Y: (3,714868492; 4,35105)

X : (2,976879431; 3,024774857).

стандартные ошибки коэффициентов:а Y: 0,155289144 X: 0,011690882

F<-статистика: 65885,12884.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,03706	-0,348094853	-1,172067872
2	20,63884766	0,069643907	0,234497538
3	23,32720121	0,383054584	1,289780551
4	23,5634796	-0,134110577	-0,451562835
5	24,53057255	-0,099324083	-0,334433461
6	25,52376602	0,335117885	1,128373208
7	27,53625347	-0,024602829	-0,082840023
8	28,19426132	0,610228125	2,054695076
9	28,5129624	-0,545563733	-1,83696403
10	29,21767644	0,019307668	0,06501072
11	29,62154764	-0,038191065	-0,128592882
12	31,63128768	0,066257842	0,223096339
13	39,5150184	0,092346476	0,310939206
14	40,47986	0,286422667	0,964411862
15	40,34199277	-0,324632122	-1,0930
16	42,50421479	-0,342072	-1,154909902
17	42,71439266	-0,185585103	-0,624882371
18	44,08810423	0,023424382	0,078872082
19	49,97857946	-0,52596234	-1,770964307
20	52,20948706	-0,05468878	-0,18414223
21	52,42653349	0,17561958	0,591327524
22	52,45812886	0,02453499	0,082611604
23	52,73973973	0,098160829	0,330516676
24	54,25082246	0,24778252	0,83430688
25	58,04776125	-0,070133723	-0,236146792
26	59,45581562	-0,083228615	-0,280238517
27	59,70583112	0,476752824	1,605271274
28	60,94354525	-0,097469263	-0,328188108
29	61,74716652	0,477060994	1,606308911
30	64,04950712	-0,529115	-1,721019454

Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,827. При этом константа изменяется по сравнению с заданной приблизительно на 0,03296.

Vi<=1,5Vi:

Ui	1,5Vi
-0,33978	-0,93298
-0,52754	0,321556
0,561159	1,264011
-0,21023	-0,28729
0,55	-0,18213
-0,07485	1,122017
0,536907	0,044519
0,428237	1,949556
1,147537	-1,51756
-1,22736	0,177641
0,457453	0,005479
0,031557	0,320488
-0,34181	0,405273
-0,3208	0,988086
-0,63071	-0,84498
-0,49658	-0,89829
-0,97769	-0,42588
-0,06608	0,202288
-0,3185	-1,441
0,230928	-0,02534
-0,86298	0,665769
-0,86812	0,212541
-0,01716	0,433652
-0,47807	0,883766
0,03681	-0,06684
-0,03	-0,10496
-0,0324	1,575188
-0,16564	-0,14645
-0,26828	1,577801
-0,20672	-1,38487

Yi=Y+1,5Vi

Xi	Yi=Y+1,5Vi
5,00	18,0670153
5,53	20,9228623
6,43	24,5529299
6,51	23,2378431
6,83	24,3098286
7,16	26,6068955
7,83	27,5413303
8,05	30,1041938
8,16	26,955695
8,39	29,3554117
8,53	29,5870093
9,20	31,911204
11,82	39,8775468
12,06	41,1676268
12,10	39,4540412
12,82	41,5623544
12,89	42,24489
13,35	44,2463874
15,31	48,4919497
16,05	52,1379078
16,13	53,045
16,14	52,624358
16,23	53,1270016
16,73	55,0877825
18,00	57,9330657
18,47	59,3026116
18,55	61,2327093
18,96	60,7484395
19,23	63,2760945
20,00	62,615134

Уравнение регрессии:

коэффициент детерминации R²: 0,996193916

доверительные интервалы для коэффициентов:

Y: (3,144605477; 5,053179969)

X : (2,930638292; 3,074324572).

стандартные ошибки коэффициентов:а Y: 0,465867432 X: 0,035072646

F<-статистика: 7328,643424.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,29988	-1,044284559	-1,172067872
2	20,71393059	0,208931721	0,234497538
3	23,40376617	1,149163752	1,289780551
4	23,64017481	-0,402331732	-0,451562835
5	24,6078009	-0,297972248	-0,334433461
6	25,60154189	1,005353654	1,128373208
7	27,61513878	-0,073808488	-0,082840023
8	28,27350937	1,830684376	2,054695076
9	28,59238615	-1,6366912	-1,83696403
10	29,29748868	0,057923004	0,06501072
11	29,70158253	-0,114573195	-0,128592882
12	31,71243049	0,198773525	0,223096339
13	39,60050734	0,277039427	0,310939206
14	40,3083588	0,859268	0,964411862
15	40,4279376	-0,973896367	-1,0930
16	42,5913516	-1,028997217	-1,154909902
17	42,80164534	-0,55675531	-0,624882371
18	44,17611421	0,070273147	0,078872082
19	50,06983672	-1,577887019	-1,770964307
20	52,30197417	-0,164066341	-0,18414223
21	52,51914025	0,52685874	0,591327524
22	52,55075303	0,073604971	0,082611604
23	52,83251915	0,294482486	0,330516676
24	54,33491	0,74334756	0,83430688
25	58,14346687	-0,210401168	-0,236146792
26	59,55229746	-0,249685844	-0,280238517
27	59,80245079	1,430258473	1,605271274
28	61,04084725	-0,292407788	-0,328188108
29	61,84491154	1,431182983	1,606308911
30	64,14852136	-1,587345	-1,721019454

Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4 а

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,002481. При этом константа изменяется по сравнению с заданной приблизительно на 0,09889.

1. Используя генератор случайных чисел, находим по 30 значений Ui, Vi.Выборку производим из генеральной совокупности N(0;2).

Ui	Vi
0,902655	0,260757
-0,88288	-0,70846
1,771532	4,823814
-0,53499	-1,62389
2,901897	2,311372
2,35671	0,011551
1,067474	-0,01354
0,907062	-2,41
-0,19715	-0,81773
-0,28407	-0,54451
0,74835	0,729
0,36609	-1,62836
1,247126	0,04246
-1,05005	-1,07188
-0,84576	-1,06307
2,296219	-0,49956
-1,30035	0,838904
1,616459	3,673795
0,573948	2,270094
4,074464	3,471778
0,477646	-3,86124
-0,18024	-2,20909
0,706505	-0,10294
-0,10416	-2,30452
-1,4826	0,484101
0,352875	-2,26195
-3,49128	1,007611
2,101	6,252667
-2,38327	-2,36716
0,274958	-3,21194

Xi	Yi
5,902655	19,26076
4,65089	19,89285
8,201172	28,11273
5,973383	21,90124
9,73255	26,80
9,518336	25,49643
8,899744	27,48327
8,958608	25,67693
7,960601	27,62
8,108516	28,63326
9,275527	30,30598
9,562995	29,96235
13,07122	39,51473
11,0098	39,10766
11,25392	39,23596
15,11643	41,96109
11,58991	43,50967
14,96449	47,71789
15,88493	52,20305
20,12	55,63502
16,60439	48,51899
15,95703	50,20273
16,93762	52,59041
16,63051	51,89949
16,51737	58,48401
18,82207	57,14562
15,06123	60,66513
21,08717	67,14756
16,8495	59,33113
20,27496	60,78806

y<= 2,950504846*x<+ 3,41182941

коэффициент детерминации R²: 0,913294175

доверительные интервалы для коэффициентов:

Y: -1,379711969; 8,203370788)

X : (2,598577611; 3,302432082).

стандартные ошибки коэффициентов:а Y: 2,339152164 X: 0,171805123

F<-статистика: 294,9310157.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	20,82764248	-1,566882483	-0,368909635
2	17,13430405	2,758545951	0,649477029
3	27,6094258	0,503304197	0,118498847
4	21,03632487	0,864915133	0,203637177
5	32,12776609	-5,324436093	-1,253594828
6	31,49572585	-5,295854	-1,412485026
7	29,67056781	-2,187297813	-0,514981338
8	29,84425	-4,167319	-0,981160023
9	26,89962207	0,755897926	0,17796997
10	27,33604592	1,297214077	0,30541842
11	30,77931726	-0,477257	-0,443377
12	31,62749318	-1,665143183	-0,392044311
13	41,97852067	-2,463790673	-0,580079316
14	35,89629408	3,211365921	0,756089779
15	36,61656352	2,619396482	0,616715428
16	48,01294391	-6,051853913	-1,42485939
17	37,60790814	5,90176186	1,389521446
18	47,56463457	0,153255431	0,036082735
19	50,28039711	1,922652886	0,45267286
20	62,80218152	-7,16716152	-1,687449422
21	52,40316117	-3,884171169	-0,914496259
22	50,49311961	-0,290389614	-0,068369854
23	53,386363	-0,795952998	-0,187400608
24	52,48023625	-0,580746247	-0,136731943
25	52,14639722	6,337612783	1,492138973
26	58,94642758	-1,800807582	-0,423985382
27	47,85006088	12,81506912	3,017202965
28	65,62961502	1,517944977	0,3573877
29	53,12635335	6,204776646	1,460863794
30	63,23319254	-2,445132541	-0,575686411

Новое равнение регрессии сравним с первоначальным :

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,0495. При этом константа изменяется по сравнению с заданной приблизительно на 0,5882.

X	Yi
5,00	19,26076
5,53	19,89285
6,43	28,11273
6,51	21,90124
6,83	26,80
7,16	25,49643
7,83	27,48327
8,05	25,67693
8,16	27,62
8,39	28,63326
8,53	30,30598
9,20	29,96235
11,82	39,51473
12,06	39,10766
12,10	39,23596
12,82	41,96109
12,89	43,50967
13,35	47,71789
15,31	52,20305
16,05	55,63502
16,13	48,51899
16,14	50,20273
16,23	52,59041
16,73	51,89949
18,00	58,48401
18,47	57,14562
18,55	60,66513
18,96	67,14756
19,23	59,33113
20,00	60,78806

y<= 2,963989827*x<+ 4,427294273

коэффициент детерминации R²: 0,973208572

доверительные интервалы для коэффициентов:

Y: (1,898559719; 6,956028827)

X : (2,773615042; 3,154364613).

стандартные ошибки коэффициентов: Y: 1,234486867 X: 0,092937858

F<-статистика: 1017,110415.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,24724341	0,01351659	0,005725019
2	20,8293285	-0,936478498	-0,396650121
3	23,48468057	4,628049429	1,96024
4	23,71805847	-1,816818474	-0,769522493
5	24,67327966	2,130050341	0,902193407
6	25,65428096	-0,157850962	-0,066858559
7	27,64206368	-0,158793684	-0,067257854
8	28,29199401	-2,615064008	-1,107623355
9	28,60678281	-0,951262807	-0,402912089
10	29,30284597	-0,669585972	-0,283606466
11	29,70175936	0,604220635	0,255920653
12	31,68682839	-1,72447839	-0,730411392
13	39,47378064	0,040949362	0,017344306
14	40,1725575	-1,064897499	-0,451042627
15	40,2906033	-1,054643299	-0,44669941
16	42,42628248	-0,465192483	-0,197034588
17	42,63388027	0,875789731	0,370945093
18	43,99072854	3,727161457	1,578657756
19	49,80889394	2,394156056	1,014056695
20	52,01241554	3,622604458	1,53437212
21	52,22679757	-3,70780757	-1,570460321
22	52,25800508	-2,05527508	-0,870521973
23	52,53615898	0,054251024	0,022978291
24	54,02869208	-2,129202078	-0,901834121
25	57,77902071	0,704989291	0,298601718
26	59,16979019	-2,02417019	-0,857347343
27	59,41673658	1,248393424	0,528763238
28	60,63925687	6,508303129	2,756624132
29	61,43301311	-2,101883112	-0,890263037
30	63,70709082	-2,91903082	-1,236379

Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,036. При этом константа изменяется по сравнению с заданной приблизительно на 0,4273.

Vi<=0,5Vi:

Ui	0,5Vi
0,902655	0,130379
-0,88288	-0,35423
1,771532	2,411907
-0,53499	-0,81195
2,901897	1,155686
2,35671	0,005776
1,067474	-0,00677
0,907062	-1,23886
-0,19715	-0,40887
-0,28407	-0,27226
0,74835	0,365
0,36609	-0,81418
1,247126	0,02123
-1,05005	-0,53594
-0,84576	-0,53154
2,296219	-0,24978
-1,30035	0,419452
1,616459	1,836898
0,573948	1,135047
4,074464	1,735889
0,477646	-1,93062
-0,18024	-1,10455
0,706505	-0,05147
-0,10416	-1,15226
-1,4826	0,242051
0,352875	-1,13098
-3,49128	0,503806
2,101	3,126334
-2,38327	-1,18358
0,274958	-1,60597

Yi = Y<+0,5Vi

X	Y
5	19,130379
5,53	20,247076
6,43	25,700826
6,51	22,713187
6,83	25,647644
7,16	25,490654
7,83	27,490041
8,05	26,915782
8,16	28,064386
8,39	28,905515
8,53	29,943755
9,20	30,776536
11,82	39,493504
12,06	39,6436
12,10	39,767485
12,82	42,210866
12,89	43,090218
13,35	45,880997
15,31	51,067998
16,05	53,899133
16,13	50,44961
16,14	51,307272
16,23	52,64188
16,73	53,051756
18,00	58,241959
18,47	58,2766
18,55	60,161327
18,96	64,021228
19,23	60,514714
20	62,39403

Уравнение регрессии:

коэффициент детерминации R²: 0,993246535

доверительные интервалы для коэффициентов:

Y: (2,949279007; 5,478013793)

X : (2,886807583; 3,077182386).

стандартные ошибки коэффициентов:а Y: 0,61724349 X: 0,046468933

F<-статистика: 4118,019632.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,12362132	0,006757177	0,005724072
2	20,715317	-0,468240808	-0,396651406
3	23,38679937	2,31402636	1,960234548
4	23,62159496	-0,908407965	-0,769521345
5	24,58261876	1,065025609	0,902193696
6	25,56957929	-0,078925712	-0,066858749
7	27,56943707	-0,079396252	-0,067257348
8	28,22331548	-1,307533194	-1,107624262
9	28,54001651	-0,475630982	-0,402911695
10	29,240308	-0,334792685	-0,283606185
11	29,64164465	0,302110049	0,255920402
12	31,63877224	-0,862235975	-0,730408597
13	39,47302739	0,020476547	0,017345885
14	40,17604906	-0,532448672	-0,45104252
15	40,29481195	-0,527326592	-0,446703556
16	42,4434646	-0,232598	-0,197036247
17	42,65232347	0,437894849	0,370945044
18	44,0174141	1,863582642	1,578659233
19	49,87092274	1,197075097	1,014054119
20	52,08782993	1,811302582	1,534372278
21	52,30351425	-1,853904136	-1,570460474
22	52,33491133	-1,027639563	-0,870523607
23	52,61475491	0,027125107	0,022977946
24	54,11635461	-1,06459837	-0,901831
25	57,88946512	0,352493829	0,298600
26	59,28868301	-1,01208332	-0,85734576
27	59,53712951	0,624197278	0,528763669
28	60,76707617	3,254151584	2,756623895
29	61,56565419	-1,050940174	-0,890261784
30	63,85354609	-1,45951609	-1,236370472

Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4 а

Коэффициент при переменной X отклоняется от истинного значения приблизительно на 0,01801. При этом константа изменяется по сравнению с заданной приблизительно на 0, 21365.

Vi<=1,5Vi:

Ui	1,5Vi
0,902655	0,391136
-0,88288	-1,06269
1,771532	7,235721
-0,53499	-2,43584
2,901897	3,467058
2,35671	0,017327
1,067474	-0,02031
0,907062	-3,71657
-0,19715	-1,2266
-0,28407	-0,81677
0,74835	1,086674
0,36609	-2,44254
1,247126	0,06369
-1,05005	-1,60782
-0,84576	-1,59461
2,296219	-0,74934
-1,30035	1,258356
1,616459	5,510693
0,573948	3,405141
4,074464	5,207667
0,477646	-5,79186
-0,18024	-3,31364
0,706505	-0,15441
-0,10416	-3,45678
-1,4826	0,726152
0,352875	-3,39293
-3,49128	1,511417
2,101	9,379001
-2,38327	-3,55074
0,274958	-4,81791

Yi=Y+1,5Vi

X	Y
5	19,391136
5,53	19,538616
6,43	30,52464
6,51	21,089297
6,83	27,959016
7,16	25,502205
7,83	27,476501
8,05	24,438072
8,16	27,246656
8,39	28,361005
8,53	30,668204
9,20	29,148176
11,82	39,535964
12,06	38,57172
12,10	38,704415
12,82	41,711306
12,89	43,929122
13,35	49,554792
15,31	53,338092
16,05	57,370911
16,13	46,58837
16,14	49,098182
16,23	52,53894
16,73	50,747236
18,00	58,72606
18,47	56,01465
18,55	61,168938
18,96	70,273895
19,23	58,147554
20	59,18209

Уравнение регрессии:

коэффициент детерминации R²: 0,940679

доверительные интервалы для коэффициентов:

Y: (0,84783702; 8,43404138)

X : (2,660422749; 3,231547158).

стандартные ошибки коэффициентов:а Y: 1,851730471 X: 0,1394068

F<-статистика: 446,5736918.

Остатки и стандартные остатки:

Наблюдение	Предсказанное Yi	Остатки	Стандартные остатки
1	19,37086397	0,020271532	0,005724072
2	20,94862	-1,404722425	-0,396651406
3	23,58256065	6,942079081	1,960234548
4	23,81452089	-2,725223896	-0,769521345
5	24,76393954	3,195076828	0,902193696
6	25,73898172	-0,236137	-0,066858749
7	27,71468957	-0,238188757	-0,067257348
8	28,36067187	-3,922599581	-1,107624262
9	28,67354847	-1,426892945	-0,402911695
10	29,36538337	-1,004378055	-0,283606185
11	29,76187355	0,906330148	0,255920402
12	31,7348842	-2,586707926	-0,730408597
13	39,47453429	0,061429642	0,017345885
14	40,16906641	-1,597346015	-0,45104252
15	40,28639513	-1,581979776	-0,446703556
16	42,40910105	-0,697794	-0,197036247
17	42,61543	1,313684547	0,370945044
18	43,96404382	5,590747927	1,578659233
19	49,74686654	3,591225292	1,014054119
20	51,93700276	5,433907746	1,534372278
21	52,15008252	-5,561712407	-1,570460474
22	52,18110046	-3,082918689	-0,870523607
23	52,4575647	0,081375322	0,022977946
24	53,94103135	-3,19379511	-0,901831
25	57,66857846	1,057481488	0,298600
26	59,05089965	-3,036249959	-0,85734576
27	59,29634595	1,872591833	0,528763669
28	60,51144	9,762454753	2,756623895
29	61,30037454	-3,152820522	-0,890261784
30	63,56063827	-4,37854827	-1,236370472

Новое равнение регрессии сравним с первоначальным:

y = 3*x + 4 а

Коэффициент при переменной X отклоняется от истинного значения приблизительно на а0,05402. При этом константа изменяется по сравнению с заданной приблизительно на 0, 6409.

Заключение

В данном случае максимально близким к истинной зависимости будет следующее равнение:

y<= 3,827144*x<+ 4,032964241.

Оно получается при дисперсии 0,5, неизменной выборке X, минимально измененной выборке Y. В этом случае коэффициент детерминации R<² максимален (0,575198),

стандартные ошибки коэффициентов минимальны (Y: 0,155289144; X: 0,011690882).

Сравнивая полученные для каждого вычисления графики, также можно прийти к выводу о том, что указанное ранее равнение является наиболее точным по отношению к истинной зависимости.

Чем меньше дисперсия выборки и изменения выборок X иY, тем точнее равнение линейной регрессии по отношению к истинной зависимости.

Таким образом, на основе данных, полученных в результате исследования, можно сделать следующие выводы:

Ø X иY.

Blog

Исследование регрессии на основе численных данных

Преподаватель:

Токмачев М.С.

Студента группы <№ 3311

Jannat

ПЛАН

1. Понятие регрессии

3. Модель парной линейной регрессии

II. Исследование регрессии при выборке из генеральной совокупности N(0;0,5)

3. Модель парной линейной регрессии