Читайте данную работу прямо на сайте или скачайте
Законы сохранения в механике
ЗМ
СТ
TOC o "1-2" h z ВСТУП.. 2
ЗАКОН ЗБЕРЕЖЕННЯ ЕНЕРГ
п СИСТЕМИ. 3
1.1. Потенцальна енергя системи. 3
1.2. Кнетична енергя системи. 6
1.3. Класифкаця сил. 7
1.4. Закон збереження енергÿ. 8
II. ЗАКОН ЗБЕРЕЖЕННЯ
МПУЛЬСУ. 12
2.1.
мпульс частинки. 12
2.2.
мпульс системи. 12
2.3. Закон збереження мпульсу. 14
. ЗАКОН ЗБЕРЕЖЕННЯ МОМЕНТУ
МПУЛЬСУ.. 18
3.1. Момент мпульсу частинки. 18
3.2. Рвняння моментв. 19
3.3. Момент мпульсу момент сили вдносно ос. 21
3.4. Закон збереження моменту мпульсу. 23
ВИСНОВОК.. 29
Л
ТЕРАТУРА.. 31
ВСТУП
Закони збереження енергÿ, мпульсу та моменту мпульсу вдносяться до числа тих найбльш фундаментальних принципв фзики, значення яких важко переоцнити. Роль цих законв особливо зросла псля того, як вияснилось, що вони далеко виходять за рамки механки представляють собою нверсальн закони природи. До цих пр не було виявлено жодного явища, де б порушувались ц закони. Вони безпомилково дють в област елементарних частинок, в област космчних обТ
ктв, у фзиц атома фзиц твердого тла та являються одними з тих небагатьох загальних законв, як лежать в основ сучасно
Вдкривши можливсть ншого пдходу до розгляду класичних механчних явищ, закони збереження стали потужним нструментом дослдження, яким кожного дня користуються фзики. Ця найважливша роль законв збереження як нструмента дослдження обумовлена рядом причин.
1. Закони збереження не залежать н вд тра
кторй частинок, н вд характеру дючих сил. Тому вони дозволяють отримати ряд досить загальних важливих висновкв про властивост рзних механчних процесв, не занурюючись в
2. Той факт, що закони збереження не залежать вд характеру дючих сил, дозволя
використовувати
3. Навть в тих випадках, коли сили вдом, закони збереження допомагають розвТязувати багато задач про рух частинок. Вс ц задач можуть бути розвТязан за допомогою рвнянь руху, але застосування законв збереження дуже часто дозволя
отримувати розвТязок бльш простим шляхом.
ЗАКОН ЗБЕРЕЖЕННЯ ЕНЕРГ
п СИСТЕМИ.
Розглянемо замкнуту систему, мж частинками яко
Покажемо, що в довльнй систем вдлку робот всх цих сил при переход системи частинок з одного стану в нший може бути представлена як спадання деяко
Спочатку взьмемо систему з двох частинок. Обчислимо елементарну роботу сил, з якими ц частинки вза
модють мж собою. Нехай в довльнй систем вдлку в деякий момент часу розташування частинок визнача
ться радус векторами 
а 
ачастинки здйснили перемщення 
а 
, то робот сил вза
модÿ 
а 
абуде дорвнювати:
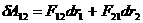
Тепер врахову
мо, що згдно третього закону Ньютона 
Введемо вектор 
, який характеризу
положення 1‑
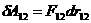
Сила Ц центральна, тому робот ц㺿 сили дорвню
спаданню потенцально
Оскльки функця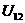 
азалежить лише вд вдстан 
амж частинками, то зрозумло, що робот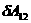 
ане залежить вд вибору системи вдлку.
Тепер звернемось до системи з трьох частинок. Елементарна робота, яку здйснюють вс сили вза
модÿ при елементарному перемщенн всх частинок, може бути представлена як сума елементарних робт всх трьох пар вза
модй, тобто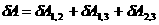 
. Але для кожно
,
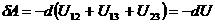де функця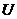 
а
власною потенцальною енергúю дано
.
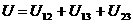Оскльки кожний доданок ц㺿 суми залежить вд вдстан мж вдповдними частинками, то очевидно, що власна потенцальна енергя 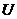адано
Зрозумло, що подбн роздуми справедлив для системи з довльного числа частинок. Тому можна стверджувати, що кожнй конфгурацÿ довльно
при скнченному перемщенн всх частинок системи
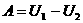
де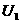 
а 
Ц значення потенцально
Власна потенцальна енергя системи 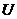Ц величина неадитивна,
тобто вона не дорвню
в загальному випадку сум власних потенцальних енергй ? частин. Необхдно врахувати ще й потенцальну енергю вза
модÿ 
аокремих частин системи:
де 
Ц власна потенцальна енергя 
Слд також мати на ваз, що власна потенцальна енергя системи, як потенцальна енергя вза
модÿ кожно
Запишемо формули для розрахунку власно
де 
Ц потенцальна енергя вза
модÿ 
Перекона
мося у справедливост ц㺿 формули спочатку для системи з трьох частинок. Вище було показано, що власна потенцальна енергя дано
бо зрозумло, що 
. Тод:
Згрупу
мо члени з однаковим першим ндексом:
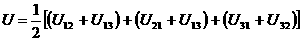
Кожна сума в круглих дужках представля
собою потенцальну енергю авза
модÿ
що повнстю вдповда
формул (1).
Узагальнення отриманого результату на довльну систему очевидне, оскльки зрозумло, що подбн мркування зовсм не залежать вд числа частинок, як складають систему.
Для системи, вза
модя мж частинками яко
Якщо розподлення маси (заряду) в систем неперервне, то додавання зводиться до нтегрування:
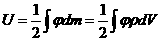
де 
Ц обТ
мна густина маси
(заряду),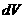 
Ц елемент обТ
му.
Тут нтегрування проводиться по всьому обТ
му, що займають маси (заряди).
1.2. Кнетична енергя системи.
Розглянемо в деякй систем вдлку довльну систему частинок. Нехай 
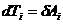
де 
Ц сумарна кнетична енергя системи. Зауважимо, що кнетична енергя системи - величина адитивна:
вона дорвню
сум кнетичних енергй окремих частин системи незалежно вд того, вза
модють вони мж собою чи н.
Отже, прирст кнетично
при кнцевому перемщенн:
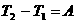
Рвняння (2) можна представити
в ншй форм подливши обидв частинки його на вдповдний промжок часу 
тобто похдна кнетично
Рвняння (2)‑(4) справедлив як в нерцальних, так в ненерцальних системах вдлку. Слд тльки розумти, що в ненерцальних системах крм роботи сил вза
модÿ необхдно враховувати роботу сил нерцÿ.
1.3. Класифкаця сил.
Вдомо, що частинки системи, яка розгляда
ться, можуть вза
модяти як мж собою, так з тлами, що не входять в дану систему. У звТязку з цим дан сили вза
модÿ мж частинками системи називають внутршнми, сили, як зумовлен дúю нших тл, що не входять в дану систему - зовншнми. В ненерцйнй систем вдлку до останнх вдносять сили нерцÿ.
Крм того, вс сили подляють на потенцальн непотенцальн. Потенцальними називають сили, як залежать при даному характер вза
модÿ лише вд конфгурацÿ механчно
До непотенцальних сил вдносять так зван дисипативн сили - це сили тертя опору. Важливою особливстю даних сил
те, що сумарна робот внутршнх дисипативних сил системи, яка розгляда
ться, вдТ
мна, причому в будь-якй систем вдлку. Доведемо це.
Довльна дисипативна сила може бути представлена у вигляд:
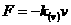
де 
Ц швидксть даного тла вдносно ншого тла (або середовища), з яким воно вза
модú; 
Ц додатнй коефцúнт,
який залежить в загальному випадку вд швидкост 
азавжди напрямлена протилежно до вектора
Переходячи до доведення цього, вдмтимо перш за все, що внутршн дисипативн сили в данй систем будуть зустрчатися попарно, причому в кожнй пар, вдповдно до третього закону Ньютона, вони однаков по модулю протилежн за напрямом. Знайдемо елементарну роботу довльно
Тепер врахову
мо, що 
Ц швидксть тла 1
вдносно тла 2, також те, що 
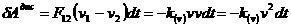
Звдси видно, що робот довльно
1.4. Закон збереження енергÿ.
Вище було показано, що прирст кнетично
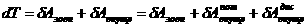
Тепер враху
мо, що робот внутршнх потенцальних сил дорвню
спаду власно
введемо поняття повно
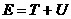
очевидно, енергя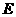 
азалежить вд швидкост частинок системи, характеру вза
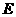
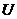
модÿ мж ними та конфгурацÿ системи. Крм того, енергя 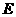асистеми не дорвню
в загальному випадку сум енергй ? окремих частин. Тод:
де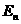 
Ц механчна енергя Ц потенцальна енергя вза
модÿ ? окремих частин.
Повернемося до формули (5). Перепишемо ? з врахуванням (6) у вигляд:
Цей вираз справедливий при нескнченно малй змн конфгурацÿ системи. При скнченнй змн матимемо:
тобто прирст механчно
Рвняння (7) можна представити
в ншй форм, подливши обидв частини на вдповдний промжок часу
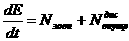
тобто похдна механчно
Рвняння (7)‑(9)
справедлив як в нерцальнй, так в ненерцальнй системах вдлку. Слд тльки мати на ваз, що в ненерцальнй систем вдлку необхдно врахувати роботу (потужнсть) сил нерцÿ, як вдграють роль зовншнх сил, тобто пд
аслд розумти алгебра
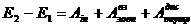
Отже, ми прийшли до важливого висновку: механчна енергя системи може змнюватися пд дúю як зовншнх сил, так внутршнх дисипативних сил (тобто пд дúю алгебра
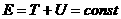
Таку систему називають консервативною. Зауважимо, що при рус замкнуто
Дал, з рвняння (8) виплива
, що якщо замкнута система неконсервативна, тобто в нй присутн дисипативн сили, то механчна енергя тако
Можна сказати: зменшення механчно
Бльш глибоке осмислення цього питання привело до фундаментального висновку про снування в природ нверсального закону збереження енергÿ:
енергя нколи не виника
не зника
, вона може лише переходити з одн㺿 форми в ншу, або обмнюватися мж окремими частинами матерÿ.
При цьому поняття енергÿ довелось розширити введенням нових форм ? - енергя електромагнтного поля, хмчна енергя, ядерна енергя та н.
Унверсальний закон збереження енергÿ охоплю
, таким чином, т фзичн явища, на як закони Ньютона не поширюються, Тому вн не може бути виведеним з цих законв, повинен розглядатися як самостйний закон, який представля
собою одне з найбльш широких загальнень дослдних фактв.
Повертаючись до рвняння (12), можна сказати: при зменшенн механчно
Механчна енергя може збергатися й у незамкнутих системах, але це вдбува
ться лише в тих випадках, коли згдно з рвнянням (8) зменшення ц㺿 енергÿ за рахунок роботи проти внутршнх дисипативних сил компенсу
ться надходженням енергÿ за рахунок роботи зовншнх сил.
II. ЗАКОН ЗБЕРЕЖЕННЯ
МПУЛЬСУ.
Досвд вдповдний аналз механчних уявлень показують, що для характеристики механчного руху тл крм кнетично
Перейдемо до бльш детального вивчення мпульсу. Перш за все запишемо основне рвняння динамки Ньютона через мпульс:
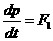
тобто похдна мпульсу матерально
Зауважимо, що в ненерцальнй систем вдлку сила авключа
в себе не тльки сили вза
модÿ дано
Рвняння (13) дозволя
знайти прирст мпульсу частинки за довльний промжок часу, якщо вдома залежнсть сили авд часу. Дйсно, з
(13) виплива
, що елементарний прирст мпульсу частинки за промжок часу а
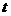
Якщо сила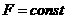 
аможна винести з-пд нтеграла тод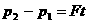 
2.2.
мпульс системи.
Розглянемо довльну систему частинок. Введемо поняття мпульсу системи як векторну суму мпульсв ? окремих частинок:
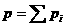
де 
Ц мпульс
Знайдемо фзичну величину, яка визнача
змну мпульсу системи. Для цього продиференцю
мо рвняння (14) по часу:
ле 
Ц сила, що дú на матеральну точку. Тод:
де 
а- сили, що дють на 
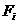Ц сила, що дú на цю ж частинку збоку нших тл, як не входять в розглядувану систему (зовншн сили). Пдставивши останнй вираз в попереднй, отрима
мо:
Подвйна сума справа - це сума всх внутршнх сил. Вдповдно до третього закону Ньютона сили вза
модÿ мж частинками системи попарно однаков по модулю протилежн за напрямком. Тому результуюча сила в кожнй пар вза
модÿ дорвню
нулю, тому дорвню
нулю векторна сума всх внутршнх сил. В результат рвняння прийме вигляд:
де Ц результуюча всх зовншнх сил,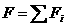 
Рвняння (15) означа
: похдна мпульсу системи по часу дорвню
векторнй сум всх зовншнх сил, що дють на частинки системи.
з рвняння (15) виплива
, що прирст мпульсу системи за скнчений промжок часу 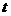абуде:
тобто прирст мпульсу системи дорвню
мпульсу результуючо
Рвняння (15) (16) справедлив як в нерцальнй, так в ненерцальнй систем вдлку. Слд тльки мати на уваз, що в ненерцальнй систем вдлку необхдно враховувати дю сил нерцÿ, що вдграють роль зовншнх сил.
2.3. Закон збереження мпульсу.
Застосування другого та третього законв динамки до системи, яка склада
ться з деклькох вза
модючих тл, приводить до дуже важливих висновкв, з яких виплива
закон збереження мпульсу.
Розглянемо систему, яка склада
ться з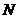 
ачастинок (матеральних точок). Позначимо через асилу, з якою 
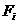апозначимо результуючу всх зовншнх сил, що дють на 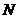ачастинок:
...
а
...
а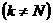
(Ц мпульс
Додамо вс ц рвняння. Злва отрима
мо похдну по часу вд сумарного мпульсу системи:
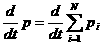
Справа вдмнною вд нуля буде лише сума зовншнх сил 
Згдно з третм законом Ньютона кожна з дужок буде дорвнювати нулю. Вдповдно, сума внутршнх сил, що дють на тла системи, завжди дорвню
нулю:
Тод отрима
мо:
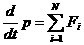
Таким чином, похдна по часу вд сумарного мпульсу системи дорвню
сум зовншнх сил, як дють на тла системи.
Якщо система замкнута, зовншн сили вдсутн права частина останнього рвняння дорвню
нулю. Тому вдповдно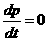 
Таким чином, ми прийшли до важливого висновку, саме - закону збереження мпульсу:
в нерцальнй систем вдлку мпульс замкнуто
При цьому мпульси окремих частинок замкнуто
В цьому розумнн рвняння (15) (16) слд розглядати як бльш загальне формулювання закону збереження мпульсу, в якому вказана причина змни мпульсу в незамкнутй систем - дя нших тл (зовншнх сил). Вище сказане, зрозумло, справедливе по вдношенню до нерцальних систем вдлку.
мпульс може збергатися в незамкненй систем при умов, що результуюча всх зовншнх сил дорвню
нулю. Це безпосередньо витка
з рвнянь (15) (16). У практичному вдношенн збереження мпульсу в цих випадках явля
особливий нтерес, тому що да
можливсть отримувати досить простим шляхом ряд свдчень про поведнку системи, не заглиблюючись в детальний розгляд процесу.
У незамкнутй систему може збергатися не сам мпульс, його проекця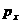 
ана деякий напрям 
ана напрямок адорвню
нулю, тобто вектор аперпендикулярний йому.
Дйсно, спроектувавши рвняння (15), отрима
мо:
звдки виплива
, що якщо 
В основ закону збереження мпульсу лежить однорднсть простору, тобто однаковсть властивостей простору в сх точках. Паралельне перенесення замкнуто
Роздуми, як привели нас до закону збереження мпульсу, цлком спиралися на справедливсть законв Ньютона. Вважалося, що матеральн точки замкнуто
що вдбува
ться у випадку систем, як не пдкоряються законам Ньютона, наприклад в системах з електромагнтним випромнюванням?
Вдповдь на це запитання да
досвд, який показу
, що закон збереження мпульсу виявля
ться справедливим для таких систем. Однак в цих випадках в загальному баланс мпульсу необхдно враховувати не лише мпульси частинок, але й мпульс, яким володú саме поле випромнювання.
Таким чином, досвд показу
, що закон збереження мпульсу явля
собою фундаментальний закон природи, який не зна
жодних виняткв. Але в такому широкому розумнн вн вже не
наслдком законв Ньютона, повинен розглядатися як самостйний загальний принцип, що
узагальненням фактв.
. ЗАКОН ЗБЕРЕЖЕННЯ МОМЕНТУ
МПУЛЬСУ
налз поведнки систем показу
, що крм енергÿ та мпульсу сну
ще одна механчна величина, з якою також повТязаний закон збереження - це момент мпульсу. що це за величина як ? властивост?
|
|
|
|
Рис. 1 |
Рис. 2 |
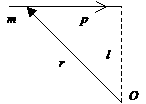
Взьмемо спочатку одну частинку. Нехай
Ц радус-вектор, який характеризу
? положення вдносно деяко
Модуль ц㺿 величини, що дорвню
ампульсу на модуль вектора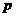 
Частинка володú моментом мпульсу незалежно вд форми тра
кторÿ, по якй вона руха
ться. Розглянемо два випадки.
|
|
|
Рис. 3 |
1. Частинка руха
ться вздовж прямолнйно
|
|
|
Рис. 4 |
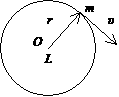
2. Частинка руха
ться по колу радуса
а(рис. 4). Модуль моменту мпульсу вдносно центру кола дорвню
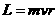а так само, як в попередньому випадку, може змнюватися лише за рахунок змни модуля швидкост.
Не дивлячись на неперервну змну напряму вектора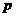 
азалиша
ться постйним.
3.2. Рвняння моментв.
Тясу
мо яка механчна величина вдповда
за змну вектора ав данй систем вдлку. Для цього продиференцю
мо рвняння (17) по часу:
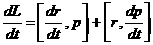
Оскльки точка 
а
нерухомою, то вектор
адорвню
швидкост ачастинки, тобто спвпада
за напрямком з вектором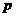
Дал, згдно з другим законом Ньютона,
Ц рвнодйна всх сил,
як прикладен до частинки. Вдповдно:
Величину, що сто
Модуль цього вектора дорвню
:
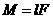
де Ц довжина перпендикулярна, опущеного з точки ана пряму, вздовж яко
Отже, похдна по часу вд моменту мпульсу ачастинки вдносно деяко
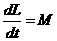
Це рвняння назива
ться рвнянням моментв. Зауважимо, що якщо система вдлку
ненерцальною, то момент сили 
авключа
в себе як момент сил вза
модÿ, так момент сил нерцÿ (вдносно т㺿 ж точки
з рвняння моментв (18) слду
,
що якщо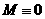 
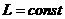
авибрано
1)
знайти момент сили авдносно довльно
2)
визначити прирст моменту мпульсу частинки вдносно точки аза довльний промжок часу, якщо вдома залежнсть вд часу моменту сили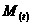 
Виршення першого питання зводиться до знаходження похдно
Виршення другого питання зводиться до нтегрування рвняння (18). Помноживши обидв частини цього рвняння на 
Ц вираз, який визнача
елементарний прирст вектора аза скнчений промжок часу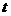
Величину, яка сто
3.3. Момент мпульсу момент сили вдносно ос.
Взьмемо в деякй систем вдлку довльну нерухому всь 
ана ос амомент мпульсу частинки 
адорвню
Моментом мпульсу вдносно ос аназивають проекцю на цю всь вектора адано
|
|
|
Рис. 5 |
налогчно вводиться поняття моменту сили вдносно ос. пх позначають вдповдно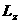 
а 
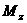
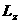ата 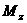ане залежать вд вибору точки ана ос
Тясу
мо властивост цих величин.
Спроектувавши (18) на всь
тобто похдна по часу вд моменту мпульсу частинки вдносно ос адорвню
моменту сили вдносно ц㺿 ос. Якщо 
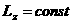
адорвню
нулю, то момент мпульсу частинки вдносно ц㺿 ос залиша
ться постйним. При цьому сам вектор аможе змнюватися.
Знайдемо тепер аналтичний вираз для 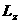а 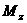авекторних добуткв 
а 
Скористу
мось цилндричною системою координат 
а(рис. 6) орти 
|
|
|
Рис. 6 |
В цй систем координат радус-вектор ата мпульс 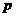ачастинки записують так:
де 
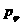
Ц проекцÿ вектора 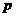ана вдповдн орти. З векторно
Звдси одразу видно, що моменти мпульсу частинки вдносно ос
де Ц вдстань частинки вд ос 
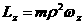
де 
Ц проекця кутово
Запишемо момент сили вдносно ос 
де 
Ц проекця вектора сили ана орт .
Звернемо вагу, що проекця 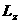а 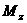адйсно не залежать вд вибору точки ана ос , вдносно яко
3.4. Закон збереження моменту мпульсу.
Виберемо довльну систему частинок. Введемо поняття моменту мпульсу дано
де вс вектори визначен вдносно одн㺿 т㺿 ж точки азадано
Тясу
мо, яка величина визна
змну моменту мпульсу системи. Для цього продиференцю
мо (19) по часу:
похдна 
адорвню
моменту всх сил, що дють на 
. Тод:
Тут перша сума - це сумарний момент всх внутршнх сил вдносно точки , друга сума - сумарний момент всх зовншнх сил вдносно т㺿 ж точки .
Покажемо, що сумарний момент всх внутршнх сил вдносно довльно
В результат останн
рвняння прийма
вигляд:
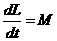
де Ц сумарний момент всх зовншнх сил, 
.
Рвняння (20) стверджу
: похдна моменту мпульсу системи по часу дорвню
сумарному моменту всх зовншнх сил.
Як у випадку одн㺿 частинки, з рвняння (20) виплива
, що прирст моменту мпульсу системи за скнчений промжок часу :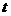
тобто прирст моменту мпульсу системи дорвню
мпульсу сумарного моменту всх зовншнх сил за вдповдний промжок часу.
тут обидва моменти, а , визначен вдносно одн㺿 т㺿 ж точки авибрано
Рвняння (20) (21) справедлив як в нерцйнй, так в ненерцйнй системах вдлку. Тльки в ненерцальнй систем вдлку потрбно враховувати дю сил нерцÿ, як вдграють роль зовншнх сил, тобто за ав цих рвняннях приймати суму 
, де 
Ц сумарний момент зовншнх сил вза
модÿ, 
Ц сумарний момент сил нерцÿ (вдносно одн㺿 т㺿 ж точки асистеми вдлку).
Отже, ми прийшли до важливого висновку: згдно з рвнянням (20), момент мпульсу системи може змнюватися пд дúю лише сумарного моменту всх зовншнх сил. Звдси безпосередньо виплива
нший важливий висновок - закон збереження моменту мпульсу:
в нерцальнй систем вдлку момент мпульсу замкнуто
Причому це справедливо для моменту мпульсу, взятого вдносно будь-яко
Таким чином, в нерцальнй систем вдлку момент мпульсу замкнуто
Яксним пдтвердженням закону збереження моменту мпульсу може бути дослд з лавкою Жуковського. Демонстрацйна лавка, яку запропонував Жуковський, явля
собою металевий круг, який оберта
ться з досить малим тертям навколо вертикально
Закон збереження моменту клькост руху справедливий для системи твердих тл. При додаванн рвнянь руху рвнянь моментв внутршн сили моменти внутршнх сил вза
мно знищуються. Тому якщо момент зовншнх сил, що дють на систему, дорвню
нулю, то загальний момент клькост руху системи залиша
ться незмнним.
Так сила тяжння, що дú з боку Сонця, не може змнити швидкост обертання Земл навколо ос. п
Уже з цього прикладу видно, що застосовуючи закон збереження моменту мпульсу до системи тл, потрбно памТятати, що при цьому тла часто розглядати як матеральн точки. Тверде тло може обертатися навколо ос, що проходить через нього, розглядаючи тло як точку, ми не врахову
мо момент мпульсу.
з закону збереження моменту мпульсу виплива
, що внутршн сили не можуть змнити момент мпульсу тла або системи тл, однак це не означа
, що внутршн сили не можуть змнити момент мпульсу тла або системи тл. Однак це не означа
, що внутршн сили не можуть визвати обертання частин всередин системи. Якщо деяка частина системи почина
обертатися в одному напрям, то нша, екввалентна ? частина почне обертатися в протилежному напрям так, що в цлому для системи закон збереження моменту мпульсу буде виконуватися.
Закон збереження моменту мпульсу вдгра
таку ж важливу роль, як закони збереження енергÿ та мпульсу. же сам по соб вд дозволя
зробити в деяких випадках ряд сутт
вих висновкв про властивост тих чи нших процесв, зовсм не вникаючи в
Особливий нтерес викликають випадки,
коли момент мпульсу азберга
ться для незамкнутих систем, у яких, як вдомо, мпульс 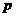азмню
ться з часом. Якщо вдносно деяко
У бльш обмеженому випадку в незамкнутих системах може збергатися не сам момент мпульсу , його проекця на деяку нерухому всь . Це бува
тод, коли проекця сумарного моменту авсх зовншнх сил на цю всь дорвню
нулю. Дйсно, спроектувати рвняння (20) на всь , сприйма
мо:
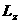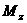тут а Ц момент мпульсу
сумарний момент зовншнх сил вдносно ос :
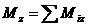
де 
а 
Ц момент мпульсу
момент зовншнх сил вдносно ос адля
з рвняння (22) виплива
, що якщо вдносно деяко
При цьому сам вектор ана цй ос, може змнюватися. Наприклад, якщо система руха
ться в однордному пол тяжння, то сумарний момент всх сил тяжння вдносно довльно
Мркування, як приводять до закону збереження моменту мпульсу, цлком спираються на справедливсть законв Ньютона.
Враховуючи значну роль, яку вдгра
закон збереження моменту мпульсу в механц, у фзиц поняття моменту мпульсу поширюють на немеханчн системи (як не пдкоряються законам Ньютона) постулюють закон збереження моменту мпульсу для всх фзичних процесв.
Такий розширений закон збереження моменту мпульсу же не
наслдком законв Ньютона, явля
собою самостйний загальний принцип, який
загальненням дослдних фактв. Поряд з законами збереження енергÿ та мпульсу закон збереження моменту мпульсу
одним з найважливших фундаментальних законв природи.
ВИСНОВОК
Кожен з розглянутих законв збереження
нкальним явля
ться
законом природи.
1. Повна енергя (сума кнетично
Енергя нколи не виника
не зника
. Вона лише переходить з одного виду в нший.
Закон збереження перетворення енергй вдкритий у 1840 р. Р. Май
ром. Незважаючи на те, що вчений здйснив вдкриття на основ медико-бологчних дослджень, вдкритий ним закон виявився справедливим для с㺿 природи.
2. Повний мпульс замкнуто
3.
При вдсутност моменту зовншнх сил (
Закони збереження розглядаються у шкльному курс фзики в 9 клас. Вводяться поняття енергÿ, мпульсу та вдповдно закони збереження енергÿ та мпульсу, однак момент мпульсу вивча
ться лише поверхнево. Оскльки ц закони
дуже важливими необхдними для кращого опанування матералу, то в школ слд детальнше вивчати дану тему.
Л
ТЕРАТУРА
1. Архангельський М.М. Курс физики. Механика. - М.: Просвещение, 1975. - с. 186‑190
2. Иродов И.Е. Основные законы механики. - М.: Высшая школа, 1978. - с. 62‑64, 82‑91, 100‑105, 129‑140
3. Савельев И.В. Курс физики. Механика. Молекулярная физика. - М.: Наука, 1989. - т. 1 - с. 57‑60, 89‑92
4. Стрелков С.П. Механика. - М.: Наука, 1975. - с. 95‑96