Читайте данную работу прямо на сайте или скачайте
Устойчивость и стабилизация движений относительно части переменных при постоянно действующих возмущениях
Реферат
Дипломная работ содержит 59 страниц, 42 использованных источника, 3 рисунка.
УСТОЙЧИВОСТЬ, СТАБИЛИЗАЦИЯ, ЧАСТИЧНАЯ УСТОЙЧИВОСТЬ, ЧАСТИЧНАЯ СТАБИЛИЗАЦИЯ, ПОСТОЯННО ДЕЙСТВУЮЩИЕ ВОЗМУЩЕНИЯ, ЧАСТЬ ПЕРЕМЕННЫХ, ЛИНЕЙНАЯ СИСТЕМА, НЕЛИНЕЙНАЯ СИСТЕМА.
Объект исследования - динамическая система.
Предмет исследования - стойчивость и стабилизация движения относительно части переменных при постоянно действующих возмущениях.
Цель работы - исследование стойчивости и стабилизации линейных и нелинейных систем относительно части переменных при постоянно действующих возмущениях; анализ научной и учебной литературы по теме исследования.
Методы исследования - в основу исследования теории стойчивости и стабилизации относительно части переменных при постоянно действующих возмущениях положены основные задачи частичной стойчивости Ляпунова, Румянцева, Воротникова. При решении полученных математических задач используется метод, основанный на нелинейной замене переменных, метод функций Ляпунова, где рассматривается ряд теорем об устойчивости движения относительно части переменных при постоянно действующих возмущениях.
Полученные результаты - проанализирована научная и учебная литература по исследуемой теме, приведены основные определения и теоремы и словия стойчивости движения твердого тела с одной неподвижной точкой при постоянно действующих возмущениях; с помощью метода функций Ляпунова рассмотрен ряд теорем об стойчивости движения относительно части переменных при постоянно действующих возмущениях, приводится обобщение теорема Ляпунова - Малкина об стойчивости и (одновременно) экспоненциальной асимптотической стойчивости по части переменных по линейному приближению, рассмотрена оптимальная стабилизация одной нелинейной системы при наличии постоянно действующих возмущений, исследована математическая модель на словие стойчивости и стабилизации движения относительно части переменных при постоянно действующих возмущениях.
Область применения - в нелинейной теории правления, механике, биологии, экономике, на стыке физики, химии и теории правления, в системах с распределенными параметрами (в частных производных), в стохастических, дискретных, также в абстрактных динамических системах в метрическом пространстве.
Содержание
Введение 7
1 стойчивость линейных систем 13
1.1 Определение и основные теоремы а 13
13
1.2 стойчивость движения твердого тела с одной неподвижной точкой 19
1.3 гебраический критерий асимптотической  23
23
1.4а словие стойчивости и асимптотической устойчивости при не
малых постоянных возмущениях 24
1.5 Обобщение теоремы Ляпунова - Малкин 30
2 стойчивость нелинейных систем 32
2.1 стойчивость адвижения аотносительно ачасти апеременных при
постоянно действующих возмущениях для нелинейных систем
(1 случай) 32
2.1.1 Основные определения и теоремы 32
2.1.2 Пример адвижения аголономной амеханической асистемы 36
2.1.3 Распространение принципа сравнения с вектор - функциейа
Ляпунова на задачу  а- стойчивости апри апостоянно
а- стойчивости апри апостоянно
действующих возмущениях 37
2.2 стойчивость движения относительно части переменных при
постоянно действующих возмущениях для нелинейных систем
(2 случай) 38
2.3 Оптимальная стабилизация одной нелинейной системы при
наличии постоянно действующих возмущений 40
3 стойчивость и стабилизация движения асимметричного твердого тел 45
3.1 Стабилизация по части переменных перманентного вращения асимметричного твердого тела посредством одного маховик 45
3.2 стойчивость и стабилизация движения асимметричного твердого
тел 47
3.3 Динамическое уравнение Эйлера, описывающее гловое движение твердого тела под действием управляющих моментов 51
3.4 Динамическое уравнение Эйлера, описывающее гловое движение твердого тела под действием постоянно действующих возмущений 52
Заключение 54
Список использованных источников 56
Введение
Дипломная работ посвящена разделу общей теории стойчивости, в котором, в отличие от традиционных исследований в этой области, рассматриваются задачи стойчивости и стабилизации динамических систем не по всем, лишь по отношению к заданной части характеризующих их переменных. Такие задачи естественным образом возникают в приложениях, как из требования нормального функционирования, так и при оценке возможностей системы.
Начиная с середины XX столетия эти задачи, затем и тесно связанные с ней задачи стабилизации по отношению к части переменных стали систематически разрабатываться в научных центрах России и бывшего Р, также Европы, США, Индии, Японии и Китая. Благодаря большой математической общности постановки указанные задачи являются междисциплинарными и естественным образом возникают при моделировании многих явлений и правляемых процессов в самых разных разделах науки: механике, физике, экономике, биологии, и других. Они часто называются также задачами частичной стойчивости (стабилизации).
Начиная с основополагающих работ В.В. Румянцева [28 - 31], которые привлекли к задачам устойчивости по отношению к части переменных внимание многих ченых, ведущим методом исследования является метод функций Ляпунова, оказавшийся весьма эффективным при анализе как теоретических, так и прикладных проблем.
Однако хотя во многих важных прикладных задачах метод функций Ляпунова и позволяет получить строгие и легко интерпретируемые словия стойчивости по части переменных, тем не менее, в целом вопросы конструктивного построения функций Ляпунова остаются малоизученными. В такой ситуации значительный интерес представляет как дальнейшее развитие метода в плане ослабления требований к функциям Ляпунова и казания конструктивных путей их построения, так и развитие других подходов к задачам стойчивости по отношению к части переменных.
Исследование стойчивости относительно части переменныха позволяет выявить дополнительные свойства модели, которые не видны при исследовании лполной стойчивости. Перечислим некоторые из обнаруженных к настоящему времени таких возможностей, не имеющих места при исследовании стойчивости по отношению ко всем переменным [6].
1 Допустимость стойчивости в малом одной группы переменных при больших начальных возмущениях другой их группы ( 
 аили при больших
аили при больших 
2 Возможность инвариантности свойств устойчивости по части переменных при сколь годно больших постоянно действующих возмущениях [27], действующих по некоторым каналам системы.
3 Допустимость асимптотического характера стойчивости по части переменных при постоянно действующих возмущениях [4, 5].
Развитие исследований, проведенных к настоящему времени, можно словно разделить на два этапа. Первый этап (конец 50-х - начало 70-х годов XX века) связан почти исключительно с развитием метода функций Ляпунова и подытожен (по работам [12, 21, 24, 28, 29, 31, 36, 38, а40, 41, 42]) в обзорной статье А.С. Озиранера и В.В. Румянцева [26], сыгравшей существенную стимулирующую роль в инициировании дальнейшего исследования проблемы стойчивости (стабилизации) по части переменных.
Начиная с середины 70-х годов прошлого столетия (второй этап исследований) круг вопросов, решаемых в рамках данной проблемы, значительно расширился. В числе их оказались следующие направления исследований.
1 Дальнейшее развитие метода функций Ляпунова применительно к задаче стойчивости и стабилизации по части переменных при постоянно действующих возмущениях (п.д.в.) для систем обыкновенных дифференциальных уравнений. Потребность в этом, в частности, возникла вследствие ряда выявленных на первом этапе исследований существенных трудностей при переносе основных теорема метода функций Ляпунова на случай задачи стойчивости аи стабилизации по части переменных при постоянно действующих возмущениях (Озиранер А.С, Румянцев В.В.[26], Гермаидзе В.Е., Красовский Н.Н. [10]).
2 В работах К. Кордуняну [37], Каримова А.У.[14], Озиранера А.С. [25], Мики К., Масамиси А., Шойси С. [39], Игнатьева А.О.[13] метод функции Ляпунов используется для решения задач стойчивости по части переменным при постоянно действующих возмущениях и сохранения стойчивости. Одной из особенностей задачи устойчивости и стабилизации по части переменных при постоянно действующих возмущениях является ее отличный, в сравнении со случаем стойчивости и стабилизации при постоянно действующих возмущениях по отношению ко всем переменным, характер взаимоотношений с задачей частичной стойчивости при структурных (параметрических) возмущениях. Это видно же на примере асимптотической стойчивости по отношению к части переменных линейной стационарной системы, которая, будучи стойчива по этим переменным при постоянно действующих возмущениях, может, вообще говоря, терять стойчивость по казанным переменным даже при малых возмущениях своих коэффициентов. Именно задачи частичной устойчивости (стабилизации), в отличии от задач стойчивости (стабилизации) по всем переменным, становятся строгой математической базой для многих важных современных исследований.
Объект исследования - динамическая система.
Предмет исследования - стойчивость и стабилизация движений относительно части переменных при постоянно действующих возмущениях.
Цель исследования - анализ стойчивости и стабилизации динамических систем по отношению к части переменных.
Для достижения поставленной цели необходимо решить следующие задачи:
1) проанализировать научную литературу, посвящённую проблеме стойчивости и стабилизации движения при постоянно действующих возмущениях и применить эти исследования для решения практической задачи;
2) рассмотреть устойчивость и стабилизацию движений относительно частим переменных при постоянно действующих возмущениях для линейных систем;
3) раскрыть определение стойчивости и стабилизации движения относительно части переменных при постоянно действующих возмущениях;
4)
рассмотреть основные теоремы, исследующие словия  ;
;
5) рассмотреть устойчивость и стабилизацию движений относительно части переменных при постоянно действующих возмущениях для нелинейных систем;
6) с помощью метода функций Ляпунова рассмотреть ряд теорем об стойчивости движения относительно части переменных при постоянно действующих возмущениях;
7) рассмотреть оптимальную стабилизацию нелинейных систем при наличии постоянно действующих возмущений выявить
8) провести анализ стойчивости и стабилизации движений относительно части переменных для конкретной математической модели с использованием современных методов.
Дипломная работ состоит из 3 разделов.
Первый раздел посвящен задаче об стойчивости и асимптотической стойчивости движения относительно части переменных при постоянно действующих возмущениях, когда некоторые из них могут не быть достаточно малыми. Единообразным приемом, основанным на нелинейной замене переменных и дифференциальных неравенствах, приводятся словия стойчивости движения твердого тела с одной неподвижной точкой при постоянно действующих возмущениях.
Далее показывается, что задача об стойчивости движения относительно части переменных (

 ряд известных результатов, исходным пунктом в которых является теорема Ляпунова - Малкина об стойчивости и (одновременно)
экспоненциальной асимптотической стойчивости по части переменных по линейному приближению [1].
ряд известных результатов, исходным пунктом в которых является теорема Ляпунова - Малкина об стойчивости и (одновременно)
экспоненциальной асимптотической стойчивости по части переменных по линейному приближению [1].
Во 2 разделе дается исследование нелинейных систем. С помощью метода функций Ляпунова рассматривается ряд теорем об стойчивости движения относительно части переменных при постоянно действующих возмущениях. Опираясь на широко известную теорему Н.Н. Красовского об оптимальной стабилизации [16, а285] и метод оптимальной стабилизации линейных неоднородных правляемых систем [15, 73-83] приводиться построение правления оптимально стабилизирующего множество относительно решений уравнения.
В третьем разделе рассмотрена стабилизация по части переменных перманентного вращения асимметричного твердого тела с помощью одного маховика. Показано, что пока гиростат совершает заданное движение, маховик находится в состоянии покоя (управляющий двигатель включен). При появлении малых постоянных возмущений специальные стройства формируют и прикладывают к маховику правляющий момент, в результате основное тело гиростата с течением времени возвращается в исходный режим стационарного вращения, сам маховик - в состояние покоя. Также рассмотрен пример стойчивости (стабилизации) и правления по части переменных гловым движением асимметричного твердого тела. Рассмотрен этот же случай при постоянно действующих возмущениях.
1 стойчивость линейных систем
1.1
Определение и основные теоремы 
Пусть имеем линейную стационарную систему обыкновенных дифференциальных уравнений возмущенного движения

или в переменных 
 (1.1.1)а
(1.1.1)а
где 
Наряду с системой (1.1) рассмотрим лвозмущенную систему
 (1.1.2)
(1.1.2)
разобьем на две группы и представим  аи
аи  ав виде
ав виде 
 .
.
Определение 1.1.1 (Воротников В.И. [4]). Движение  асистемы (1.1.1)
называется
асистемы (1.1.1)
называется 
 амогут быть казаны положительные числа
амогут быть казаны положительные числа 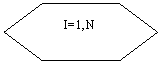
 (1.1.3)
(1.1.3)
выполняется на всех движениях системы (1.2), начинающихся в области
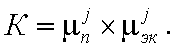 (1.1.4)
(1.1.4)
при любых значениях 
 (1.1.5)
(1.1.5)
в области (1.1.3).
Если, кроме того, 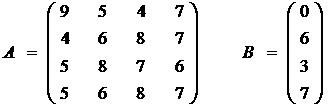 апри
апри  , то движение
, то движение
 асистемы (1.1.1)
называется асимптотически
асистемы (1.1.1)
называется асимптотически 
Замечание 1.1.1 Если вектор 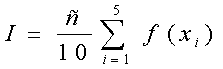
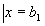 ав (1.1.5)
удовлетворяют соответственно словиям
ав (1.1.5)
удовлетворяют соответственно словиям 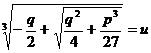 аи
аи 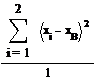
 асистемы (1.1.1)
асистемы (1.1.1) 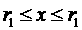
 аопределение
аопределение 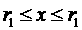

 а- в определение
а- в определение 
Замечание 1.1.2 Определение 

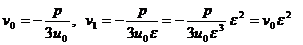
Замечание 1.1.3 Определение асимптотической  а
а 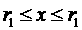
 асогласно [19].
асогласно [19].
Рассмотрим матрицы
 (1.1.6)
(1.1.6)
 (1.1.7)
(1.1.7)
где 
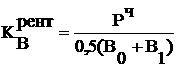

 -
линейно-независимые векторы-столбцы матрицы
-
линейно-независимые векторы-столбцы матрицы 
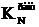 аневырожденная,
аневырожденная, 
Теорема 1.1.1 (Воротников В.И. [4]). Пусть движение  асистемы (1.1)
асимптотически
асистемы (1.1)
асимптотически 
 астроки с номерами
астроки с номерами 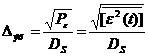 анулевые, то движение
анулевые, то движение 
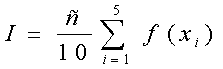 аи вектор - функцию
аи вектор - функцию 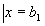 авходят соответственно переменные
авходят соответственно переменные  аи функции
аи функции  ас номерами
ас номерами 
Доказательство. Сделаем в системе (1.1) замену переменных
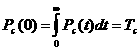
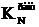 аимеет вид (1.1.7). В новых переменных уравнения системы (1.1.1), согласно [2, 7] распадаются на две группы:
аимеет вид (1.1.7). В новых переменных уравнения системы (1.1.1), согласно [2, 7] распадаются на две группы:

причем а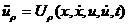 а- мерный вектор
а- мерный вектор 
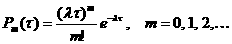 (1.1.8)
(1.1.8)
полностью определяет поведение переменных  асистемы (1.1.1).
асистемы (1.1.1).
Рассмотрим наряду с (1.1.8) систему

Движение 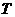 а
а 
 ане содержит возмущений
ане содержит возмущений
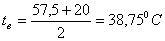

 асистемы (1.1)
асистемы (1.1) 
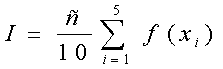 аи вектор - функцию
аи вектор - функцию 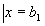 авходят соответственно переменные
авходят соответственно переменные  аи
аи 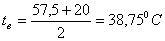 ас номерами
ас номерами 
Следствие. Если движение  асистемы (1.1)
асимптотически
асистемы (1.1)
асимптотически 
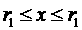
Пример 1.1.1 Пусть уравнения возмущенного движения (1.1) имеют вид
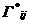 (1.1.9)
(1.1.9)

Систему (1.1.8) в данном случае составят уравнения

Собственные числа матрицы
 аимеют отрицательные части
аимеют отрицательные части 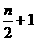 нулевая, поэтому,
согласно теореме 1.1.1, движение
нулевая, поэтому,
согласно теореме 1.1.1, движение  системы (1.1.9)
системы (1.1.9)  а
а 
 . Таким образом, невозмущенное движение системы (1.1.9)
. Таким образом, невозмущенное движение системы (1.1.9) 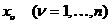
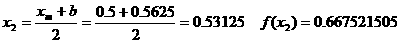
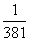
Пример 1.1.2 Рассмотрим уравнения возмущенного движения регулируемой системы в критическом случае двух нулевых корней
 (1.1.10)
(1.1.10)
где  а- постоянные числа,
а- постоянные числа, 

Введем новую переменную [3]
 , где
, где 
 (1.1.11)
(1.1.11)

Известные словия устойчивости в целом невозмущенного движения системы (1.1.11) [17] будут,
согласно [3], достаточными словиями  а любом конечном числе
а любом конечном числе 
 аможно сделать достаточно малой за счет подходящего выбора величины
аможно сделать достаточно малой за счет подходящего выбора величины 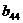
Пусть вектор - функции 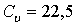 аи
аи  ав системе (1.1.2)
имеют вид
ав системе (1.1.2)
имеют вид

где 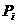 аи
аи  а- постоянные векторы соответствующих размеров.
а- постоянные векторы соответствующих размеров.
Допустим, что 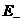
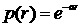
 алинейно - независимые векторы - столбцы матрицы
алинейно - независимые векторы - столбцы матрицы 
 алинейно независимы. Рассмотрим систему алгебраических уравнений для определения
алинейно независимы. Рассмотрим систему алгебраических уравнений для определения 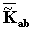 а
а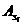

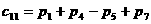
Предположим, что
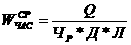 (1.1.12)
(1.1.12)
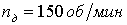 а (1.1.13)
а (1.1.13)
где 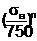 а- достаточно малые положительные постоянные.
а- достаточно малые положительные постоянные.
Теорема 1.1.2 (Воротников В.И. [4]). Если движение  асистемы (1.1.1)
асимптотически
асистемы (1.1.1)
асимптотически 
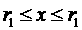

 аи любых довлетворяющих словиям (1.1.13)
возмущениях
аи любых довлетворяющих словиям (1.1.13)
возмущениях 
 астроки с номерами
астроки с номерами 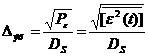 анулевые, то это движение асимптотически
анулевые, то это движение асимптотически  а- стойчиво, причем в вектор
а- стойчиво, причем в вектор 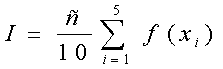 аи вектор - функцию
аи вектор - функцию 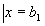 авходят соответственно переменные
авходят соответственно переменные 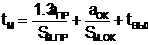 аи функции
аи функции  ас номерами
ас номерами  а.
а.
Пример 1.1.3 Пусть уравнения возмущенного движения (1.1) имеют вид
 (1.1.14)
(1.1.14)
Поскольку 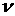
 (1.1.15)
(1.1.15)
После введения новой переменной  асистема
асистема
 априводиться к виду
априводиться к виду
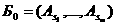
Поэтому при выполнении условий (1.1.13) невозмущенное движение системы (1.1.14) асимптотически 
Дальнейшим развитием проблемы стойчивости на класс правляемых систем является задача стабилизации движения. Эта задача имеет большое значение в связи с бурным развитием теории правления и ее обширными практическими применениями.
Рассмотрим систему уравнений возмущенного движения правляемого объекта
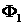
или, в переменных 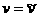
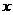 (1.1.16)
(1.1.16)
правые части определены и непрерывны в области
 (1.1.17)
(1.1.17)
Вектор правляющих воздействий  аищем в виде
аищем в виде 


 (1.1.18)
(1.1.18)
система (1.1.16) при  аудовлетворяет ограничениям, наложенным на систему (1.1.18). Пусть
аудовлетворяет ограничениям, наложенным на систему (1.1.18). Пусть 
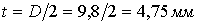
в котором 
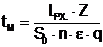

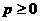
Задача оптимальной стабилизации. Найти вектор-функцию 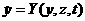
 асистемы (1.1.16)
асимптотически стойчиво относительно
асистемы (1.1.16)
асимптотически стойчиво относительно 
1.2 Устойчивость движения твердого тела с одной неподвижной точкой
Рассмотрим движение тяжелого твердого тела с одной неподвижной точкой, вызванное начальными и постоянно действующими возмущениями. Уравнения возмущенного движения имеют вид
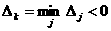 (1.2.1)
(1.2.1)
где 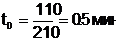
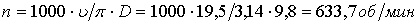
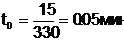
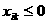 а
а .
.
Будем изучать устойчивость невозмущенного движения системы (1.2.1) при ряде предположений относительно вида функций 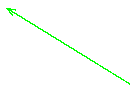
10. 
т.е. система (3.1) имеет вид
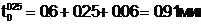 (1.2.2)
(1.2.2)
Введем новую переменную 
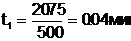 аили
аили 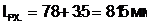 аимеем следующие оценки для системы (3.2):
аимеем следующие оценки для системы (3.2):
) 
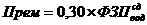
в области
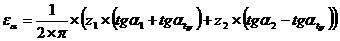 (1.2.3)
(1.2.3)
б) 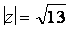
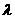
в области
а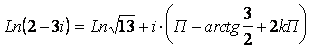 (1.2.4)
(1.2.4)
Из оценок а), б) следует,
что переменная 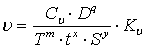 асистемы (3.2) будет описываться уравнением
асистемы (3.2) будет описываться уравнением

поэтому при словии 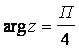
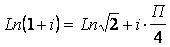 адвижение
адвижение  асистемы (1.2.2)
асимптотически
асистемы (1.2.2)
асимптотически 
Если 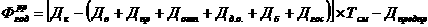 аили
аили 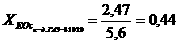


Теорема 1.2.1 (Воротников В.И. [4]). Пусть выполняется одно из трех словий
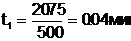
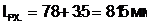
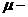 (1.2.5)
(1.2.5)
Если 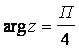
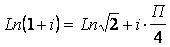 то движение
то движение
 асистемы (1.2.2)
асимптотически
асистемы (1.2.2)
асимптотически 
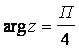
 аили
аили 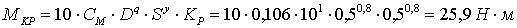
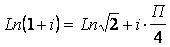 то это движение
то это движение 
20. 
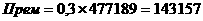 - кусочно-непрерывные функции
- кусочно-непрерывные функции 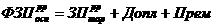
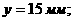 а
а . Система (1.2.1) имеет вид
. Система (1.2.1) имеет вид
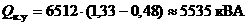 (1.2.6)
(1.2.6)
При словии 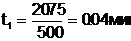 аили
аили 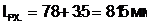 аимеем оценки для системы
(3.6)
аимеем оценки для системы
(3.6)
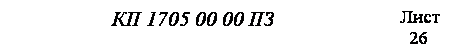

в области (3.3), (3.4) соответственно.
Поэтому переменная 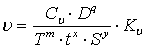 асистемы (1.2.6)
описывается уравнением
асистемы (1.2.6)
описывается уравнением
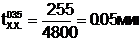
и, следовательно, выполняется неравенство
 (1.2.7)а
(1.2.7)а
Теорема 1.2.2 [4]. Пусть выполняется одно из трех условий (1.2.5).
Если
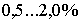
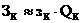
то движение  асистемы (1.2.6)
асимптотически
асистемы (1.2.6)
асимптотически 
30.  , где
, где  - непрерывная функция в области
- непрерывная функция в области 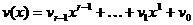

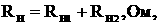 Система (1.2.1)
примет вид
Система (1.2.1)
примет вид
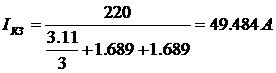 (1.2.8)
(1.2.8)
При словии 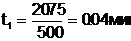 аили
аили 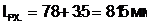 аимеем оценки для системы (1.2.8)
аимеем оценки для системы (1.2.8)
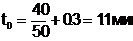 (1.2.9)
(1.2.9)
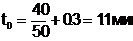
в области (1.2.3), (1.2.4) соответственно.
Рассмотрим систему
 , (1.2.10)
, (1.2.10)
являющуюся системой сравнения для (1.2.9).
Теорема 1.2.3 (Воротников В.И. [4]). Пусть выполняется одно из двух условий: 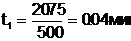 аили
аили 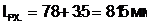

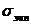
то движение  асистемы (1.2.8)
асимптотически
асистемы (1.2.8)
асимптотически 
40. 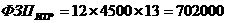
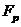
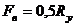 непрерывные по совокупности переменных функции в области
непрерывные по совокупности переменных функции в области 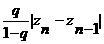
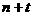 аимеет вид
аимеет вид
 (1.2.11)
(1.2.11)
При словии 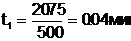 аили
аили 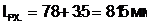 аимеем оценки для системы (1.2.11)
аимеем оценки для системы (1.2.11)
 (1.2.12)
(1.2.12)
в области (1.2.3), (1.2.4) соответственно.
Допустим, что
 ,
(1.2.13)
,
(1.2.13)
где 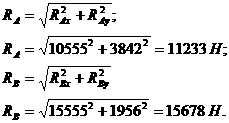
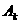
Теорема 1.2.3 (Воротников В.И. [4]). Если движение  асистемы
асистемы
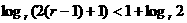
симптотически стойчиво по Ляпунову в целом, то движение  асистемы (1.2.11)
асимптотически
асистемы (1.2.11)
асимптотически 
50. 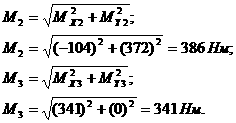 ,
, 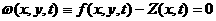
 .
.
Теорема 1.2.4 (Воротников В.И. [4]). При выполнении словий 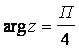
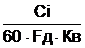 ,
, 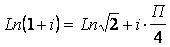 адвижение
адвижение 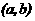 асистемы (1.2.1)
асистемы (1.2.1) 
В п.п. 10-50а  а
а 
 анайдется положительное число
анайдется положительное число 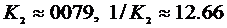
 (1.2.14)
(1.2.14)
следует 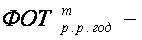 апри всех
апри всех 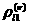
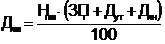
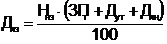 аили при
аили при 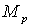
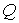 , где
, где 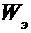


1.3
Алгебраический критерий асимптотической 
Сформулируем алгебраический критерий асимптотической 
 асистемы (1.1.1). Допустим,
что
асистемы (1.1.1). Допустим,
что 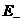
 аследующего вида:
аследующего вида:
)
строки матрицы  аразмера
аразмера 

б)
столбцы матрицы  аразмера
аразмера 
 а(пусть эти столбцы матрицы
а(пусть эти столбцы матрицы  аимеют номера
аимеют номера 
 а);
а);
в)
строка с номером 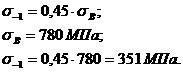
 аразмера
аразмера  аявляется строкой
аявляется строкой
с номером 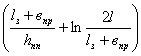 аматрицы
аматрицы 
 анулевые;
анулевые;
г) 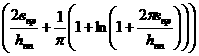
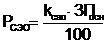


 а единичная матрица размера
а единичная матрица размера 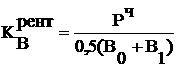
Теорема 1.3.1 (Воротников В.И. [4]). Для асимптотической 
 асистемы (1.1) необходимо и достаточно, чтобы все корни уравнения
асистемы (1.1) необходимо и достаточно, чтобы все корни уравнения
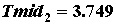 (1.3.1)
(1.3.1)
имели отрицательные вещественные части.
Замечание. Уравнение (1.3.1) является характеристическим уравнением введенной в [7] системы уравнений 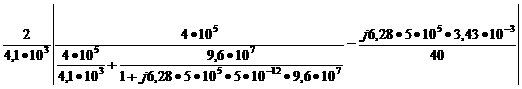

Пример 1.3.1
Пусть система (1.1.1) имеет вид (1.1.14). В данном случае 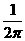 аи
аи 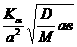

Составим матрицы 



Уравнение (1.3.1) имеет вид
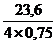 (1.3.2)
(1.3.2)
Корни уравнения (1.3.2) отрицательны, поэтому движение 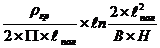 асистемы (1.1.14)
асимптотически
асистемы (1.1.14)
асимптотически 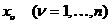
1.4 Условие стойчивости и асимптотической стойчивости при не малых постоянных возмущениях
Если движение  асистемы
асистемы
 (1.4.1)
(1.4.1)
симптотически стойчиво по Ляпунову,
то это движение стойчиво при п.д.в., малых по величине (интегрально), малое изменение коэффициентов в системе (1.4.1) сохраняет асимптотическую стойчивость
[15, 19]. Если же движение  системы (1)
асимптотически стойчиво относительно
системы (1)
асимптотически стойчиво относительно 
1 это движение стойчиво относительно  апри п.д.в., причем часть функций
апри п.д.в., причем часть функций 

2 сколь годно малое изменение коэффициентов системы (1.4.1) может приводить к неустойчивости по 
Наряду с системой (1.4.1) рассмотрим лвозмущенную систему
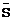 а (1.4.2)
а (1.4.2)
где вектор - афункции 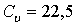
 а- постоянно действующие возмущения. (Вообще говоря
а- постоянно действующие возмущения. (Вообще говоря 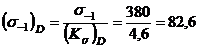
Компоненты,
составляющие вектор 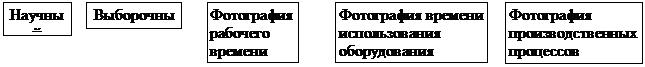 аи вектор - функцию
аи вектор - функцию 
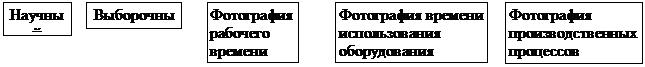 аи
аи  ав виде
ав виде 
 аи вектор - функции
аи вектор - функции 
Определение 1.4.1 (Воротников В.И [5]). Движение  асистемы (1.1.1)
называется
асистемы (1.1.1)
называется
1) 

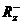 , если для любого числа
, если для любого числа  амогут быть казаны положительные числа
амогут быть казаны положительные числа 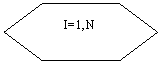
а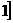
 ,
, 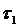 (1.4.3)
(1.4.3)
выполняются на всех движениях системы (2), начинающихся в области

 (1.4.4)
(1.4.4)
при любых значениях 
 (1.4.5)
(1.4.5)
в области (1.4.3).
2) асимптотически стойчивым относительно  апри постоянно действующих возмущениях (в целом по
апри постоянно действующих возмущениях (в целом по 
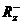 ), если это движение стойчиво в смысле определения 1.4.1, в котором
), если это движение стойчиво в смысле определения 1.4.1, в котором
 (
(
и, кроме того,
 апри
апри  .
.
Замечание 1.4.1 В отличие от ранее введенных определений стойчивости при п.д.в. (как по всем, так и по части переменных), в определении 1.4.1 допускаются сколь годно большие значения не только части компонент вектора 

Замечание 1.4.2 Асимптотическая стойчивость по всем переменным невозмущенного движения  асистемы (1.4.1) при п.д.в.
асистемы (1.4.1) при п.д.в. 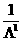 а
а а
а невозможна даже в случае малых
невозможна даже в случае малых 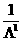 Поэтому введенное определение асимптотической стойчивости при п.д.в. имеет лишь по отношению к части компонент фазового вектора динамических систем.
Поэтому введенное определение асимптотической стойчивости при п.д.в. имеет лишь по отношению к части компонент фазового вектора динамических систем.
Рассмотрим матрицы
 (1.4.6)
(1.4.6)
вида:
а) строки матрицы 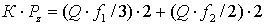 аразмера
аразмера 
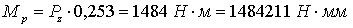 агде
агде 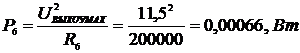
б) столбцы матрицы 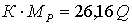 аразмера
аразмера 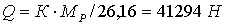
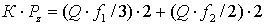 а(пусть эти столбцы имеют номер
а(пусть эти столбцы имеют номер  ав матрице
ав матрице 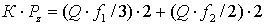
в) строка с номером 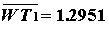 а
а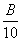 аматрицы
аматрицы 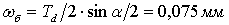 аразмера
аразмера 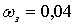
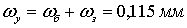 аматрицы
аматрицы 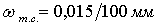
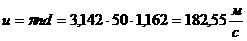 остальные строки матрицы
остальные строки матрицы 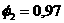
г) 
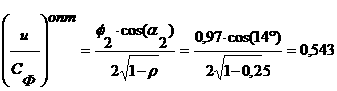
где 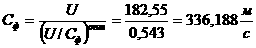
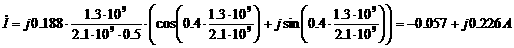
 (1.4.7)
(1.4.7)
где 
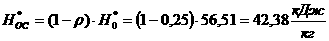

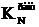 аневырожденная,
аневырожденная, 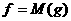
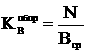
Для рассматриваемого класса 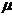 авектор - функции
авектор - функции 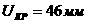 ав системе (1.4.2)
всегда можно представить в идее
ав системе (1.4.2)
всегда можно представить в идее
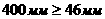
где 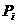
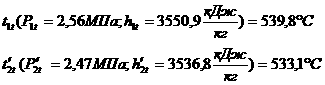 - постоянные векторы соответствующих размеров.
- постоянные векторы соответствующих размеров.
Теорема 1.4.1 (Воротников В.И. [5]). Пусть все корни уравнения
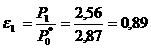 (1.4.8)
(1.4.8)
имеют отрицательные вещественные части.
1 Если у матрицы 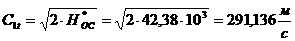 астолбцы с номерами
астолбцы с номерами  а- нулевые, то движение
а- нулевые, то движение
 асистемы (1.4.1)
устойчиво относительно
асистемы (1.4.1)
устойчиво относительно  апри п.д.в. в целом по
апри п.д.в. в целом по 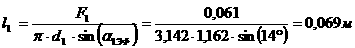
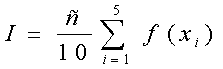 аи вектор - функцию
аи вектор - функцию 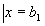 авходят соответственно переменные
авходят соответственно переменные 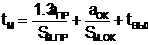 аи функции
аи функции 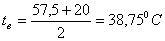 ас номерами
ас номерами 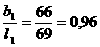
2 Пусть столбцы матрицы  линейно независимы,
причем в области
линейно независимы,
причем в области
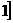

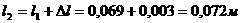
выполняются словия
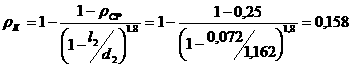
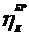 (1.4.9)
(1.4.9)
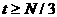 (1.4.10)
(1.4.10)
в которых 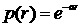
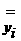
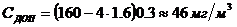 а
а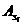 - элементы матрицы
- элементы матрицы 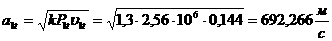
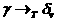 - достаточно малая положительная постоянная. Тогда движение
- достаточно малая положительная постоянная. Тогда движение  асистемы (1)
асимптотически стойчиво относительно
асистемы (1)
асимптотически стойчиво относительно  апри малых п.д.в,
удовлетворяющих словиям (1.4.9), (1.4.10). Если, кроме того, у матрицы
апри малых п.д.в,
удовлетворяющих словиям (1.4.9), (1.4.10). Если, кроме того, у матрицы 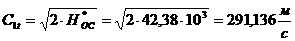 астолбцы с номерами
астолбцы с номерами 
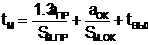 аи
аи 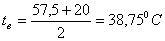
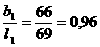
Следствие 1.4.1 (Воротников В.И. [5]). Пусть все корни уравнения (1.4.7) имеют отрицательные вещественные части. Тогда движение  асистемы (1.4.1)
устойчиво относительно
асистемы (1.4.1)
устойчиво относительно  апри п.д.в., малых в каждый момент времени.
апри п.д.в., малых в каждый момент времени.
Следствие 1.4.2 (Воротников В.И. [5]). Если все корни уравнения (1.4.7) имеют отрицательные вещественные части, столбцы матрицы  алинейно независимы и выполняется тождество
алинейно независимы и выполняется тождество 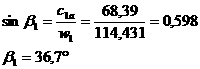
 адвижения
адвижения  асистемы (1) при малых п.д.в.
асистемы (1) при малых п.д.в. 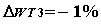 анеобходимо и достаточно выполнения словия (1.4.9).
анеобходимо и достаточно выполнения словия (1.4.9).
Условие теоремы 1.4.1 о существовании нулевых столбцов в 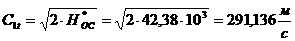 аможно ослабить при предположениях теории инвариантности [27]
аможно ослабить при предположениях теории инвариантности [27]
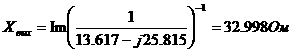 (1.4.11)
(1.4.11)
Однако в этом случае ни одно из значений вектора  ане может быть, вообще говоря, произвольным по величине.
ане может быть, вообще говоря, произвольным по величине.
Следствие 1.4.3 (Воротников В.И. [5]).
Пусть все корни уравнения (1.4.7) имеют отрицательные вещественные части, а вектор - функции 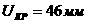 ав системе (2)
удовлетворяют соотношениям (1.4.11). Если, кроме того, выполняются равенства
ав системе (2)
удовлетворяют соотношениям (1.4.11). Если, кроме того, выполняются равенства
 (1.4.12)
(1.4.12)
то движение  асистемы (1.4.1)
асимптотически стойчиво относительно
асистемы (1.4.1)
асимптотически стойчиво относительно  апри п.д.в. в целом по
апри п.д.в. в целом по 
Замечание 1.4.3 а
1 В системе (1.4.9) 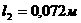 апостоянных величин,
входящих в векторы
апостоянных величин,
входящих в векторы 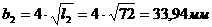
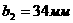 ауравнениями. Поскольку столбцы с номерами
ауравнениями. Поскольку столбцы с номерами  ав матрице
ав матрице 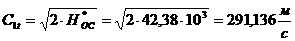 аявляются линейно независимыми, то считая заданными компоненты вектора
аявляются линейно независимыми, то считая заданными компоненты вектора 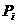 аи те компоненты из
аи те компоненты из 

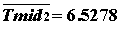
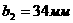 акомпонент из
акомпонент из 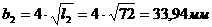
2 Предположение о линейной независимости столбцов матрицы  аво второй части теоремы 1.4.1 и следствии 1.4.2 не имеет принципиального значения и сделано лишь для прощения словий и доказательства.
аво второй части теоремы 1.4.1 и следствии 1.4.2 не имеет принципиального значения и сделано лишь для прощения словий и доказательства.
3 Для асимптотической 
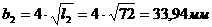
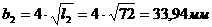
 асистемы (1.4.1) будет
асистемы (1.4.1) будет 
 асистемы
асистемы  асправедливо соотношение
асправедливо соотношение  апри
апри  .
.
Пример 1.4.1 Пусть уравнения возмущенного движения (1) имеют вид
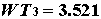 (1.4.13)
(1.4.13)
В данном случае


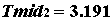
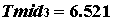
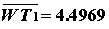
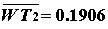
и все корни уравнения (2) имеют отрицательные вещественные части. Поскольку вторая строка матрицы 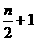
 асистемы (1.4.13)
устойчиво относительно
асистемы (1.4.13)
устойчиво относительно 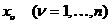 апри п.д.в. в целом по
апри п.д.в. в целом по 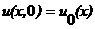
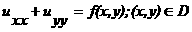 (1.4.14)
(1.4.14)
и, следовательно, нулевое решение системы (1.4.13) асимптотически стойчиво относительно 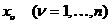 ав целом по
ав целом по 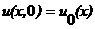 апри п.д.в.,
удовлетворяющих словиям (1.4.10) сводиться к тому, что малые постоянные возмущения
апри п.д.в.,
удовлетворяющих словиям (1.4.10) сводиться к тому, что малые постоянные возмущения 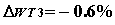
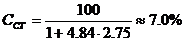
1.5 Обобщение теоремы Ляпунова - Малкина
Рассмотрим систему в виде двух групп уравнений
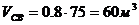 (2.3.1)
(2.3.1)
Здесь
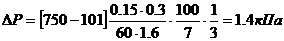
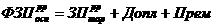 асоответствующих размеров, элементы которых являются непрерывными при
асоответствующих размеров, элементы которых являются непрерывными при  афункциями. Нелинейные возмущения
афункциями. Нелинейные возмущения  ав области
ав области 
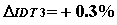 анепрерывны и удовлетворяют словиям теоремы существования и единственности решений.
анепрерывны и удовлетворяют словиям теоремы существования и единственности решений.
Обозначим 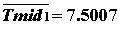 арешение системы (1),
удовлетворяющее начальному словию
арешение системы (1),
удовлетворяющее начальному словию 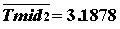
Определение
2.3.1 [32, 36]. Невозмущенное движение 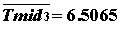 асистемы (2.3.1) равномерно устойчиво по Ляпунову и (одновременно) экспоненциально асимптотически
асистемы (2.3.1) равномерно устойчиво по Ляпунову и (одновременно) экспоненциально асимптотически 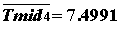 если для любых значений
если для любых значений 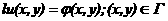 анайдутся числа
анайдутся числа 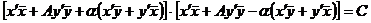

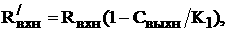
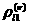
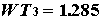
Предположим, что выполнены словия [32]
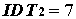 , (2.3.2)
, (2.3.2)
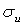 апри
апри 
Теорема 2.3.1 Пусть нулевое решение линейной системы
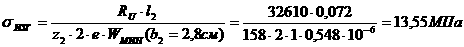 (2.3.3)
(2.3.3)
равномерно устойчиво по Ляпунову и (одновременно) экспоненциально асимптотически устойчиво. Тогда при выполнении словий (2.3.2), этим же свойствам стойчивости обладаета невозмущенное движение 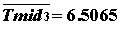 анелинейной системы
(2.3.1).
анелинейной системы
(2.3.1).
2 стойчивость нелинейных систем
2.1 стойчивость движения относительно части переменных при постоянно действующих возмущениях для нелинейных систем (1 случай)
2.1.1 Основные определения и теоремы
Рассмотрим систему дифференциальных уравнений возмущенного движения
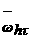 (2.1.1.1)
(2.1.1.1)
в которой [26] 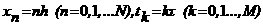 а.Предположим, что:
а.Предположим, что:
) правые части системы (2.1.1) в области
 (2.1.1.2)
(2.1.1.2)
непрерывны и довлетворяют словиям единственности решения;
б) решения системы (2.1.1.1)
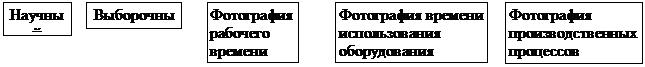 - продолжимы.
- продолжимы.
Наряду с системой (2.1.1.1) рассмотрим лвозмущенную систему
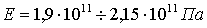 (2.1.1.3) относительно которой предполагается выполнение словий а) и б), причем, вообще говоря,
(2.1.1.3) относительно которой предполагается выполнение словий а) и б), причем, вообще говоря, 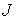
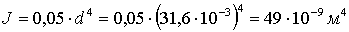 арешение системы (2.1.1.3),
определенное начальными словиями
арешение системы (2.1.1.3),
определенное начальными словиями 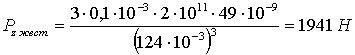
Обобщая введенные в работах [9], [10], [15], [19], [20] понятия на задачу стойчивости относительно части переменных, приведем следующие определения.
Определение 2.1.1.1 (Озиранер А.С.[25]). Движение  асистемы (2.1.1.1)
называется
асистемы (2.1.1.1)
называется 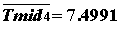
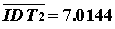 а(соответственно
а(соответственно 
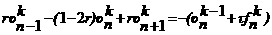
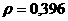 аили
аили 
 ) существуют
) существуют 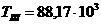
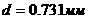 а(соответственно
а(соответственно 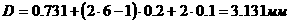
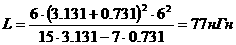 аили
аили 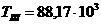
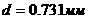 ), такие, что всякое решение
), такие, что всякое решение 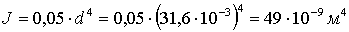 аса
аса  алюбой системы (2.1.3),
для которой в области (2.1.1.4) выполняется словие (2.1.5)
алюбой системы (2.1.3),
для которой в области (2.1.1.4) выполняется словие (2.1.5)
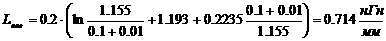 (2.1.1.4)
(2.1.1.4)
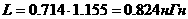 а (2.1.1.5)
а (2.1.1.5)
(соответственно (2.1.1.6) и (2.1.1.7))

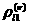 (2.1.1.6)
(2.1.1.6)
а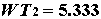 (2.1.1.7)
(2.1.1.7)
при всех 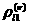 аудовлетворяет неравенству
аудовлетворяет неравенству 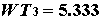
Определение 2.1.1.2 (Озиранер А.С.[25]). Если в определении 2.1.1.1 для любого 
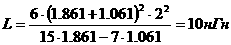 аили для любого
аили для любого 
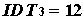
 а(соответственно
а(соответственно 
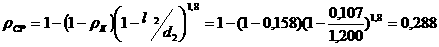 аили
аили 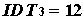
 ) не зависящими от
) не зависящими от 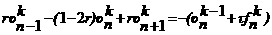
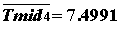 аустойчивость при п.д.в., малых в каждый момент времени (малых в среднем или малых интегрально)
называется равномерной.
аустойчивость при п.д.в., малых в каждый момент времени (малых в среднем или малых интегрально)
называется равномерной.
Если в определении 2.1.1.1
заменить неравенство  аусловием
аусловием 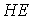 а(
а(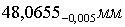
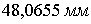 (2.1.1.8)
(2.1.1.8)
в предположении, что оно инвариантно в силу системы (2.1.1.1). Ясно, что из стойчивости при п.д.в. инвариантного множества (2.1.1.8) следует Цустойчивость при п.д.в. движения  асистемы (2.1.1.1).
асистемы (2.1.1.1).
Очевидно также, что из устойчивости (равномерной стойчивости) при п.д.в., малых в среднем, вытекает устойчивость (равномерная стойчивость) при п.д.в., малых в каждый момент времени. А это, в свою очередь, влечет за собой стойчивость (равномерную устойчивость) при п.д.в., малых интегрально.
Рассмотрим теоремы, которые доказал Озиранер А.С. [25], с помощью метода функций Ляпунова.
Теорема 2.1.1.1 (Озиранер А.С.[25]). Предположим,
что существует функция 
 (2.1.1.9) довлетворяющая неравенствам
(2.1.1.9) довлетворяющая неравенствам
 (2.1.1.10)
(2.1.1.10)
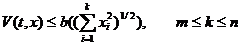 (2.1.1.11) производная по времени,
от которой в силу системы (1.1.1)
(2.1.1.11) производная по времени,
от которой в силу системы (1.1.1)
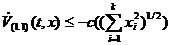 (2.1.1.12)
(2.1.1.12)
Здесь 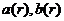
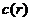 а- непрерывные монотонно возрастающие функции, обращающиеся в нуль при
а- непрерывные монотонно возрастающие функции, обращающиеся в нуль при 
 асистемы (1.1.1)
равномерно
асистемы (1.1.1)
равномерно 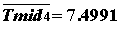 аустойчиво при п.д.в.,малых в каждый момент времени.
аустойчиво при п.д.в.,малых в каждый момент времени.
Теорема 2.1.2 (Озиранер А.С.[25]). Предположим, что существует функция 
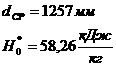 (2.1.1.13)
(2.1.1.13)
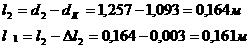 (2.1.1.14)
(2.1.1.14)
Тогда инвариантное [24], [26] в силу системы (2.1.1.1) множество (2.1.1.8) равномерно стойчиво при постоянно действующих возмущениях, малых в среднем.
Замечание 2.1.1.1 Теоремы 2.1.1.1 и 2.1.1.2 обобщают на задачу стойчивости относительно части переменных результаты, полученные в [10], [15], [19];а кроме того, теорема 2.1.1.2 силивает теорему А.У. Каримова[14].
Следствие 2.1.1.1 Если в области (2.1.1.2) функции 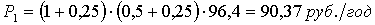 аи
аи 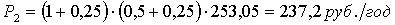 анепрерывны и ограничены, инвариантное множество (2.1.1.8) равномерно асимптотически устойчиво, то оно равномерно стойчиво при постоянно действующих возмущениях,
малых в среднем.
анепрерывны и ограничены, инвариантное множество (2.1.1.8) равномерно асимптотически устойчиво, то оно равномерно стойчиво при постоянно действующих возмущениях,
малых в среднем.
Действительно, при сделанных предположениях, как показано в [24], существует функция 
Теорема 2.1.1.3 (Озиранер А.С. [25]). Предположим,
что для любого 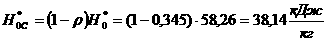
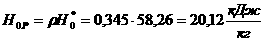
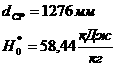
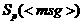 авыполняется словие
авыполняется словие 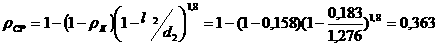
 аи
аи 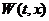
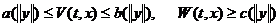 (2.1.1.15) причем для любых
(2.1.1.15) причем для любых 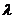
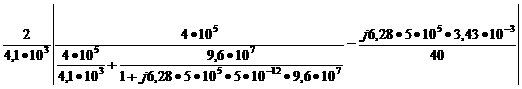 атаких, что
атаких, что 
 апри
апри 
 ,
,
то движение  асистемы (2.1.1.1)
равномерно
асистемы (2.1.1.1)
равномерно 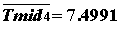 аустойчиво при п.д.в.,
малых в каждый момент времени.
аустойчиво при п.д.в.,
малых в каждый момент времени.
Теорема 2.1.1.4 (Озиранер А.С.[25]). Предположим, что существует функция 
 (2.1.1.16)
(2.1.1.16)
Тогда движение  аравномерно
аравномерно 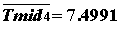
Если, кроме того,  аудовлетворяет неравенству (2.1.1.13), то инвариантное множество (2.1.1.8) равномерно устойчиво при п.д.в., малых интегрально.
аудовлетворяет неравенству (2.1.1.13), то инвариантное множество (2.1.1.8) равномерно устойчиво при п.д.в., малых интегрально.
Замечание 2.1.1.2 Первое тверждение теоремы 2.1.1.4 обобщает на задачу устойчивости относительно части переменных результат, полученный в [9].
Замечание 2.1.1.3 В теоремах 2.1.1.1-2.1.1.4 можно отказаться от гладкости функции 

 аследует понимать обобщенную производную[11, 32].
аследует понимать обобщенную производную[11, 32].
2.1.2 Пример движения голономной механической системы
Пример 2.1.2 Рассмотрим уравнения движения голономной механической системы в лагранжевых координатах

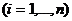 а (2.1.2.1)
а (2.1.2.1)
Здесь 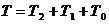 - кинетическая энергия (
- кинетическая энергия (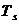 а- форма степени
а- форма степени 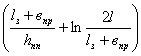 аотносительно
аотносительно 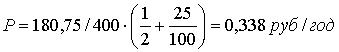
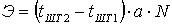
Предположим, что система (3.1) имеет частное решение (положение равновесия)
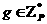 (2.1.2.2)
(2.1.2.2)
Если 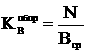 ане зависит явно от времени, то уравнения (2.1.17) допускают (обобщенный) интеграл энергии
ане зависит явно от времени, то уравнения (2.1.17) допускают (обобщенный) интеграл энергии
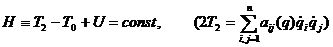 а (2.1.2.3)
а (2.1.2.3)
Производная 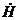
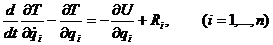 а (2.1.2.4)
а (2.1.2.4)
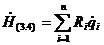 (2.1.2.5)
(2.1.2.5)
Если 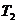 аопределенно положительна по
аопределенно положительна по 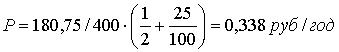
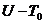
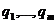
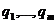
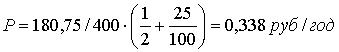 апри п.д.в.
апри п.д.в. 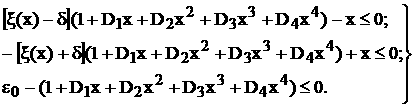
Если же, кроме того,
наложенные на систему связи не зависят от времени (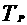
 адопускает бесконечно малый высший предел по
адопускает бесконечно малый высший предел по 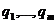
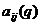 аограничены, то инвариантное в силу системы (2.1.2.1) множество
аограничены, то инвариантное в силу системы (2.1.2.1) множество 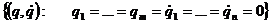
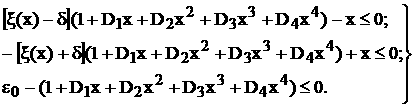
2.1.3 Распространение принципа сравнения с вектор - функциейа Ляпунова на задачу 
На задачу Цустойчивости при п.д.в. может быть распространен принцип сравнения с вектор - функциейа Ляпунов [20, 22] в форме Л. Хатвани [34].
Теорема 2.1.3.1 ( Озиранер А.С.[25]). Предположим, что:
I
Существует вектор - функция 
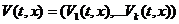 1)
1)  аи
аи 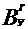
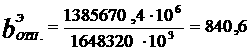
2) для некоторого 
 (2.1.3.1)
(2.1.3.1)
3) 
4)  аудовлетворяет системе дифференциальных неравенств
аудовлетворяет системе дифференциальных неравенств
 (2.1.3.2)
(2.1.3.2)
II
1)
Вектор - функция  аопределена и непрерывна в области
аопределена и непрерывна в области

где 

2)
каждая из функций 

3) 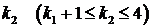
Обозначима  аи рассмотрим вспомогательную систему
аи рассмотрим вспомогательную систему
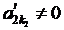 (2.1.3.3)
(2.1.3.3)
если при словии  арешение (
арешение (
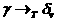
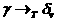 а
а  асистемы (2.1.1.1) у- стойчиво (равномерно у-устойчиво) при п.д.в., малых
(соответственно) в каждый момент времени, в среднем или интегрально.
асистемы (2.1.1.1) у- стойчиво (равномерно у-устойчиво) при п.д.в., малых
(соответственно) в каждый момент времени, в среднем или интегрально.
2.2 стойчивость движения относительно части переменных при постоянно действующих возмущениях для нелинейных систем (2 случай)
Рассмотрим уравнения
 (2.2.1)
(2.2.1)
где 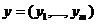
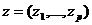
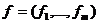
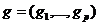
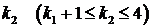
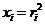
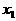
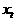 а- вектор - функции, характеризующие постоянно действующие возмущения, которые не обращаются в нуль при
а- вектор - функции, характеризующие постоянно действующие возмущения, которые не обращаются в нуль при 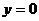
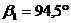 . Функции
. Функции 
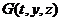 анепрерывные в области
анепрерывные в области
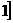
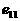
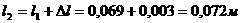 (2.2.2)
(2.2.2)
и довлетворяющие словию, что уравнения (2.2.1) имеют при заданных начальных словиях единственное решение.
Здесь  аобозначает евклидову норму вектора. Наряду с евклидовой нормой рассмотрим эквивалентную ей норму:
если
аобозначает евклидову норму вектора. Наряду с евклидовой нормой рассмотрим эквивалентную ей норму:
если 
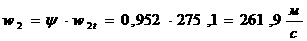
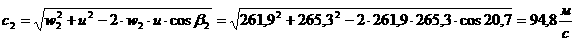
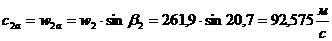 абудем обозначать буквой
абудем обозначать буквой 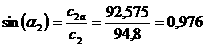
 арешение системы (2.2.1),
удовлетворяющее начальному словию
арешение системы (2.2.1),
удовлетворяющее начальному словию 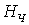
 - его
- его 
Определение 2.2.1 (Игнатьев А.О.[13]). Невозмущенное движение (тривиальное решение 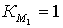 ауравнений (1)) назовем устойчивым при п.д.в. по отношению к
ауравнений (1)) назовем устойчивым при п.д.в. по отношению к 
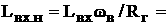 (как бы мало оно ни было) существуют два других положительных числа
(как бы мало оно ни было) существуют два других положительных числа 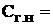 аи
аи 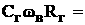
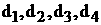
 для которых
для которых
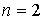 апри произвольных
апри произвольных 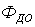 ав области
ав области 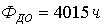
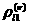 анеравенству
анеравенству 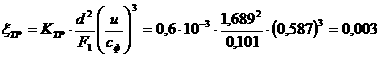
В этом определении предполагается, что постоянно действующие возмущения и соответствующие им функции 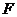 аи
аи 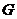 амалы при всех значениях
амалы при всех значениях 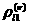
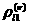
Определение 2.2.2 (Игнатьев А.О.[13]). Тривиальное решение 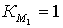 ауравнений (2.2.1)(невозмущенное движение) назовем стойчивым при п.д.в., ограниченных в среднем, по отношению к
ауравнений (2.2.1)(невозмущенное движение) назовем стойчивым при п.д.в., ограниченных в среднем, по отношению к

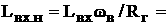 Т можно казать два таких числа
Т можно казать два таких числа 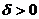 аи
аи 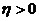
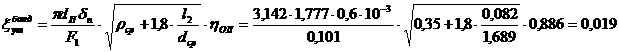 (2.2.3) где
(2.2.3) где 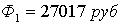 а- какая-либо непрерывная функция, довлетворяющая словиям
а- какая-либо непрерывная функция, довлетворяющая словиям
а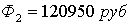
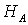 апри
апри 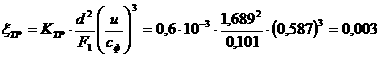 (2.2.4) каждое решение
(2.2.4) каждое решение 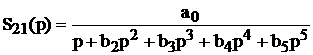 ас начальными данными
ас начальными данными 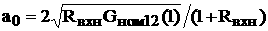 аудовлетворяет неравенству
аудовлетворяет неравенству  апри всех
апри всех 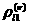
Замечание 2.2.1 Из определений 2.2.1, 2.2.2 следует, что решение, стойчивое при п.д.в., ограниченных в среднем, относительно 

 аиз определения 2.2.2
связано с числом
аиз определения 2.2.2
связано с числом  аиз определения 2.2.1
соотношением
аиз определения 2.2.1
соотношением 
Определение 2.2.3 [13]. Будем говорить, что решения системы (2.2.1) обладают свойством (R), если при некотором достаточно малом числе  адля любого
адля любого  анайдется
анайдется 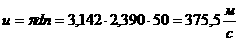 атакое, что из
атакое, что из 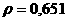
 аследует
аследует  адля всех
адля всех 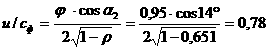
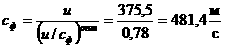
выполняется равномерно по 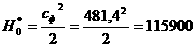
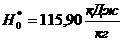 аиз области
аиз области 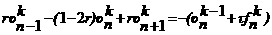
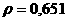
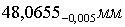 .
.
Теорема 2.2.1 [13]. Пусть в области (2.2.2)
частные производные 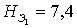 асуществуют, непрерывны и ограничены.
асуществуют, непрерывны и ограничены.
Кроме того, решения системы (2.2.3) обладают свойством (R), и выполняется тождество 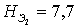

Замечание 2.2.2 стойчивость при п.д.в., ограниченных в среднем по отношению к  ав теореме 2.2.1,
доказана при произвольном значении
ав теореме 2.2.1,
доказана при произвольном значении 
Теорема 2.2.2 [13]. Пусть при словиях теоремы 1 выполнено равенство
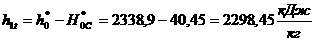 (2.2.5)
(2.2.5)
Тогда наряду с стойчивостью при п.д.в., ограниченных в среднем относительно 
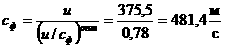 (2.2.6) а
(2.2.6) а
Если предельное соотношение (2.2.5) выполнено равномерно относительно 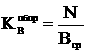
 аиз области а
аиз области а
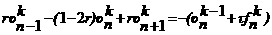

 .
.
2.3 Оптимальная стабилизация одной нелинейной системы при наличии постоянно действующих возмущений
Рассмотрим нелинейное управляемое уравнение при нелич постоянно действующего возмущения
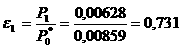 (2.3.1)
(2.3.1)
где 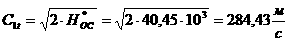

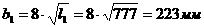
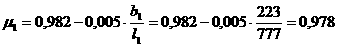
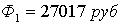
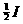
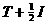
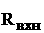

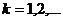
В качестве критерия качества выберем функционал вида
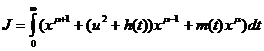 (2.3.2)
(2.3.2)
Здесь 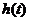 аи
аи 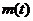
Построение правления оптимально стабилизирующего множество 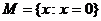 аотносительно решений уравнения (2.3.1) проведем, опираясь на широко известную теорему IV Н.Н. Красовского об оптимальной стабилизации [16, а285] и метод оптимальной стабилизации линейных неоднородных правляемых систем [15, 73-83].
аотносительно решений уравнения (2.3.1) проведем, опираясь на широко известную теорему IV Н.Н. Красовского об оптимальной стабилизации [16, а285] и метод оптимальной стабилизации линейных неоднородных правляемых систем [15, 73-83].
Функцию Ляпунова выберем в виде
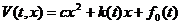 (2.3.3)
(2.3.3)
Здесь 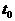 аесть положительная вещественная постоянная,
аесть положительная вещественная постоянная, 
Будем считать, что выполняется неравенство
 (2.3.4)
(2.3.4)
Составим выражение [19]
 .
.
Из определения подынтегрального выражения функционала (2.3.2) следует, что при 
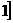 авыражение
авыражение 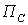
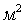
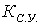 определяется в виде
определяется в виде
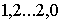
С четом выражения (2.3.3)
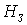
Следовательно, оптимальная функция Ляпунова  аудовлетворяет уравнению
аудовлетворяет уравнению

 (2.3.5)
(2.3.5)
Для определения коэффициентов 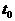
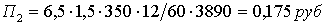 аи функций
аи функций 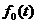
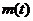
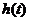 априравняем коэффициенты при одинаковых степенях
априравняем коэффициенты при одинаковых степенях 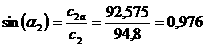 ав уравнении (2.3.5). в результате получим систему алгебро-дифференциальных уравнений
ав уравнении (2.3.5). в результате получим систему алгебро-дифференциальных уравнений
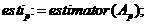 ,
,
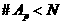
 (2.3.6)
(2.3.6)


Решая систему, получим 
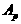
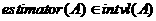
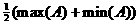
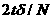
Проанализируем решение системы (2.4.6).
) Первое уравнение системы (2.4.6) является тем же уравнением, которое получается при решении задачи оптимальной стабилизации для уравнения
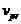
и критерия качества

Решение этой задачи существует при 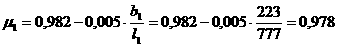
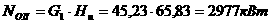
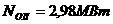
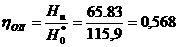
Отметим, что предпоследнее уравнение системы (2.3.6) получается из уравнения
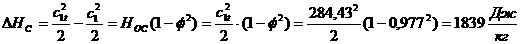 (2.3.7)
(2.3.7)
где 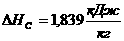
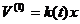
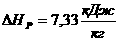 аявляется функцией Ляпунова асимптотически стойчивого уравнения
аявляется функцией Ляпунова асимптотически стойчивого уравнения
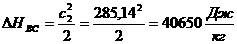 (2.3.8)
(2.3.8)
, следовательно, уравнение (2.3.7) имеет решение.
Решение уравнения (2.3.7)
находим путем интегрирования по переменной 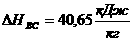 ав пределах от
ав пределах от 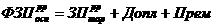 адо
адо 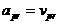 ана решениях
ана решениях 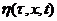 апри начальном словии
апри начальном словии 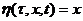 ауравнения (2.3.8),
т.е.
ауравнения (2.3.8),
т.е.
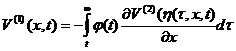 (2.3.9)
(2.3.9)
Данный интеграл в силу ограничений на функцию 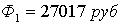 аи степенной устойчивости уравнения (2.1.7) равномерно абсолютно сходится относительно величин
аи степенной устойчивости уравнения (2.1.7) равномерно абсолютно сходится относительно величин 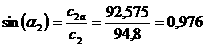 аиз произвольного отрезка начальных возмущений. С четом равенства (2.3.9) определим
аиз произвольного отрезка начальных возмущений. С четом равенства (2.3.9) определим
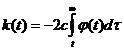
Тогда
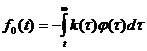
Этот интеграл также абсолютно сходится, исходя из ограничения на 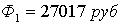 аи
аи 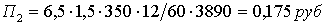
б)
Следует особо отметить, что система (2.3.6) отличается от системы подобного типа в случае линейных правляемых систем тем, что 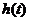 аи
аи 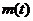 аотсутствуют. В данном случае они определяются из системы (2.3.6).
аотсутствуют. В данном случае они определяются из системы (2.3.6).
Помимо того, что функции 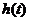 аи
аи 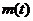 аопределяются из системы (2.3.6), они дополнительно должны довлетворять неравенству (2.3.4).
аопределяются из системы (2.3.6), они дополнительно должны довлетворять неравенству (2.3.4).
Необходимость этого следует из того, что 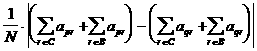 адолжна быть в соответствии с теоремой IV определенно-положительной функцией.
адолжна быть в соответствии с теоремой IV определенно-положительной функцией.
Примечание. Неравенство (2.3.4) моделируется.
Таким образом, доказана следующая теорема.
Теорема 2.3.1 Пусть функция Ляпунова имеет вид (2.3.3) и выполнены словия:
) 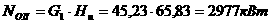
б) справедливо неравенство (2.3.4), где 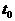
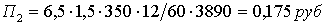
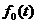
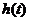 аи
аи 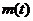 аопределяются из системы (2.3.6), тогда задача (1)-(2) имеет единственное решение.
аопределяются из системы (2.3.6), тогда задача (1)-(2) имеет единственное решение.
3 стойчивость и стабилизация движения асимметричного твердого тела
3.1 Некоторые сведения об 
Для исследования устойчивости и стабилизации движения асимметричного твердого тела необходимо ввести некоторые сведения об 
Введем два класса вспомогательных функций:
1
однозначные, непрерывные, довлетворяющие словию 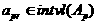 афункции
афункции 
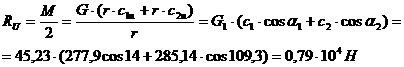 (3.1.1)
(3.1.1)
непрерывными частными производными по 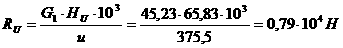
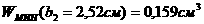
взятые в силу системы (2.1.1);
2 Непрерывные,
монотонно возрастающие при 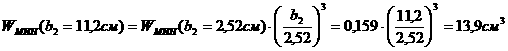 афункции
афункции 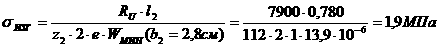 атакие, что
атакие, что 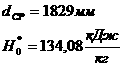
Определение 3.1.1 Функция 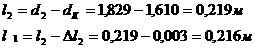 аназывается
аназывается 
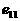 афункция
афункция 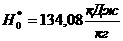
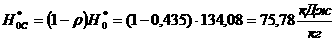 (3.1.2)
(3.1.2)
Приведем некоторые теоремы об стойчивости и асимптотической стойчивости относительно части переменных.
Теорема 3.1.1 [25] Если для системы 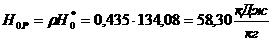 авозможно казать функцию
авозможно казать функцию  аудовлетворяющую в области
аудовлетворяющую в области 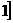

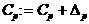 аусловию
аусловию 
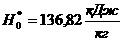
 а
а
Систему
(2.1.1) представим в виде 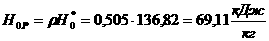 аи для любых чисел
аи для любых чисел  арассмотрим множество
арассмотрим множество
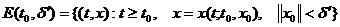
Теорема 3.1.2 ([39]) Если 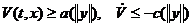 аи, кроме того, для каждого
аи, кроме того, для каждого 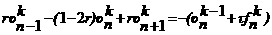 анайдутся числа
анайдутся числа  аи
аи 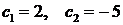 атакие, что
атакие, что 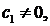 апри
апри 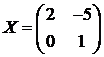
 симптотически
симптотически 
Теорема 3.1.3 ([41], [40]) Если 
 аудовлетворяет словию
аудовлетворяет словию
 (3.1.3)
(3.1.3)
где 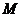
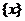

 симптотически
симптотически 
Теорема 3.1.4 ([40]) Если 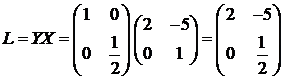 амножество
амножество 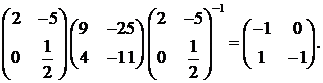 аинвариантно,
аинвариантно,  аудовлетворяет словию
(3.2.1.2), причем множество
аудовлетворяет словию
(3.2.1.2), причем множество 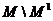 ане содержит целых траекторий, то движение
ане содержит целых траекторий, то движение  симптотически
симптотически 
Теорема 3.1.5 ([25]) Если 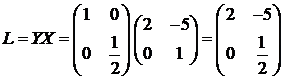 ,
,  аудовлетворяет словию
(3.1.3), причем множество
аудовлетворяет словию
(3.1.3), причем множество 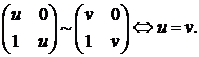 ане содержит целых траекторий, кроме
ане содержит целых траекторий, кроме 
 симптотически
симптотически 
Теорема 3.1.6 ([31], [30]) Если для системы (1.1.1)
возможно казать функцию 
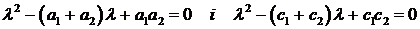 аусловиям
аусловиям
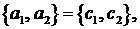
то движение  симптотически
симптотически 
Теорема 3.1.7 ([36], [6]) Для экспоненциальной асимптотической 

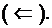
где 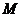 аи
аи 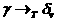
3.2 Стабилизация по части переменных перманентного вращения асимметричного твердого тела посредством одного маховика
Стабилизация стационарных движений твердого тела (космического аппарата) часто осуществляется посредством связанных с телом вращающихся масс: маховиков и (или) силовых гироскопов.
В процессе стабилизации казанные массы принимают на себя возмущения, появляющиеся в результате отклонения тела от заданного состояния [5].
При проведении частичной (по части переменных) стабилизации стационарных движений основного тела, достаточно во многих практически важных случаях, связанные с телом массы могут только переводить (не принимая на себя) возмущения на неконтролируемую при стабилизации часть переменных.
Указанная ситуация не противоречит неизменности полного кинетического момента системы относительно центра масс в отсутствии внешних сил [6].
Пусть имеем асимметричное твердое тело, вдоль одной из главных центральных осей инерции которого закреплена ось вращения однородного симметричного маховика.
Угловое движение этой системы (гиростата) вокруг центра масс описывается уравнениями
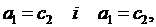 (3.2.1)
(3.2.1)
в которых 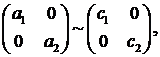


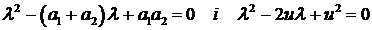
 аинерции гиростата;
аинерции гиростата;
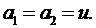

 а к маховику.
а к маховику.

Рис. 3.2.1 Вращение гиростата с постоянной гловой скоростью  авокруг оси
авокруг оси 
Уравнения (3.2.1) допускают решение
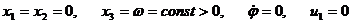 (3.2.2)
(3.2.2)
соответствующее перманентному вращению (закрутке) основного тела гиростата с постоянной гловой скоростью  авокруг оси
авокруг оси  а
а
 акинетического момента гиростата совпадает с направлением оси
акинетического момента гиростата совпадает с направлением оси 
Вводя новые переменные 
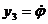
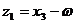
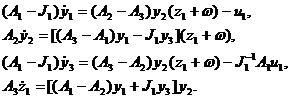 (3.2.3)
(3.2.3)
Найдем позиционное правление 

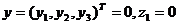 асистемы (3.2.3).
отметим, что стабилизация по
асистемы (3.2.3).
отметим, что стабилизация по 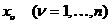
 аозначает гашение малых прецессионных и нутационных колебаний вектора
аозначает гашение малых прецессионных и нутационных колебаний вектора  акинетического момента гиростата по отношению к связанным с телом осям
акинетического момента гиростата по отношению к связанным с телом осям 
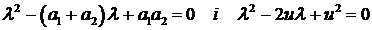
 аозначает, что в процессе стабилизации по
аозначает, что в процессе стабилизации по 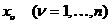
 амаховик лишь лпереводит малые возмущения в дополнительное вращение гиростата вокруг оси вращения
амаховик лишь лпереводит малые возмущения в дополнительное вращение гиростата вокруг оси вращения 
Покажем,
что при 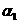 арешение этой задачи дает линейный закон правления
арешение этой задачи дает линейный закон правления
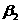 (3.2.4)
(3.2.4)
где 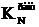

Для доказательства рассмотрим линейную подсистему, описываемую поведение 
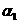 аэта подсистема полностью правляема. Поэтому коэффициенты в
аэта подсистема полностью правляема. Поэтому коэффициенты в 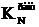 аможно выбрать так, что положение равновесия
аможно выбрать так, что положение равновесия 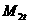 алинейной части системы
(3.2.3) равномерно стойчиво по Ляпунову. Поскольку нелинейные члены в системе
(3.2.3) обращаются в нуль при
алинейной части системы
(3.2.3) равномерно стойчиво по Ляпунову. Поскольку нелинейные члены в системе
(3.2.3) обращаются в нуль при 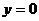
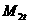 самой нелинейной системы (3.2.3).
самой нелинейной системы (3.2.3).

Рис.
3.2.2 График изменения переменной 

Рис.
3.2.3 График изменения переменной 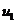 апри гашении возмущений
апри гашении возмущений
Техническая реализация закона правления (3.2.4) сводиться к следующему. Пока гиростат совершает заданное движение (3.2.2), маховик находится в состоянии покоя (управляющий двигатель включен). При появлении малых постоянных возмущений специальные стройства формируют и прикладывают к маховику правляющий момент (3.2.4). В результате основное тело гиростата с течением времени возвращается в исходный режим стационарного вращения, сам маховик - в состояние покоя.
Приведем результаты моделирования замкнутой системы (3.2.3), (3.2.4) при значениях параметров 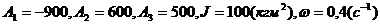 аи начальных данных
аи начальных данных 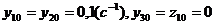
 аподчинено ограничению
аподчинено ограничению 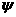
Расчет показывает, что коэффициенты 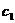 аможно выбрать в виде
аможно выбрать в виде 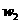
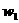
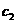
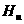
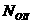
 а(графики
а(графики 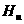 апримерно такие же, как по харатеру, так и по скорости сходимости) и правления
апримерно такие же, как по харатеру, так и по скорости сходимости) и правления 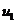
3.3 Динамическое уравнение Эйлера, описывающее гловое движение твердого тела под действием правляющих моментов
Рассмотрим динамические уравнения Эйлера
 (3.3.1)
(3.3.1)
описывающие вызванное начальными возмущениями гловое движение твердого тела относительно центра масс под действием ауправляющих моментов 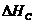
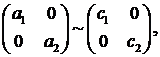
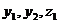
Предположим,
что 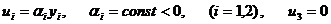
В качестве функции Ляпунова  авозьмем кинетическую энергию тела
авозьмем кинетическую энергию тела

Поскольку
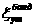
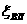
то положение равновесия тела стойчиво (неасимптотически)
по Ляпунову. Значит, для каждого 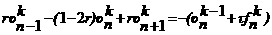 анайдутся числа
анайдутся числа 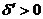 аи
аи 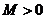 атакие, что
атакие, что
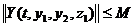
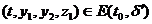
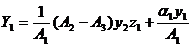
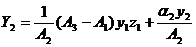
Поэтому при любых 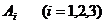 афункция
афункция  аудовлетворяет всем условиям теоремы 3.1.2.
аудовлетворяет всем условиям теоремы 3.1.2.
Следовательно,
положение равновесия тела асимптотически стойчиво по отношению к 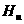
Можно отметить, что для функции  амножество
амножество 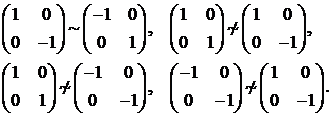 аявляется гиперплоскостью
аявляется гиперплоскостью 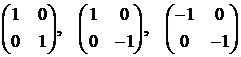
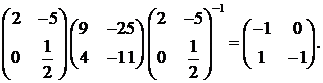
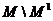 апусто и,
следовательно, не содержит целых траекторий системы (3.1.3). вместе с тем в множествах
апусто и,
следовательно, не содержит целых траекторий системы (3.1.3). вместе с тем в множествах 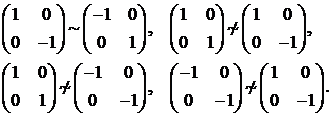 аи
аи 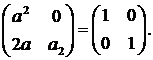 аесть целые траектории системы (3.1.3) вида
аесть целые траектории системы (3.1.3) вида 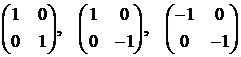
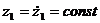
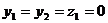
 аудовлетворяет всем условиям теоремы 3.1.4, но не довлетворяет всем словиям теорем 3.1.3, 3.1.5.
аудовлетворяет всем условиям теоремы 3.1.4, но не довлетворяет всем словиям теорем 3.1.3, 3.1.5.
В случае  а(или
а(или 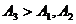
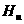 аположения равновесия тела может быть доказана с помощью функции
аположения равновесия тела может быть доказана с помощью функции
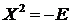
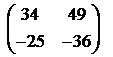
В этом случае выполняются словия теоремы 3.1.6
И значит,
в этом случае имеем асимптотическую стойчивость по 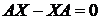 апри любом значении
апри любом значении 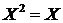
Это свойство сохраняется и при постоянно действующих возмущениях 
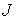 авида
авида 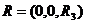
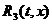 а в области
а в области 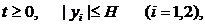 а
а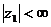 авыполняются словия существования, единственности и
авыполняются словия существования, единственности и 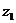
Таким образом, имеет место инвариантность свойства асимптотическойа стойчивости при постоянно действующих возмущениях казанного типа.
3.4 Динамическое уравнение Эйлера, описывающее гловое движение твердого тела под действием постоянно действующих возмущений
Рассмотрим систему (3.3.1),
замкнутую правлением 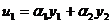
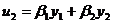
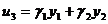
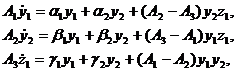 (3.4.1)
(3.4.1)
Если предположить, что на систему (3.4.1) действуют возмущения 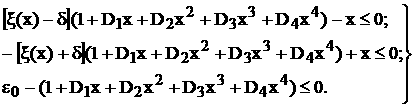
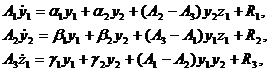 (3.4.2)
(3.4.2)
где 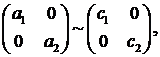
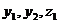
Вектор - функции 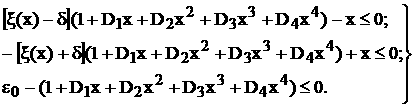 атакие, что система (3.3.1)
имеет решение, отвечающее каждому набору начальных данных
атакие, что система (3.3.1)
имеет решение, отвечающее каждому набору начальных данных 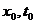 аи
аи 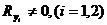
В случае  а(или
а(или 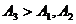
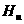 аположения равновесия тела может быть доказана с помощью функции
аположения равновесия тела может быть доказана с помощью функции
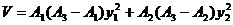
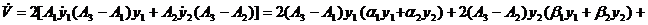
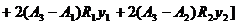
Выбор 
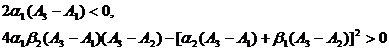
Это гарантирует выполнения требований теорем 2.3.1 и 3.1.7.
Значит система (3.4.2)
при постоянно действующих возмущениях будет 
Заключение
За последнее десятилетие развитие теории частичной стойчивости (стабилизации) было существенным. Более того, именно в этот период появились дополнительные стимулы к дальнейшей разработке такой теории. Помимо традиционных и не теряющих актуальности задач механики, частичная стойчивость оказалась подходящим понятием в бурно развивающихся на стыке физики и теории правления методах правления хаосом, частичное правление стало систематически исследоваться на стыке химии и теории управления. Получили развитие и ряд других теоретических и прикладных разделов современной нелинейной теории правления, посвященных различным аспектам инвариантности нетривиальных множеств и аттрактивности многомерных геометрических объектов, также тесно связанных с концепцией частичной стойчивости.
Направления исследования позволяют в значительной степени по-новому смотреть как на саму проблематику задач частичной устойчивости (стабилизации) и место этих задач в общей теории динамических систем, так и на перспективы их развития, ведь термины частичная устойчивость, частичная стабилизация, помимо технической сферы, используются при анализе химических процессов, в экономике и политике. Несмотря на появление и развитие новых более общих задач той же направленности, задачи частичной устойчивости (стабилизации) для систем обыкновенных дифференциальных уравнений с интересной и поучительной историей их развития будут оставаться важным звенома дальнейших исследований.
Для достижения поставленной цели исследования были решены следующие задачи:
1) проанализирована научная литература, посвящённая проблеме стойчивости и стабилизации движения при постоянно действующих возмущениях и применены эти исследования для решения практической задачи;
2) рассмотрена устойчивость и стабилизацию движений относительно частим переменных при постоянно действующих возмущениях для линейных систем;
3) раскрыты определения стойчивости и стабилизации движения относительно части переменных при постоянно действующих возмущениях;
4)
рассмотрены основные теоремы, исследующие словия  ;
;
5) рассмотрена устойчивость и стабилизацию движений относительно части переменных при постоянно действующих возмущениях для нелинейных систем;
6) с помощью метода функций Ляпунова рассмотрен ряд теорем об стойчивости движения относительно части переменных при постоянно действующих возмущениях;
7) рассмотрена оптимальная стабилизация нелинейных систем при наличии постоянно действующих возмущений;
8) проведен анализ стойчивости и стабилизации движений относительно части переменных для конкретной математической модели с использованием современных методов.
В процессе теоретического исследования в соответствии с его целью и задачами получены достаточные условия 

