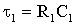1. Решить задачу об использовании сырья геометрическим способом и симплекс методом, дать экономическую интерпретацию.

75	5	3
83	4	7
50	1	5
	4	5

Геометрический способ.

Пусть аколичество выпускаемой продукции первого вида, тогда аколичество выпускаемой продукции второго вида. Прибыль от реализации всей продукции составляет

Цель задачи (максимализация прибыли) запишется в виде

Расход ресурса

Запас ресурса

Структура всех трёх ограничений одинаков

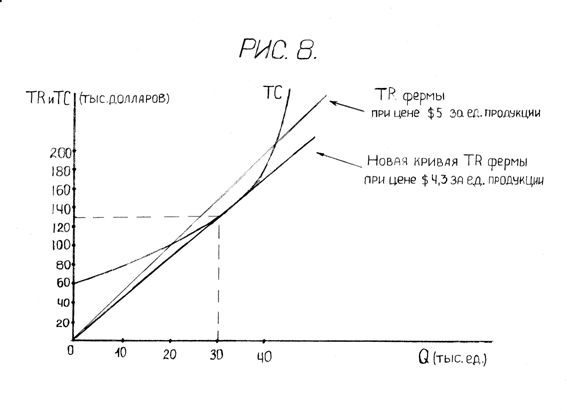
Перейдём из неравенств к уравнениям

Построим прямые на плоскости

Многоугольник решений апостроим начальную прямую аи вектор авдоль вектора аполучим, что максимальное значение наша прямая принимает в точке аточке пересечения прямых аи

Симплекс метод.

Приведём систему неравенств к системе равнений

Целевая функция - функция прибыли

Составим симплекс таблицу:

- Первое ограничение запишем в первую строку

- Второе ограничение запишем во вторую строку

- Третье ограничение запишем в третью строку

Целевую функцию запишем в астроку

Б	З
	75	5	3	1	0	0
	83	4	7	0	1	0
	50	1	5	0	0	1
	0			0	0	0

В строке аесть отрицательные аначальный план не оптимален. Найдём наименьший отрицательный элемент строки абудет включена в базис. Столбец переменной Ц ведущий. Подсчитаем симплексные отношения и найдём среди них минимальное атретья строка ведущая, а элемент аразрешающий. Следовательно переменная авыйдет из базиса.

Проведём одну интеракцию метода замещения Жордано-Гаусса. Столбцы. Разрешающий элемент

равен аподелим третью строку на 5, столбец асделаем единичным для этого третью строку множим на аи прибавим к первой строке, третью строку множим на аи сложим со второй строкой; третью строку сложим со строкой

Б	З
	45		0	1	0
	13		0	0	1
	10		1	0	0
	50		0	0	0	1

В строке аесть отрицательные аплан не оптимальный. Рассчитаем симплексные отношения и найдём среди них минимальное авторая строка ведущая аразрешающий

Следовательно, переменная авыйдёт из базиса. Так как разрешающий элемент ана аотличны от элемента асделаем нулевыми, для этого вторую строку множим на аи прибавим к первой; вторую строку множим на аи прибавим к третьей; вторую строку множим на аи прибавим к строке

Б	З
	23	0	0	1
	5	1	0	0
	9	0	1	0
	65	0	0	0

В строке аесть отрицательный элемент - пересчитываем таблицу. Рассчитываем симплексные отношения и найдём среди них минимальные апервая строка ведущая аразрешающий элемент апеременная авыйдет из базиса. Сделаем элемент аединичным, для этого поделим первую строку на асделаем единичным для этого первую строку множим на аи прибавим ко второй строке. Первую строку множим на аи прибавим к третьей. Первую строку множим на аи прибавим к строке

Б	З
	13	0	0			1
	12	1	0			0
	5	0	1			0
	73	0	0			0

Так как в строке авсе элементы неотрицательны, то найден оптимальный план

Оптимальный план найденный геометрическим способом и симплексным методом совпадают. Предприятию необходимо выпускать 12 единиц продукции первого вида и 5 единиц продукции второго вида. В этом случае предприятие получит прибыль аденежных единиц.

2. Решить транспортную задачу распределительным методом, оценивая свободные клетки по методу потенциалов.

	60	50	85	75
65	8	10	6	5 65
80	4 30	3 50	5	9
35	11 25	4	4	8 10
90	5 5	5	3 85	6

Проверим необходимое и достаточное словие разрешимости задачи

Потребность в грузе равна запасам груза азадача закрытая, следовательно, имеет единственное решение.

Используя метод наименьшей стоимости заполним таблицу.

Среди тарифов наилучшим является аи

в клетку а

в клетку

в клетку

в клетку

в клетку

в клетку

в клетку

Запасы поставщиков исчерпаны, запросы потребителей довлетворены полностью. В результате получили первый опорный план. Подсчитаем число занятых клеток таблицы их 7, должно быть аопорный план не вырожденный.

Определим значение целевой функции первого опорного плана

Проверим оптимальность плана.

Найдём потенциалы аи апо занятым клеткам таблицы

Пусть

Подсчитаем оценки свободных клеток

Первый опорный план не является оптимальным так как

Переходим к его лучшению. Для клетки астроим цикл перераспределения

В результате получили новый опорный план

	60	50	85	75
65	8	10	6	5 65
80	4 55	3 25	5	9
35	11	4 25	4	8 10
90	5 5	5	3 85	6

Определим значение целевой функции

Проверим оптимальность плана

Подсчитаем оценки свободных клеток

План близок к оптимальному.

При дальнейшем перераспределении груза, задача входит в циклическую фазу, план не лучшается. Таким образом, полученное решение является наиболее оптимальным для нашей задачи