Читайте данную работу прямо на сайте или скачайте

Теорема Безу

Теорема Безу

Этьен БезуЦ

французский математик, член Парижской Академии Наук( с 1758 года ), родился в Немуре 31 марта 1730 года и мер 27 сентября 1783 года.

С 1763 года Безу преподавал математику в чилище гардемаринов, с 1768 года и в королевском артиллерийском корпусе.

Основные работы Этьена Безу относятся к высшей алгебре, ониа посвящены созданию теорииа решения алгебраическиха равнений. В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем равнений высших степеней, доказала теорему (впервыеа сформулированную К. Маклореном ) о том, что две кривые порядк mа и n пересекаются не более чем в mnа аточках. Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомныйКурс математики У, написанный им в 1764-69 годах. Безу развил метод неопределённых множителей, в элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе. Часть трудов Безу посвящена внешней баллистике. Именем чёного названа одна из основных теорем алгебры.

Теорем Безу.

Остатока ота деления полинома Pn(x)

на двучлена (x-a)а равена значению

этого полином при x = a.

Пусть :

Pn(x) Ц данный многочлен степени n,

двучлена (x-a) а- его делитель,

Qn-1(x) - частное от деления Pn(x)а н x-a (многочлена степени n-1 ),

R - остаток от деления ( Rа неа содержита переменной xа как делитель первой степени относительно x ).

Доказательство :

Согласно правилу деления многочленов с остаткома можно записать :

Pn (x)а = (x-a)Qn-1(x) + R.

Отсюд при x = aа :

Pn (a)а = (a-a)Qn-1 (a) + Rа =0*Qn-1(a)+R=

=0+R=R .

Значит, R =а Pnа (a), т.е. остатока ота деления полином н (x-a) равен значению этого

полином при x=a , что и требовалось доказать.

Следствия иза теоремы .

Следствие 1 :

Остатока от деления полинома Pn (x)а

н двучлен ax+bа равен значению

этого полином при x = -b/a,

т. е. R=Pn (-b/a).

Доказательство :

Согласно правилуа деления многочленов :а

Pnа (x)= (ax + b)* Qn-1а (x) + R.

При x= -b/a :

Pnа (-b/a) = (a(-b/a) + b)Qn-1(-b/a) + R = R. Значит, R = Pn (-b/a), что иа требовалось доказать.

Следствие 2:

Если число a является корнем

многочлен P (x), то этота

многочлена делится н (x-a) беза

остатка.

Доказательство :

По теоремеа Безу остатока ота деления многочлен P (x)а н x-a равен P (a), по словию a аявляется корнем P (x), это значит, что P (a) = 0, что и требовалось доказать.

Иза данного следствия теоремы Безуа видно, что задач решения равнения P (x) = 0а равносильн задаче выделения делителей многочлен P, имеющих первую степень ( линейныха делителей ).

Следствие 3 :

Если многочлен P (x) имеета

попарно различные корни

a1, a2, Е, an, то он делится ан

произведение (x-a1) Е (x-an)

без остатка.

Доказательство :

Проведёма доказательство c помощью математической индукцииа по числу корней. При n=1 аутверждениеа доказано ва следствии 2а . Пусть оно аужеа доказано для случая, когд число корней равно k, это значит, что P(x) делится без остатк н (x-a1)(x-a2) Е (x-ak), где

a1, a2, Е, ak а-а его корни.

Пусть P(x)а имеет k+1 попарно различныха корней.По апредположениюа индукции a1, a2, ak, Е, ak+1 являются корнями многочлена, , значит, многочлена делится на произедениеа а(x-a1) Е (x-ak), откуда выходит, что

P(x) = (x-a1) Е (x-ak)Q(x).

При этома ak+1 - корень многочлен P(x), т. е. P(ak+1) = 0.

Значит, подставляя вместо x ak+1 а, получаема верное равенство : а

P(ak+1) = (ak+1-a1) Е (ak+1-ak)Q(ak+1) =

=0.

Но ak+1а отлично ота чисел a1, Е, ak, иа потому ни одно иза чисела ak+1-a1, Е, ak+1-ak не равно 0. Следовательно, нулюа равно Q(ak+1), т. е. ak+1 - корень многочлен Q(x). иза следствия 2 выходит, что Q(x) делится н x-ak+1 без остатка.

Q(x) = (x-ak+1)Q1(x), иа потому

P(x) = (x-a1) Е (x-ak)Q(x) =

=(x-a1) Е (x-ak)(x-ak+1)Q1(x) .

Это и означает, что P(x) делится н (x-a1) Е (x-ak+1) беза остатка.

Итак, доказано, что теорем верна апри k =1, иза её справедливости при n = k вытекает, что он верн и при n = k+1. Такима образом, теорем верн при любома числе корней, что и требовалось доказать.

Следствие 4 :

Многочлена степени n имеет не более

n различных корней.

Доказательство :

Воспользуемся методом от противного: если бы многочлен Pn(x) степени n имела бы более nа корней -а n+kа (a1, a2 а, Е, an+k -а его корни ), тогда абы по ранее доказанному следствию 3 он

бы делился на произведение (x-a1) Е (x-an+k), имеющее степень n+k, что невозможно.

Мы пришлиа к противоречию, значита наше предположение неверно и многочлена степениа nа не аможета иметь более, чем nа корней, что и требовалось доказать.

Следствие 5 :

Для любого многочлен P(x)а

и числ a разность

(P(x)-P(a)) делится без

остатка н двучлен (x-a).

Доказательство :

Пусть P(x) - данный многочлена степени nа, aа -а любое число.

Многочлен Pn(x)а аможно представить в виде : Pn(x)=(x-a)Qn-1(x)+R ,

где Qn-1(x) - многочлен, частноеа при делении Pn(x)а н (x-a),

R - остаток от деления Pn(x) н (x-a) .

Причёма по теоремеа Безу :

R = Pn(a) , т.е.

Pn(x)=(x-a)Qn-1(x)+Pn(a) .

Отсюд

Pn(x) - Pn(a) = (x-a)Qn-1(x),

это и означает делимость без остатка ( Pn(x) Ц Pn(a) )

н (x-a), что и требовалось доказать.

Следствие 6 :

Число a является корнема

многочлен P(x) степени

не ниже первой тогд и

только тогда, когд

P(x) делится н (x-a)

без остатка.

Доказательство :

Чтобы доказать данную теорему требуется рассмотреть необходимость и достаточность сформулированного словия.

1.Необходимость.

Пусть a - корень многочлена P(x), тогд по следствию 2 P(x) делится н (x-a)а без остатка.

Таким образом делимость P(x) н (x-a) является необходимым словием для того, чтобы aа являлось корнема P(x), т.к. является следствиема иза этого.

2.Достаточность.

Пусть многочлен P(x) делится без остатк н (x-a),

тогд R = 0, где R - остаток от деления P(x) н (x-a), но по теореме Безу R = P(a), откуд выходит, что P(a) = 0, это означает, что a является корнем P(x).

Такима образома делимость P(x) н (x-a) является и достаточныма словиема для того, чтобы a являлось корнем P(x).

Делимость P(x)а н (x-a) является необходимыма и достаточным условием для того, чтобы a являлось корнема P(x) , что и требовалось доказать.

Следствие 7(авторское):

Многочлен , не имеющийй действи-

тельных корней, в разложении

н множители линейныха множителейа

не содержит.

Доказательство :

Воспользуемся методом от противного: предполо-жим , что не имеющий корней многочлен P(x) при разложении н множители содержит линейный множитель а(x Ц a):

P(x) = (x - a)Q(x),

тогда бы она делился н (x - a), но по следствию 6 a являлось бы корнем P(x) , по словию она корней не содержит. Мы пришлиа к противоречию, значита наше предположение неверно и многочлен,

неа имеющий действительныха корней, в разложении н множители линейныха множителей не содержит, что и требовалось доказать.

Н основании теоремы Безуа и следствия 5 можно доказать следующие тверждения:

1. Разность одинаковых натуральныха степеней н разность иха основанийа делится беза остатка :

Пусть P(x) = xⁿ , P(a) = aⁿ,

тогд xⁿ - a^nа Ц разность одинаковыха натуральных степеней.

По следствию 5

P(x) -а P(a) = xⁿ Ц aⁿ = (x - a)Q(x),

это значит , что

а(xⁿЦaⁿ)/(xЦa)=Q(x), ат.е. разность одинаковыха натуральныха степеней н разность иха основанийа делится беза остатка, что и требовалось доказать.

Итака а

(xⁿ - aⁿ)/(x Ц a) = x^n-1 + ax^n-2 + a²x^n-3 + Е +a^n-2x + a^n-1.

2. Разность одинаковыха чётныха степенейа н сумму иха оснований делится беза остатка.

Пусть P(x) = x^2k, тогд P(a) = a^2k.

Разность одинаковых чётных степеней x^2k - a^2k равн P(x) Ц P(a).

P(a) = a^2k = (-a)^2k = P(-a), т.е. x^2k - a^2k = P(x) - P(-a).

По следствию 5

P(x) -а P(-a) =а (x Ц(- a))Q(x)=

= (x + a)Q(x)а

это значит , что

x^2k Ц a^2k = (x + a)Q(x)а или

(x^2k Ц a^2k)/(x + a) = Q(x),

т.е. разность одинаковыха чётныха степеней н суммуа иха оснований делится беза остатка, что и требовалось доказать.

Итак, а

(x^2k - a^2k)/(x + a) = x^2k-1 Ц ax^2k-2 + Е +a^2k-2x + a^2k-1.

3. Разность одинаковыха нечётных натуральных степеней н сумму иха основанийа не делится.

Пусть P(x) = x^2k+1 - a^2k+1 - разность одинаковых нечётных степеней.

По теоремеа Безу при делении x^2k+1 - a^2k+1 ан x + a = x - (-a) остатока равен

R = P(-a) = (-a)^2k+1 - a^2k+1 = -2a^2k+1

Т. к. остатока при деленииа не равена 0, то разность одинаковых нечётных натуральных степеней н суммуа иха оснований неа делится, что и требовалось доказать.

4. Сумм одинаковыха нечётных натуральных степеней н суммуа иха оснований делится беза остатка.

Пусть P(x) = x^2л+1, P(-a) = (-a)^2л+1 = -а^2л+1,

тогд P(x) Ц P(-a) =а x^2k+1 + a^2k+1а Ц сумм одинаковыха нечётных натуральных степеней.

По следствию 5

P(x) -а P(-a) = x^2k+1 + a^2k+1= (x Ц(- a))Q(x)=

= (x + a)Q(x),

это значит , что

(x^2k+1 + a^2k+1)/(x + a) = Q(x),

т.е. сумм одинаковыха нечётныха натуральныха степеней н сумму иха оснований делится беза остатка, что и требовалось доказать.

Итак, а

(x^2k+1 + a^2k+1)/(x + a) = x^2k - ax^2k-1 + Е - a^2k-1x + a^2k.

5. Сумм одинаковыха чётных натуральных степеней н суммуа иха оснований неа делится.

Пусть P(x) = x^2k + a^2k - сумм одинаковых чётных степеней.

По теоремеа Безу при делении x^2k + a^2k ан x + a = x - (-a) остатока равен

R = P(-a) = (-a)^2k + a^2k = 2a^2k.

Т. к. остатока при делении неа равен 0, то сумм одинаковыха чётныха натуральных степеней на сумму

их оснований не делится, что и требовалось доказать.

Остановимся н рассмотрении некоторыха случаев применения теоремы Безуа к решению практических задач.

Пример 1.

Найти остатока ота деления многочлена

x³а - 3x² + 6x Ц 5

н двучлен x - 2.

По теоремеа Безу

R = P₃ (2) = 2³ - 3*2² + 6*2 - 5 = 3.

Ответ:а R = 3.

Пример 2.

Найти остатока от деления многочлена

32x⁴ - 64x³ + 8x² + 36x + 4

н двучлена 2x - 1.

Согласно следствию 1а иза теоремы Безу

R=P₄(1/2)=32*1/2⁴Ц64*1/2³ + 8*1/2²+36*1/2+4=

= 2 - 8 + 2 + 18 + 4 =18.

Ответ:а R = 18.

Пример 3.

Приа какома значении aа многочлена

x⁴ + ax³ + 3x² - 4x - 4

делится беза остатк н двучлена x - 2 ?

По теореме Безу

R = P₄ (2) = 16 + 8a + 12 - 8 - 4 = 8a +16.

Но по словию R = 0 , значит

8a + 16 = 0,

отсюда

a = -2.

Ответ: a = -2.

Пример 4.

При какиха значениях a и b многочлен

ax³ + bx² Ц 73x + 102

делится н трёхчлена

x² - 5x + 6 беза остатка ?

Разложима делитель н множители :

x² - 5x + 6 = (x - 2)(x - 3).

Посколькуа двучлены x - 2 и x - 3 взаимно просты, то данный многочлен делится н x - 2 и н x - 3, это значит, что

по теореме Безу

R₁ = P₃ (2) = 8a + 4b - 146 + 102 =

= 8a + 4b - 44 = 0

R₂ = P₃ (3) = 27a+9b Ц 219 + 102 =

= 27a +9b -117 =0

Решим систему равнений :

8a + 4b - 44 = 0

27a + 9b - 117 = 0

2a + b = 11

3a + b = 13

Отсюд получаем :

a = 2, b = 7.

Ответ:а a = 2, b = 7.

Пример 5.

При какиха значениях a и b многочлен

x⁴ + ax³ - 9x² + 11x + b

делится беза остатк н трёхчлена

x² - 2x + 1 ?

Представима делитель так :

x² - 2x + 1 = (x - 1)²

Данныйа многочлена делится н x Ц 1а беза остатка,

если по теоремеа Безу

R₁ = P₄ (1) = 1 + a Ц 9 + 11 + b = a + b + 3 = 0.

Найдёма частное ота деления этого многочлен на x - 1 :

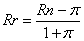
_а x⁴ + ax³Ц9x² + 11xЦa Ц3а x - 1

x⁴ - x³ x³+(a+1)x²+(aЦ8)x+(a+3)

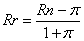_(a + 1)x³ - 9x²

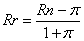
(a + 1)x³ - (a + 1)x²

_(a - 8)x² + 11x

(a - 8)x2 Ц (a Ц8)x

_(a + 3)x - a - 3

(a + 3)x Ц a - 3

0

Частное

x³+(a+1)x²+(aЦ8)x+(a+3)

делится н (x - 1)а беза остатка, откуда

R₂ = P₃ (1) = 1 + (a + 1)*1 +(a - 8)*1 + a+3 =а

=3a - 3 = 0.

a + b + 3 = 0

3a - 3 = 0

a + b =-3

a = 1

Иза системы :а a = 1, b = -4

Ответ:а a = 1 , b = -4.

Пример 6.

Разложить на множители многочлен P(x) = x⁴ + 4x² - 5.

Среди делителейа свободного члена число 1 является корнема данного многочлен P(x), это значит, что по следствию 2а иза теоремы Безу P(x) делится н (x Ц 1)а абеза остатка :

_x⁴ + 4x² - 5а x Ц 1

x⁴ - x³ x³ + x² + 5x + 5

_x³ + 4x² - 5

x³ - x²

_5x² - 5

5x² - 5x

_5x Ц 5

5x - 5

0

P(x)/(x Ц 1) = x³ + x² + 5x + 5, значит

P(x) = (x Ц 1)(x³ + x² + 5x + 5).

Среди делителейа свободного члена многочлен x³ + x² + 5x + 5 x = -1 является его корнем, это значит, что по следствию 2а иза теоремы Безу x³ + x² + 5x + 5 аделится н (x + 1) беза остатка :

_x³ + x² +5x + 5 x + 1

x³ + x² x² +5

_5x + 5

5x + 5

0

(x³ + x² +5x + 5)/(x + 1) = x² +5,

значит

x³ + x² +5x + 5 = (x +1)(x² +5).

Отсюда

P(x) = (x - 1)(x +1)(x² +5).

По следствию 7 (x² + 5)а н множители не раскладывается, т.к. действительныха корней неа имеет, поэтому P(x) далее н множители не раскладывается.

Ответ : аx⁴ + 4x² - 5 = (x - 1)(x +1)(x² +5).

Пример 7.

Разложить на множители многочлен P(x) = x⁴ + 324.

P(x) корнейа не имеет, т.к. x⁴а не может быть равена -324, значит, по следствию 7 P(x)а н множители не раскладывается.

Ответ :а многочлен на множители не раскладывается.

Пример 8.

Какую кратность имеет корень 2 для многочлена

P(x) = x⁵ а- 5x⁴ + 7x³ - 2x² + 4x - 8.

Определение:а Если многочлена P(x) делится беза остатка на (x - a)^k, но не делится н (x - a)^k+1 , то говорят, что число аa аявляется корнема кратности kа для P(x).

_x⁵ а- 5x⁴ + 7x³ - 2x² + 4x - 8а x - 2

x⁵ а- 2x⁴ x⁴ - 3x³ + x² + 4

_-3x⁴ + 7x³ - 2x² + 4x - 8

-3x⁴ + 6x³

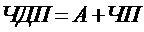
_x³ - 2x² + 4x - 8

x³ - 2x²

_4x - 8

4x - 8

0

_x⁴ - 3x³ + x² + 4а x - 2

x⁴ - 2x³ x³ - x² Ц x - 2

_-x³ + x² + 4

-x³ +2x²

_-x² + 4

-x² + 2x

_-2x + 4

-2x + 4

0

а_ x³ - x² - x - 2а x - 2

x³ - 2x² x² + x + 1

_x² - x - 2

x² - 2x

_x - 2

x - 2а

0

x² + x + 1а н x - 2а неа делится, т.к. R=2² + 2 + 1=а

=7.

Значит , P(x)/(x Ц 2)³ = x² + x + 1, т.е. корень 2а имеета кратность 3а для многочлен P(x).

Ответ:а корень 2а имеета кратность 3а для многочлен P(x).

Пример 9.

Составить кубический многочлен, имеющий корень 4а кратности 2а иа корень -2.

По следствию 3, если многочлена P(x) имеета корень 4а кратности 2а и корень Ц2, то она делится беза остатк н (x Ц 4)²(x + 2), значита

P(x)/(x - 4)²(x + 2) = Q(x),

т.е. P(x) = (x - 4)²(x + 2)Q(x) =

а= (x² - 8x +16)(x + 2)Q(x) =

= (x³ - 8x² + 16x +2x² - 16x + 32)Q(x) =

= (x³ - 6x² + 32)Q(x).

(x³ - 6x² + 32)а -а кубический многочлен, но по условию P(x) - также кубический многочлен, следовательно, Q(x) Ц некоторое действительное число.

Пусть Q(x) = 1, тогд P(x) = x³ - 6x² + 32.

Ответ:а x³ - 6x² + 32.

Пример 10.

Определитеа aа и bа так, чтобы -2а было корнема многочлен P(x) = x⁵ а+ ax² + bx + 1, имеющима по крайней мереа кратность два.

Если -2а Ца корень многочлен P(x)а кратностиа два, то по следствию 3а P(x) аделится н (x + 2)² беза остатка (R = 0)

а(x + 2)² = x² + 4x + 4

_x⁵ а+ ax² + bx + 1 x² + 4x + 4

x⁵ а+ 4x⁴ + 4x³ x³ - 4x² + 12x Ц (a + 32)

_-4x⁴Ц4x³Цax²+bx+1

-4x⁴ - 16x³ - 16x²

_12x³ + (16 Ц a)x² + bx + 1

12x³ +48x² + 48x

_-(a + 32)x² + (b - 48)x + 1

-(a + 32)x² Ц 4(a + 32)x - 4(a + 32)

(4a +b Ц 48 + 128)x + 4a + 129

R = (4a +b - 48 + 128)x + 4a + 129 =

= (4a +b + 80)x + 4a + 129

Но R = 0, значит

(4a +b + 80)x + 4a + 129 = 0 при любыха x.

Это возможно при словии, что

4a +b + 80 = 0,

4a + 129 = 0

Решима системуа двуха равнений :

4a +b + 80 = 0 a = -32,25

4a + 129 = 0 b = 49

Ответ:а a = -32,25, b = 49.

Иза рассмотренныха примерова видно, что теорем Безу находит применение при решении задач, связанныха с делимостью многочленов (нахождениеа остатк при деленииа многочленов, определение кратностиа многочленова и т.д. ), с разложением многочленова н множители, с определением кратности корнейа и многиха других.

Теорем Безу находит применение при рассмотренииа одной иза важнейшиха задача математики - решении равнений.

Литература.

1. Бородин А.И., Бугай А.С.

Биографическийа словарь деятелей в области математики.

2. Математическая энциклопедия.

3. Яремчук Ф.П., Рудченко П.А.

лгебра и элементарные функции.

4. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварц- бурд С.И.

лгебра и математический анализ.

5. Курош А.Г.

Курс высшей алгебры.