Читайте данную работу прямо на сайте или скачайте

Решение задачи линейного программирования

(1)

Теорема. Если множество апланов задачи (1) не пусто и целевая функция асверху ограничена на этом множестве, то задача (1) имеет решение.

Теорема. Если множество адопустимых планов имеет крайние точки и задача (1) имеет решение, то среди крайних точек найдется оптимальная.

Метод исключения Жордана-Гаусса для системы линейных уравнений.

Большинство из существующих численных методов решения задач линейного программирования использует идею приведения системы линейных равнений

которая в матричной форме записывается в виде

В первом равнении системы отыскивается коэффициент ава остальных равнениях системы. Для этого первое равнение множается на число аи прибавляется к уравнению с номером априсутствует только в первом равнении, и притом с коэффициентом 1. Переменная аназывается базисной переменной.

налогичная операция совершается поочередно с каждым равнением системы; при этом всякий раз преобразуются все равнения и выполняется список базисных переменных.

Результатом применения метода Жордада-Гаусса является следующее: либо станавливается, что система несовместна, либо выявляются и отбрасываются все лишние равнения; при этом итоговая система равнений имеет вид

где Ч список номеров базисных переменных, Ч множество номеров небазисных переменных. Здесь Ч ранг матрицы акоэффициентов исходной системы равнений.

Полученную системы равнений называют приведенной системой, соответствующей множеству аномеров базисных переменных.

Симплекс-метод.

Симплекс Цметод, метод последовательного лучшения плана, является в настоящее время основным методом решения задач ЛП.

Рассмотрим каноническую задачу ЛП

где векторы аи аи будем предполагать, что все гловые точки аявляются невырожденными.

, где вектор аопределяется формулой

Теорема. Если в гловой точке авыполняется словие Ч решение задачи (2).

Теорема. Для того, чтобы гловая точка аявлялась решением задачи (2), необходимо и достаточно, чтобы в ней выполнялось словие

лгоритм симплекс-метода.

Переход из старой гловой точки ав новую гловую точку асостоит, в сущности, лишь в изменении базисной матрицы авводится вектор

Шаг 0. Задать целевой вектор аи множество базисных индексов аи вектор

Шаг 1. Вычислить матрицу аи вектор

Шаг 2. Вычислить вектор потенциалов аи оценки

Шаг 3. Если адля всех Ч базисный вектор оптимального плана; иначе перейти на шаг 4.

Шаг 4. Выбрать произвольный индекс аи вычислить вектор

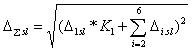
Шаг 5. Если

Шаг 6. Сформировать множество индексов аи вычислить

Шаг 7. В множестве аиндекс азаменить на индекс Ч вектор Ч на вектор Ч компоненту ана