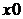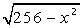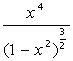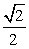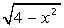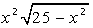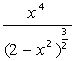Читайте данную работу прямо на сайте или скачайте
Решение инженерных задач на ЭВМ
Введение.4
1. Глава 1. Погрешности..4
з 1 Общая схема вычислительного эксперимента...4
з 2. Абсолютная и относительная погрешность..5
з 3. Основные источники погрешностей..6
з 4. Десятичная запись приближенных чисел. Значащая цифра. Число верных знаков..7
з 5. Связь относительной погрешности приближенного числа с количеством верных знаков этого числа..8
з 6. Погрешность суммы.9
з 7. Погрешность разности..9
з 8. Погрешность произведения.10
з 9. Число верных знаков произведения11
з 10. Погрешность частного11
з 11. Число верных знаков частного..11
з 12. Относительная погрешность степени...12
з 13. Относительная погрешность корня...12
з 14. Общая формула для погрешности.12
з 15.Обратная задача теории погрешностей.13
Лабораторная работа № 1 Вычисление сопротивлений в электрических цепях..14
Лабораторная работа № 2 Определение абсолютной и относительный погрешности.17
Лабораторная работа № 3 Действия над приближенными значениями чис..18
Вопросы для самопроверки19
Глава 2. Приближенное решение алгебраических и трансцендентных равнений.20
з 1. Сравнение линейных и нелинейных равнений20
з 2. Отделение корней.20
з3. Графическое решение равнений20
Лабораторная работа № 4. Расчет цепи содержащей диод, графическим способом21
Лабораторная работа № 5. Расчет и анализ неразветвленной электрической цепи переменного тока..23
з 4. Метод половинного деления25
Лабораторная работа № 6. Расчет цепи содержащей диод, методом дихотомии.25
з 5. Метод хорд26
Лабораторная работа № 7. Расчет цепи содержащей диод, методом хорд28
з 6. Метод Ньютона (метод касательных).28
Лабораторная работа № 8. Расчет цепи содержащей диод, методом Ньютона.29
з 7. Метод итерации30
Лабораторная работа № 9. Расчет цепи содержащей диод, методом итерации31
Вопросы для самопроверки33
Глава 3. Алгебра матриц.34
з1. Основные определения34
з2. Действия с матрицами.35
з3. Транспонированная матрица..37
з4. Обратная матрица38
з5 Степени матрицы..40
з6. Рациональные функции матрицы41
з7. Абсолютная величина и норма матрица.42
з8. Треугольные матрицы..43
з 9. Элементарные преобразования матриц.44
з10. Вычисление определителей44
Лабораторная работа № 10. Работа с матрицами.45
Лабораторная работа № 11. Обращение с помощью треугольных матриц48
Лабораторная работа № 12. Метод контурных токов..48
Глава 4. Система линейных алгебраических равнений..51
з 1. Определения, обозначения, основные сведения51
з2. Решение систем линейных уравнений по способу Гаусса.51
Лабораторная работа № 13. Расчет цепи постоянного тока, методом Гаусса...53
з3. Решение систем линейных уравнений по методу Зейделя59
Лабораторная работа № 14. Расчет цепи постоянного тока, методом Зейделя.61
з4. Решение систем линейных уравнений методом итераций64
Лабораторная работа № 15. Расчет цепи постоянного тока, методом итерации..66
з5. Применение метода Гаусса для вычисления определителей70
з6. Вычисление обратной матрицы методом Гаусса70
з7. Метод квадратных корней71
Задание 2. Метод зловых потенциалов. Заземлим точку D, при этом потенциал φd=0

Запишем фундаментальную систему уравнений (*)
φa*g11+φb*g12+φc*g13=J11
φa*g21+φb*g22+φc*g23=J22
φa*g31+φb*g32+φc*g33=J33
J11 = Ja = J-E1*g4 J22 = Jb = E2*g5-J J33 = Jc =0
Проводимости: g2 = 0
g11 = g2+g1+g4 = g1+g4 g22 = g2+g5+g3 = g5+g3 g33 = g1+g6+g3
g12= g21 =0 g13= g31 = -g1 g23= g32 = -g3
Согласно закону Ома имеем:
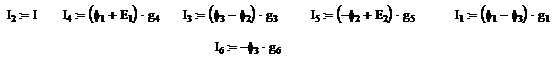
Проводимости

Решая систему

Еполучим

Соответственно токи имеют следующие величины (Ампер)

Потенциальная диаграмма

φn = 0
φa = φn-I2*r2 = -64 B φc = φa Ц I1*r1 = -76.688 Bа φd = φc+I6*r6 = -72.336 B
φm = φd-I5*r5 = -78 Bа φb = φm+E2 = -93.008 B
φn =UJ-φb = -0,028

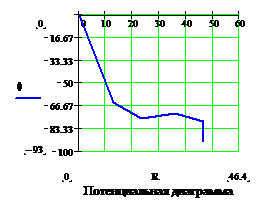
Ответ: I1=1.224 I2=5 I3=1.567 I4=3.776 I5=3.432 I6=0.344 (A)
Задание 3. Метод эквивалентного генератора. берем сопротивление r1. Найдем ток I1

По II закону Кирхгофа


Для определения I66 воспользуемся методом контурных токов
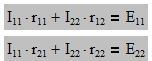
Поскольку в 3-ем контуре находится источник тока - исключим 1-ое равнение. Решая второе получим

Ответ: I1=1.224 (A)
з3. Решение системы линейных равнений по методу Зейделя
Для того чтобы применить метод Зейделя к решению системы линейных алгебраических равнений
Ax = b
с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду
x = Bx + c.
Здесь B - квадратная матрица с элементами bij (i, j = 1, 2, Е, n), c - вектор-столбец с элементами cij (i = 1, 2,.. n)
В развернутой форме записи система имеет следующий вид:
x1 = b11x1 + b12x2 + b13x3 + Е + b1nxn + c1
x2 = b21x1 + b22x2 + b23x3 + Е + b2nxn + c2
. ... ... ... ... ....
xn = bn1x1 + bn2x2 + bn3x3 + Е + bnnxn + cn
Вообще говоря, операция приведения системы к виду, добному для итераций, не является простой и требует специальных знаний, также существенного использования специфики системы.
Самый простой способ приведения системы к виду, добному для итераций, состоит в следующем. Из первого уравнения системы выразим неизвестное x1:
x1 = a11Ц1 (b1 Ц a12x2 - a13x3 - Е - a1nxn),
из второго равнения - неизвестное x2:
x2 = a21Ц1 (b2 Ц a22x2 - a23x3 - Е - a2nxn),
и т. д. В результате получим систему
x1 = b12x2 + b13x3 + Е +а b1,nЦ1xnЦ1 +а b1nxn+а c1
x2 = b21x1 + b23x3 + Е +а b2,nЦ1xnЦ1 +а b2nxn+а c2,
x3 = b31x1 + b32x2 + Е +а b3,nЦ1xnЦ1 +а b3nxn+а c3,
. ... ... ... ... ... ... ....
xn = bn1x1 + bn2x2 + bn3x3 + Е +а bn,nЦ1xnЦ1 + cn
в которой на главной диагонали матрицы B находятся нулевые элементы. Остальные элементы выражаются по формулам
bij = Цaij / aii, ci = bi / aii (i, j = 1, 2, Е, n, j ≠ i)
Конечно, для возможности выполнения указанного преобразования необходимо, чтобы диагональные элементы матрицы A были ненулевыми.
3.1. Описание метода.
Введем нижнюю и верхнюю треугольные матрицы
0 0 0 Е 0 0 b12 b13 b1n
b21 0 0 Е 0 0 0 b23а b2n
B1 =а b31 b32 0 0 , B2 = 0 0 0 Е b3n
.. ... ... ... .
bn1 bn2 bn3 0 0 0 0 Е 0
B = B1 + B2 и поэтому решение x исходной системы довлетворяет равенству x = B1x + B2x + c.
Выберем начальное приближение x(0) = [x1(0), x2(0), Е, xn(0)]. Подставляя его в правую часть равенства при верхней треугольной матрице B2 и вычисляя полученное выражение, находим первое приближение
x(1) = B1x(0) + B2x(1)
Подставляя приближение x(1), получим
x(2) = B1x(1) + B2x(2)
Продолжая этот процесс далее, получим последовательность x(0), x(1), Е, x(n), Е приближений к вычисляемых по формуле
x(k+1) = B1(k+1) + B2(k) + c
или в развернутой форме записи
x1(k+1) = b12x2(k) + b13x2(k) + Е +а b1nxn(k) + c1,
x2(k+1) = b21x1(k+1) + b23x3(k) + Е +а b2nxn(k) + c2,
x3(k+1) = b31x1(k+1) + b32x2(k+1) + +а b3nxn(k) + c3,
... ... ... ... ... ... ... ... ..
xn(k+1) = bn1x1(k+1) + bn2x2(k+1) + bn3x3(k+1) + Е + + cn.
Объединив приведение системы к виду, удобному для итераций и метод Зейделя в одну формулу, получим
xi(k+1) = xi(k) - aiiЦ1(∑j=1iЦ1 aijxj(k+1) + ∑j=1n aijxi(k) - bi).
Тогда достаточным словием сходимости метода Зейделя будет
∑j=1, j≠i n | aнij | < | aнii | (условие доминирования диагонали).
3.2. Метод Зейделя в матричной форме
Запишем систему в матричной форме:
*Х=Ва (1)
где А - матрица коэффициентов при неизвестных исходной системы, В - вектор-столбец свободных членов, X - вектор-столбец неизвестных. Обозначим, как принято в алгебре, через АТ результат транспонирования матрицы А. множим левую и правую части системы (2.22) слева на матрицу АТ:
Т *AX = АТ*B
Обозначим произведение АТ *Aа через С и АТ*B ачерез D. Преобразованная система теперь имеет вид:а C*X = D. (2)
Такого рода систему принято называть нормальной. Нормальные системы обладают рядом хороших свойств, среди которых, в частности, такие:
- матрица С коэффициентов при неизвестных нормальной системы является симметрической
(т. е. aij= aji, i,j = 1, 2,..., n)
- все элементы главной диагонали матрицы С нормальной системы положительны
(т. е. aij >0, i=1, 2, ...n).
Последний факт дает возможность лавтоматически приводить нормальную систему (1) к виду:
 а (i = 1, 2,....
n) (3)
а (i = 1, 2,....
n) (3)
где
 и
и  (4)
(4)
Целесообразность осуществления описанных преобразований вытекает из того, что имеет место
Теорема. Итерационный процесс Зейделя для приведенной системы (3), эквивалентной нормальной системе (2), всегда сходится к единственному решению этой системы при любом выборе начального приближения.
Пример:
Х1 + Х2 + Хз = 3
Х1 + Х2 + Хз = 4
Х1 а+ 3 Х2 + Хз =5.
Для заданной системы:

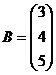
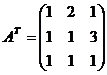
Вычислим:


Таким образом, нормальная система, полученная из заданной системы, имеет вид:
6x1 + 6х2 + 4хз = 16
6x1 + 11х2 + 5хз = 22
4x1 + 5 х2 + 3хз = 12
Приведенная система, эквивалентная этой нормальной системе, будет выглядеть так:
x1 а= - х2 - 0,7хз + 2,7
х2 = - 0,5455x1 - 0,4545хз +2
хз = - 1,x1 - 1,7х2 + 4
Коэффициенты приведенной системы вычислены по формулам (4) с точностью до четвертого знака после запятой. Отметим, что точное решение исходной системы таково: x1 = l, х2 = 1, хз = 1.
Расчетные формулы итерационного процесса Зейделя для данного конкретного случая будут иметь такой вид:
Y1 = - X2 - 0,7хз + 2,7
У2 = - 0,5455Y1 - 0,4545хз + 2
У3 = - 1,Y1 - 1,У2 + 4
Окончанием итерационного процесса будем считать момент, когда для всех пар соответствующих значений в двух последовательных приближениях будет выполняться соотношение:
|yi - xi |< Е, (i =1, 2, 3), где Е заданная точность вычислений
Для начальных значений 2.7; 2; 4 (близких к свободным членам системы) и Е = 0.1 результат работы программы будет таким:
X1 = 0.
Х2 = 1.
Х3 = 1.2
Теперь мы можем наметить основные шаги алгоритма решения методом Зейделя произвольной системы линейных равнений.
1. Ввод матрицы А коэффициентов исходной системы и матрицы-столбца В ее свободных членов.
2. Ввод точности вычислений Е.
3. Вычисление транспонированной матрицы AT и матриц C=ATA и D=ATB нормальной системы.
4. Приведение нормальной системы к виду, допускающему осуществление итерационного процесса Зейделя (по формулам).
5. Циклическое осуществление итерационного процесса с вычислением наибольшего значения разности между соответствующими значениями неизвестных в последовательных приближениях (обозначение этого наибольшего значения М).
6. Выход из итерационного процесса при М<Е и печать значений неизвестных, соответствующих последнему полученному приближению.
Лабораторная работа № 14
Расчет цепи постоянного тока
Цель: меть вести расчет цепи постоянного тока по методу Зейделя.
Задание: Дана линейная электрическая цепь (см. лаб. № 13).
Варианты заданий
Определить все токи в ветвях методом Зейделя с точностью до 0.001.
1. 2.7x1+3.3x2+1.3x3=2.1; 16. 3.8x1+4.1x2-2.3x3=4.8;
3.5x1-1.7x2+2.8x3=1.7; -2.1x1+3.9x2-5.8x3=3.3;
4.1x1+5.8x2-1.7x3=0.8. 1.8x1+1.1x2-2.1x3=5.8.
2. 1.7x1+2.8x2+1.9x3=0.7; 17. 1.7x1-2.2x2+3.0x3=1.8;
2.1x1+3.4x2+1.8x3=1.1; 2.1x1+1.9x2-2.3x3=2.8;
4.2x1-1.7x2+1.3x3=2.8. 4.2x1+3.9x2-3.1x3=5.1.
3. 3.1x1+2.8x2+1.9x3=0.2; 18. 2.8x1+3.8x2-3.2x3=4.5;
1.9x1+3.1x2+2.1x3=2.1; 2.5x1-2.8x2+3.3x3=7.1;
7.5x1+3.8x2+4.8x3=5.6. 6.5x1-7.1x2+4.8x3=6.3.
4. 9.1x1+5.6x2+7.8x3=9.8; а19. 3.3x1+3.7x2+4.2x3=5.8;
3.8x1+5.1x2+2.8x3=6.7; 2.7x1+2.3x2-2.9x3=6.1;
4.1x1+5.7x2+1.2x3=5.8. 4.1x1+4.8x2-5.0x3=7.0.
5. 3.3x1+2.1x2+2.8x3=0.8; 20. 7.1x1+6.8x2+6.1x3=7.0;
4.1x1+3.7x2+4.8x3=5.7; 5.0x1+4.8x2+5.3x3=6.1;
2.7x1+1.8x2+1.1x3=3.2. 8.2x1+7.8x2+7.1x3=5.8.
6. 7.6x1+5.8x2+4.7x3=10.1; 21. 3.7x1+3.1x2+4.0x3=5.0;
3.8x1+4.1x2+2.7x3=9.7; 4.1x1+4.5x2-4.8x3=4.9;
2.9x1+2.1x2+3.8x3=7.8. -2.1x1-3.7x2+1.8x3=2.7.
7. 3.2x1-2.5x2+3.7x3=6.5; 22. 4.1x1+5.2x2-5.8x3=7.0;
0.5x1+0.34x2+1.7x3=-0.24 3.8x1-3.1x2+4.0x3=5.3;
1.6x1+2.3x2-1.5x3=4.3. 7.8x1+5.3x2-6.3x3=5.8.
8. 5.4x1-2.3x2+3.4x3=-3.5; 23. 3.7x1-2.3x2+4.5x3=2.4;
4.2x1+1.7x2-2.3x3=2.7; 2.5x1+4.7x2-7.8x3=3.5;
3.4x1+2.4x2+7.4x3=1.9. 1.6x1+5.3x2+1.3x3=-2.4.
9. 3.6x1+1.8x2-4.7x3=3.8; 24. 6.3x1+5.2x2-0.6x3=1.5;
2.7x1-3.6x2+1.9x3=0.4; 3.4x1-2.3x2+3.4x3=2.7;
1.5x1+4.5x2+3.3x3=-1.6. 0.8x1+1.4x2+3.5x3=-2.3.
10. 5.6x1+2.7x2-1.7x3=1.9; 25. 1.5x1+2.3x2-3.7x3=4.5;
3.4x1-3.6x2-6.7x3=-2.4; 2.8x1+3.4x2+5.8x3=-3.2;
0.8x1+1.3x2+3.7x3=1.2. 1.2x1+7.3x2-2.3x3=5.6.
11. 2.7x1+0.9x2-1.5x3=3.5; 26. 0.9x1+2.7x2-3.8x3=2.4;
4.5x1-2.8x2+6.7x3=2.6; 2.5x1+5.8x2-0.5x3=3.5;
5.1x1+3.7x2-1.4x3=-0.14. 4.5x1-2.1x2+3.2x3=-1.2.
12. 4.5x1-3.5x2+7.4x3=2.5; 27. 2.4x1+2.5x2-2.9x3=4.5;
3.1x1-0.6x2-2.3x3=-1.5; 0.8x1+3.5x2-1.4x3=3.2;
0.8x1+7.4x2-0.5x3=6.4. а1.5x1-2.3x2+8.6x3=-5.5.
13. 3.8x1+6.7x2-1.2x3=5.2; 28. 5.4x1-2.4x2+3.8x3=5.5;
6.4x1+1.3x2-2.7x3=3.8; 2.5x1+6.8x2-1.1x3=4.3;
2.4x1-4.5x2+3.5x3=-0.6. 2.7x1-0.6x2+1.5x3=-3.5.
14. 5.4x1-6.2x2-0.5x3=0.52; 29. 2.4x1+3.7x2-8.3x3=2.3;
3.4x1+2.3x2+0.8x3=-0.8; 1.8x1+4.3x2+1.2x3=-1.2;
2.4x1-1.1x2+3.8x3=1.8. 3.4x1-2.3x2+5.2x3=3.5.
15. 7.8x1+5.3x2+4.8x3=1.8; 30. 3.2x1-11.5x2+3.8x3=2.8;
3.3x1+1.1x2+1.8x3=2.3; 0.8x1+1.3x2-6.4x3=-6.5;
4.5x1+3.3x2+2.8x3=3.4. 2.4x1+7.2x2-1.2x3=4.5.
Пример выполнения задания.
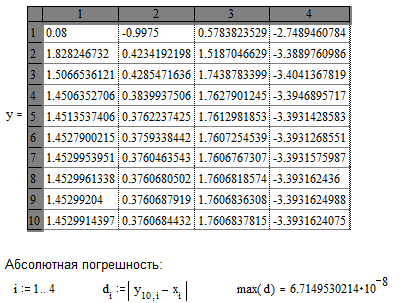
Пример. Дана система равнений Ax=b. Найти решение системы с помощью метода Зейделя, выполнив 10 итераций. Найти величину абсолютной погрешности итерационного решения.
Программа на MathCade имеет следующий вид:



a) Проверка достаточного словия сходимости метода Зейделя

Достаточное словие выполнено.


Результат работы функции zeid - 10 первых приближений 
з4. Решение системы линейных равнений методом итерации
При большом числе неизвестных линейной системы схема метода Гаусса, дающая точное решение, становится весьма сложной. В этих условиях для нахождения корней системы иногда добнее пользоваться приближенными численными методами. Изложим здесь один из этих методов - метод итерации.
Пусть дана линейная система
 а(1)
а(1)
Введя в рассмотрение матрицы



систему (1) коротко можно записать в виде матричного уравнения
х = В (Т)
Предполагая, что диагональные коэффициенты aii ¹ 0 ( i = 1, 2, Е, n), разрешим первое равнение системы (1) относительно х1, второе относительно х2 и т. д. Тогда получим эквивалентную систему
 (2)
(2)
где

 и aij = 0 при i = j (i,
j = 1, 2,..., n).
и aij = 0 при i = j (i,
j = 1, 2,..., n).
Введя матрицы
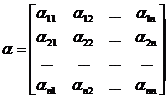 и
и 
систему (2) можем записать в матричной форме x = b + ax (Т)
Систему (2) будем решать методом последовательных приближений. За нулевое приближение принимаем, столбец свободных членов x0 = b.
Далее, последовательно строим матрицы-столбцы
x1 = b + a x0а (первое приближение),
X2 = b + a x1 (второе приближение) и т. д.
(k + 1) - е приближение вычисляют по формуле Xk+1 = b + a xk (k = 0, 1, 2,Е).
Если последовательность приближений x0, x1, Е, xk Е имеет предел, 
Метод последовательных приближений, определяемых формулой (3), носит название метода итерации. Процесс итерации (3) хорошо сходится, т.е. число приближений, необходимых для получения корней системы (1) с заданной точностью, невелико, если элементы матрицы a малы по абсолютной величине. Иными словами, для спешного применения процесса итерации модули диагональных -коэффициентов системы (1) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют).
Пример 1. Решить систему методом итерации.
 а (4)
а (4)
Решение. Здесь диагональные коэффициенты 4; 3; 4 системы значительно преобладают над остальными коэффициентами при неизвестных. Приведем эту систему к нормальному виду (2)
Х1 = 2 - 0.06х2 + 0.02х3
Х2 = 3 - 0.03х1 + 0.05х3 (5)
Х3 = 5 - 0.01х1 + 0.02х2
В матричной форме систему (5) можно записать так:
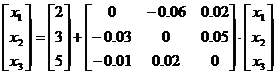
За нулевые приближения корней системы (4)
принимаем:  а
а а
а
Подставляя эти значения в правые части равнений (5), получим первые приближения корней:
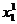 а= 2 - 0,06*3 + 0,02*5 = 1,92
а= 2 - 0,06*3 + 0,02*5 = 1,92
 а=3 - 0,03*2 + 0,05*5 = 3,19
а=3 - 0,03*2 + 0,05*5 = 3,19
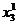 а= 5 - 0,01*2 +0,02*3 = 5,04
а= 5 - 0,01*2 +0,02*3 = 5,04
Далее, подставляя эти найденные приближения в формулу (5) получим вторые приближения корней:
 а
а  а
а
После новой подстановки будем иметь третьи приближения корней: 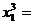 1,90923;
1,90923;
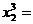 а3,19495;
а3,19495; 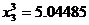 . Замечание. При применении метода итерации (формула (3)) нет необходимости за нулевое приближение X0 принимать столбец свободных членов. Cходимость процесса итерации зависит только от свойств матрицы a, причем при выполнении известных словий, если этот процесс сходится при каком-нибудь выборе исходного начального приближения, то он будет сходиться к тому же предельному вектору и при любом другом выборе этого начального приближения.
Поэтому начальный вектор x0 в процессе итерации может быть взят произвольным.
. Замечание. При применении метода итерации (формула (3)) нет необходимости за нулевое приближение X0 принимать столбец свободных членов. Cходимость процесса итерации зависит только от свойств матрицы a, причем при выполнении известных словий, если этот процесс сходится при каком-нибудь выборе исходного начального приближения, то он будет сходиться к тому же предельному вектору и при любом другом выборе этого начального приближения.
Поэтому начальный вектор x0 в процессе итерации может быть взят произвольным.
Достаточное условие сходимости.
Если для приведенной системы (2) выполнено по меньшей мере одно из словий:
1.  (i = 1, 2, Е, n)
(i = 1, 2, Е, n)
или
2.
а (j = 1, 2, Е, n)
(j = 1, 2, Е, n)
то процесс итерации (3) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Лабораторная работа №15
Расчет цепи постоянного тока
Цель: меть вести расчет цепи постоянного тока по методу итерации.
Задание: Дана линейная электрическая цепь (см. лаб. № 13).
Варианты заданий
Определить все токи в ветвях методом итерации с точностью до 0.001.
Номер Матрица системы Правая
вари-
нт
1 2 3
---------------------------------------------------------
1.4 .3.8.0014 .1220
-.0029 -.5 -.0018 -.0012 -.2532
-.0055 -.0050 -1.4 -.0039 -.9876
-.0082 -.0076 -.0070 -2.3 -2.0812
2а 1.7 .3.4.5 .6810
..8.1.2 .4803
-.3 -.2 -.1 . -.0802
-.5 -.4 -.3 -1. -1.7
3а 3. .0038.0049.0059 1.5136
.0011 2.1.0032 .0043 1.4782
-.5.5 1.2.0026 1.0830
-.0022 -.0011 -.1 .3.3280
4а 4.3 .0217.0270.0324 2.6632
.0100 3.4.0207 .0260 2.9
.0037.0090 2.5 .0197 2.5330
-.0027.0027.0080 1.6 1.9285
5а 5.6 .0268.0331.0393 4.0316
.0147 4.7.0271 .0334 4.3135
.0087.0150 3.8 .0274 4.2353
а.0028 .0090.0153 2.9 3.7969
6а 6.9 .0319.0390.0416 5.6632
.0191 6..0 .0405 6.9
.0134.0205 5.1 .0348 6.2
.0077.0149.0220 4.2 5.9275
7а 8.2 .0370.0451.0532 7.5591
.0234 7.3.0396 .0477 8.1741
.0179.0260 6.4 .0422 8.4281
.0124.0205.0286 5.5 8.3210
8а 9.5 .0422.0513.0604 9.7191
.0278 8.6.0459 .0550 10.5
.0224.0315 7.7 .0496 10.9195
9 10.8.0475.0576 .0676а 12.1430
.0321 9.9.0523.0623а 13.0897
.0268.0369 9. .0570а 13.6744
.0215.0316.0416 8.1а 13.8972
10 12.1.0528.0639 .0749а 14.8310
.0365 11.2.0586 .0697а 15.9430
.0312 .0423а 10.3.0644а 16.6926
.0260.0370.0481 9.4а 17.0800
11 13.4.0518.0702 .0822а 17.7828
.0408 12.5.0650 .0770а 19.0599
.0356.0477а 11.6 .0718а 19.9744
.0304.0425.0546 10.7а 20.5261
12 14.7.0635.0765 .0896а 20.9985
.0452 13.8.0714 .0844а 22.4406
.0400.0531а 12.9 .0793а 23.5195
.0349.0479.0610 12. 24.2353
13 16..0688 .0829.0970а 24.4781
.0496 15.1.0 .0918а 26.0849
.0.0585а 14.2 .0867а 27.3281
.0393.0534.0674 13.3а 28.2078
14 17.3.0741 .0892.1043а 28.2215
.0539 16.4.0841 .0992а 29.9928
.0488.0639а 15.5 .0941а 31.4001
.0437.0588.0739 14.6 а32.4435
15 23.8.1010 .1212.1414а 50.8968
.0757 22.9.1161 .1363а 53.4873
.0707.0909а 22. .1313а 55.7118
.0656.0858.1060 1.1а 57.5703
16 19..0849 .1020.1191а 36.5001
.0626 19..0969 .1140а 38.5997
.0576.0747а 18.1 .1090а 40.3345
.0525.0696.0867 17.2а 41.7045
17 21.2.0902.1084 .1265а 41.0351
.0670 20.3.1033 .1215а 41.2986
.0619.0801а 19.4 .1164а 45.1968
.0569.0750.0932 18.5а 46.7299
18 22.5.0956.1148 .1339а 45.8340
.0714а 21.6 .1097.1289а 48.2611
.0663.0855а 20.7 .1238а 50.3226
.0612.0804.0996 19.8а 52.0184
19 23.8.1010.1212 .1414а 50.8968
.0757 22.9.1161 а.1363а 53.4873
.0707.0909а 22. .1313а 55.7118
.0656.0858.1060 21.1а 57.5703
20 25.1.1063.1276 .1488а 56.2234
.0801 24.2.1225 .1437а 58.9772
а.0750 .0963а 23.3.1387а 61.3645
.0700.0912.1124 22.4а 63.3853
21 26.4.7.1339 .1562а 61.8139
.0844 25.5.1289 .1512а 64.7307
.0794.1017а 24.6 .1461а 67.2806
.0744.0966.1189 23.7а 69.4636
22 27.7.1171 .1403.1636а 67.6682
.0 26.8.1353 .1586а 70.7478
.0838.1070а 25.9 .1536а 73.4601
.0788.1020.1253 25. 75.8051
23 29..1225.1467 .1710а 73.7864
.0932 28.1.1417 .1660а 77.0286
.0882.1124а 22.2 .1610а 79.9030
.0831.1074.1317 26.3а 82.4098
24 30.3.1278.1531 .1784а 80.1684
.0975 29.4.1481 .1734а 83.5730
.0925.1178а 28.5 .1684а 86.6095
.0875.1128.1381 27.6а 89.2778
25 31.6.1332 .1595.1859а 86.8143
.1019 30.7.1545 .1809а 90.3811
.0969.1232а 29.8 .1759а 93.5793
.0919.1182.1445 28.9а 96.4090
26 32.9.1386 .1659.1933а 93.7240
.1062 32..1610 .1883а 97.4528
.1013.1286а 31.1 .1833 100.8126
.0963.1236.1510 30.2 103.8034
27 34.2.1400.1724 .2007 100.8976
.1106 33.3.1674 .1957 104.7881
.1056.1340а 32.4 .1907 108.3093
.1006.1290.1574 31.5.4610
28 35.5.1494.1788 .2082 108.3351
.1150 34.6 .1738.2032 112.3871
.1100.1394а 33.7 .1982 116.0694
.1050.1344.1638 32.8 119.3819
29 36.8.1547.1852 .2156 116.0363
.1193 35.9.1802 .2106 120.2497
.1143.1448а 35. .2056 124.0930
.1094.1398.1702 31.1 127.5660
30 38.1.1601.1916 .2230 124.0015
.1237 37.2.1866 .2180 128.3760
.1187.1502а 36.3.2131 132.3800
.1137.1452.1766 35.4 136.0134
Пример выполнения работы
Программа на MathCade имеет следующий вид:
|
Пример. Решение системы равнений методом простой итерации |
|
Пусть дана система равнений Ax = b |
|
|
|
|
|
Для построения итерационного процесса найдем собственные числа матрицы A |
|
|
|
|
|
Вычислим итерационный параметр и проверим словие сходимости |
|
|
|
|
|
|
|
|
Возьмем начальное приближение - вектор x0, зададим точность 0.001 и найдем начальные приближения по приведенной ниже программе: |
|
|
|
|
|
|
|
|
|
Точное решение |
|
|
|
з 5. Применение метода Гаусса для вычисления определителей
Пусть

(1)
D = det Aа (2)
Рассмотрим линейную систему Ах=0. (3)
 А треугольной матрицей В, состоящей из элементов отмеченных строк.
А треугольной матрицей В, состоящей из элементов отмеченных строк.
В результате получалась эквивалентная система
Bx = 0 (4)
Элементы матрицы В последовательно получались из элементов матрицы А и дальнейших вспомогательных матриц А1, А2,..., An-1 с помощью следующих элементарных преобразований:
1) деления на ведущие элементы А11, А22,..., Ann, которые предполагались отличными от нуля,
2) вычитания из строк матрицы А и промежуточных матриц Аi (i=1, 2,..., n-1) чисел, пропорциональных элементам соответствующих ведущих строк. При первой операции определитель матрицы также делится на соответствующий ведущий элемент, при второйЧопределитель матрицы остается неизменным. Поэтому
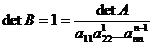
Следовательно,
Δ = det A =  (5)
(5)
т, е. определитель равен произведению ведущих элементов для соответствующей схемы Гаусса. Отсюда заключаем, что схема единственного деления может быть использована для вычисления определителей, причем столбец свободных членов тогда становится излишним.
Заметим, что если для какого-нибудь шага элемент аii=0 или близок к нулю (что влечет за собой меньшение точности вычислений), то следует соответствующим образом изменить порядок строк и столбцов матрицы.
Пример. Вычислить определитель
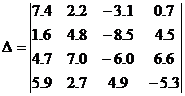
Решая по методу Гаусса, находим ведущие элементы, получим:
D = 7.4*4.32434*6.11331*(-7.58393) = - 1483.61867
з 6. Вычисление обратной матрицы методом Гаусса.
Пусть дана неособенная матрица
A=[a ij] (i, j = 1,2, Е, n)а (1)
Для нахождения ее обратной матрицы
-1 = [x ij] (2)
используем основное соотношение
AA-1 = E (3)
где Чединичная матрица.
Перемножая матрицы А и А-1, будем иметь n систем равнений относительно n2 неизвестных x ij
 а (i, j = 1, 2, Е,n)
а (i, j = 1, 2, Е,n)
где

Полученные n систем линейных равнений для j = 1, 2,..., n, имеющих одну и ту же матрицу А и различные свободные члены, одновременно можно решить методом Гаусса.
Пример. Найти обратную матрицу A-1 для матрицы

A=
Решение. Составим схему с единственным делением. Заметим, что элементы строк обратной матрицы получаются в обратном порядке. Находим обратную матрицу

A-1=
Для проверки составим произведение


|
|
|
 |
|
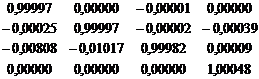 |
|
Мы видим, что благодаря округлению обратная матрица получилась не вполне точной.
з 7. Метод квадратных корней
Пусть дана линейная система
х =В (1)
где A=[аij] Чсимметрическая матрица, т.е. A'=[Aij]=A. Тогда матрицу А можно представить в виде произведения двух транспонированных между собой треугольных матрица А = Т'*Т (2),
где
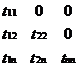
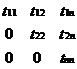 T = и TТ =
T = и TТ =
Производя перемножение матриц Т и T', для определения элементов tij матрицы Т получим следующие равнения:
t1it1j+t2it2j+Е+tiitjj = aij (i < j)
t1i2 + t2i2а +Е+ tii2 = aii
Отсюда последовательно находим:
 (3)
(3) 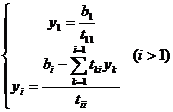 (4)
(4)
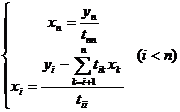 (5)
(5)
Изложенный способ решения линейной системы носит название метода квадратных корней. При прямом ходе с помощью с помощью формул (3) и (4) последовательно вычисляются коэффициенты tij и yi (i = 1, 2,Е, n), затем обратным ходом с помощью формулы (5) находятся неизвестные xi (i = n, n - 1, Е, 1).
Пример. Решить систему равнений с помощью метода квадратных корней.

Применяя формулы (3) и (4), последовательно переходя от строки к строке, вычисляем коэффициенты tij и новые свободные члены yi. Например

на основании формул (5) находим значения неизвестных xi , например
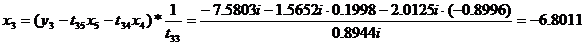 а
а
з 8. Метод скорейшего спуска (градиента) для случая системы линейных алгебраических равнений
В рассматриваемом ниже итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге (максимально приблизиться к корню).
Представим систему линейных равнений в следующем виде:
 (1)
(1)
Запишем выражение (1) в операторной форме:
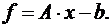 (2)
(2)
Здесь приняты следующие обозначения:


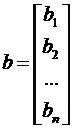 (3)
(3)
В методе скорейшего спуска решение ищут в виде
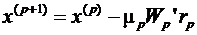 (4)
(4)
где  аи
аи  а- векторы неизвестных на p и p+1 шагах итераций; вектор невязок на p-ом шаге определяется выражением
а- векторы неизвестных на p и p+1 шагах итераций; вектор невязок на p-ом шаге определяется выражением
 (5)
(5)
 а (6)
а (6)
В формуле (6) используется скалярное произведение двух векторов, которое определяется следующей формулой:
 (7)
(7)
В формуле (6)  p-ом шаге. Матрица Якоби вектор - функции f(x) определяется как
p-ом шаге. Матрица Якоби вектор - функции f(x) определяется как
 (8)
(8)
Нетрудно убедиться, что для системы (2) матрица Якоби равна
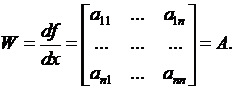 (9)
(9)
Как и для метода простой итерации, достаточным словием сходимости метода градиента является преобладание диагональных элементов. В качестве нулевого приближения можно взять 
-Как видно из выражения (8), матрица Якоби не зависит от шага итерации.
-Требования минимизации погрешности на каждом шаге обусловили то, что метод градиента более сложен (трудоемок), чем методы Якоби и Зейделя.
-В методе градиента итерационный процесс естественно закончить при достижении 
В приближенных методах можно обеспечить практически любую погрешность, если итерационный процесс сходится.
Итерационный процесс можно прервать на любом kЦом шаге и продолжить позднее, введя в качестве нулевого шага значения x(k).
В качестве недостатка приближенных методов можно отметить то, что они часто расходятся, достаточные словия сходимости (преобладание диагональных элементов) можно обеспечить только для небольших система из 3 - 6 равнений.
Пример. Методом скорейшего спуска решим систему равнений

Так как диагональные элементы матрицы являются преобладающими, то в качестве начального приближения выберем:

Следовательно, вектор невязок на нулевом шаге равен

Далее последовательно вычисляем
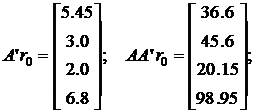
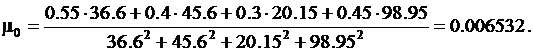
Отсюда 
причем

налогично находятся последующие приближения и оцениваются невязки. Что касается данного примера, можно отметить, что итерационный процесс сходится достаточно медленно (невязки меньшаются).
Вопросы для самопроверки
1.
2.
3.
4.
5.
6.
7.
8.
)а начального приближения (нулевой итерации);
б)а первой итерации?
10. При решении СЛАУ (n > 100) итерационными методами решение расходится. Как найти начальное приближение?
11. В чем основное отличие точных и приближенных методов решения систем линейных равнений?
12. Каким методом лучше всего решать систему равнений невысокого порядка, например третьего?
13. В каких случаях предпочтительны итерационные методы решения систем линейных равнений?
14. От чего зависит скорость сходимости метода итераций?
15. Можно ли получить решение системы высокой размерности с погрешностью не хуже заданной?
16. Каким образом в методе Гаусса можно контролировать накопление вычислительных ошибок?
17. К точным или приближенным методам относится метод Крамера?
18. При каком словии будет сходиться метод итераций?
19. Можно ли заранее оценить число итераций для получения решения с заданной погрешностью?
20. Как влияет вычислительная ошибка на точность решения системы равнений методом итераций?
Ответы:
11. Точные методы решения систем линейных равнений позволяют получить решение непосредственно в аналитическом виде или в виде алгоритма с конечным числом шагов, приближенные Ч как предел некоторой последовательности при стремлении числа итераций к бесконечности.
12. Систему из трех равнений, конечно, проще всего решать любым точным методом, например методом Крамера.
13. Итерационные методы наиболее предпочтительны в задачах высокой размерности, когда точные методы могут дать решение с большой накопившейся вычислительной погрешностью.
14. Скорость сходимости в методе итераций зависит от свойств системы уравнений (определяющейся коэффициентами равнений) и от начальных словий поиска решения.
15. Если размерность задачи высока, то получить решение с погрешностью не хуже заданной точным методом невозможно, так как нет приемов коррекции накапливающихся вычислительных ошибок, становящихся значительными при большом числе вычислений, есть только приемы их контроля.
16.В методе Гаусса можно ввести дополнительные переменные в каждом равнении, равные сумме всех коэффициентов уравнения, с которыми проводят все операции как с коэффициентами. При этом невыполнение равенства этих переменных сумме коэффициентов является признаком накопившейся вычислительной погрешности.
17.Метод Крамера относится к точным методам.
18.Метод итераций будет сходиться, если все суммы модулей коэффициентов строк (или столбцов) преобразованной системы равнений будут меньше единицы.
19.Число шагов для получения решения с заданной погрешностью можно оценить заранее, используя выражение для погрешности. Для этого надо подставить в выражение заданное значение погрешности и решить получающееся равнение относительно числа итераций (оно находится в показателе степени).
20. Наличие вычислительной ошибки в итерационных методах приводит лишь к величению числа итераций для достижения решения, так как итерационные методы обладают свойством самоисправляемости ошибок.
Глава 5. Приближённое решение систем нелинейных равнений
з 1. Метод Ньютона
Рассмотрим, вообще говоря, нелинейную систему равнений
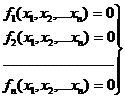 (1)
(1)
с действительными левыми частями.
Запишем короче систему (1). Совокупность аргументова x1,x2,Еxnа можно рассматривать как n-вектор

налогично совокупность функций f1,f2,Е,fn представляет собой также n-мерный вектор (вектор-функцию)

Поэтому система (1) кратко записывает так: f(x)=0 (1')
Для решения системы (1') будем пользоваться методом последовательных приближений.
Предположим, что найдено р-е приближение
x(p)=(x1(p),x2(p),Еxn(p))
одного из изолированных корней x=(x1,x2,Еxn) векторного уравнения (1') можно представить в виде
x=x(p)+ε(p)
где ε(p)=(ε1(p),ε2(p),Еεn(p)) - поправка (погрешность корня). Подставляя выражение (2) в равнение (1'), будем иметь:
f(x(p) +ε(p))=0. (3)
Предполагая, что функция f(x) непрерывно дифференцируема в некоторой выпуклой области, содержащей x и x(p), разложим левую часть равнения (3) по степеням малого вектора ε(p), ограничиваясь линейными членами,
f(x(P)+ε(p))=f(x(p))+f''''(x(p))ε(p)=0. (4)
или, в развёрнутом виде,ε

Из формул (4) и (4' ') вытекает, что под производной f''(x) следует понимать матрицу Якоби системы функцийа
f'1,f2,Е,fnа относительно переменных x1,x2,Е,xn, т.е.

или в краткой записи
 (i,j=1,2,Е,n).
(i,j=1,2,Е,n).
Система (4 ')
представляет собой линейную систему относительно поправок  (i=1,2,..,n) с матрицей W(x), поэтому формула (4) может быть записана в следующем виде:
(i=1,2,..,n) с матрицей W(x), поэтому формула (4) может быть записана в следующем виде:
f(x(p))+W(x(p))ε(p)=0.
Отсюда, предполагая, что матриц W(x(p))- неособенная, получим :
ε(p)=-W-1(x(p))ε(p).
Следовательно,
x(p+1)=x(p)-W-1(x(p))f(x(p)) (p=0,1,2,Е) (5)
(метод Ньютона ).
За нулевое приближение x(0) можно взять грубое значение искомого корня.
Пример 1. Приближенно найти положительные решения системы равнений
 (6)
(6)
Решение. Кривые, определяемые системой (6), пересекаются приблизительно в точках M1(1,4;-1,5) и M2(3,4;2,2). Исходя из начального приближения
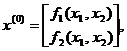
имеем :

Составим теперь матрицу Якоби

где М=0,43429. Отсюда
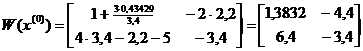
причем
Δ=detW(x(0))=23,4571.
Следовательно, матрица W(x(0))-неособенная. Составим обратную ей матрицу
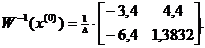
Используя формулу (5), получим :
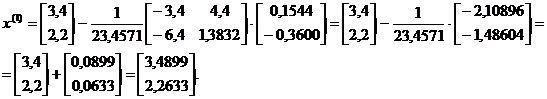
Решение: Имеем:

Отсюда:

Составим матрицу Якоби

Имеем
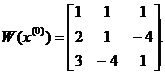
и

Находим обратную матрицу

По формуле (5) получаем первое приближение

Далее вычисляем второе приближение x(2). Имеем:
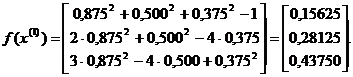
и

Отсюда

и

Используя формулу (5), получаем:
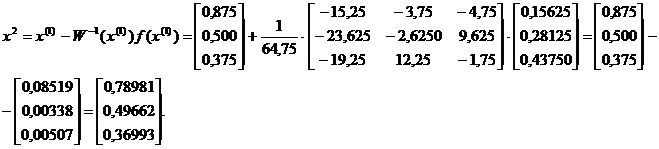 а Аналогично находятся дальнейшие приближения:
а Аналогично находятся дальнейшие приближения:
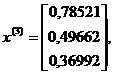

и т.д.
Ограничиваясь третьим приближением, получим:
x= 0,7852; y= 0,4966; z= 0,3699.
з 2. Метод градиента (метод скорейшего спуска)
Пусть имеется система нелинейных равнений:
 (1)
(1)
Систему (1) добнее записать в матричном виде:
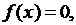 (2)
(2)
где 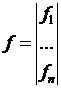 а- вектор - функция;
а- вектор - функция; 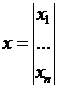
Решение системы (2), как и для системы линейных уравнений, будем искать в виде
 (3)
(3)
Здесь  аи
аи  а- векторы неизвестных на p и p+1
шагах итераций; вектор невязок на p-ом шаге - f(p) = f(x(p));
W'p - транспонированная матрица Якоби на p - ом шаге;
а- векторы неизвестных на p и p+1
шагах итераций; вектор невязок на p-ом шаге - f(p) = f(x(p));
W'p - транспонированная матрица Якоби на p - ом шаге;


Пример. Методом градиента вычислим приближенно корни системы


расположенные в окрестности начала координат.
Имеем:

Выберем начальное приближение:
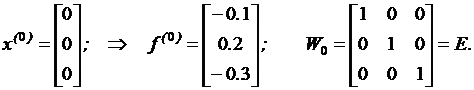
По выше приведенным формулам найдем первое приближение:
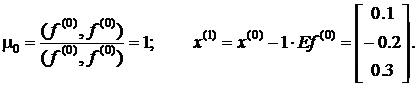
налогичным образом находим следующее приближение:


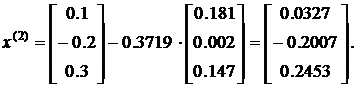
Ограничимся двумя итерациями (шагами), и оценим невязку:
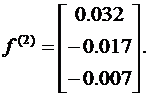
Как видно из примера, решение достаточно быстро сходится, невязка быстро убывает.
При решении системы нелинейных равнений методом градиента матрицу Якоби необходимо пересчитывать на каждом шаге (итерации).
Лабораторная работа № 16
Нелинейные равнения
Цель:а Научиться решать нелинейные равнения методом Ньютона и градиента.
Задание: Решить систему нелинейных равнений методом градиента и методом Ньютона с точностью e, выполнить вычисления на персональнома компьютере.
Варианты заданий
№ вар
Система равнений
точность e
1.
x1=0,5sin(0,3 x2)+2; x2= 0,5cos(0,3x1)
10-4
2.
x1=0,5sin(0,2 x2)+2; x2= 0,5cos(0,5x1)
10-5
3.
x1=0,5sin(0,2 x2)+3; x2= 0,5cos(0,5x1)
10-5
4.
x1= 0,25sin(0,3 x2) +2 ; x2= cos(0,3x1)
10-3
5.
x1=0,25sin(0,3 x2)+3; x2= 0,1cos(0,25x1)
10-4
6.
x1=0,5sin(0,3 x2)+1; x2= 0,2cos(0,25x1)
10-4
7.
x1=0,5sin(0,2 x2)+3; x2= 0,3cos(0,25x1)
10-5
8.
x1=0,25sin(0,3 x2)+1; x2= 0,5cos(0,3x1)
10-3
9.
x1=0,5sin(0,3 x2)+2; x2= 0,5cos(0,5x1)
10-4
10
x1=0,25sin(0,3x2)+2; x2= 0,5cos(0,5x1)
10-3
Пример выполнения задания.
Пример. Найти с точностью 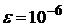

используя метод Ньютона для системы нелинейных равнений. Найти корни с помощью встроенного блока решения уравнений Givenа Findа пакета MATHCAD.
Программа на MathCade имеет следующий вид:
Уравнения системы:


Локализация корней:
Первое уравнение, разрешенное относительно x2:
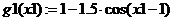
Второе уравнение, разрешенное относительно x2:
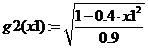
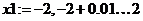
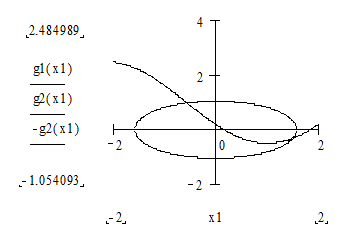
Первый корень:
Начальное приближение:


Точность для блока Given Find:
TOL:= 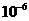
Решение системы f(x1,x2)=0 с помощью встроенного блока MATHCAD:
i. Given

 0
0
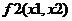
 0
0
 (
(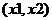
Полученное приближенное решение:

Вопросы для самопроверки
1.
2.
3.
4. Как проводится отделение корней при решении систем нелинейных равнений?
5. Почему после одного шага по методу Ньютона мы не попадаем в решение, хотя рассчитывали из словия попадания в решение?
6. От чего зависит скорость сходимости метода Ньютона?
7. Можно ли обеспечить сходимость метода итераций при решении систем нелинейных равнений?
8. Каким образом можно повысить точность решения системы нелинейных равнений?
9. Оказывает ли влияние на результат решения выбор начального приближения в методе итераций?
Метод градиента
1. При какома иза алгоритмова выбора направления поиска max F(х) метод будет более эффективен?
2. Как изменяется гол между двумя соседними направлениям поиска при приближении к оптимуму?
3. Что называется градиентом функции F(х1,х2)?
4. Свойства градиента функции F(x)
5. Как оценивается эффективность поиска градиентным методом?
6. Какой алгоритм коррекции шага предпочтительнее вблизи оптимума?
7. Почему в районе оптимума величина шага Dх бывает при использовании алгоритмах 
8. В чем отличие двух алгоритмов градиентного метода: 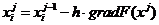
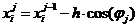
где  Ч направляющие косинусы градиента.
Ч направляющие косинусы градиента.
9. Исходя из определения grad F(x) как вектора, казывающего направление возрастания функции, что лучше искать: min или max?
10. Что дает вычисление производных по методу с парными пробами?
Метод наискорейшего спуска
1. В чем основные отличия метода наискорейшего спуска от метода градиента?
2. По какому направлению осуществляется поиск из каждой текущей точки при поиске min F(x)?
3. Как вычисляется градиент F(x) в методе наискорейшего спуска?
4. Почему после нахождения min F(x) по направлению необходимо еще раз искать min F(x) по другому направлению?
5. Каковы словия окончания поиска?
6. Область наивысшей эффективности метода.
7. Какой метод вычисления шага при поиске min F(x) по grad F(x) более предпочтителен?
8. Можно ли методом наискорейшего спуска найти max F(x)?
9. Можно ли применять алгоритм коррекции шага поиска, определяемый изменением гла между градиентами в текущей и предыдущей точках?
10. Какое влияние оказывают вычислительные погрешности при поиске min F(x) в направлении градиента на точность получения решения?
Метод сопряженных градиентов
1. Чем отличаются квадратичные методы оптимизации от линейных?
2. Какова сравнительная эффективность метода сопряженных градиентов и наискорейшего спуска вблизи от оптимума?
3. Как записывается алгоритм метода сопряженных градиентов?
4. Как влияют вычислительные погрешности на эффективность метода сопряженных градиентов?
5. Для каких функций F(х) метод сопряженных градиентов наиболее эффективен?
6. В чем недостатки использования методов второго порядка?
7. В чем отличие первого шага в методах наискорейшего спуска и сопряженных градиентов?
8. Какая процедура поиска осуществляется на каждом шаге?
9. Сравнительная эффективность метода градиента и метода сопряженных градиентов вдали от оптимума.
10. Возможно ли применение метода для не дифференцируемых функций?
Метод тяжелого шарика
1. Как влияет масса шарика на характер поиска, учитывая, что траектория поиска аналогична движению шарика в вязкой среде?
2. Может ли поиск ускоряться?
3. Можно ли найти max F(x), а не min F(x) методом тяжелого шарика?
4. В чем заключаются недостатки метода тяжелого шарика?
5. Является ли метод тяжелого шарика пригодным для одномерной оптимизации (т.е. когда у "шарика" нет объема, следовательно, и массы)?
6. Можно ли найти глобальный минимум F(х) методом тяжелого шарика?
7. Зачем "помещают шарик в вязкую среду"?
8. Какой путь можно выбрать для затухания поиска в районе оптимум при использовании алгоритма  grad F(х)?
grad F(х)?
9. Можно ли отнести метод тяжелого шарика к методам второго порядка?
10. В каких словиях предпочтительнее использовать метод тяжелого шарика?
Ответы:
4. Отделение корней при решении систем, как правило, не проводят, так как в общем случае это сделать крайне трудно или вообще невозможно.
5. Фактически при расчете величины шага в методе Ньютона - Рафсона нелинейные функции линеаризуются, вследствие этого и не получается в новой точке решения, она рассматривается лишь как приближение к решению, и метод приобретает итерационный характер.
6. Скорость сходимости метода Ньютона - Рафсона существенно зависит от выбора начального приближения.
7. Сходимость метода итераций можно обеспечить способом приведения к виду, удобному для итераций (подробнее см. соответствующий раздел книги).
8. Для повышения точности решения достаточно меньшить задаваемую погрешность, по достижении которой прекращается процесс решения.
9. Да, оказывает. Поскольку корни отделить практически невозможно, то выбор начальной точки поиска определяет корень, который будет найден; фактически перебирая различные начальные словия, можно находить разные корни, и если повезет, то даже все.
Метод градиента
1. При применении алгоритма с использованием направляющих косинусов поиск будет более эффективным, так как появляется возможность однозначно правлять величиной шага путем выбора
коэффициента пропорциональности шага. В исходном базовом алгоритме величина шага зависит еще и от величины модуля градиента, который трудно оценить заранее, хотя в этом случае по мере приближения к оптимуму шаг сам будет меньшаться за счет уменьшения градиента, в рекомендуемом методе необходимо применять специальные приемы.
2. Обычно гол между двумя соседними направлениями поиска при приближении к оптимуму меняется очень сильно, так как имеет место "проскок" экстремума при почти каждом шаге.
3. Градиентом функции F(х1, х2) называется вектор, который показывает направление и скорость возрастания функции; он может быть получен через свои проекции на оси координат, которые равны соответствующим частным производныма от F: grad F(х1, х2) = {дF/дх1, дF/дх2).
4. Основные свойства градиента вытекают из его определения: направление градиента совпадает с направлением самого крутого возрастания функции (именно поэтому его и применяют для определения направления движения к оптимуму), градиент всегда перпендикулярен линии ровня, проходящей через ту точку, в которой вычислен градиент, модуль градиента (т.е. величина градиента) характеризует скорость возрастания функции.
5. Эффективность поиска оценивается по числу повторов вычисления функции, экстремум которой ищется: чем меньше раз вычислялась функция для получения решения с заданной погрешностью, тем эффективнее поиск.
6. Вблизи оптимума предпочтение можно отдать алгоритму, в котором коэффициент пропорциональности шага меньшается вдвое при проскоке экстремума.
7. При использовании алгоритма  Цh*grad F(x) (знак
"минус"стоит в случае поиска минимума функции) величина шага Dх =h*grad F(x) бывает в районе оптимума вследствие меньшения градиента F(x) (в точке экстремума градиент равен нулю).
Цh*grad F(x) (знак
"минус"стоит в случае поиска минимума функции) величина шага Dх =h*grad F(x) бывает в районе оптимума вследствие меньшения градиента F(x) (в точке экстремума градиент равен нулю).
8. Отличие алгоритмов вычисления шага Dх = h*grad F(x) и Dх = h*cosj прежде всего заключается в отсутствии влияния величины градиента на величину шага во втором алгоритме, благодаря чему выбором коэффициента пропорциональности шага h можно однозначно правлять шагом, увеличивая вдали от оптимума или меньшая его вблизи оптимума.
9. При поиске максимума функции в алгоритме шага стоит знак "+" (ищем в направлении градиента), при поиске минимума - знак "-" (ищем в направлении, противоположном направлению градиента); в обоих случаях эффективность метода одинакова.
10. Вычисление градиента по методу с парными пробами, с одной стороны, худшает поиск (появляются дополнительные вычислительные затраты при определении частных производных); с другой стороны, лучшает поиск за счет более точного вычисления градиента.
Метод наискорейшего спуска
1. Основные ограничения метода наискорейшего спуска от метода градиента заключаются в том, что в методе градиента градиент вычисляется на каждом шаге, в методе наискорейшего спуска после одного вычисления градиента следует одномерный поиск оптимума по направлению градиента, т.е. делается несколько шагов при одном вычислении градиента.
2. При поиске минимума F(x) поиск из каждой точки осуществляется в направлении, противоположном направлению градиента в текущей точке.
3. Градиент в методе наискорейшего спуска вычисляется точно также, как и в методе градиента; способ вычисления градиента не зависит от метода поиска.
4. Направление градиента не остается постоянным в области поиска, поэтому экстремум в одном направлении не соответствует экстремуму функции, и требуется опять и опять искать оптимум по новым направлениям градиентов, пока не будет выполнено словие окончания поиска.
5. В качестве словия окончания поиска задается требуемая малость модуля градиента функции, т.е. должно выполняться словие |grad F(x)| £ e (в области оптимума градиент точно равен нулю, но достичь этого значения практически невозможно, можно лишь приблизиться сколь годно близко к нему).
6. Наиболее эффективен метод вдали от оптимума, особенно при отсутствии "оврагов" функции.
7. Даже при одноэкстремальной функции по направлению градиента может иметь место многоэкстремальность, что ограничивает применимость многих методов одномерного поиска; на практике чаще всего применяют метод последовательного сканирования до первого локального экстремума по направлению.
8. Конечно, можно найти максимум функции; название метода просто сохранило исторические корни происхождения метода, вид находимого экстремума зависит только от того, в какую сторону по градиенту совершаются рабочие шаги.
9. Нет, нельзя, так как два соседних направления поиска в методе наискорейшего спуска всегда ортогональны.
10. Влияние вычислительных погрешностей не очень существенно, оно приводит к не ортогональности следующего направления поиска и как следствие к некоторому замедлению поиска в целом.
Метод сопряженных градиентов
1. Квадратичные методы оптимизации от линейных отличаются использованием в алгоритме вторых производных (или двух предыдущих точек для расчета одной следующей) и, как следствие, более высокой скоростью сходимости к решению, также более сложным в реализации алгоритмом.
2. Метод сопряженных градиентов более эффективен, так как он относится к методам второго порядка.
3. Алгоритм метода записывается следующим образом: 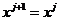 Цh*(grad F(
Цh*(grad F(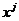 ) +a*grad F(
) +a*grad F(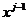 )).
)).
4. Влияние вычислительных погрешностей очень существенно: при их наличии поиск резко замедляется, так как они значительно искажают вторые производные (которые присутствуют в алгоритме косвенно).
5. Метод наиболее эффективен для квадратичных функций.
6. Необходимость прямо или косвенно вычислять вторые производные, которые очень чувствительны к различным погрешностям.
7. Различия в первом шаге методом наискорейшего спуска и методом сопряженных градиентов нет.
8. Ищется экстремум критерия в направлении поиска.
9. Эффективность методов вдали от оптимума примерно одинакова.
10. Нет, невозможно, так как метод предполагает нахождение производных для вычисления градиента.
Метод тяжелого шарика
1. "Масса шарика" увеличивает его инерционность, что приведет к колебаниям поиска в окрестности оптимума.
2. Да, поиск может скоряться, в этом основное достоинство метода. скорение происходит вследствие "разгона" шарика за счет его инерционности.
3. Можно найти любой вид экстремума, проведя коррекцию знаков в формулах рабочих шагов ("+" заменить на "-").
4. К недостаткам метода относят необходимость задания сразу двух параметров, определяющих эффективность поиска, влияние которых взаимосвязано.
5. Метод пригоден для задач любой размерности, но градиентные методы в одномерных задачах вырождаются, так как градиент всегда направлен по оси х.
6. Да, при дачном выборе двух параметров, определяющих эффективность метода, метод может остановиться в "глубоком" экстремуме. Это происходит за счет инерционности "шарика", вследствие которой он "выскакивает" из "мелких" локальных экстремумов.
7. "Помещение шарика в вязкую среду" способствует затуханию колебаний в районе оптимума.
8. В приведенном алгоритме 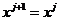 а-a(
а-a(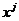 а-
а-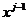 h*grad F(
h*grad F(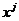 ) величина определяет
"память" алгоритма, т.е. учитывает влияние предыдущей точки, поэтому увеличение этого параметра метода может привести к более быстрому затуханию в районе оптимума, когда градиент функции мал.
) величина определяет
"память" алгоритма, т.е. учитывает влияние предыдущей точки, поэтому увеличение этого параметра метода может привести к более быстрому затуханию в районе оптимума, когда градиент функции мал.
9. Да, метод тяжелого шарика является методом второго порядка, так как новая точка поиска рассчитывается с использованием двух предыдущих.
10. Метод тяжелого шарика предпочтительно использовать при поиске экстремума многоэкстремальной функции с одним явно выраженным глобальным экстремумом и "мелкими" локальными, хотя он эффективно работает и при поиске экстремума одно экстремальных функций.
Глава 6. Интерполирование функций
з1. Введение
Если задана функция y(x), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоёмко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно. Функция у(х) может частвовать в каких-либо физико-технических или чисто математических расчётах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближённой формулой, то есть подобрать некоторую функцию j(х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х) j(х). Большая часть классического численного анализа основывается на приближении многочленами, так как с ними легко работать. Однако для многих целей используются и другие классы функций. Выбрав зловые точки и класс приближающих функций, мы должны ещё выбрать одну определённую функцию из этого класса посредством некоторого критерия - некоторой меры приближения или согласия.
Что касается критерия согласия, то классическим критерием согласия является точное совпадение в зловых точках. Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за погрешности, возникающей при измерении или вычислении значений в зловых точках.
Интерполяционные формулы применяются, прежде всего, при замене графически заданной функции аналитической, также для интерполяции в таблицах. Задачи интерполяции ва самома общема видеа можно сформулировать следующима образом. Пусть н отрезке [a,b]а заданы значения неизвестной функции y = f(x)а в nа различных точках:а x1, x2, Е,xn. Требуется найтиа многочлен Pа (x) степени n, приближенно выражающий функцию y =f (x) -а рис.1
 Поставленнуюа задачу можно решить используя различные интерполяционные формулы: Лагранжа, Ньютон и др.
Поставленнуюа задачу можно решить используя различные интерполяционные формулы: Лагранжа, Ньютон и др.
2.1. Метод Лагранжа
Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает значение 1 в одной зловой точке и 0 во всех других. Легко видеть, что функция
 (1)
(1)
является требуемым многочленом степени n; он равен 1, если x = xj
и 0, когда x =xi, i¹j. Многочлен Lj(x) yj принимает значения yi в i- й зловой точке и равен 0 во всех других злах. Из этого следует,
что 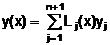 есть многочлен степени n,
проходящий через n+1 точку (xi, yi). Перепишим формулу (1) в виде:
есть многочлен степени n,
проходящий через n+1 точку (xi, yi). Перепишим формулу (1) в виде:
Ln(z)= 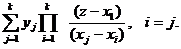 (2)
(2)
Где xi(i = Еk) - точки интерполяции;
yjа (j=Еk) - значения функции в точках интерполяции;
k - количество точек интерполяции;
z - значение аргумента, при котором нужно вычислить функцию
Формула (2) является основной для разработки алгоритма интерполяции заданной функции на ЭВМ.
Лабораторная работа № 17.
Интерполяционный многочлен Лагранжа
Цель: меть построить интерполяционный многочлен Лагранжа.
Задание: Для функции  ,
заданной таблицей своих значений, построить интерполяционные многочлены в форме Лагранжа. Используя их, вычислить приближенное значение функции в точке
,
заданной таблицей своих значений, построить интерполяционные многочлены в форме Лагранжа. Используя их, вычислить приближенное значение функции в точке 
Таблица к задаче
|
№ |
Таблица |
|
№ |
Таблица |
|
||||||||
|
1 |
x |
-2 |
-1 |
0 |
1 |
-1.25 |
16 |
x |
-3 |
-2 |
-1 |
0 |
-2.25 |
|
y |
4 |
1 |
-2 |
-3 |
y |
-2 |
-3 |
-1 |
0 |
||||
|
2 |
x |
-1 |
0 |
1 |
2 |
-0.25 |
17 |
x |
-2 |
-1 |
0 |
1 |
-1.25 |
|
y |
1 |
-2 |
-3 |
-1 |
y |
-3 |
-1 |
0 |
7 |
||||
|
3 |
x |
0 |
1 |
2 |
3 |
0.75 |
18 |
x |
-1 |
0 |
1 |
2 |
-0.25 |
|
y |
-2 |
-3 |
-1 |
0 |
y |
-1 |
0 |
7 |
4 |
||||
|
4 |
x |
1 |
2 |
3 |
4 |
1.75 |
19 |
x |
0 |
1 |
2 |
3 |
0.75 |
|
y |
-3 |
-1- |
0 |
7 |
y |
0 |
7 |
4 |
1 |
||||
|
5 |
x |
2 |
3 |
4 |
5 |
2.75 |
20 |
x |
-4 |
-3 |
-2 |
-1 |
-3.25 |
|
y |
-1 |
0 |
7 |
4 |
y |
-3 |
-1 |
0 |
7 |
||||
|
6 |
x |
3 |
4 |
5 |
6 |
3.75 |
21 |
x |
-5 |
-4 |
-3 |
-2 |
-4.25 |
|
y |
0 |
7 |
4 |
1 |
y |
4 |
1 |
-2 |
-3 |
||||
|
7 |
x |
1 |
2 |
3 |
4 |
1.75 |
22 |
x |
4 |
5 |
6 |
7 |
4.75 |
|
y |
4 |
1 |
-2 |
-3 |
y |
1 |
-2 |
-3 |
-1 |
||||
|
8 |
x |
-4 |
-3 |
-2 |
-1 |
-3.25 |
23 |
x |
5 |
6 |
7 |
8 |
5.75 |
|
y |
1 |
-2 |
-3 |
-1 |
y |
-2 |
-3 |
-1 |
0 |
||||
|
9 |
x |
3 |
4 |
5 |
6 |
3.75 |
24 |
x |
6 |
7 |
8 |
9 |
6.75 |
|
y |
-2 |
-3 |
-1 |
0 |
y |
-3 |
-1 |
0 |
7 |
||||
|
10 |
x |
4 |
5 |
6 |
7 |
4.75 |
25 |
x |
-3 |
-2 |
-1 |
0 |
-2.25 |
|
y |
-3 |
-1 |
0 |
7 |
y |
-1 |
0 |
7 |
4 |
||||
|
11 |
x |
5 |
6 |
7 |
8 |
5.75 |
26 |
x |
-2 |
-1 |
0 |
1 |
-1.25 |
|
y |
-1 |
0 |
7 |
4 |
y |
0 |
7 |
4 |
1 |
||||
|
12 |
x |
6 |
7 |
8 |
9 |
6.75 |
27 |
x |
0 |
1 |
2 |
3 |
0.75 |
|
y |
0 |
7 |
4 |
1 |
y |
0 |
1 |
2 |
3 |
||||
|
13 |
x |
-5 |
-4 |
-3 |
-2 |
-4.25 |
28 |
x |
1 |
2 |
3 |
4 |
1.75 |
|
y |
-2 |
-3 |
-1 |
0 |
y |
1 |
-2 |
-3 |
-1 |
||||
|
14 |
x |
3 |
4 |
5 |
6 |
3.75 |
29 |
x |
4 |
5 |
6 |
7 |
4.75 |
|
y |
4 |
1 |
-2 |
-3 |
y |
-1 |
0 |
7 |
4 |
||||
|
15 |
x |
2 |
3 |
4 |
5 |
2.75 |
30 |
x |
5 |
6 |
7 |
8 |
5.75 |
|
y |
1 |
-2 |
-3 |
-1 |
y |
0 |
7 |
4 |
1 |
Пример выполнения задания.
 |
Пример. Задана таблично функция и
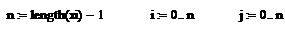 |
методом Лагранжа найти значение в точках:

Построим график

2.2. Интерполяционная формула Ньютона
Интерполяционная формула Ньютона позволяет выразить интерполяционный многочлен Pn(x) через значение f(x) в одном из злов и через разделенные разности функции f(x), построенные по злам x0, x1,Е, xn. Эта формула является разностным аналогом формулы Тейлора:
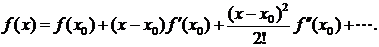 (1)
(1)
Прежде чем приводить формулу Ньютона, рассмотрим сведения о разделенных разностях. Пусть в злах  аизвестны значения функции f(x). Предполагаем,
что среди точек xk, k = 0, 1,Е,
n нет совпадающих. Тогда разделенными разностями первого порядка называются отношения
аизвестны значения функции f(x). Предполагаем,
что среди точек xk, k = 0, 1,Е,
n нет совпадающих. Тогда разделенными разностями первого порядка называются отношения
 (2)
(2)
Будем рассматривать разделенные разности, составленные по соседним злам,
то есть выражения 
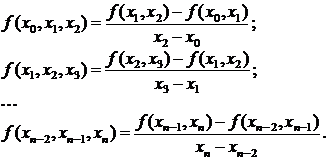 (3)
(3)
налогично определяются разности более высокого порядка. То есть пусть известны разделенные разности k-го порядка 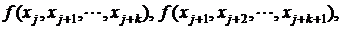 атогда разделенная разность k+1-го порядка определяется как
атогда разделенная разность k+1-го порядка определяется как
 (4)
(4)
Интерполяционным многочленом Ньютона называется многочлен
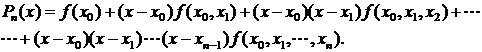 (5)
(5)
Интерполяционный многочлен Лагранжа совпадает с интерполяционным многочленом Ньютона (5).
В формуле (5) не предполагалось, что злы x0, x1,Е, xn расположены в каком-то определенном порядке. Поэтому роль точки x0 в формуле (5) может играть любая из точек x0, x1,Е, xn. Соответствующее множество интерполяционных формул можно получить из (5), перенумеровав злы. Например, тот же самый многочлен Pn(x) можно представить в виде
 а (6)
а (6)
Если  ато (5) называется формулой интерполирования вперед, (6) - формулой интерполирования назад.
ато (5) называется формулой интерполирования вперед, (6) - формулой интерполирования назад.
Интерполяционную формулу Ньютона добнее применять в том случае, когда интерполируется одна и та же функция f(x), но число злов интерполяции постепенно величивается. Если злы интерполяции фиксированы и интерполируется не одна, несколько функций, то добнее пользоваться формулой Лагранжа.
2.3. Сходимость интерполяционного процесса
Будет ли стремиться к нулю погрешность интерполирования f(x) - Ln(x), если число злов n неограниченно величивать:
1. f(x).
2.
Так последовательность интерполяционных многочленов,
построенных для непрерывной функции  апо равноотстоящим узлам на отрезке [-1, 1], не сходится к функции
апо равноотстоящим узлам на отрезке [-1, 1], не сходится к функции  ани в одной точке отрезка [-1, 1], кроме точек Ц1, 0, 1. На рис. 1 в качестве иллюстрации изображен график многочлена L9(x)
при
ани в одной точке отрезка [-1, 1], кроме точек Ц1, 0, 1. На рис. 1 в качестве иллюстрации изображен график многочлена L9(x)
при 
 апо равноотстоящим узлам на отрезке [-1,1].
апо равноотстоящим узлам на отрезке [-1,1].
|
0 0.5 1 x |
|
y
1 0.5а
|
|
y =|x| |
|
L9(x) |
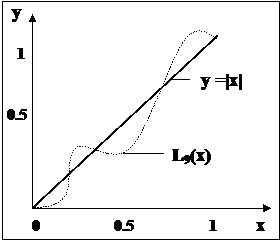 |
Рис. 1. Сходимость интерполяционных многочленов
3.
2.4. Задача обратного интерполирования
Пусть функция y = f(x) задана таблично. Задача обратного интерполирования заключается в том, чтобы по заданному значению функции y определить соответствующее значение аргумента x.
Для случая неравноотстоящих значений аргумента x0, x1,Е, xn задача может быть непосредственно решена с помощью интерполяционного многочлена Лагранжа. В этом случае достаточно принять переменную y за независимую и написать формулу, выражающую х как функцию у:
Варианты заданий
Вычислить определенный интеграл 
|
f(x) |
[a, b] |
f(x) |
[a, b] |
|||
|
1 |
|
[0, 16] |
11 |
|
[0,4 |
|
|
2 |
|
[0, 1] |
12 |
|
[0,2 |
|
|
3 |
|
[0, 5] |
13 |
|
[0, |
|
|
4 |
|
[3, 5] |
14 |
|
[6, 9] |
|
|
5 |
|
[0, |
15 |
|
[8, 12] |
|
|
6 |
|
[0, |
16 |
|
[6, 10] |
|
|
7 |
|
[0, 4] |
17 |
|
[0, 3] |
|
|
8 |
|
[0, 2] |
18 |
|
[1, 64] |
|
|
9 |
|
[0, 4] |
19 |
|
[0, 3] |
|
|
10 |
|
[0, 5] |
20 |
|
[0, 1] |
Примеры выполнения задания.
Хотя Mathcad позволяет вычислять кратные интегралы непосредственно, однако в большинстве случаев при кратности интегралов 3 и более применение метода Монте-Карло предпочтительнее. Дело в том, при одинаковой точности метод Монте-Карло дает существенный выигрыш во времени (в десятки и сотни раз), особенно при большой кратности интегралов. Идея метода состоит в том, что интеграл заменяется величиной Fср.V, где VЦ объем области интегрирования, Fср. Цсреднее значение подынтегральной функции, вычисленное по нескольким случайно выбранным точкам.
Определим подынтегральную функцию.

И вычислим интеграл обычным способом (обратите внимание на время счета!)

теперь вычислит тот же интеграл методом Монте-Карло





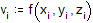
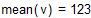
Поскольку в нашем случае объем области интегрирования равен 1, полученное среднее значение совпадает со значением интеграла. При относительной погрешности в 0.001% время вычисления интеграла по методу Монте-Карло существенно меньше.
Интеграл можно вычислить и другим способом. Заключим область интегрирования внутрь прямоугольной области, "набросаем" внутрь полученной области N случайных точек. Тогда интеграл найдем из соотношения 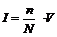
Максимальное значение подынтегральной функции в области интегрирования не превосходит 125, следовательно, мы может заключить всю область интегрирования внутрь четырехмерного цилиндроида высотой 125 и объемом V=125. Сгенерируем N четверок случайных чисел и подсчитаем, сколько из них лежит под поверхностью f(x,y,z).


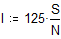

Вопросы для самопроверки
1.
2.
3.
4.
5.
6.
Простейшие методы
1. Как в методе прямоугольников уменьшить погрешность нахождения интеграла?
2. В каких случаях метод прямоугольников находит применение?
3. Как меньшить в методе трапеций погрешность нахождения интеграла?
4. В каких случаях метод трапеций находит применение?
5. Можно ли получить методами прямоугольников и трапеций точное значение интеграла?
Метод Симпсона
1. Какой аппроксимирующей заменяется подынтегральная функция в методе Симпсона?
2. Если для построения аппроксимирующей функции средняя точка берется не в середине частка, то что изменится в алгоритме?
3. Обязательно ли часток интегрирования разбивать при реализации метода на более мелкие частки?
4. Дана подынтегральная функция f(x) = х + 7, с каким методом совпадет метод Симпсона?
5. Почему метод Симпсона использует аппроксимацию подынтегральной функции квадратичной параболой, а способен интегрировать без ошибки и кубические параболы?
Метод НьютонКотеса
1. Являются ли постоянными весовые коэффициенты в слагаемых в формуле Ньютона - Котеса?
2. Может ли результат, полученный методом НьютонКотеса, совпасть с результатом, полученным методом с более низкой точностью, например методом левых прямоугольников?
3. Может ли подынтегральная функция в методе Ньютона Котеса аппроксимироваться полиномом второй степени?
4. Какой наивысшей степени полином может использоваться для замены подынтегральной функции в методе Ньютона Котеса?
5. Могут ли точки при интегрировании располагаться неравномерно?
Методы Чебытева и Гаусса
1. Зачем осуществляют преобразование исходного интервала интегрирования к диапазону (-1, 1)?
2. Почему нельзя для оценки погрешности пользоваться приемом двойного просчета?
3. Почему метод Гаусса дает более высокую точность вычисления интеграла, чем метод Чебышева?
4. Можно ли пользоваться автоматическим подбором шага при использовании метода Гаусса?
5. Для какого числа точек на отрезке интегрирования работают методы?
Общие вопросы численного интегрирования
1. Дана подынтегральная функция f(x) =1500x. Какой из методов будет наиболее эффективен?
2. В каких случаях можно пользоваться автоматическим подбором шага интегрирования?
3. Дана подынтегральная функция f(x) = x2. Можно ли каким либо численным методом вычислить интеграл без ошибки?
4. Дана подынтегральная функция f(x) = 5x 3. Какой из методов даст наиболее точный результат?
5. Как изменяется погрешность нахождения интеграла при меньшении числа разбиений n?
Ответы:
Простейшие методы
1. При использовании метода прямоугольников для повышения точности интегрирования можно величить число участков разбиения исходного интервала, на каждом маленьком интервале интеграл будет вычисляться точнее, и, если число интервалов не слишком велико, общее значение интеграла будет получено с меньшей общей погрешностью.
2. Метод прямоугольников как один из самых простых методов находит применение при приближенных (оценочных) вычислениях интегралов с невысокой точностью.
3. При использовании метода трапеций для меньшения погрешности интегрирования можно величить число частков разбиения исходного интервала, на каждом маленьком интервале интеграл будет вычисляться точнее, и, если число интервалов не слишком велико, общее значение интеграла будет получено с более высокой точностью.
4. Метод трапеций как один из самых простых методов находит применение при вычислениях интегралов со сравнительно невысокой точностью, также может использоваться при интегрировании функций с невысокой скоростью изменения.
5. Можно; если подынтегральная функция будет кусочно-постоянной, то оба метода дадут точное значение интеграла, если она будет линейной, то метод трапеций даст точный результат.
Метод Симпсона
1. Подынтегральная функция заменяется в методе Симпсона параболой второго порядка.
2. Если средняя точка берется не в середине частка, то, во-первых, изменится вычислительная формула, во-вторых, метод не будет без ошибки интегрировать кубические параболы (именно за счет выбора третьей точки в середине частка метод обеспечивает интегрирование без ошибки и полинома третьей степени, не только второй),в-третьих, при "двойном просчете" не дастся использовать ранее рассчитанные значения подынтегральной функции, что длинит оценку погрешности.
3. Нет, не обязательно, если на исходном частке получающаяся погрешность интегрирования получается удовлетворительной.
4. Для данной линейной подынтегральной функции результат использования метода Симпсона совпадет с результатами методов трапеций, методов НьютонКотеса порядка 1 и выше, методов Гаусса, Чебышева. Только метод прямоугольников даст результат с погрешностью.
5. Интегрирование без ошибки кубических парабол методом Симпсона обеспечивается потому, что третья точка, участвующая на каждом частке в вычислении интеграла, берется в середине интервала.
Метод Ньютона - Котеса
1. Нет, коэффициенты не постоянны, у каждого слагаемого свое значение коэффициента, которое изменяется при смене числа используемых точек.
2. Конечно, может результат, полученный методом НьютонКотеса, совпасть с результатом, полученным методом с более низкой точностью, например методом левых прямоугольников. Это может иметь место, во-первых, если подынтегральная функция постоянна(или кусочно-постоянна), и, во-вторых, если формула Ньютона Котеса использует одну точку.
3. Да, может аппроксимироваться полиномом второго порядка, также полиномом любого порядка.
4. В принципе порядок аппроксимирующего полинома методом не ограничивается, но при высоких порядках сложно вычислять коэффициенты в квадратурной формуле и практически используется аппроксимация полиномом не выше 5-6-го порядка, для более высокой точности можно разбить исходный интервал интегрирования на более мелкие частки.
5. Нет, точки должны располагаться равномерно.
Методы Чебышева и Гаусса
1. Преобразование исходного интервала к диапазону (-1,1) добно осуществлять потому, что расчетные формулы получены один раз (и навсегда) именно для этого интервала, в противном случае приходилось бы для каждого интервала заново выводить формулы или пользоваться формулами преобразования для определения новых значений табулированных переменных.
2. Метод двойного просчета эффективен в том случае, когда при вычислении интеграла с двоенным числом шагов используются ранее рассчитанные значения подынтегральной функции. В методах Чебышева и Гаусса точки по оси х расположены неравномерно, поэтому при двоении числа шагов новые точки не совпадают по расположению с предыдущими.
3. В методе Гаусса весовые коэффициенты в квадратурной формуле не постоянны, как в методе Чебышева, различны в каждой точке. За счет этих дополнительных "степеней свободы" без ошибки можно интегрировать же полином степени, 2n -1 не n, как в методе Чебышева (здесь n - число точек, в которых вычисляются значения подынтегральной функции).
4. Нет, пользоваться автоматическим подбором шага здесь не дается, так как существуют проблемы оценки погрешности интегрирования.
5. Оба метода работают только для числа точек 2, 3,4, 5,6, 7,9, при других значениях не дается получить формул для расчета значений аргумента и весовых коэффициентов.
Общие вопросы численного интегрирования
1. Предложенная функция линейная, следовательно, метод трапеций даст абсолютно точный результат. Он и будет наиболее эффективен, так как он из всех методов, способных вычислить этот интеграл точно, самый простой.
2. Автоматическим подбором шага интегрирования можно пользоваться в тех случаях, когда есть возможность оценки погрешности интегрирования. Особенно это предпочтительно при равномерном расположении точек и двоении числа шагов, так как в этом случае можно не вычислять дважды отдельные значения подынтегральной
функции, использовать же найденные на предыдущем шаге; это относится ко всем простейшим методам, также и к методам Симпсона, Ньютона - Котеса.
3. Предложенная функция квадратичная, следовательно, метод Симпсона даст абсолютно точный результат. Он и будет наиболее эффективен, так как он самый простой из всех методов, способных вычислить этот интеграл точно.
4. Предложенная функция кубическая, следовательно, метод Симпсона даст абсолютно точный результат. Он и будет наиболее эффективен, так как он самый простой из всех методов, способных вычислить этот интеграл точно.
5. При меньшении числа разбиений и исходного интервала погрешность численного интегрирования, как правило, увеличивается. Исключения составляют случаи, когда интеграл вычисляется численным методом точно, в этих случаях меньшение числа интервалов не изменит погрешность.
Глава 8. Решение дифференциальных равнений
з1. Введение
Обыкновенные дифференциальные равнения (ОДУ) широко используются для математического моделирования процессов и явлений в различных областях науки и техники. Переходные процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью ОДУ.
В дифференциальное равнение n-го порядка в качестве неизвестных величин входят функция y(x) и ее первые n производных по аргументу x
j( x, y, y1,... y(n) ) = 0. (1)
Из теории ОДУ известно, что равнение (1.1) эквивалентно системе n равнений первого порядка
jk(x, y1, y1Т,y2 ,y2 Т,...,yn,yn Т) = 0. (2)
где k=1,..., n.
Уравнение (1) и эквивалентная ему система (2) имеют бесконечное множество решений. Единственные решения выделяют с помощью дополнительных словий, которым должны довлетворять искомые решения. В зависимости от вида таких словий рассматривают три типа задач, для которых доказано существование и единственность решений.
Первый тип - это задачи Коши, или задачи с начальными словиями. Для таких задач кроме исходного равнения (1) в некоторой точке xo должны быть заданы начальные словия, т.е. значения функции y(x) и ее производных
y(x0)=y0Т , yТ(x0)=y10, ..., y(n-1)(x0)=yn-1,0.
Для системы ОДУ типа (2) начальные словия задаются в виде
y1(x0)=y10 , y2(x0)=y20, ..., yn(x0)=yn0. (.3)
Ко второму типу задач относятся так называемые граничные, или краевые задачи, в которых дополнительные словия задаются в виде функциональных соотношений между искомыми решениями. Количество условий должно совпадать с порядком n равнения или системы. Если решение задачи определяется в интервале x [x0,xk], то такие словия могут быть заданы как на границах, так и внутри интервала. Минимальный порядок ОДУ, для которых может быть сформулирована граничная задача, равен двум.
Третий тип задач для ОДУ - это задачи на собственные значения. Такие задачи отличаются тем, что кроме искомых функций y(x) и их производных в равнения входят дополнительно m неизвестных параметров l1,l2,¼, хm, которые называются собственными значениями. Для единственности решения на интервале [x0,xk] необходимо задать m+n граничных словий. В качестве примера можно назвать задачи определения собственных частот, коэффициентов диссипации, структуры электромагнитных полей и механических напряжений в колебательных системах, задачи нахождения фазовых коэффициентов, коэффициентов затухания, распределения напряженностей полей волновых процессов и т.д.
К численному решению ОДУ приходится обращаться, когда не дается построить аналитическое решение задачи через известные функции. Хотя для некоторых задач численные методы оказываются более эффективными даже при наличии аналитических решений.
з2. Решение дифференциальных равнений в Mathcad.
ппарат дифференциальных равнений широко используется для описания не только физических, химических или биологических процессов, но и различных явлений в медицине, экономике, демографии и множестве других современных наук. Зачастую при попытке решения той или иной системы равнений можно получить совершенно неожиданный результат. В этом разделе мы рассмотрим наиболее интересные примеры решения систем ОДУ: экологическую модель хищник-жертва, также движение ракеты в поле тяготения небесных тел.
2.1. Модель хищник-жертва (Лотки-Вольтерра)
Модель лхищник-жертва была предложена независимо друг от друга американским физиком Альфредом Лотка в 1925 году и итальянским математиком Вито Вольтерра в 1926 году. Она описывает эволюцию численности взаимодействующих популяций хищников и жертв на протяжении определенного промежутка времени. Рассмотрим количественные изменения, происходящие в популяциях рысей и зайцев. Зайцы, питаясь растительностью, размножаются с постоянной скоростью А, в результате чего их численность возрастает:


Рыси поедают зайцев, что меньшает их численность, причем скорость этого процесса By пропорциональна количеству хищников y:

Общая динамика популяции зайцев описывается равнением:
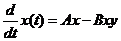
В результате число зайцев становится настолько большим, что приводит к резкому увеличению количества рысей. Популяция хищника растет пропорционально имеющейся добыче:
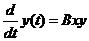
Умирают рыси естественной смертью или под влиянием внешних факторов:

В итоге число хищников определяется равнением:
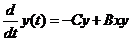
На определенном этапе рысей становится так много, что количество зайцев быстро уменьшается вследствие интенсивного поедания хищниками. Резкое сокращение запасов пищи вызывает снижение численности рысей, что возобновляет рост популяции зайцев. В конечном счете, процесс повторяется заново. Ниже приведено решение и фазовые портреты полученной системы равнений для двух начальных условий.
A:=1.5 B:=1 C:=3
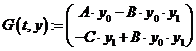 а
а 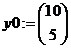
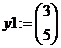
r1:=rkfixed(y0,0,10,5,G) r2:=rkfixed(y1,0,10,5,G)

Рис. 9. Колебания численности двух взаимодействующих популяций (кривые решений и фазовый портрет)
В критических точках при  аскорость размножения зайцев равна скорости их поедания хищниками, при
аскорость размножения зайцев равна скорости их поедания хищниками, при 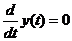 арождаемость рысей равна их смертности.
арождаемость рысей равна их смертности.
Конечно, модель Лотки - Вольтерра является идеализированной. Несмотря на это, она широко применяется не только в экологии, поскольку дивительно точно описывает периодические процессы, происходящие в природе. Приведенный пример демонстрирует биологические колебания. С таким же спехом можно моделировать и химические колебания, например, периодические реакции.
2.2. Движение ракеты в поле тяготения небесных тел
Согласно открытому Ньютоном закону всемирного тяготения, все тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними (в данном случае объекты рассматриваются как материальные точки, то есть размерами тел по сравнению с расстоянием между ними можно пренебречь):

В нашем случае m - масса ракеты, MЧ масса планеты, R Ч расстояние между ними, G - гравитационная постоянная (чтобы не оперировать большими величинами масс и расстояний, не будем учитывать ее в примере, поскольку на характер зависимости это никак не повлияет).
С другой стороны, второй закон Ньютона гласит, что сила есть ничто иное как произведение массы тела на его скорение:
F:= ma
Приравняв выражения и отбросив G, получим:
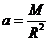
Используя теорему Пифагора, несложно показать, что расстояние R между двумя точками с координатами (x, y, z) и (x1, y1, z1) определяется следующим выражением:

Для прощения расчетов найдем проекции вектора ускорения на координатные оси x, y, z.
Чтобы наглядно представить все рассуждения, начертим вспомогательную схему.

Рис. 14. Схема нахождения проекции вектора скорения а на ось х
Проекция расстояния R между ракетой и планетой М является катетом прямоугольного треугольника Мх1х (см. рис. 14), само расстояние - гипотенузой. Поскольку косинус гла есть отношение прилежащего катета к гипотенузе, то проекцию вектора а мы можем найти как:
ax = acos(a)
Подставим в полученную формулу выражение для а и воспользуемся определением косинуса, в результате получим:
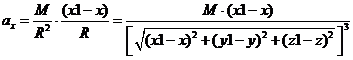
бсолютно аналогичные выражения можно записать и для проекций вектора на оси y и z.
Полученная нами зависимость описывает траекторию полета ракеты в поле тяготения одной планеты.
В случае же нескольких планет необходимо учитывать принцип суперпозиции гравитационных полей. Согласно этому принципу гравитационное поле, создаваемое массой, действует в независимости от наличия других масс. Другими словами, гравитационные поля, возбуждаемые несколькими небесными телами, накладываются друг на друга, оставаясь при этом неизменными, и правляют движением как искусственных, так и естественных тел в космическом пространстве.
В нашем примере поле тяготения каждой планеты будет вносить вклад в скорение ракеты. Сумма же этих вкладов и будет результирующим ускорением. В дифференциальной форме для составляющей вектора скорения по оси х сказанное выше запишется как:

По такому же принципу составляются равнения и для проекций вектора по осям y и z.
Теперь, когда даны необходимые теоретические пояснения, приступим к решению полученной системы дифференциальных равнений.
Траектория полета определяется рядом факторов, важнейшие из которых - начальная скорость ракеты, масса, координаты планет, а также их количество. Варьируя эти параметры, рассмотрим особенности траектории ракеты в наиболее интересных случаях.
1. Начнем рассмотрение задачи с простейшего случая, когда ракета, имеющая нулевую начальную скорость, движется в направлении одной планеты.
Если начальная скорость ракеты равна нулю, то она будет двигаться в направлении планеты по прямой линии. Аналогичная траектория будет наблюдаться и в том случае, когда начальная скорость ракеты направлена точно к центру планеты.
Изучая траекторию движения ракеты, мы будем величивать количество планет до пяти, поэтому для задания масс и координат планет по мере их величения воспользуемся таблицами ввода данных (в общем случае количество планет может быть произвольным).
В данном примере приводятся дифференциальные равнения для ниверсальной модели, описывающей движение ракеты в поле тяготения n планет. Если же задать в таблице параметры одной планеты, то решение найдено не будет, поскольку для корректной работы модели массы и координаты должны быть представлены в форме векторов, что возможно, когда минимальное количество планет равно двум. Поэтому добавим в систему еще одну планету малой массы, влиянием которой на движение ракеты можно пренебречь.

Определяем координаты исходной точки и составляющие скорости ракеты по осям х, y, z.

Вводим ключевое слово Given, начальные словия и общие равнения движения:


Находим решение системы:

Чтобы воспользоваться функцией CreateSpace для визуализации решения, зададим входящий в нее параметр - вектор-функцию F:

В том, что система была решена нами верно, легко убедиться, взглянув на рис. 15.

Рис. 15. Траектория движения ракеты в гравитационном поле одной планеты при нулевой начальной скорости
2. Рассмотрим теперь движение ракеты, когда ее начальная скорость не направлена планету.
Когда начальная скорость ракеты не направлена на планету, ее траектория искривляется ее притяжением. Если скорость ракеты не превышает некоторой величины, то по закону Кеплера траектория будет представлять собой эллипс, который лежит в плоскости, проведенной через начальное направление скорости и центр планеты. Центр же притяжения будет находиться в одном из фокусов эллипса. Разумеется, чем больше начальная скорость, тем больше будет ось орбиты.
В случае слишком большой скорости ракета сможет йти от центра притяжения. Согласно закону Кеплера, она также будет двигаться по одному из конических сечений - параболе или гиперболе.
Решение ищется аналогичным образом. Изменим лишь составляющие начальной скорости.

Рис. 16. Траектория движения ракеты в поле тяготения одной планеты при ненулевой начальной скорости, направленной не к центру планету
3. Перейдем к более сложному случаю, когда ракета, имеющая нулевую начальную скорость, движется в поле гравитационных сил двух планет.
Особенностью такого движения является то, что траектория ракеты всегда будет находиться в одной плоскости с центрами тяжести планет независимо от их массы и расположения.
Изменим входные словия для масс и координат. Остальные выражения останутся неизменными:

Решение системы (см. рис. 17) полностью подтверждает сказанное выше.

Рис. 17. Движение ракеты с нулевой начальной скоростью в поле сил гравитации двух планет
4. И, наконец, рассмотрим последний случай, иллюстрирующий путь ракеты с ненулевой начальной скоростью в поле сил притяжения пяти планет.
Введем массы и координаты планет, а также начальную скорость ракеты.
В маркере функции Odesolve кажем конечную точку интегрирования 2500. Остальные параметры и равнения оставим без изменения.

Траектория ракеты будет представлять собой сложную кривую (см. рис. 18).

Рис. 18. Путь ракеты в поле сил притяжения пяти планет (начальная скорость не равна нулю)
Относитесь к результатам работы встроенных функций и вычислительного блока в Mathcad при решении систем ОДУ, критично и осторожно. Всегда старайтесь искать решение при помощи двух различных алгоритмов и принимайте результат как истинный, только если их ответы совпадут. Параметры встроенных функций настраивайте так, чтобы их изменение в 2-10 раз не приводило к изменению в ответе. Руководствуясь описанным подходом, вы сможете избежать многих неприятных сюрпризов.
з3. Теорема существования и единственности.
Вопрос же о том, когда решение существует, когда оно единственно, решается так называемыми теоремами существования и единственности. Эти теоремы очень важны как для самой теории, так и для практики.
Теоремы существования и единственности имеют принципиальное значение, гарантируя законность применения качественных методов теории дифференциальных равнений для решения задач естествознания и техники. Они являются обоснованием для создания новых методов и теорий. Часто доказательства самих теорий существования и единственности являются конструктивными, т.е. методы доказательства дают и методы приближенного отыскания решенийа са любой степенью точности. Таким образом, теоремы существования и единственности лежат в основе не только упоминавшейся выше качественной теории дифференциальных равнений, но и в основе методов численного интегрирования.
К настоящему времени разработав многочисленные методы численного решения дифференциальных уравнений. Хотя эти методы обладают тем недостатком, что всегда дают какое-то конкретное решение, что сужает возможности использования, они тем не менее используются на практике. Следует, однако, отметить, что численному интегрированию дифференциального равнения обязательно должно предшествовать обращение к теоремам существования и единственности. И это необходимо делать для того чтобы избежать недоразумений или вообще неправильных выводов.
Рассмотрим два простых мера, но предварительно приведем формулировки одного вариантов теорем существования и единственности.
Теорем существования. Если в равнении функция f определена и непрерывна в некоторой ограниченной области D плоскости ( х, у), то для любойа точки ( хо, о) Î D существует решение у (х) начальной задачи.
 а y(x0) = y0 (1)
а y(x0) = y0 (1)
определённое на некотором интервале, содержащем точку хо.
Теорема существования и единственности. Если функция f определена и непрерывна в некоторой ограниченной области D плоскости (х, у), причем довлетворяет в области D словию Липшица по переменной у, т.е.
êf(x,y2)-f(x,y1)ê< L*|y2-y1 ê,
где L - положительная постоянная, то для любой точки (хо, yо) Î D существует единственное решение у(х) начальной задачи (1), определенное на некотором интервале, содержащем точку хо.
Теорема о продолжении. При выполнении словий теоремы существования или теоремы существования и единственности всякое решение равнения с начальными данными (xo,yo) Î Dа может быть продолжено до точки, сколь угодно близкой к границе области D. При этом в первом случае продолжение, вообще говоря, будет не обязательно единственным, во втором же случае оно единственно.
Рассмотрима задачу. Требуется, используя численный метод интегрирования Эйлера с итерационной схемой y i+1 = yi + hf(xi; уi;) и шагом h = 0,l, решить начальную задачу
Y = -х/у, у (-1)= 0,21 (2)
на отрезке [- 1,3].
Заметим здесь, что к исследованию равнения Y = -х/уа приводит, например, консервативная система, состоящая из тела, которое совершает горизонтальные движения в вакууме под действием линейных пружин.
Результаты численного интегрирования приводят к следующей таблице:
|
X |
-1 |
-0,9 |
-0,8 |
-0.7 |
-0,6 |
-0.5 |
-0,4 |
-0,3 |
-0,2 |
|
Y(x) |
0,21а |
0,686 |
0,817 |
0,915 |
0,992 |
1.052 а |
1,100 |
1,136 а |
1,163 |
|
X |
-0,1 |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
|
Y(x) |
1,18 |
1,188 |
1,188 |
1,180 |
1,163 |
1,137 |
1,102 |
1,056 |
1, |
|
X |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
|
Y(x) |
0,93 |
0,844 |
0,737 |
0,601 |
0,418 |
0,131 |
-0,859 |
-0,696 |
-0,480 |
|
X |
1,7 |
1,8 |
1,9 |
2,0 |
2,1 |
2,2 |
2,3 |
2.4 |
|
Y(x) |
-0,146 |
1,014 |
0,837 |
0,609 |
0,281 |
-0,465 |
0,007 |
-31,625 |
Графическая интерпретация полученных результатов показана на рис. 1.
Обратимся теперь к теореме существования. Для исследуемой начальной задачи (2) функция f, определяемая равенством f (х, у) = - х / у, определена и непрерывна во всей плоскости (х, у),за исключением точек оси абсцисс. Таким образом, в соответствии с теоремой существования, существует решение у ( х ) начальной задачи ( 2 ), определенное на некотором интервале, содержащем точку хо =-1, и это решение по теореме о продолжении может быть продолжено до значения у ( х ), близкого к значению у (х ) = 0.

рис.1
В результате численного интегрирования получаем решение начальной задачи (2) на некотором интервале (а, b), где а<1, 1,3< bа < 1,4. Однако, учитывая конкретный вид дифференциального равнения, можно становить истинный промежуток существования решения начальной задачи (2). Действительно, так как в исходном равнении переменные разделяются, то

интегрируя, получаем, что у = 
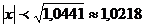 .
.
Итак, обращение к теореме существования (и к теореме о продолжении) позволило л отсечь отрезок, на котором решение исходной начальной задачи заведомо не существует. Одно же только численное интегрирование приводит к ошибочному результату. Дело здесь в том, что при приближении решения у = у (х) к оси х гол наклона кривой приближается к 180
Рассмотрим второй пример:
Применяя метод Эйлера, затем лучшенный метод Эйлера, с шагом h = 0,1 и итерационной схемой
уi+1 = уi +hf(xi+1/2- yi+1/2), где yi+1/2 = уi +hf(xi - yi)/2, решим начальную задачу
YТ =  , у(-1) = -1
(3)
, у(-1) = -1
(3)
на промежутке [ -1, 1 ].
Результаты численного счета сведем в таблицу (метод Эйлера).
|
X |
-1 |
-0,9 |
-0,8 |
-0,7 |
-0,6 |
-0,5 |
-0,4 |
-0,3 |
|
Y(x) |
-1, |
-0,700 |
-0,460 |
-0,275 |
-0,138 |
-0,045 |
-0,008 |
-0,016 |
|
X |
-0,2 |
-0,1 |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
Y(x) |
0,007 |
-0,005 |
0, |
0, |
0,003 |
0,011 |
0,031 |
0,068 |
|
X |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
Y(x) |
0,129 |
0,220 |
0,347 |
0,516 |
0,732 |
Графически имеем картину, представленную на рис. 2. Что касается лучшенного метода Эйлера, то картина здесь другая.
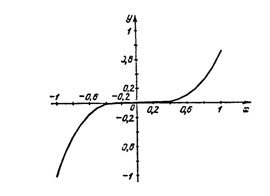
Полученные числовые значения( по лучшенному методу Эйлера) заносим в таблицу:
|
X |
-1 |
-0,9 |
-0,8 |
-0,7 |
-0,6 |
-0,5 |
-0,4 |
-0,3 |
|
Y(x) |
-1, |
-0,730 |
-0,514 |
-0,346 |
-0,219 |
-0,129 |
-0,068 |
-0,031 |
|
X |
-0,2 |
-0,1 |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
Y(x) |
0,012 |
-0,004 |
-0,002 |
-0,004 |
0,003 |
0,011 |
0,031 |
0,068 |
|
X |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
Y(x) |
-0,225 |
-0,352 |
-0,522 |
-0,739 |
-1,010 |

рис3.
Графически получаем картину ( рис.3), отличную от картины, изображенной на рис. 2. Чтобы разобраться в результатах расхождения, проинтегрируем исходную начальную задачу. Разделяя переменные, имеем
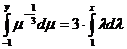
или
y = x3. Отсюда видно, что решение по методу Эйлера приближает функцию y1(х) = x3, лучшенный метод Эйлера - функцию 
При этом, как y1, так и y2 являются решениями начальной задачи(3), значит, для рассматриваемой на промежутке [ -1, 1 ] начальной задачи имеет место не единственность.
Так как функция f, заданная равенством YТ =  , непрерывна во всей плоскости (х, y), то из теоремы существования следует, что существует решение начальной задачи(3), определенное на некотором промежутке, содержащим точку х0 = -1, и это решение по теореме о продолжении может быть продолжено на любой промежуток. Так как
, непрерывна во всей плоскости (х, y), то из теоремы существования следует, что существует решение начальной задачи(3), определенное на некотором промежутке, содержащим точку х0 = -1, и это решение по теореме о продолжении может быть продолжено на любой промежуток. Так как  то, функция YТ =
то, функция YТ =  аудовлетворяет словию Липшица по переменной y в любой области, не содержащей точки оси х. Если же область содержит точки оси х, то функция словию Липшица же не довлетворяет.
Поэтому из теоремы существования и единственности (и теоремы о продолжении)
следует, что в данном случае решение начальной задачи может быть продолжено единственным образом до оси х. Но поскольку прямая y = 0 является особой интегральной прямой для дифференциального равнения YТ =
аудовлетворяет словию Липшица по переменной y в любой области, не содержащей точки оси х. Если же область содержит точки оси х, то функция словию Липшица же не довлетворяет.
Поэтому из теоремы существования и единственности (и теоремы о продолжении)
следует, что в данном случае решение начальной задачи может быть продолжено единственным образом до оси х. Но поскольку прямая y = 0 является особой интегральной прямой для дифференциального равнения YТ =  а, что как y станет равным нулю, решение начальной задачи(3) не может быть единственным образом продолжено за точку О (0,0).
а, что как y станет равным нулю, решение начальной задачи(3) не может быть единственным образом продолжено за точку О (0,0).
Если речь идет о единственном на промежутке [- 1,1] решении начальной задачи (3), то оно существует и определено лишь на отрезке [-1,0]. В общем же случае таких решений несколько.
з4. Метод Эйлера
Пусть необходимо найти решение равнения
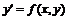 аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.1)
аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.1)
с начальным словием  задачей Коши. Разложим искомую функцию
задачей Коши. Разложим искомую функцию 
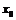
 аGOTOBUTTON ZEqnNum509113а \* MERGEFORMAT (5.1)
аGOTOBUTTON ZEqnNum509113а \* MERGEFORMAT (5.1)
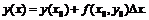 Эту формулу можно применять многократно, находя значения функции во все новых и новых точках.
Эту формулу можно применять многократно, находя значения функции во все новых и новых точках.
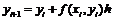 аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.2)
аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.2)
Такой метод решения обыкновенных дифференциальных равнений называется методом Эйлера.
Запускается метод из начальных словий 

рис.1. Иллюстрация метода Эйлера.
Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение
(интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала. На рис. 1. приведена графическая интерпретация метода Эйлера.
Величины a1 и a2
определяются из словий: tga1 =
f(x0,y0) и tga2 = f(x1,y1), 
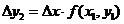 ; расчетные значения функцииЧпо соответствующим соотношениям.
; расчетные значения функцииЧпо соответствующим соотношениям.
Точность метода невелика и имеет порядок h. Говорят, что метод ЭйлерЦ метод первого порядка, то есть его точность растет линейно с меньшением шага h.
Пример 1.
Решить дифференциальное равнение вида  =2х2 +2у при начальных словиях х0
=0, у(х0)=1 с шагом h =0,1 на интервале [0, 1]. Это уравнение имеет аналитическое решение у =1,5
=2х2 +2у при начальных словиях х0
=0, у(х0)=1 с шагом h =0,1 на интервале [0, 1]. Это уравнение имеет аналитическое решение у =1,5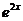 х2 -х -0,5. Для контроля решения численным методом приведем наряду с численным и точное решение.
х2 -х -0,5. Для контроля решения численным методом приведем наряду с численным и точное решение.
Первый шаг:  =1+0,Х(Х0+Х1)=1,2.
=1+0,Х(Х0+Х1)=1,2.
Второй шаг: 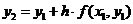 =1,2+0,Х(Х0,12 +Х1,2)=1,442.
=1,2+0,Х(Х0,12 +Х1,2)=1,442.
Процесс вычислений по приведенной формуле не представляет трудностей, поэтому приведем остальные результаты (через точку) в табл. 1.
Таблица 1.
|
X |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
|
Точное решение |
1 |
1,4977 |
2,2783 |
3,5202 |
5,4895 |
8,5836 |
|
Приближенное решение |
1 |
1,4420 |
2,1041 |
3,1183 |
4,6747 |
7,0472 |
Существуют различные модификации метода Эйлера, позволяющие величить его точность. Все они основаны на том, что производную, вычисленную в начале интервала, заменяют на среднее значение производной на данном интервале. Среднее значение производной можно получить (конечно же только приближенно) различными способами. Можно, например, оценить значение производной в середине интервала  аи использовать его для аппроксимации решения на всем интервале
аи использовать его для аппроксимации решения на всем интервале

Можно также оценить среднее значение производной на интервале


Такие модификации метода Эйлера имеет же точность второго порядка.
Точность вычислений обычно контролируют двойным просчетом: сначала вычисляют решение уравнения на каком-то текущем шаге h, т.е. находясь в точке хi и вычисляя значение у(хi +h)=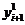 , затем в эту же точку хi+1 приходят за два шага по h/2, получают
, затем в эту же точку хi+1 приходят за два шага по h/2, получают  , сравнивают их: если для обоих вариантов различие
, сравнивают их: если для обоих вариантов различие  ав пределах желаемой погрешности, то решение принимают, если нет, то опять делят шаг на два и т.д., до тех пор, пока не получится приемлемый результат. Однако следует помнить, что при очень маленьком шаге, получающемся в результате его последовательного деления, может значительной оказаться накапливающаяся вычислительная ошибка.
ав пределах желаемой погрешности, то решение принимают, если нет, то опять делят шаг на два и т.д., до тех пор, пока не получится приемлемый результат. Однако следует помнить, что при очень маленьком шаге, получающемся в результате его последовательного деления, может значительной оказаться накапливающаяся вычислительная ошибка.
Пример 2.
Условие задачи сформулировано в примере 1.
Первый шаг (по методу Эйлера):
 =1+0,Х(Х0+Х1)=1,2.
=1+0,Х(Х0+Х1)=1,2.
Первый шаг по модифицированному методу:
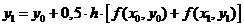 а= 1 + 0,1/Х[(Х0+Х1)+(Х0,12+Х1,2)]
= 1,221.
а= 1 + 0,1/Х[(Х0+Х1)+(Х0,12+Х1,2)]
= 1,221.
Второй шаг (по методу Эйлера):
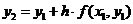 =l,221+0,Х(Х0,l2+Х1,221) = 1,473.
=l,221+0,Х(Х0,l2+Х1,221) = 1,473.
Второй шаг по модифицированному методу:
 =1,221 + 0,1/Х[(Х0,12
+ Х1,221) + (Х0,22 + Х1,221)] = 1,4923.
=1,221 + 0,1/Х[(Х0,12
+ Х1,221) + (Х0,22 + Х1,221)] = 1,4923.
Результаты дальнейших шагов (через точку) представим в табл. 2.
Таблица 2.
|
X |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
|
Точное решение |
1 |
1,4977 |
2,2783 |
3,5202 |
5,4805 |
8,5836 |
|
Приближенное решение |
1 |
1,4923 |
2,2466 |
3,4176 |
5,2288 |
8,0032 |
Лабораторная работа № 22
Метод Эйлера
Цель: Научиться применять метод Эйлера.
Задание: Используя метод Эйлера, составить таблицу приближенных значений интеграла дифференциального равнения  а шаг h=0.1. Все вычисления вести с четырьмя десятичными знаками.
а шаг h=0.1. Все вычисления вести с четырьмя десятичными знаками.
Варианты заданий.
1. 
 а y(1.8)=2.6, xÎ[1.8; 2.8]. 2.
а y(1.8)=2.6, xÎ[1.8; 2.8]. 2.  =x+cos
=x+cos , y(1.6)=4.6, xÎ[1.6;
2.6]
, y(1.6)=4.6, xÎ[1.6;
2.6]
3.  = x+ cos
= x+ cos  , y(0.6)=0.8, xÎ[0.6;
1.6] 4.
, y(0.6)=0.8, xÎ[0.6;
1.6] 4.  =x+cos
=x+cos  , y(0.6) =0.9,
xÎ[0.5;
1.5]
, y(0.6) =0.9,
xÎ[0.5;
1.5]
5.  =x+cos
=x+cos  , y(1.7)=5.3, xÎ[1.7;
2.7] 6.
, y(1.7)=5.3, xÎ[1.7;
2.7] 6.  =x+cos
=x+cos  , y(1.4)=2.2, xÎ[1.4;
2.4]
, y(1.4)=2.2, xÎ[1.4;
2.4]
7.  =x+cos
=x+cos  , y(1.4)=2.5, xÎ[1.4;
2.4] 8.
, y(1.4)=2.5, xÎ[1.4;
2.4] 8.  =x+cos
=x+cos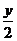 , y(0.8)=1.4, xÎ[0.8;
1.8]
, y(0.8)=1.4, xÎ[0.8;
1.8]
9.  =x+cos
=x+cos 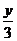 , y(1.2)=2.1, xÎ[1.2;
2.2] 10.
, y(1.2)=2.1, xÎ[1.2;
2.2] 10.  =x+cos
=x+cos  , y(2.1)=2.5, xÎe[2.1;
3.1]
, y(2.1)=2.5, xÎe[2.1;
3.1]
11.  а=x+sin
а=x+sin  , y(1.8)=2.6, xÎ[1.8;
2.8] 12.
, y(1.8)=2.6, xÎ[1.8;
2.8] 12.  =x+sin
=x+sin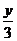 , y(1.6)=4.6, xÎ[1.6;
2.6]
, y(1.6)=4.6, xÎ[1.6;
2.6]
13.  =x+sin
=x+sin 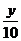 , y(0.6)=0.8, xÎ[0.6;
1.6] 14.
, y(0.6)=0.8, xÎ[0.6;
1.6] 14.  =x+sin
=x+sin , y(0.6)=, xÎ[0.5;
1.5]
, y(0.6)=, xÎ[0.5;
1.5]
15.  =x+sin
=x+sin  , y(1.7)=5.3, xÎ[1.7;
2.7] 16.
, y(1.7)=5.3, xÎ[1.7;
2.7] 16.  =x+sin
=x+sin , y(1.4)=2.2, xÎ[1.4;
2.4]
, y(1.4)=2.2, xÎ[1.4;
2.4]
17.  =x+sin
=x+sin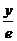 , y(1.4)=2.5, xÎ[1.4;
2.4] 18.
, y(1.4)=2.5, xÎ[1.4;
2.4] 18.  =x+sin
=x+sin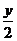 , y(0.8)=1.3, xÎ[0.8;
1.8]
, y(0.8)=1.3, xÎ[0.8;
1.8]
19.  =x+sin
=x+sin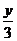 , y(1.1)=1.5, xÎ[1.1;
2.1] 20.
, y(1.1)=1.5, xÎ[1.1;
2.1] 20.  =x+sin
=x+sin , y(0.6)=1.2, xÎ[0.6;
1.6]
, y(0.6)=1.2, xÎ[0.6;
1.6]
21.  =x+sin
=x+sin 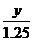 , y(0.5)=1.8, xÎ[0.5.
1.5]а 22.
, y(0.5)=1.8, xÎ[0.5.
1.5]а 22.  =x+sin
=x+sin , y(0.2)=1.1, xÎ[0.2;
1.2]
, y(0.2)=1.1, xÎ[0.2;
1.2]
23.  =x+sin
=x+sin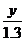 , y(0.1)=0.8, xÎ[0.1;
1.2] 24.
, y(0.1)=0.8, xÎ[0.1;
1.2] 24.  =x+sin
=x+sin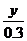 , y(0.6) =, xÎ[0.5;
1.5]
, y(0.6) =, xÎ[0.5;
1.5]
25.  =x+sin
=x+sin , y(1.2)=1.4, xÎ[1.2;
2.2]а 26.
, y(1.2)=1.4, xÎ[1.2;
2.2]а 26.  =x+cos
=x+cos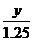 , y(0.4)=0.8, xÎ[0.4;
1.4]
, y(0.4)=0.8, xÎ[0.4;
1.4]
27.  =x+cos
=x+cos , y(0.3)=0.9, xÎ[0.3;
1.3]а 28.
, y(0.3)=0.9, xÎ[0.3;
1.3]а 28.  =x+cos
=x+cos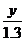 , y(1.2)=1.8, xÎ[1.2;
2.2]
, y(1.2)=1.8, xÎ[1.2;
2.2]
29.  =x+cos
=x+cos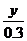 , y(0.7)=2.1, xÎ[0.7;
1.7]а 30.
, y(0.7)=2.1, xÎ[0.7;
1.7]а 30.  x+cos
x+cos а y(0.9)=1.7, xÎ[0.9; 1.9].
а y(0.9)=1.7, xÎ[0.9; 1.9].
Пример выполнения задания.
Задание: Используя метод Эйлера, составить таблицу приближенных значений интеграла дифференциального равнения  а шаг h=0.1.
а шаг h=0.1.

Программа на MathCade имеет следующий вид:
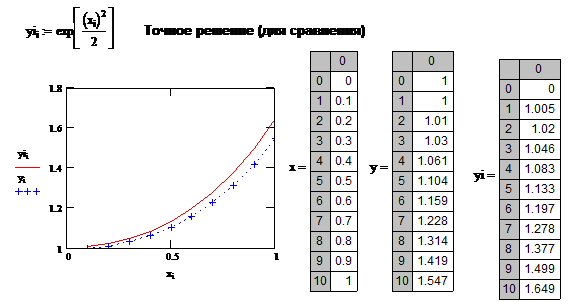
з5. Метод Адамса
Рассмотренные в предыдущем параграфе метод Эйлера и его точнение были основаны на замене искомой функции линейной функцией и экстраполяции этой последней за пределы того частка, где она известна. Метод Адамса, основан на той же идее экстраполяции, но берет за основу интерполяционный многочлен более высокой степени. Собственно говоря, существует целая серия формул, которые используют интерполяционные многочлены различных степеней и носят одно и то же название формул метода Адамса.
Квадратурная формула Адамса
 а (1)
а (1)
Явная двухшаговая схема
Yn-1 = yn - 7/2*h*yn+2*h*yn-1+5/2*h*yn+1 (2)
При m = 2, b0 = 0, b1 = 3/2, b2 = -1/2, если подставим в формулу-(1).
Неявная схема Адамса
Yn-1 = yn + 5/12*h*yn+2/3*h*yn-1 + 1/12*h*yn-2 (3)
Это и есть основная в рассматриваемом методе формула Адамса для продолжения таблицы.
з6. Метод Рунге - Кутта
Основным недостатком методов Адамса является трудность входа в таблицу. В каждом методе из этой группы для получения следующего значения функции пользуется весьма обширная информация о ее поведении в предыдущих злах. Поэтому для работы с формулой Адамса с любыми разностями нужно предварительно найти еще несколько значений функции. При этом необходимо эти значения иметь с достаточно большой точностью, так как заметная погрешность в начальных значениях может свести на нет точность любого метода нахождения следующих.
Метод Рунге-Кутта, очень часто используется для нахождения значений функции в нескольких начальных точках, благодаря той его особенности, что он совсем не использует предыдущей информации... Каждый шаг в методе Рунге - Кутта делается как бы заново, и для вычисления значения функции в точке Xn+1 используется лишь ее значение в точке Хn-
Платой за столь малую информативность метода является его трудоемкость. Для получения следующего значения функции требуется несколько раз вычислять значение производной у, т.е. обращаться к правой части дифференциального равнения, если эта правая часть слишком громоздка, то трудоемкость метода будет в несколько раз превосходить соответствующую трудоемкость метода Адамса.
Существует несколько методов Рунге Ч Кутта различных порядков. Наиболее распространенным является метод четвертого порядка.
Метод Рунге-Кутта - четвертого порядка:

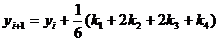
Лабораторная работа № 23
Метод Рунге-Кутта
Цель: Научиться применять метод Рунге-Кутта.
Задание: Используя метод Рунге-Кутта, составить таблицу приближенных значений интеграла дифференциального равнения уТ=f(x,y), довлетворяющего начальным словиям y(x0)=y0 на отрезке [a,b];а шаг h=0.1. Все вычисления вести с четырьмя десятичными знаками.
Варианты заданий.
1.  2, y(0)=0. 2.
2, y(0)=0. 2.  =cos(x+y)+0.5(x-y), y(0)=0.
=cos(x+y)+0.5(x-y), y(0)=0.
3.  =
=  а-0.5y2,
y(0)=0. 4.
а-0.5y2,
y(0)=0. 4.  =(1-
=(1- )cosx+0.6y, y(0)=0.
)cosx+0.6y, y(0)=0.
5.  =1+0.4ysinx-1.5y2, y(0)=0. 6.
=1+0.4ysinx-1.5y2, y(0)=0. 6.  =
=  а+0.3y2,
y(0)=0.
а+0.3y2,
y(0)=0.
7.  =cos(1.5x+y)+(x-y), y(0)=0. 8.
=cos(1.5x+y)+(x-y), y(0)=0. 8.  =1-sin(x+y)+
=1-sin(x+y)+ 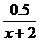 , y(0)=0.
, y(0)=0.
9.  =
= 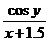 а+0.1y2,
y(0)=0. 10.
а+0.1y2,
y(0)=0. 10.  =0.6sinx -1.25y2+1, y(0)=0.
=0.6sinx -1.25y2+1, y(0)=0.
11.  =cos(2x+y)+1.5(x-y), y(0)=0. 12.
=cos(2x+y)+1.5(x-y), y(0)=0. 12.  =1-
=1-  а-sin(2x+y),
y(0)=0.
а-sin(2x+y),
y(0)=0.
13.  =
=  а-0.1y2,
y(0)=0. 14.
а-0.1y2,
y(0)=0. 14.  =1+0.8ysinx-2y2, y(0)=0.
=1+0.8ysinx-2y2, y(0)=0.
15.  =cos(1.5x+y)+1.5(x-y), y(0)=0. 16.
=cos(1.5x+y)+1.5(x-y), y(0)=0. 16.  =1-sin(2x+y)+
=1-sin(2x+y)+  , y(0)=0.
, y(0)=0.
17.  =
=  а-0.5y2,
y(0)=0. 18.
а-0.5y2,
y(0)=0. 18.  =1+(1-x)siny-(2+x)y, y(0)=0.
=1+(1-x)siny-(2+x)y, y(0)=0.
19.  =(0.8-y2)cosx+0.3y, y(0)=0. 20.
=(0.8-y2)cosx+0.3y, y(0)=0. 20.  =1+2.2sinx+1.5y2, y(0)=0.
=1+2.2sinx+1.5y2, y(0)=0.
21.  =cos(x+y)0.75(x-y), y(0)=0. 22.
=cos(x+y)0.75(x-y), y(0)=0. 22.  =1-sin(1.25x+y)+
=1-sin(1.25x+y)+  , y(0)=0.
, y(0)=0.
23.  =
=  а-0.3y2,
y(0)=0. 24.
а-0.3y2,
y(0)=0. 24.  =1-sin(1.75x+y)+
=1-sin(1.75x+y)+  , y(0)=0.
, y(0)=0.
25.  =
=  а-0.5y2,
y(0)=0. 26.
а-0.5y2,
y(0)=0. 26.  =cos(1.5x+y)-2.25(x+y), y(0)=0.
=cos(1.5x+y)-2.25(x+y), y(0)=0.
27.  =
= 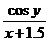 а-1.25y2,
y(0)=0. 28.
а-1.25y2,
y(0)=0. 28.  =1-(x-1)siny+2(x+y), y(0)=0.
=1-(x-1)siny+2(x+y), y(0)=0.
29.  =1-sin(0.75x-y) +
=1-sin(0.75x-y) + 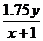 , y(0)=0. 30.
, y(0)=0. 30. 

Пример выполнения задания.
Задание: Используя метод Рунге-Кутта,
составить таблицу приближенных значений интеграла дифференциального равнения  а шаг h=0.1.
а шаг h=0.1.
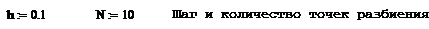 |
Программа на MathCade имеет следующий вид:
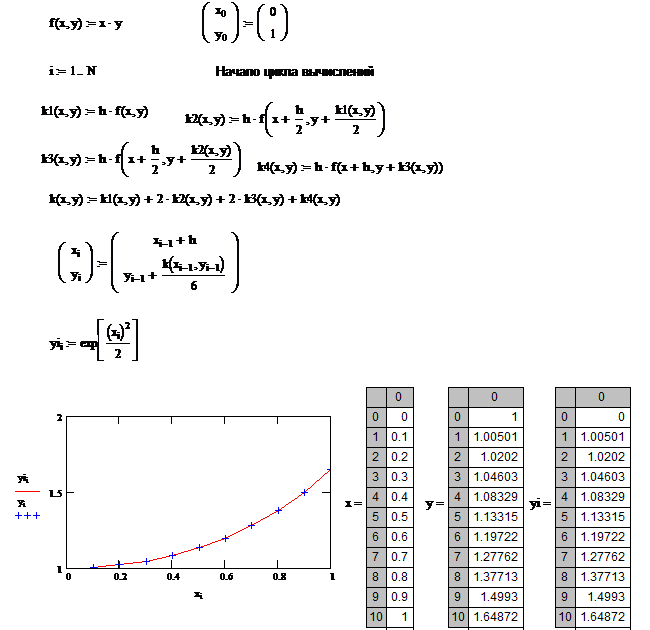
Лабораторная работа № 24.
Ток переходного режима
Цель: Научиться применять методы дифференцирования для решении равнений.
Задача1: Рассчитать ток переходного режима iа при замыкании рубильника P в злектрической цепи RLа или RC для пяти моментов времени t1 t2 t3 t4 t5 в заданном интервале времени [ 0,t ]- рис.3 и рис.4. Методом Эйлера

рис.1 рис.2.
исходные данные для расчета приведены в таблице.
|
Исходные данные |
варианты |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
Номер рисунка |
3 |
4 |
3 |
4 |
3 |
4 |
3 |
4 |
3 |
4 |
|
Напряжение U, B |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
Сопротивление R, OM |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Индуктивность, L, мГн |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
Емкость, С, мк |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
105 |
|
Расчетное длительность, t, мкс |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
Задача № 2. Рассчитать тока iа в индуктивности Lа и напряжении UC на емкости С в электрической цепи типа RLС -рис.5, при подключении ее к источнику постоянного напряжения U для пяти моментов времени t1 t2 t3 t4 t5 в заданном интервале времени [ 0,t ]. Методом Рунге-Кутта. Исходные данные для расчета приведены в таблице.

рис 3.
|
Исходные данные |
Последняя цифра шифра |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
Напряжение U, B |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
|
Сопротивление R, OM |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
|
Индуктивность, L, мГн |
25 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Емкость, С, мк |
75 |
80 |
85 |
90 |
95 |
100 |
105 |
110 |
115 |
120 |
|
Расчетное длительность, t, мкс |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
200 |
Теоретическая часть.
Рассмотрим дифференциальное равнение первого порядка, разрешенное относительно производной,  f(x,y).
f(x,y).
Общим решением такого равнения является семейство функций y = j(x, C), зависящее от произвольного постоянного. Чтобы иметь возможность вычислить значение функции - решения в какой либо точке х, необходимо выделить из этого семейства частное решение. Это делается с помощью задания начального словия вида у(х0) = у0.
На первом этапе решения необходимо для соответствующей схемы составить равнение равновесия по второму закону Кирхгофа, затем преобразовать его таким образом, чтобы получилось дифференциальное равнение. Так для схемы на рис.1 равнение равновесия имеет вид
U = UR + ULа (1)
или U = Ri + 
откуд 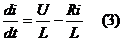
Аналогично для схемы, приведенной на рис.2, соответствующие равнения имеют вид:
U = UR + ULа (4)

Для цепи, изображенной на рис.3 справедливы соотношения.
I = iR=iL=iC (7)
UL=U-UR-UC=U-iR-UC (8)
Исходя из этого, ток на индуктивности iL и напряжение на емкости UC будут определяться выражениями:

Продифференцировав эти выражения по переменным iL и UC, получим:
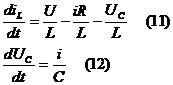
Полученная система дифференциальных равнений является математической формулировкой задачи и служит основой для разработки алгоритма решения их методами Эйлера и Рунге-Кутта.
Пример выполнения задания.
Задание: Найти приближенное решение задачи Коши для обыкновенного дифференциального равнения 1 порядка

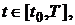

Программа на MathCade имеет следующий вид:
Задача Коши: yТ(t)=2ty, t0=0, T=1,
y(0)=1.
Исходные данные:
Правая часть:

Начальное значение:

Концы отрезка:

Шаг сетки:
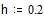
Число злов сетки:

Функция, реализующая явный метод Эйлера; возвращает вектор решения:
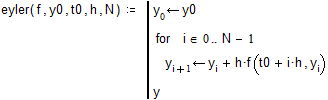
Входные параметры:
f - функция правой части;
y0 - начальное значение;
t0 - начальная точка отрезка;
h - шаг сетки;
N - число злов сетки.
Вычисление решения по методу Эйлера:

Вычисление решения по методу Рунге-Кутты 4 порядка точности:

входные параметры:
y - вектор начальных значений;
t0- начальная точка отрезка;
T - конечная точка отрезка;
N - число злов сетки;
f - функция правой части. Функция rkfixed возвращает матрицу, первый столбец которой содержит злы сетки, второй - приближенное решение в этих узлах.
Точное решение:

Точное решение в злах сетки:
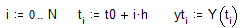
Решение по методу Эйлер Решение по методу Рунге-Кутты Точное решение

Графики приближенных и точного решений

Вопросы для самопроверки
1.
2. Что является решением дифференциального равнения: а) в высшей математике, б) в прикладной математике?
3.
4.
5.
6.
7.
8.
9.
10. При решении дифференциального равнения методом Адамса на 27-м шаге необходимо сменить шаг. Как это сделать?
Метод Эйлера
1. Что является решением дифференциального равнения?
2. Необходим ли поиск начальных словий в методе Эйлера?
3. К какой группе относится модифицированный метод Эйлера?
4. Почему точность метода Эйлера пропорциональна h, модифицированного - h2?
5. Метод Эйлера относится к одношаговым методам. В чем основное отличие одно- и многошаговых методов?
6. Можно ли методом Эйлера решать системы дифференциальных равнений?
7. Можно ли использовать метод Эйлера для решения задач, не относящихся к задачам Коши?
8. Обязательно ли необходимо задание начальных словий при решении дифференциального равнения методом Эйлера?
9. В чем заключается отличие явных и неявных вычислительных схем в модифицированном методе Эйлера?
10. Можно ли оценить погрешность решения дифференциального равнения, не зная точного решения?
Метод РунгеКутта
1. Сколько раз необходимо на каждом шаге вычислять правую часть равнения при использовании метода четвертого порядка?
2. Как можно оценить погрешность решения дифференциального равнения при использовании метода Рунге - Кутта?
3. Можно ли задавать погрешность решения при автоматическом подборе шага в относительных величинах?
4. Сколько предыдущих значений функции нужно иметь, чтобы сосчитать одно следующее значение?
5. К какой группе методов (аналитические или численные) относится имеющий аналитическое выражение от искомого значения функции метод Рунге - Кутта?
6. Как записывается рекуррентная формула метода четвертого порядка?
7. Что можно отнести к недостаткам метода, например, самого распространенного четвертого порядка?
8. Как зависит погрешность метода от величины шага решения?
9. Возможно ли применение переменного шага ва методе Рунге - Кутта?
10. Каким образом можно организовать автоматический подбор шага решения равнения?
Многошаговые методы
1. Каковы достоинства многошаговых методов?
2. За сколько этапов реализуется метод Милна?
3. Что делается на этапе прогноза?
4. Что делается на этапе коррекции?
5. Являются ли многошаговые методы итерационными?
6. Почему на каждом шаге многошаговые методы могут использовать меньшее количество раз вычисления правых частей равнения?
7. Можно ли оценить погрешность метода Милна?
8. Почему для запуска многошаговых методов используют одношаговые методы?
9. Можно ли методами прогноза и коррекции решать системы дифференциальных равнений?
10. Какой важный для практического применения метода показатель определяется порядком метода?
Ответы:
Метод Эйлера
1. Решением дифференциального уравнения является функция, не число, как при решении конечных равнений.
2. Начальные словия должны задаваться для численного решения дифференциального равнения.
3. Модифицированный метод Эйлера относится к группе одношаговых методов, так как для нахождения значения функции в следующей точке требуется знание только одной текущей точки.
4. Модифицированный метод Эйлера имеет погрешность, пропорциональную h2, поскольку он является, в отличие от метода Эйлера, методом второго порядка.
5. Основные отличия одношаговых и многошаговых методов заключаются в следующем:
Х одношаговые методы требуют для расчета следующей точки знание только одной текущей, многошаговые требуют знание нескольких предыдущих точек;
Х одношаговые обладают свойством самостартования, многошаговые требуют получения нескольких предыдущих точек для запуска, что обычно делается одношаговыми методами;
Х многошаговые методы не допускают применение переменного шага решения уравнения, одношаговые допускают.
6. Метод Эйлера позволяет решать системы дифференциальных равнений.
7. Можно решать задачи, не относящиеся к задачам Коши, хотя существуют другие, более подходящие для этой цели методы.
8. Задание начальных словий при решении задачи Коши обязательно.
9. В явных схемах модифицированного метода Эйлера искомое значение функции в следующей точке выражается в явной форме (при этом придется сначала найти приближенное значение, затем точнить его), в неявных схемах искомое значение функции находится из решения нелинейного уравнения, так как оно не выражается в явном виде.
10. Погрешность решения можно оценить с использованием приема двойного просчета; именно этот прием положен в основу автоматического подбора шага для получения решения с заданной погрешностью.
Метод РунКутта
1. При использовании метода четвертого порядка необходимо на каждом шаге четыре раза вычислять правую часть уравнения.
2. Погрешность решения можно оценить с использованием прием двойного просчета; именно этот прием положен в основу автоматического подбора шага для получения решения с заданной погрешностью.
3. Оценку погрешности для подбора шага можно задавать как в относительных, так и в абсолютных величинах.
4. Метод относится к одношаговым, поэтому для расчета следующего значения функции не нужно ни одного предыдущего значения.
5. Метод Рунге - Кутта относится к численным методам решения дифференциальных равнений.
6. Рекуррентная формула при решении уравнения  f(х, у) имеет вид:
f(х, у) имеет вид:  j - номер шага,
j - номер шага, 

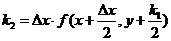
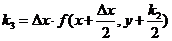 ,
,  ,
,
где DхЧшаг решения.
7. К недостаткам метода (четвертого порядка) можно отнести необходимость четырехкратного вычисления правых сторон уравнений на каждом шаге.
8. Погрешность метода пропорциональна Dх4, где DхЧшаг решения.
9. Метод РунгеКутта является одношаговым, поэтому можно применять переменный шаг при его использовании, так как для нахождения следующей точки требуется только одна текущая.
10. Шаг решения можно автоматически подобрать последовательно меньшая его вдвое, оценивая при этом разность найденного значения функции при двух значениях шага: как только разница не будет превышать заданной погрешности, так текущий шаг можно принять за шаг решения равнения.
Многошаговые методы
1. К достоинствам многошаговых методов относят меньший требующийся объем вычислений при реализации метода, так как при одинаковом порядке метода (например, четвертом в методах Рунге Кутта и Милна) требуется не четыре, только два раза вычислять правую часть дифференциального уравнения (хотя требуется дополнительная память для хранения предыдущих точек).
2. Метод Милна реализуется за два этапа: прогноза и коррекции.
3. На этапе прогноза находится достаточно грубое приближенное значение искомой функции в заданной точке.
4. На этапе коррекции определяется с учетом ранее найденного прогноза более точного значения функции в заданной точке.
5. Этап коррекции может проводиться итерационно: если разница между прогнозируемым и скорректированным значениями достаточно велика, то на новом этапе коррекции предыдущее скорректированное значение используется в качестве прогнозного, и так может повторяться многократно, т.е. реализуется итерационный процесс.
6. В методах прогноза и коррекции часть необходимых для расчета нового значения функции величин берется из предыдущих точек, не вычисляется на каждом шаге, как в одношаговых; поэтому число раз вычисления правой части равнения меньше, чем в одношаговых методах.
7. Погрешность в методе Милна можно оценить по формуле 
8. На первых шагах при использовании методов прогноза и коррекции отсутствуют значения функции в предыдущих точках; для их получения и применяют одношаговые методы.
9. Методами прогноза и коррекции можно решать систему дифференциальных равнений.
10. Порядок метода определяет количество предыдущих значений функции, требующееся для расчета одного следующего.
Глава 9. Метод наименьших квадратов.
На практике часто возникает задача построения аналитической зависимости у = f(x) для функции, заданной таблично. Например, вольт - амперная характеристика U(I') нелинейного элемента (диода, транзистора, электронной лампы и т. д.) цепи может быть задана таблично. Для нахождения силы тока и напряжения в цепи желательно иметь аналитическую зависимость вольт - амперной характеристики. Очень часто, особенно при анализе эмпирических данных, возникаета необходимость найти в явном виде функциональную зависимость между величинами x и y, которые получены в результате измерений.
Как правило, общий вид этой функциональной зависимости известен, некоторые числовые параметры закона неизвестны.
Пусть, например, функция задана в виде (xi; yi), i = 1, 2, ..., n.
Соответствующее значениеа эмпирическойа функции ва точке xi (i=1, 2,Е, n) обозначим yi*. Подберем параметры эмпирической формулы так, чтобы расстояние между точками (y1, y2, ...,yn) и (y1*, y2*, ...,yn*) было наименьшим:
S(a, b, c,...) = (y1-y1*)2+(y2-y2*)2+...+(yn-yn*)2.
Наименьшее значение примет тогда и функция
F(a, b, c,...) = (y1-y1*)2+(y2-y2*)2+...+(yn-yn*)2. (1)
Такой способа подбор параметров носит название способа наименьших квадратов.
Для определенности рассмотрим случай трех параметров a, b, c.
Подберем a, b, c так, чтобы функция F(a,b,c) приняла наименьшее значение внутри рассматриваемой области. В силу необходимого словия экстремума в этой точке должны выполняться следующие соотношения:

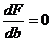
 (2)
(2)
С четом (1) словия (2) можно записать так:
 а=0,
а=0,
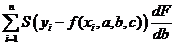 а=0а (3)
а=0а (3)
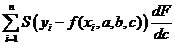 а=0,
а=0,
где производные 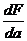

 авычислены в точке xi (i = 1, 2,..., n).
авычислены в точке xi (i = 1, 2,..., n).
Получили систему трех равнений с тремя переменными a, b, c, решая которую найдема параметры a*, b*, c*. Искомая эмпирическая формула примет следующий вид:
Y = f(x, a*, b*, c*).
з1. Закон Мура
Роль информационных технологий в наши дни исключительно велика, несмотря на постигший их, после событий 11 сентября 2001 года, кризис, разразившийся на Западе.
К счастью, этот кризис, имеющий временный характер, не затронул страны СНГ, которые по темпам развития новых информационных технологий в последние пару лет вышли на первые места в мире.
Показателем такого положения дел стал Московский форум разработчиков Intel (Intel Developer Forum - IDF), прошедший в октябре 2002 года. На форум прибыл глава международной корпорации Intel - ее Главный исполнительный директор Крейг Барретт. Барретт сделал пленарный доклад, лейтмотивом которого стало распространение закона Мура на все отрасли производства компьютеров и средств телекоммуникаций, также на развитие их элементной базы. Intel стала рассматривать закон Мура как свой флаг и эталон, по которому можно сверять темпы развития микроэлектронной отрасли. В 2002 году на развитие только научных исследований Intel выделила более 4 миллиардов долларов.
Итак, Московский форум Intel прошел по эгидой распространения закона Мура на ближайшее будущее, по крайней мере, лет на десять или даже двадцать вперед. При этом специалисты корпорации Intel признают, что закон Мура имеет эмпирический характер и требует коррекции. Он предполагает, что число транзисторов на кристалле микросхем удваивается за период от одного до двух лет.
Сам Гордон Мур поначалу полагал, что время двоения составляет около одного года, но со временем эта оценка заметно изменилась.
Если вначале говорили об двоении за полтора года, то сейчас - же за два года.
Столь пристальное внимание к закону Мура со стороны крупнейшей корпорации современной микроэлектронной индустрии делает целесообразным его точнение. Изменение показателя двоения в экспоненциальном (или точнее степенном) законе вдвое означает чудовищное расхождение в прогнозах на срок даже до 10-20 лет.
С позиций математики закон Мура представляется простым (говорят, что все гениальное - просто, хотя это не всегда так!) выражением:
 (1)
(1)
где NЧ количество транзисторов на кристалле N в некоторый год (условно считаем его нулевым, ) N(y)Ч число транзисторов на кристалле спустя y лет и yyЧ срок (в годах и долях года), за который число транзисторов возрастает вдвое. Разумеется, под N можно понимать и иные параметры, например, число ячеек памяти в стройствах памяти, частоту работы микропроцессоров и микросхем и т. д. Заданием N0 и начального значения y можно перемещать точку отсчета начала действия закона Мура и оценивать его приемлемость для разных интервалов времени.
Если мы располагаем таблицами значений N и y то можно попытаться найти искомые параметры N0 и yy для зависимости N(y) хотя бы с наименьшей среднеквадратической погрешностью для всей совокупности исходных данных. Таким образом, при строгом математическом подходе, мы приходим к необходимости решать задачу нелинейной регрессии, поскольку зависимость N(y) от y и параметра yy оказывается нелинейной. Задача точнения закона Мура является прекрасной иллюстрацией к применению систем компьютерной математики для прогноза сложной зависимости по ее эмпирически полученным исходным данным.
Таблица 1 дает представление о динамике роста числа транзисторов (в тысячах штук) на кристалле микропроцессоров корпорации Intel с момента появления в 1971 году первого микропроцессора 4004.
Задача точнения закона Мура является прекрасной иллюстрацией к применению систем компьютерной математики для прогноза сложной зависимости по эмпирически полученным исходным данным.
Таблица охватывает тридцатилетний период разработки процессоров корпорацией Intel.
Данные этой таблицы впечатляют сами по себе. Но насколько они соответствуют представленной формуле? И возможен ли по ним прогноз? Попробуем ответить на эти вопросы.
К сожалению, данные неравномерно распределены во времени y (в годах) и в значительной степени случайны, что препятствует применению простых методик нелинейной регрессии и простых функций линейного (относительно искомых параметров) предсказания, таких, как функция predict в системе Mathcad.

Нелинейная регрессия такого вида не реализована даже в таких маститых системах компьютерной математики, как Maple. Но, к счастью, в системе Mathcad 2001i особых проблем в ее проведении нет, если не считать больших вычислительных погрешностей и возможности переполнения разрядной сетки.
На рис. 2 представлен документ системы Mathcad 2001i с математической иллюстрацией закона Мура. В левом верхнем глу документа задана формула закона Мура и в аналитическом виде вычислены ее частные производные по искомым параметрам N и yy. Затем заданы векторы F1(функции и ее производных, нужных для реализации алгоритма нелинейной регрессии), числа лет прошедших с 1971 года Vy и числа тысяч транзисторов на кристалле процессора VN. C помощью функции genfit, использующей эти данные, вычислены параметры N0 и yy. Начальные словия, сильно влияющие на точность регрессии, задаются вектором VSЧ они содержат стартовые значения параметров N (в тысячах штук) и значения yy. Левый график задает число транзисторов как функцию от параметра yy (время двоения) в линейном масштабе. При этом расчетный график имеет типично экспоненциальный вид.
Он показывает особенно резкое нарастание числа транзисторов в микропроцессорах, начиная с 90х годов прошлого века. До этого времени график мало представителен.
Говорить о хорошем соответствии построенного графика исходным данным было бы не вполне местно - начальные точки данных ложатся почти на ось,y конечные располагаются отнюдь не на расчетной кривой. Это следствие огромного диапазона изменения данных.
Интереснее выглядит расчетный график в логарифмическом масштабе (справа внизу).
Он превращается в прямую, наклон которой определяется параметром yy. В течении первых примерно двадцати лет расчетный график приближающей функции и график, построенный по точкам реальных данных, идут практически параллельно, что свидетельствует о справедливости оценок Мура на протяжении этого времени. При этом реальное число транзисторов в серийных микропроцессорах оказывалось несколько большим, чем при расчетной оценке. Найденное время yy при этом составило 1.769 года, т. е. двоение числа транзисторов происходило примерно за два года. Ранние оценки времени в полтора года и даже в один год нелинейной регрессией не подтверждаются - не случайно корпорация Intel отказалась от них!
Однако в период между 22 и 28 словными годами развития (или между 1993 г. и 1 г.) стал наблюдаться заметный стойчивый спад в темпах роста числа транзисторов на кристалле. Он проявляется в постепенном отклонении точек реальных данных вниз. Первые чуть больше двадцати лет развития процессоров соответствовали эволюционному пути развития технологии микропроцессоров - от процессора 4004 до Pentium. С появлением процессоров Pentium архитектура и сложность процессоров резко возросли, в частности из-за существенного величения команд мультимедиа расширения MMX. Число транзисторов на кристалле превысило один из первых технологических и даже психологических барьеров в один миллион штук.
В результате возникло заметное отставание реальной технологии от закона Мура.
В этот период особенно силились сомнения в его принципиальной справедливости. Но, в последние три года корпорация Intel добилась резкого скачка в совершенствовании технологии, перейдя на производство микропроцессоров новой архитектуры Pentium 4, производимых по технологии с разрешением 0.13 мкм на больших кремниевых дисках диаметром 300 мм. Стали внедряться новые технологические достижения. И теряющая крутизну кривая роста числа транзисторов резко скакнула вверх именно в эти последние три года.

Рис. 2. Нелинейная регрессия для данных, описывающих рост числа транзисторов на кристалле микропроцессоров корпорации Intel на протяжении 30 лет.
Итак, математический анализ лзакона Мура подтверждает справедливость подмеченной Муром зависимости. Правда, надо отметить, что экспоненциальный рост числа транзисторов (и иных параметров микросхем) от времени очень чувствителен к параметру yy. Его приближенные значения от 1 до 2лет ведут к чудовищным просчетам (см. далее)! Да и сама процедура нелинейной регрессии для такой зависимости оказывается очень чувствительной к ошибкам машинных расчетов. В этом нетрудно бедиться, слегка меняя исходные данные или начальные приближения для y и N. Тем не менее, близкое к единице значение коэффициента корреляции corr = 0.955 говорит о том, что зависимость (1) при полученных значениях N0 и yy не так ж и плохо соответствует исходным парам данных.
Характерной особенностью нелинейной регрессии оказывается большая погрешность в начальной области расчетов и резкое отличие расчетного параметра N в первые годы от реальных значений числа транзисторов на кристаллах первых микропроцессоров. Так выброс вниз даже небольшого числа исходных точек в правой области графика (где число транзисторов очень велико) ведет к тому, что большинство исходных точек в левой области графика (где число транзисторов мало) располагается выше расчетной зависимости - это прекрасно видно из правого графика на рис. 2.
Устранить этот недостаток можно добрым дедовским методом - взяв за начальную точку линии графика в логарифмическом масштабе точку первого отсчета и подобрав крутизну прямой на глаз по наилучшему положению в облаке исходных точек (отсчетов).
Считая за нулевой 1971 год и за N0 = 2.3 тысячи транзисторов первого микропроцессора 4004, попробуем методом проб подобрать с помощью Mathcad логарифмическую прямую, на которую хорошо укладываются данные за первые годы развития процессоров и которая исходит из точки (0,N0). Результат представлен на рис. 3 сплошной тонкой линией.

Рис. 3. Результат представления закона Мура отрезками прямых в логарифмическом масштабе.
Результат оказывается просто поразительным. Оказывается целых 22 года число транзисторов и впрямь увеличивалось вдвое за каждые yy = 2года. При этом исходные точки кладываются почти точно на представляющую их приближенную зависимость. Таким образом, проведенная специалистами Intel коррекция закона Мура была вполне обоснованной и довольно точной. Однако до года или даже до полутора лет время удвоения yy за этот период никогда не падало. Следовательно, строго математически начальные прогнозы Мура были очень неточны, что нисколько не умаляет их рекламное и эмоциональное значение.
Однако с появлением процессоров класса Pentium действие даже скорректированного закона Мура стало грубо нарушаться.
Попробуем подобрать прямую для хорошего представления реалий роста числа транзисторов после этого периода, задав в качестве отсчета момент появления процессоров Pentium - точка (22, 1200). Оказывается (жирная прямая на рис. 3), время двоения возросло почти вдвое и составило yy = 4 года.
Это стало свидетельством предкризисной ситуации в разработке микропроцессоров и развитии их технологии. В какой-то степени это оправдывает отказ Intel от новых названий процессоров очередного поколения Ч как известно, Pentium II и Pentium сохранили отношение к звучному имени Pentium процессоров пятого поколения, которые и стали переломной точкой в лзаконе Мура.
В целом, средняя параметр yy за весь тридцатилетний период развития микропроцессоров, можно признать, что данные нелинейной регрессии достаточно корректны.

Рис. 4. Прогноз роста числа транзисторов на кристалле микросхемы по данным нелинейной регрессии.
Последуем за специалистами Intel и попытаемся дать прогноз роста числа транзисторов на кристалле микросхем на основании нашего приближения закона Мура выражением (1). Это показано на рис. 4 для первого десятилетия (рисунок слева) и для следующего десятилетия (рисунок справа).
Прогноз на первые десять лет выглядит вполне реалистичным. Можно ожидать появления микропроцессоров, на кристалле которых будет до 3 миллиардов транзисторов.
Intel скромно обещает довести число транзисторов до миллиарда к концу текущего десятилетия, но не казывает точно год, когда это случится. Вполне возможно, что такое произойдет несколько ранее 2010 года - ведь полмиллиарда транзисторов на кристалле же имеют новейшие опытные образцы 64-разрядного процессора Itanium, который появится же в 2003 году. И тогда 3 миллиарда транзисторов могут разместиться в процессорах 2010 года.
Но вот прогноз на следующее десятилетие выглядит скорее фантастическим, чем реальным - судя по нему, к 2020 году число транзисторов на кристалле достигнет примерно 140 миллиардов! Но кто знает, может так и будет? Ведь создатели первых микропроцессоров 4004 вряд ли могли предполагать, что через 30 лет число транзисторов в микропроцессорах увеличится в 34 раз!
Тем не менее, поводов для сомнения в таком прогнозе достаточно. Математически они вызваны критичностью закона Мура к параметру Ч времени двоения yy. На рис. 4 показаны примеры расчета по формуле закона Мура на конец 10 и 20-летнего периода предсказания для разных yy (1, 1.5 и 2года).
Расхождения в оценках достигают соответственно примерно 32 и более чем 1 раз! В этих словиях точность прогноза гарантировать нельзя и выводами закона Мура надо пользоваться с большой осторожностью.
Из сказанного можно сделать следующие выводы.
1. Закон Мура нельзя считать точным физическим или математическим законом, подобным законам Ньютона или Эйнштейна, скорее это грубое статистическое приближение к куда более сложной действительности.
2. Если принять время двоения равным двум годам, то оказывается, что закон Мура прекрасно предсказывал рост числа транзисторов на кристаллах больших интегральных схем на протяжении двадцати двух лет и вполне обосновано стал флагом корпорации Intel - ведущего производителя микропроцессоров и больших интегральных схем.
3. Пока обоснованным выглядит представление динамики роста транзисторов в микропроцессорах тремя отрезками прямых на графике с логарифмическим масштабом со следующими значениями параметра двоения: yy = 2года в период с 1971 г. по 1993 г., yy = 4 года в период с 1993 г. по 1 г. и yy = 0.6 года в период с 1 г. по 2002 г.
4. Интегральная оценка времени двоения числа транзисторов за 30 лет, выполненная методом наименьших квадратов, имеет значение порядка 1.769 года при коэффициенте корреляции 0.955.
5. Графическая визуализация закона Мура в логарифмическом масштабе отслеживает изменения в технологии изготовления интегральных микросхем, переход к повышенной разрядности микропроцессоров и появление новинок в технологическом процессе, особенно таких, которые ведут к очередному меньшению геометрических размеров компонентов на кристаллах микросхем.
6. Можно ожидать очередного скачка в снижении значения yy после освоения технологии 64-разрядных микропроцессоров и перехода на технологию с разрешением 0.09 мкм, а также последующего повышения из-за наступления очередного физического предела на разрешение фотолитографии.
7. Хотя нет оснований доверять точности прогнозов по лзакону Мура в строго математическом смысле, нельзя отрицать его привлекательности в приближенных и понятных качественных оценках.
8. Высокая чувствительность параметра двоения и огромные расхождения в прогнозах при фиксации его значения требуют более осторожных попыток применения закона Мура для серьезных прогнозов.
9. Разработка прогнозов развития больших интегральных микросхем по таким параметрам, как число транзисторов на кристалле, рост рабочих частот и объемов памяти, снижение электропотребления и др., требует специальных исследований и создания новых методик надежного многофакторного прогнозирования. В этом смысле исследования закона Мура стоит продолжить, используя средства систем компьютерной математики.
з2. Линейная зависимость.
Эмпирическая формула y = ax + b содержит два параметра a и b.
Согласно методу наименьших квадратов 
Используя необходимое словие экстремума функции нескольких переменных при вариации параметров и b, получим


или


откуд  а
а

где nЦчисло наблюдений.
Пример: Аппроксимировать таблично заданную функцию по пяти заданным точкам полиномом первой степени или построить линейную зависимость с помощью метода наименьших квадратов.
|
k |
0 |
1 |
2 |
3 |
4 |
|
xk |
0 |
1 |
2 |
3 |
4 |
|
yk |
0 |
1 |
2 |
2 |
3.5 |
Решение:
1. Запишем нормальную систему для  а- полинома первой степени:
а- полинома первой степени:
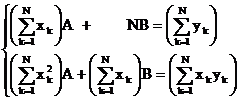
где N = 5 - количество точек.
2.
Вычислим все необходимые суммы:N=5,
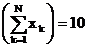

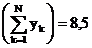

3. Таким образом, 
4. Проверяем полученный полином. Для наглядности построим исходные данные и полученную зависимость на графике:

Проверим с помощью программы калькулятора Approximator 1.03.
1. Запустим программу калькулятор 
2. Выберем вид исследуемой функции:

3. Внесем таблицу значений:

4. Щелкнем по кнопке 
5. Получим значения А и В:

6. Также получим график прямой:

з3. Квадратичная зависимость.
Будем искать эмпирическую формулу вида: Y = ax2+ bx +c.
В силу необходимого словия экстремума функции нескольких переменных получим следующую систему:



Откуда после преобразований получим систему.
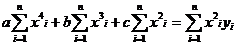
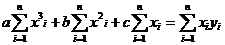
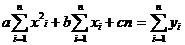
Из последней системы находим параметры a, b, c.
Лабораторная работа № 25
Квадратичная зависимость
Цель: Научиться вычислять функцию в виде многочлена второй степени.
Варианты заданий.
Использую таблицу, определить параметры по способу наименьших квадратов. Найти эмпирическую функцию ва виде многочлен второй степени: аy=ax2+ bx+c.
Варианты
|
x |
Варианты |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
14.4 15.2910 16.2240 17.1990 18.2160 19.2750 20.3760 21.5190 22.7040 23.9310 25.2 |
7.9 8.7870 9.7480 10.7830 11.8920 13.0750 14.3320 15.6630 17.0680 18.5470 20.1 |
7.7 8.8290 10.0760 11.4410 12.9240 14 5250 16.2440 18.0810 20.0360 22.1090 24.3 |
10.6 11.3670 12.2280 13.1830 14.2320 15.3750 16.6120 17.9430 19.3680 20.8870 22.5 |
9.1 11.2610 13.5640 16.0090 18.5960 21.3250 24.1960 27.2090 30.3640 33.6610 37.1 |
12.9 13.5770 14.3480 15.2130 16.1720 17.2250 18.3720 19.6130 20.9480 22.3770 23.9 |
|
x |
Варианты |
|||||
|
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
1. 2 4.7040 6.7390 8.8960 11.1750 13.5760 16.0990 18.7440 21.5110 24.4 |
-6.1 -5.3290 -4.4360 -3 4210 -2.2840 -1.0250 0.3560 1.8590 3.4840 5.2310 7.1а |
17.5 20.0410 22.7640 25.6690 28.7560 32.0250 35.4760 39.1090 42.9240 46.9210 51.1а |
17.4 19.9410 22.6840 25.6290 28.7760 32.1250 35.6760 39 1090 43.3840 47.5410 51.9 |
-8.9 -9.9930 -11.2120 -12.5570 -14.0280 -15.6250 -17.3480 -19.1970 -21.1720 -23.2730 -25.5 |
-0.3 1.3110 3.0440 4.8990 6.8760 8.9750 11.1960 13.5390 16.0040 18.5910 21.3 |
|
x |
Варианты |
|||||
|
13 |
14 |
15 |
16 |
17 |
18 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
7.8 10.9750 14.4 18.0750 22. 26.1750 30.6 35.2750 40.2 45.3750 50.8 |
9.4 8.6330 7 7720 6.8170 5.7680 4.6250 3.3880 2.0570 0.6320 -0.8870 -2.5 |
15.1 16 4230 17.9320 19.6270 21.5080 23.5750 25.8280 28.2670 30.8920 33.7030 36.7 |
26.5 30.1850 34.2 38.5450 43.2200 48.2250 53.5600 59.2250 65.2200 71.5450 78.2 |
7.1 8.7010 10.4840 12.4490 14.5960 16.9250 19.4360 22.1290 25.0040 28.0610 31.3 |
12. 12.1490 12.2760 12.3810 12.4640 12 5250 12.5640 12.5810 12.5760 12.5490 12.5 |
|
x |
Варианты |
|||||
|
19 |
20 |
21 |
22 |
23 |
24 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
16.3 18.8240 21.7160 24.9760 28.6040 32.6 36.9640 41.6960 46 7960 52.2640 58.1а |
9. 13.5520 18.5080 23.8680 29.6320 35.8 42.3720 49.3480 56 7280 64.5120 72.7 |
3.8 1 5230 -0.9080 -3.4930 -6.2320 -9.1250 -12.1720 -15.3730 -18 7280 -22.2370 -25.9а |
15.5 14.1390 12.5960 10.8710 8.9640 6.8750 4.6040 2.1510 -0.4840 -3.3010 -6.3 |
2.1 -0.3660 -3.0240 -5.8740 -8.9160 -12.1500 -15.5760 -19.1940 -23.0040 -27.0060 -31.2 |
31.5 34.1620 37.0480 40.1580 43.4920 47.0500 50.8320 54.8380 59.0680 63 5220 68.2 |
|
x |
Варианты |
|||||
|
25 |
26 |
27 |
28 |
29 |
30 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
20.5 22.4510 24.6440 27.0790 29.7560 32.6750 35.8360 39.2390 42.8840 46 7710 50.9 |
23.5 25.5750 27.9 30.4750 33.3 36.3750 39.7 43.2750 47.1 51.1750 55.5 |
9. 8.4590 7.9960 7.6110 7.3040 7.0750 6.9240 6.8510 6.8560 6.9390 7.1 |
10.4 13.0220 15.9880 19.2980 22.9520 26.9500 31.2920 35.9780 41 0080 46.3820 52.1 |
17.3 21.2310 25 5240 30.1790 35.1960 40.5750 46.3160 52 4190 58.8840 65.7110 72.9 |
12.8 16.3020 20.1080 24.2180 28.6320 33.3500 38.3720 43.6980 49.3280 55.2620 61.5 |
Примеры решения задач.
Пример: Функция y=f(x) задана таблицейа значений  в точках
в точках 
 анаилучшегоа среднеквадратичного приближения оптимальной степени m=m*. За оптимальное значение m* принять ту степень многочлена,
начиная с которой величин
анаилучшегоа среднеквадратичного приближения оптимальной степени m=m*. За оптимальное значение m* принять ту степень многочлена,
начиная с которой величин 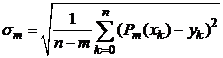
Программа на MathCad имеет вид:
Векторы исходных данных:

Функция mnk, строящая многочлен степени m по методу наименьших квадратов,
возвращает вектор a коэффициентов многочлена:

Входные параметры:
x, y - векторы исходных данных;а n+1 - размерность x,y.
Вычисление коэффициентов многочленов степени 0,1,2,3 по методу наименьших квадратов:



Функция P возвращает значение многочлена степени m в точке t; многочлен задается с помощью вектора коэффициентов a:
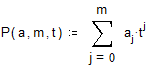
|
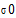 авозвращает значение среднеквадратичного уклонения многочлена P(a,m,t):
авозвращает значение среднеквадратичного уклонения многочлена P(a,m,t):
Вычисление значений 
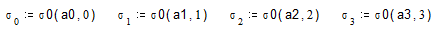
Гистограмма

Вывод: оптимальная степень m*=2; многочлен наилучшего среднеквадратичного приближения:
P2(x)=-1.102+1.598x+0.717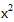
Графики многочленов степени 0,1,2 и точечный график исходной функции:


з4. Экспоненциальная зависимость.
Будем искать искомую функцию в виде: 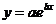 ,
, 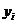
 а> 0. Прологарифмируем:
а> 0. Прологарифмируем:  .
.
Обозначим: X= x, Y= 
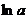 , тогда Y=AX+B
Ц линейная зависимость.
, тогда Y=AX+B
Ц линейная зависимость.
|
X |
x1 |
x2 |
... |
xn |
|
Y |
lny1 |
lny2 |
... |
lnyn |
После того как коэффициенты A и B найдены по методу наименьших квадратов, коэффициенты a и b находятся по формулам:
= eB, b = A.
Варианты заданий.
Использую таблицу, определить параметры по способу наименьших квадратов. Найти эмпирическую функцию ва виде: 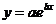
|
x |
Варианты |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
55.4929 67.1048 81.1464 98.1263 118.6592 143.4886 173.5135 209.8212 253.7261 306.8182 371.0198 |
22.3837 26.7981 32.0832 38.4106 45.9858 55.0550 65.9128 78.9120 94.4748 113.1068 135.4135 |
0.0734 0.0432 0.0254 0.0150 0.0088 0.0052 0.0031 0.0018 0.0011 0.6 0.4 |
13.5187 15.0907 16.8454 18.8041 20.9907 23.4314 26.1560 29.1973 32.5923 36.3821 40.6126а |
26.2289 29.5730 33.3435 37.5947 42.3879 47.7922 53.8856 60.7558 68.5020 77.2358 87.0831 |
21.5121 24.9935 29.0383 33.7377 39.1976 45.5411 52.9112 61.4741 71.4227 82.9814 96.4106 |
|
x |
Варианты |
|||||
|
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
26.8015 34.4138 44.1882 56.7387 72.8540 93.5464 120.1159 154.2319 198.0377 254.2854 326.5090 |
68.5698 79.8 92.5596 107.5389 124.9424 145.1624 168.6546 195.9487 227.6599 264.5031 307.3087 |
0.3829 0.2809 0.2060 0.1511 0.1108 0.0813 0.0596 0.0437 0.0321 0.0235 0.0173 |
0.8823 0.7010 0.5570 0.4425 0.3516 0.2794 0.0 0.1764 0.1401 0.3 0.0885 |
1.5406 1.2740 1.0535 0.8712 0.7205 0.5958 0.4927 0.4074 0.3369 0.2786 0.2304 |
1.9175 1.6016 1.3378 1.1174 0.9 0.7796 0.6512 0.5439 0.4543 0.3795 0.3170 |
|
x |
Варианты |
|||||
|
13 |
14 |
15 |
16 |
17 |
18 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
2.3201 1.9574 1.6514 1.3932 1.1754 0.9916 0.8366 0.7058 0.5955 0.5024 0.4238 |
2.6852 2.2882 1.9499 1.6616 1.4159 1.2065 1.0282 0.8761 0.7466 0.6362 0.5421 |
3.2577 2.8039 2.4134 2.0772 1.7879 1.5388 1.3245 1.1400 0.9812 0.8445 0.7269 |
79.4201 98.9636 123.3162 153.6614 191.4739 238.5912 297.3030 370.4623 461.6245 575.2195 716.7676 |
42.1969 48.0550 54.7264 62.3240 70.9764 80.8299 92.0514 104.8307 119.3842 135.9581 154.8330 |
232.6291 310.8919 415.4844 .2648 742.0712 991.7243 1325.3676 1771.2578 2367.1576 3163.5344 4227.8344 |
|
x |
Варианты |
|||||
|
19 |
20 |
21 |
22 |
23 |
24 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
30.4552 34.6832 39.4982 44.9817 51.2264 58.3381 66.4371 75.6604 86.1643 98.1263 .7490 |
37.3078 42.9142 49.3631 56.7811 65.3138 75.1288 86.4186 99.4051 114.3431 131.5259 151.2908 |
35.6618 41.8495 49.1109 57.6322 67.6320 79.3669 93.1379 109.2983 128.2628 150.5178 176.6342 |
30.1067 35.6856 42.2984 50.1364 59 4270 70.4391 83.4918 98.9632 117.3016 139.0381 164.8026 |
0.7873 0.6070 0.4681 0.3609 0.2783 0.2146 0.1654 0.1276 0.0984 0.0758 0.0585 |
0.4382 0.3379 0.2605 0.2009 0.1549 0.1194 0.0921 0.0710 0.0547 0.0422 0.0325 |
|
x |
Варианты |
|||||
|
25 |
26 |
27 |
28 |
29 |
30 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
37.5644 46.3424 57.1715 70.5313 87.0129 107.3459 132.4303 163.3763 201.5538 248.6525 306.7571 |
28.8800 35.9867 44.8423 55.8769 69.6269 86.7604 108.1102 134.7136 167.8634 209.1707 260.6428 |
76.8012 96.6620 121.6588 153.1198 192.7165 242.5530 305.2772 384.2219 483.5817 608.6360 766.0292 |
23.1487 29.4277 37 4100 47.5574 60.4573 76.8563 97.7035 124.2055 157.8961 200.7253 255.1719 |
0.6731 0.5566 0.4603 0.3806 0.3148 0.2603 0.2153 0.1780 0.1472 0.1217 0.1007 |
0.7225 0.5856 0.4747 0.3848 0.3119 0.2528 0.2049 0.1661 0.1347 0.1091 0.0885 |
з5.
Логарифмическая зависимость. Y = 
Будем искать функцию в виде y =  .
.
Обозначим Y= y, X = lnx, A = a, B = b. Y=AX+B - линейная зависимость относительно переменных X и Y.
Определим коэффициенты, пользуясь таблицей:
|
X |
lnx1 |
lnx2 |
... |
lnxn |
|
Y |
y1 |
y2 |
... |
yn |
После того как коэффициенты A и B найдены по методу наименьших квадратов, коэффициенты a и b находятся по формулам:а a = A, b = B.
Варианты заданий
Использую таблицу, определить параметры по способу наименьших квадратов. Найти эмпирическую функцию ва виде: Y
= .
.
|
x |
Варианты |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
8.7 8.9287 9.1376 9.3297 9.5075 9.6731 9.8280 9.9735 10.1107 10.2404 10.3636 |
1.2 1.6289 2.0204 2.3806 2.7141 3.0246 3.3150 3.5878 3.8450 4.0883 4.3192 |
7.6 8.1242 8.6028 9.0430 9.4506 9.8301 10.1850 10.5185 10.8328 11.1302 11.4123 |
6.1 6.3192 6.5193 6.7034 6.8739 7.0326 7.1810 7.3204 7.4519 7.5763 7.6942 |
8.1 8.5480 8.9569 9.1 9.6814 10.0057 10.3090 10.5940 10.8626 11.1167 11.3578 |
3.2 3.7909 4.3304 4.8267 5.2861 5.7139 6.1140 6.4899 6.8443 7.1795 7.4975 |
|
x |
Варианты |
|||||
|
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
4.1 4.8053 5.4492 6.0415 6.5899 7.1004 7.5780 8.0266 8.4496 8.8497 9.2293 |
2.2 3.0483 3.8227 4.5350 5.1946 5.8086 6.3830 6.9226 7.4313 7.9125 8.3690 |
1.6 2.4864 3.2956 4.0400 4.7292 5.3708 5.9710 6.5348 7.0664 7.5692 8.0463 |
1.8 2.8008 3.7144 4.5548 5.0 6.0574 6.7350 7.3716 7.9718 8.5395 9.0780 |
3.1 4.2056 5.2149 6.1434 7.0031 7.8034 8.5520 9.2553 9.9183 10.5455 11.1405 |
1.3 2.5200 3.6337 4.6583 5.6068 6.4900 7.3160 8.0920 8.8237 9.5157 10.1723 |
|
x |
Варианты |
|||||
|
13 |
14 |
15 |
16 |
17 |
18 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
1.8 3.1057 4.2978 5.3944 6.4097 7.3549 8.2390 9.0696 9.8527 10.5934 11.2961 |
2.5 2.9003 3.2658 3.6019 3.9132 4.2030 4.4740 4.7286 4.9687 5.1958 5.4112 |
8.2 8.7528 9.2575 9.7217 10.1515 10.5517 10.9260 11.2776 11.6092 11.9228 12.2203 |
1.9 2.5481 3.1398 3.6841 4.1880 4.6572 5.0960 5.5083 5.8969 6.2646 6.6134 |
1.7 2.3767 2.9945 3.5628 4.0890 4.5788 5.0370 5.4675 5.8733 6.2572 6.6213 |
1.1 1.9387 2.7044 3.4088 4.0610 4.6681 5.2360 5.7695 6.2725 6.7483 7.1997 |
|
x |
Варианты |
|||||
|
19 |
20 |
21 |
22 |
23 |
24 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
2.3 3.1673 3.9591 4.6875 5.3619 5.9897 6.5770 7.1287 7.6489 8.1409 8.6076 |
7.8 8.2 8.1829 8.3510 8.5066 8.6515 8.7870 8.9143 9.0344 9.1479 9.2556 |
6.6 6.7144 6.8188 6.9148 7.0038 7.0866 7.1640 7.2368 7.3053 7.3702 7.4318 |
7.7 7.8239 7.9370 8.0411 8.1374 8.2271 8.3110 8.3898 8.4641 8.5344 8.6011 |
4.4 4.5334 4.6553 4.7673 4.8711 4.9677 5.0580 5.1429 5.9 5.2986 5.3704 |
5.5 5.6430 5.7735 5.8935 6.0047 6.1082 6.2050 6.2959 6.3817 6.4628 6.5397 |
|
x |
Варианты |
|||||
|
25 |
26 |
27 |
28 |
29 |
30 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
3.2 3.6861 4.1298 4.5381 4.9160 5.2679 5.5970 5.9062 6.1977 6.4735 6.7351 |
3.3 3.8051 4.2663 4.6905 5.0833 5.4490 5 7910 6.1123 6.4153 6.7018 6.9737 |
3.4 3.9051 4.3663 4.7905 5.1833 5.5490 5.8910 6.2123 6.5153 6.8018 7.0737 |
3.5 4.0242 4.5028 4.9430 5.3506 5.7301 6.0850 6.4185 6.7328 7.0302 7.3123 |
3.6 4.1337 4.6210 5.0692 5.4842 5.8706 6.2320 6.5715 6.8916 7.1944 7.4816 |
3.7 4.2433 4.7392 5.1955 5.6179 6.0112 6.3790 6.7246 7.0504 7.3586 7.6509 |
з6. Дробно-рациональная зависимость y = x/(a*x+b).
Проведема преобразования 
Обозначим Y =  , X =
, X =  , A = b, B = a.
, A = b, B = a.
Y = AX + B -а линейная зависимость относительно переменных X и Y.
Определим коэффициенты пользуясь, таблицей:
|
X |
|
|
Е |
|
|
Y |
|
|
Е |
|
После того как коэффициенты A и B найдены по методу наименьших квадратов, коэффициенты a и b находятся по формулам: a = B, b = A.
Варианты заданий
Используя таблицу, определить параметры по способу наименьших квадратов. Найти эмпирическую функцию ва виде:
y = x/(a*x+b).
|
x |
Варианты |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
0.0813 0.0863 0.0909 0.0952 0.0993 0.1031 0.1067 0.1100 0.1132 0.1162 0.1190 |
0.2381 0.2552 0.2715 0.2870 0.3017 0.3158 0.3292 0.3421 0.3543 0.3661 0.3774 |
0.6 0.6509 0.7595 0.8844 1.0294 1.2 1.4035 1.6505 1.9565 2.3457 2.8571 |
0.1695 0.1937 0.2198 0.2481 0.2789 0.3125 0.3493 0.3899 0.4348 0.4847 0.5405 |
0.5 0.4120 0.3593 0.3242 0.2991 0.2804 0.2658 0.2541 0.2446 0.2366 0.2299 |
0.1220 0.1394 0.1583 0.1788 0.2011 0.2256 0.2524 0.2819 0.3147 0.3512 0.3922 |
|
x |
Варианты |
|||||
|
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
-0.0820 -0.0865 -0.0908 -0.0947 -0.0983 -0.1017 -0.1048 -0.1078 -0.1106 -0.1132 -0.1156 |
0.1190 0.1218 0.1242 0.1263 0.1282 0.1299 0.1314 0.1327 0.1339 0.1350 0.1361 |
0.1370 0.1425 0.1474 0.1519 0.1559 0.1596 0.1629 0.1660 0.1689 0.1715 0.1739 |
-0.3846 -0.4641 -0.5607 -0.6806 -0.8 -1.0345 -1.3115 -1.7172 -2.3684 -3.5849 -6.7 |
-0.1563 -0.1812 -0.2091 -0.2403 -0.2756 -0.3158 -0.3620 -0.4156 -0.4787 -0.5539 -0.6452 |
-0.2128 -0.2651 -0. -0.4262 -0.5600 -0.7692 -1.1429 -2. -6. 7.6 2.5 |
|
x |
Варианты |
|||||
|
13 |
14 |
15 |
16 |
17 |
18 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
0.0709 0.0768 0.0825 0.0881 0.0935 0.0987 0.1038 0.1087 0.1135 0.1182 0.1227 |
0.1724 0.2128 0.2643 0.3325 0.4268 0.5660 0.7921 1.2230 2.3684 14.6154 -4. |
0.1 0.1076 0.1149 0.1220 0.1287 0.1351 0.1413 0.1473 0.1531 0.1586 0.1639 |
-0.5 -0.4762 -0.4580 -0.4437 -0.4321 -0.4225 -0.4145 -0.4077 -0.4018 -0.3967 -0.3922 |
0.0763 0.0816 0.0866 0.0913 0.0958 0.1 0.1040 0.1079 0.5 0.1150 0.1183 |
-0.4762 -0.3198 -0.2510 -0.2124 -0.1877 -0.1705 -0.1578 -0.1481 -0.1404 -0.1342 -0.1290 |
|
x |
Варианты |
|||||
|
19 |
20 |
21 |
22 |
23 |
24 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
-0.0893 -0.1010 -0.1134 -0.1266 -0.1406 -0.1554 -0.1713 -0.1883 -0.2064 -0.2259 -0.2469 |
0.0870 0.1015 0.1179 0.1366 0.1580 0.1829 0.2122 0.2471 0.2894 0.3417 0.4082 |
0.0407 0.0437 0.0467 0.0495 0.0522 0.0548 0.0573 0.0598 0.0621 0.0643 0.0664 |
0.0847 0.0969 0.1101 0.1244 0.1400 0.1571 0.1758 0.1965 0.2195 0.2452 0.2740 |
0.0493 0.0534 0.0574 0.0612 0.0650 0.0686 0.0722 0.0757 0.0790 0.0823 0.0855 |
0.1190 0.1408 0.1662 0.1961 0.2318 0.2752 0.3292 0.3981 0.4891 0.6149 0.8 |
|
x |
Варианты |
|||||
|
25 |
26 |
27 |
28 |
29 |
30 |
|
|
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
0.0909 0.1053 0.1212 0.1390 0.1591 0.1818 0.2078 0.2378 0.2727 0.3140 0.3636 |
0.1961 0.2941 0.5042 1.2745 -4.1176 -0.8824 -0.5229 -0.3846 -0.3114 -0.2661 -0.2353 |
-0.1471 -0.1412 -0.1367 -0.1331 -0.1301 -0.1277 -0.1256 -0.1238 -0.1223 -0.1209 -0.1198 |
-1.2500 -1.6418 -2. -3.1707 -5. -10. -80. 15.4545 7.5 5.1351 4. |
-0.4167 -0.5263 -0.6742 -0.8844 -1.2069 -1.7647 -2.9630 -7.3913 22.5 4.8718 2.8571 |
0. 0.2799 0.2469 0.2245 0.2083 0.1961 0.1865 0.1788 0.1724 0.1671 0.1626 |
Вопросы для самопроверки
1.
2. В чем суть приближения заданной функции по методу наименьших квадратов?
3.
4. Можно ли при аппроксимации полиномом таблично заданной функции обеспечить прохождение аппроксимирующей функции точно через все точки?
5. Назначение весовых коэффициентов в критерии близости исходной и аппроксимирующей функций.
6. Можно ли повысить точность, одновременно величив в несколько раз все весовые коэффициенты?
7. Всегда ли величение суммы квадратов отклонений соответствует худшей близости исходной и аппроксимирующей функций?
8. Можно ли с помощью МНК найти параметры не полиномиальной аппроксимирующей функции?
9. В чем отличие применения метода при использовании в качестве аппроксимирующей функции полинома и показательной функции?
10. В каком случае система нормальных уравнений получается линейной относительно искомых коэффициентов?
11. В каком случае не дастся получить искомые коэффициенты непосредственно из решения системы нормальных уравнений?
12. Можно ли обеспечить требование, чтобы аппроксимирующая функция практически точно проходила через отдельные выбранные точки?
13. В чем основное достоинство квадратичного критерия близости исходной и аппроксимирующей функций?
Ответы:
Метод наименьших квадратов
4. Вообще говоря, можно, если задать степень аппроксимирующего полинома равной номеру последней точки (если нумерация точек идет от нуля). Однако в этом случае аппроксимирующая функция превращается в интерполяционную.
5. Весовые коэффициенты в критерии близости исходной и аппроксимирующей функций показывают относительную важность "вклада" точки в общую сумму квадратов отклонений (в случае квадратичного критерия). Варьируя их, можно повысить точность аппроксимации в отдельных точках, как правило, в наиболее важных в конкретной задаче.
6. Нельзя все весовые коэффициенты для повышения точности величить одновременно в одинаковое число раз, так как при этом не изменится их отношение и не изменится относительная важность отдельных точек.
7. Нет, не всегда величение суммы квадратов отклонений соответствует худшей близости исходной и аппроксимирующей функций. Например, при введении отличных от единицы весовых коэффициентов (например, всех одинаковых) критерий увеличится за счет коэффициентов, не за счет величения отклонений.
8. Можно найти параметры в принципе любой аппроксимирующей функции.
9. При использовании в качестве аппроксимирующей функции, в которую искомые параметры входят нелинейно, система нормальных равнений получится также нелинейной, и ее не всегда возможно решить аналитически, поэтому приходится применять поисковые методы для нахождения минимума квадратичной меры близости.
10. Система нормальных равнений получается линейной только в случае, когда при квадратичной мере близости параметры в аппроксимирующую функцию входят линейно (например, в случае полиномиальных функций).
11.В том случае, когда система уравнений сильно не линейна, тогда лучше непосредственно искать минимум меры близости поисковыми методами (т.е. методами поиска оптимума), хотя можно попытаться решать эту нелинейную систему предназначенными для этого методами.
12.Практически можно: для этого достаточно задать в этих точках очень высокие весовые коэффициенты, что приведет к точному прохождению аппроксимирующей функции через эти точки (число таких точек не должно быть большим по сравнению с общим числом точек).
13. Квадратичный критерий близости исходной и аппроксимирующей функций является дифференцируемой функцией, что делает возможным использование необходимых условий минимума для определения параметров аппроксимирующей функции; в случае линейности аппроксимирующей функции от искомых параметров квадратичный критерий близости имеет единственный экстремум, и притом обязательно минимум.
Глава 10. Приближенные методы решения дифференциальных равнений с частными производными.
Многие задачи механики и физики приводят к исследованию дифференциальных уравнений с частными производными второго порядка. Так, например, при изучении различных видов волн - пругих, звуковых, электромагнитных, также других колебательных явлений мы приходим к волновому равнению
 |
где с - скорость распространения волны в данной среде.
 |
Процессы распространения тепл в однородном изотропном теле, так же как и явления диффузии, описываются уравнением теплопроводности
При рассмотрении становившегося теплового состояния в однородном изотропном теле мы приходим к равнению Пуассона
 |
При отсутствии источников тепла внутри тела равнение ( 3 ) переходит в уравнение Лапласа
 |
Уравнения ( 1 ) - ( 4 )а часто называют основными равнениями математической физики. Их подробное изучение дает возможность построить теорию широкого круга физических явлений и решить ряд физических и технических задач.
Каждое из равнений ( 1 ) - ( 4 ) имеет бесчисленное множество частных решений. При решении конкретной физической задачи, необходимо из всех этих решений выбрать то, которое довлетворяет некоторым дополнительным словиям, вытекающим из её физического смысла. Такими дополнительными словиями чаще всего являются так называемые граничные словия, т.е. словия, заданные на границе рассматриваемой среды, и начальные словия, относящиеся к одному какому-нибудь моменту времени, с которого начинается изучение данного физического явления. Совокупность начальных и граничных словий называется краевыми словиями.
Одним из методов решения дифференциальных равнений в частных производных является метод сеток. Идея метода заключается в следующем. Для простоты, ограничимся случаем только функции двух переменных, и будем полагать, что решение равнения ищется на квадратной области единичного размера. Разобьем область сеткой. Шаг сетки по оси x и по оси y, вообще говоря, может быть разный. По определению частная производная равна

Если рассматривать функцию только в злах сетки, то частную производную можно записать в форме

где зел 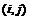 асоответствует точке
асоответствует точке  правой конечной разностью.
Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.
правой конечной разностью.
Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.
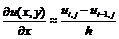
Такое выражение называется левой конечной разностью. Можно получить центральную конечную разность, найдя среднее этих выражений.
Теперь получим выражения для вторых производных.

В данном случае для нахождения производной мы использовали симметричные точки. Однако, очевидно, можно было бы использовать точки с несимметричным расположением.
10.1. равнения гиперболического типа
В качестве примера рассмотрим решение волнового равнения (уравнения гиперболического типа).

Уравнение будем решать методом сеток. Запишем равнение в конечных разностях

Полученное равнение позволяет выразить значение функции u в момент времени 
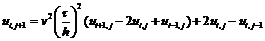
Такая разностная схема называется явной, так как искомая величина получается в явном виде. Она устойчива, если
Зададим начальные словия: смещение струны U в начальный и последующий моменты времени описывается синусоидальной функцией.

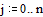
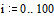

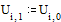
(Совпадение смещений при j=0 и j=1 соответствует нулевой начальной скорости.)
Зададим граничные словия: на концах струны смещение равно 0 в любой момент времени 

Будем полагать коэффициент 



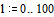
Записываем равнение в конечных разностях, разрешенное относительно 

Представляем результат на графике

10.2. равнения параболического типа.
Еще один пример использования конечных разностейЦ равнение диффузии.

Это равнение параболического типа. Явная разностная схема для этого равнения имеет вид
 аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.3)
аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.3)
Эта разностная схема стойчива, если 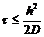
Задаем коэффициента  а
а
и диапазон изменения пространственной и временной координат:
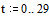
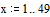
Задаем начальные и граничные словия


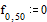

Уравнение в конечных разностях имеет вид
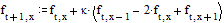
Представляем результаты на графике. (Для большей наглядности изображена только центральная часть)


Основное достоинство явных методовЦ их простотЦ зачастую сводится на нет достаточно жесткими ограничениями на величину шага. Явные схемы обычно стойчивы при столь малых шагах по времени, что они становятся непригодными для практических расчетов. Этого существенного недостатка позволяют избежать неявные схемы. Свое название они получили потому, что значения искомой функции на очередном временном шаге не могут быть явно выражены через значения функции на предыдущем шаге.
Рассмотрим применение неявной схемы на примере равнения теплопроводности
 а аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.4)
а аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.4)
Запишем неявную разностную схему для этого равнения
 MACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.5)
MACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.5)
Здесь первый индекс соответствует пространственной, а второйЦ временной координате. В отличие от явной схемы, для вычисления в правой части равнения используются значения функции на том же самом временном шаге.
Вводя обозначение  аGOTOBUTTON
ZEqnNum485383а \* MERGEFORMAT (5.5)
аGOTOBUTTON
ZEqnNum485383а \* MERGEFORMAT (5.5)
 аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.6)
аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.6)
или в матричной форме
 аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.7)
аMACROBUTTON MTPlaceRef \* MERGEFORMAT аSEQ MTEqn \h \* MERGEFORMAT (5.7)
где 
Задаем количество злов сетки (в данном случае оно одинаково для обеих переменных) 

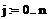

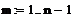
Задаем значения параметров 


и начальное распределение температуры в области

Формируем матрицы равнения аGOTOBUTTON ZEqnNum743242а \* MERGEFORMAT (5.7)


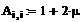


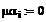


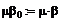
Находим решение системы 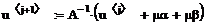

Лабораторная работа № 28.
Уравнений Лапласа и Пуассона
Варианты заданий.
Найти решение u(x,y) задачи Дирихле в квадрате со стороной 1 для равнения Лапласа с краевыми словиями вида u(0,y) = f1(y), u(1,y) = f2(y), u(x,0) = f3(x), u(x,1) = f4(x).
|
N варианта |
f1(y) |
f2(y) |
f3(x) |
f4(x) |
|
1 |
y2 |
cosy+(2-cos1)y |
x3 |
x+1 |
|
2 |
ey-ey2 |
y |
-x3+1 |
x2 |
|
3 |
y2+1 |
y |
sinx+1-x |
-x3(1+sin1) |
|
4 |
0 |
y |
sinx-x3sin1 |
X |
|
5 |
ey+y2(1-e)-1 |
y |
0 |
x |
|
6 |
y2 |
cosy+y(3-cos1) |
x3 |
2x+1 |
|
7 |
0 |
y |
sinx-x3sin1 |
x2 |
|
8 |
2e-(1+2e)y2-1 |
-y |
-x3+1 |
x-2 |
|
9 |
-10y2-8y+6 |
-10y2-30y+22 |
9x2+7x+6 |
9x2-15x-12 |
|
10 |
-7y2-5y+3 |
-7y2-21y+13 |
6x2+4x+3 |
6x2-12x-9 |
|
11 |
-6y2-4y+2 |
-6y2-18y+10 |
5x2+3x+2 |
5x2-11x-8 |
|
12 |
-5y2-3y+1 |
-5y2-15y+7 |
4x2+2x+1 |
4x2-24x-21 |
|
13 |
-19y2-17y+15 |
-19y2-57y+49 |
18x2+16x+15 |
48x2-24x-21 |
|
14 |
-2y-4y2 |
4-12y-4y2 |
x+3x2 |
-6-9x+3x2 |
|
15 |
1 |
y+1 |
1 |
x+1 |
|
16 |
1 |
y+1 |
1 |
x2+1 |
|
17 |
1 |
ey |
1 |
ex |
|
18 |
e2-y |
e2-y |
ex |
ex-1 |
|
19 |
-y3 |
1-y3 |
x2 |
x2-1 |
|
20 |
5y-y2 |
4+5y-y2 |
x2+3x |
x2+3x+4 |
|
21 |
3-7y |
7-6y |
4x+3 |
5x-4 |
|
22 |
5-8y |
11-7y |
6x+5 |
7x-3 |
|
23 |
y2+4y |
y2+4y+4 |
x2+3x |
x2+3x+5 |
|
24 |
y2 |
(1-y)2 |
x2 |
(x-1)2 |
|
25 |
y2 |
y2+2y |
x2-x |
x2+x+1 |
|
26 |
y |
y +e |
ex |
ex+1 |
|
27 |
0 |
tgy |
0 |
Tgx |
|
28 |
0 |
Siny |
0 |
Sinx |
|
29 |
-siny |
sin(1-y) |
sinx |
sin(x-1) |
|
30 |
1 |
1+cosy |
X |
x+cosx |
Пример выполнения задания.
Для решения равнений Пуассона  аи Лапласа (частный случай, когда
аи Лапласа (частный случай, когда 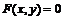 relax(a,
b, c, d, e, f, u, rjac), реализующая метод релаксации. Фактически, эту функцию можно использовать для решения эллиптического равнения общего вида
relax(a,
b, c, d, e, f, u, rjac), реализующая метод релаксации. Фактически, эту функцию можно использовать для решения эллиптического равнения общего вида
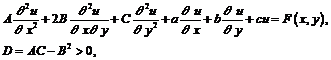
которое может быть сведено к равнению в конечных разностях

В частности, для равнения Пуассона коэффициенты 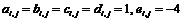
Идея метода релаксации заключается в следующем. Если нет источников
(уравнение Лапласа), то значение функции в данном зле на текущем шаге  аопределяется как среднее значение функции в ближайших злах на предыдущем шаге k
аопределяется как среднее значение функции в ближайших злах на предыдущем шаге k

При наличии источников разностная схема имеет вид 
Метод релаксации сходится достаточно медленно, так как фактически он использует разностную схему аGOTOBUTTON ZEqnNum854194а \* MERGEFORMAT (5.3) с максимально возможным для двумерного случая шагом 
В методе релаксации необходимо задать начальное приближение, то есть значения функции во всех злах области, так же граничные словия.
Функция relax возвращает квадратную матрицу, в которой:
1) расположение элемента в матрице соответствует его положению внутри квадратной области,
2) это значение приближает решение в этой точке.
Эта функция использует метод релаксации для приближения к решению.
Вы должны использовать функцию relax, если Вы знаете значения искомой функции u(x, y) на всех четырех сторонах квадратной области.
ргументы:
a, b, c, d, eЦ квадратные матрицы одного и того же размера, содержащие коэффициенты дифференциального равнения.
fЦ квадратная матрица, содержащая значения правой части равнения в каждой точке внутри квадрата
uЦ квадратная матрица, содержащая граничные значения функции на краях области, также начальное приближение решения во внутренних точках области.
rjacЦ Параметр, управляющий сходимостью процесса релаксации. Он может быть в диапазоне от 0 до 1, но оптимальное значение зависит от деталей задачи.
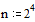
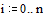
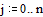
Задаем правую часть равнения Пуассона - два точечных источника
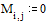

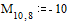
Задаем значения параметров функции relax
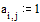

 а
а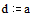 а
а 
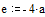
Задаем граничные словия и начальное приближение Ц нули во всех внутренних точках области
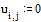 а
а 
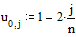


Находим решение 
и представляем его графически в виде поверхности и линий ровней.


Если граничные словия равны нулю на всех четырех сторонах квадрата, можно использовать функцию multigrid.

10.3. Телеграфное равнение.
Пусть i(x, t) -Ч сила тока в проводе в точке с абсциссой х в момент времени t, a v(x, t) Чнапряжение в той же точке в тот же момент времени. Тогда, применяя закон Ома к малому частку провода (х, х+Dх), получим
v(x, t) - v(x + Dx, t)=i(x, t)*RDx +  Dx.
Dx.
В левой части этого равенства стоит падение напряжения на участке (х, х+Dх), а в правой - сумма электродвижущих сил: электродвижущая сила, обусловленная омическим сопротивлением (она равна произведению силы тока i(x, t) на сопротивление данного частка провода RDx), и электродвижущая сила, обусловленная самоиндукцией. После деления обеих частей этого равенства на Dх и перехода к пределу при Dх о0 получим
- (x, f)=R*i(x, t) + L*
(x, f)=R*i(x, t) + L* (x, t) (1)
(x, t) (1)
Мы получили одно дифференциальное равнение, связывающее неизвестные функции i(x, t) и v(x, t). Составим теперь второе равнение, связывающее те же функции. Для этого чтем, что все количество электричества, притекающее на элементарный часток (х, х+Dх) за время Dt, равно сумме следующих величин:
) количества электричества, необходимого для зарядки этого элемента; оно равно емкости С*Dха этого частка провода, множенной на прирост напряжения на этом частке за время, протекшее с момента t до момента t+Dt;
б) количества электричества, необходимого для компенсации потерь, происходящих из-за несовершенства изоляции; это количество электричества равно течке на данном участке за время Dt (т. е. GDxDt), множенной на напряжение в момент t в данной точке провода.
Итак,
[i (х, t)-i(x + D х, t)] Dt = CDx*[v(x, t+D t) -v(x, t)] + G*Dx*Dt*v(x, t).
Деля все члены этого равенства на Dх*Dt и переходя к пределу при D х о 0, D t о 0, получим
- (х, t)=C*
(х, t)=C* x, t) + G* v(x, t) (2)
x, t) + G* v(x, t) (2)
Уравнения (1) и (2) образуют систему равнений с неизвестными функциями i(x, t) и v(x, t). Исключив из этой системы равнений функцию v(x, t), мы получим одно равнение с одной неизвестной функцией i(x, t); это можно сделать следующим образом: продифференцируем обе части первого равнения по t, обе части второго Ч по х и сложим почленно эти равнения, предварительно множив первое на ЧС; тогда мы получим
- 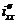 RC
RC а- LC
а- LC а+ G
а+ G
Подставляя теперь сюда  = ЧRiЧL
= ЧRiЧL аиз уравнения (1), получим окончательно
аиз уравнения (1), получим окончательно
 =LC
=LC а+ (RC
+ LG)
а+ (RC
+ LG)  а+ RGi (3)
а+ RGi (3)
Это и будет искомое равнение для определения функции i(x, t) - телеграфное уравнение для силы тока.
Заметим, что аналогичному равнению (и притом с теми же коэффициентами) довлетворяет и функция v (x, t); для того чтобы в этом бедиться, достаточно исключить i(x, t) из равнений (1) и (2):
 =LC
=LC а+ (RC
+ LG)
а+ (RC
+ LG)  а+ RGv (4)
а+ RGv (4)
(4)-лтелеграфное равнение для напряжения. Если R = 0, G=0 (т. е. если омическое сопротивление и течки столь малы, что ими можно пренебречь), то телеграфное равнение прощается; так, например, равнение для определения силы тока будет выглядеть следующим образом:
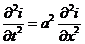
где а2= . Как мы видим, оно не отличается от равнения свободных поперечных колебаний струны или от равнения свободных продольных колебаний стержня (при словии малости колебаний).
. Как мы видим, оно не отличается от равнения свободных поперечных колебаний струны или от равнения свободных продольных колебаний стержня (при словии малости колебаний).
Уравнение (3), или совпадающее с ним равнение (4), называется телеграфным уравнение.
С помощью замены переменной w(x,
t)= i(x, t) в равнении (3) можно исключить член, содержащий первую производную:
i(x, t) в равнении (3) можно исключить член, содержащий первую производную:
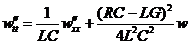 (5)
(5)
налогично можно простить и равнение (4).
Если, в частности, RCЧLG=0 (в этом случае говорят, что линия свободна от искажений), то равнение (5) сводится к следующему:
Начальные словия. Обычно в качестве начальных словий в телеграфном равнении задаются сила тока и напряжение в цепи в начальный момент t=0:
i(x, 0) = j(х), v(x, 0)=y(x)
Отсюда легко найти начальные словия, например, для функции i(x, t):
I(x, 0) = j(х),  (x,0)= -
(x,0)= - j
(x).
j
(x).
Второе из этих словий получается, если использовать уравнение (1), подставив в него t =0 и чтя, что vx'(x, 0) =y'(x).
Граничные словия рассмотрим, например, в применении к левому концу провода (x =0):
1) если левый конец провода заземлен, то в этом конце электродвижущая сила равна нулю: v(0, t)=0;
2) если левый конец провода изолирован, то в этом конце провода ток равен нулю: i(0, t)=0;
3) если к левому концу провода приложена электродвижущая сила E(t), то v(0, t)=E(t).
С помощью равнений (1) или (2) граничные условия, заданные для напряжения v(x, t), можно свести к граничным словиям для силы тока i(x, t) и обратно;
4)а в проводе, который столь длинен, что его можно практически считать бесконечным в обе стороны, граничные словия не задаются.
Задания
1. В тонком прямолинейном проводе омическое сопротивление, емкость, течка (проводимость изоляции) и самоиндукция, отнесенные к единице длины провода, постоянны и равны соответственно R, С, G и L. Как задать начальные и граничные словия для разыскания силы тока i(x, t), если провод имеет конечную длину l, причем левый конец провода (x=0) заземлен, к правому концу (x =l) приложена электродвижущая сила E(t)? В начальный момент t=0 сила тока равнялась j(x), напряжение было равно y(х).
2. Как задать начальные словия в телеграфном равнении для напряжения
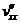 =LC
=LC а+ (RC
+ LG)
а+ (RC
+ LG)  а+ RGv
а+ RGv
если в начальный момент (t =0) сила тока и напряжение в цепи заданы равенствами
i(х, 0)=f(x), v(x, 0)=g(x)
3. Найти граничные словия, которые надо наложить на напряжение v(x, t), если известно, что к левому концу провода (x=0) приложена электродвижущая сила E(t), правый конец (х=l) изолирован.
4. Поставить краевую задачу для напряжения v(x, t) в проводе, расположенном на отрезке [0, l] оси абсцисс, если левый конец этого провода заземлен через сосредоточенное сопротивление R0, правый конец заземлен непосредственно.
Ответы
1. Одно начальное словие находится непосредственно из условий задачи:
i(x, 0) = j( x)
Для того чтобы найти второе начальное словие [то, которое надо наложить на  (x, t)], рассмотрим равнение (1),
найденное при решении предыдущей задачи:
(x, t)], рассмотрим равнение (1),
найденное при решении предыдущей задачи:
- (x, t) = Ri(x, t) + L
(x, t) = Ri(x, t) + L (x, t)
(x, t)
Полагая в этом равенстве t=0, получим
 (x, 0) = -
(x, 0) = -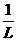
 (x, 0)-
(x, 0)- 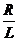 i(x, 0)
i(x, 0)
Так как, по словию задачи, v(x, 0) = y(x), то  (x, 0) =
(x, 0) =  x), так как, кроме того, i(x, 0) =j(x), то окончательно получаем
x), так как, кроме того, i(x, 0) =j(x), то окончательно получаем
 (x, 0) = -
(x, 0) = -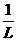
 x) -
x) - 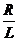 j(x, 0)
j(x, 0)
Это и будет вторым начальным словием.
Найдем граничные словия. Левый конец провода заземлен; это значит, что напряжение в левом конце провода равно нулю, т. е. v(0, t)=0. Но тогда и  t) =0.
Подставляя это в равенство (2) из предыдущей задачи при х=0, получим
t) =0.
Подставляя это в равенство (2) из предыдущей задачи при х=0, получим
 (0, t) =0
(0, t) =0
Это Ч граничное словие для функции i(x, t) на левом конце провода.
На правом конце провода, согласно словию задачи v(l, t)=E(t). Следовательно,  (l, t)=E'(t). Пользуясь снова формулой (2) из предыдущей задачи, найдем граничное словие для функции i(x, t) в точке х=1:
(l, t)=E'(t). Пользуясь снова формулой (2) из предыдущей задачи, найдем граничное словие для функции i(x, t) в точке х=1:
 ( l, t)=-C*E'(t)-G*E(t).
( l, t)=-C*E'(t)-G*E(t).
2. Первое начальное словие для напряжения задано: v (x, 0)=g(x). Применяя его для момента времени t=0, получим
- (x,0)= G v(x,0) + C
(x,0)= G v(x,0) + C (x,0).
(x,0).
Учитывая,
что v(x, 0)=g(x), i(x, 0)=f(x),  (x, 0)= f'(x) получим Чf'(x) = Gg(x)+C
(x, 0)= f'(x) получим Чf'(x) = Gg(x)+C (x, 0), откуда
(x, 0), откуда
 (x, 0)= -
(x, 0)= -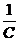 [f'(x) + Gg(x)].
[f'(x) + Gg(x)].
Это и есть второе начальное словие для функции v (x, t)
3. Первое граничное словие v(0, t)=E(t). Чтобы найти второе, чтем, что i(l, t) =0, отсюда  (l, t) =0. Из равнения (1)
при х= l получим
(l, t) =0. Из равнения (1)
при х= l получим
- l, t) = R i(l, t) + L
l, t) = R i(l, t) + L (l, t),
(l, t),
откуда
 l,t)=0;
l,t)=0;
это и есть второе граничное словие.
4. Разность потенциалов между землей (v =0) и левым концом провода (v = v(0, t)) равна произведению сосредоточенного сопротивления R0 на силу тока в левом конце i (0, t) поэтому
0- v(0, t)=R0*i(0, t) (1)
С другой стороны, из равнения (1) получаем при х=0:
- t)=Ri(0, t) + L
t)=Ri(0, t) + L (0, t),
(0, t),
Подставляя сюда из равенства (1)
i(0, t)= - аv (0, t),
аv (0, t),  t) = -
t) = - v (0, t),
v (0, t),
получим искомое граничное словие на левом, конце провода:
R0 t)=Rv(0, t) + L
t)=Rv(0, t) + L (0, t).
(0, t).
Граничное условие на правома конце провода таково: v(l,t)=0.
Глава 11. Тестовые задания.
з1. Тесты для проверки начального ровня знаний студента
1. В каком методе последовательные приближения вычисляются по формуле
1.
2.
3.
2. словие монотонной сходимости последовательных приближений в методе хорд является:
1.
2.
3.
3. Какова скорость сходимости метода касательных?
1. линейная
2. квадратичная
3. кубическая
4. Какова скорость сходимости метода хорд?
1. линейная
2. квадратичная
3. кубическая
5. Критерий сходимости итерационного метода:
1.
2.
3.
6. Формула Зейделя - это каноническая формула метода:
1. простых итераций
2. Зейделя
3. релаксации
7. Метод релаксации сходится, если:
1.
2.
3.
8. Число обусловленности матрицы системы влияет на:
1.
2.
3. выбор начального приближения
9. С помощью степенного метода находится:
1.
2.
3.
10. С помощью метода вращений:
1.
2.
3. матрица транспонируется
з2. Тестовые задания (промежуточный контроль).
Вариант № 1
1. В каком варианте ответа отделены корни равнений?
0,25x2-l,2502x3 = 0
) (0,0.1) Б) (1.7,1.8) В) (1,1.2) Г) (0.1,0.2)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
х3-1,75х + 0,75 = 0, [-10,10]
) [0.25,4] Б)[5.75, 10] В) [-10, -5.75] Г) [-2.5,0]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд?
0,25x2 - 1,2502x3 = 0, [-1.5,2]
) - 0,285 Б) 1,576 В) -0,233 Г) - 1,001
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона?
Х3-1.75х + 0,75 = 0, [-10,10]
) 1,827 Б) 4,1830 В) - 3.1250 Г) 5.2431
5. Чему равно третье приближение корня при решении следующего равнения методом итераций?
5х-х4-1 = 0, х0 = 1
A) 2.4 Б) 0.2 В) 3.6 Г) 5,1
Вариант № 2
1. В каком варианте ответа отделены корни равнений?
5х - х4-1 = 0
) (0.2,0.3) Б)(-1, - 0.9) В) (0.8,0.9) Г) (0.4,0.5)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
х4-18х2+6х-5 = 0, [-1.5, 2]
) [1.25,3] Б) [2.5,4.5] В) [1, 2.75] Г) [4, 4.5]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд?
0,25х2- 1,2502х3 = 0, [-1.5, 2]
) -0,285 Б)1,576 В) -0,233 Г) -1,001
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона?
х3-х-1-0, [1, 4.5]
) -8 Б) -10 В) -3 Г) -1
5. Чему равно третье приближение корня при решении следующего равнения методом итерация?
5х-  0 = 3
0 = 3
) 2.74 Б) 1.55 В) 3.48 Г)а 1.22
Вариант № 3
1. В каком варианте ответа отделены корни равнений?
0,25х3 + х-1,2502 = 0
) а[0, 0.1] Б)а [1.6, 1.8] В) [1, 1.1] Г) [0.2, 0.4]
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного уравнения?
0,25х3 + х-1,2502 = 0, [1.4,1.5]
) [1, 1.4375] Б)а [1, 3.520] В)а [1, 4.35] Г) [1, 2.575]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд
0,25х3 + х-1,2502 = 0, [0.5, 2]
) 0,8108 Б) 0,9744 В) 0,9967 Г) 0,5501
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона?
Х4-18х2 + 6х-5 = 0, [1, 5]
) 2,3480 Б) 0,1879 В) 1.1541 Г) 5,1370
5. Чему равно третье приближение корня при решении следующего равнения методом итерация?
5х -  0 = 3
0 = 3
) 2,74 Б)а 1,55 В) 3,48 Г) 1,22
Вариант № 4
1. В каком варианте ответа отделены корни равнений ?
5х - 
) (2.7, 2.8) Б) (2.1, 2.3) В)а (1.5, 1.7) Г)а (1.2,1.3)
2. Какой интервал выходит на 3-м шаге метода половинного деления
х3 + 2х - 7.8 = 0, [0,3]
) [0, 1.875] Б) [1.5, 1.875] В) [1.5, 2.75] Г) [0.1, 0.125]
З. Чему равно второе приближение корня при решении следующего равнения методом хорд ?
X + 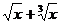 а=0, [0.1,1]
а=0, [0.1,1]
) 0.7378 Б) 0.2481а В) 0,8519 Г) 0,1532
4.Чему равно третье приближение корня при решении следующего уравнения методом Ньютона?
х3 + 2х - 7,8 = 0, [0,3]
А) 0,1569 Б) 2,5373 В) 4,1980 Г) 8,5791
5. Чему равно третье приближение корня при решении следующего равнения методом итерация ?
х -  0 = 0
0 = 0
) 2,32 Б) 1,29 В) 11,47 Г) 2,96
Вариант № 5
1. В каком варианте ответа отделены корни уравнений?
Х + 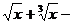
) (0.1, 0.2) Б) (0.7, 0.8) В) (1.5, 1.6) Г) (1.7, 1.8)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения ?
х3 + 2х-7,8 = 0 [0, 3]
) [1, 0.75] Б) [1.875, 1.9] В) [1.5, 1.875] Г) [0, 1.5]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд
Х + 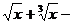
) 0,7876 Б) 0,8481 В) 0,7378 Г) 0,7577
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона?
х4- х- 1 = 0, [1,5]
) -0,7312 Б) 1,2751 В) 1,735 Г) 10,236
5. Чему равно третье приближение корня при решении следующего равнения методом итерации?
5х- х4-1 = 0, х0 =1
) 2,4 Б) 0,2 В) 3,6 Г) 5.1
Вариант № 6
1. В каком варианте ответа отделены корни равнений?
0,25х3 - 1,2502х3 = 0
) (0, 0.1) Б) (1.7, 1.8) В)(1, 1.2) Г) (0.1, 0.2)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3-1,75х + 0,75 = 0, [-10,10]
) [0.25, 4] B) [5.75, 10] В) [-10, -5.75] Г) [-2.5, 0]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд?
0,25х2 - 1,2502х3 = 0 [-1.5, 2]
) -0,285 Б) 1,576 В) -0,233 Г) -1,001
4. Чему равно третье приближение корня при решении следующего уравнения методом Ньютона?
Х3-1,75х + 0,75 = 0, [-10,10]
) 1,827 Б)а 4,1830 В) Ц3,1250 Г) 5,2431
5. Чему равно третье приближение корня при решении следующего равнения методом итерации ?
5х - х4 Ц 1 = 0, х0=1
) 2,4 Б) 0,2 В) 3,6 Г) 5,1
Вариант № 7
1. В каком варианте ответа отделены корни равнений?
5х - х4-1 = 0
) (0.2, 0.3) Б)(-1, -0.9) В) (0.8, 0.9) Г) (0.4, 0.5)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
х4-18х2 + 6х-5 = 0, [-1.5, 2]
A) [1.25, 3] Б) [2.5, 4.5] В) [1, 2.75] Г) [4, 4.5]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд?
0,25x2 Ц 1.2502x3 = 0, [-1.5, 2]
) -0,285 Б) 1,576 В) -0,233 Г) -1,001
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона?
X3- x - l = 0, [1, 4.5]
) -8 Б) -10 В) -3 Г) -1
5. Чему равно третье приближение корня при решении следующего равнения методом итерации?
5х-  0 = 3
0 = 3
) 2,74 Б) 1,55 В) 3,48 Г) 1,22
Вариант № 8
1. В каком варианте ответа отделены корни равнений?
0,25x3 + x Ц l.2502 = 0
) (0, 0.1) Б) (1.6,1.8) В) (1, 1.1) Г) (0.2, 0.4)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного уравнения?
0,25х3- х - 1,2502 = 0, [1.4, 1.5]
) [1, 1.4375] Б) [1, 3.520] В) [1, 4.35] Г) [1, 2.575]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд?
0,25х3+ х -1,2502=0, [0.5, 2]
) 0,8108 Б) 0,9744 В) 0,9967 Г) 0, 5501
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона
Х4 - 18х2 + 6х - 5 = 0, [1, 5]
) 2,3480 Б) 0,1879 В) 1,1541 Г) 5,1370
5. Чему равно третье приближение корня при решении следующего равнения методом итерация?
5х -  а- 5 = 0, х0
= 0
а- 5 = 0, х0
= 0
) 2,74 Б)а 1,55 В) 3,48 Г) 1,22
Вариант № 9
1. В каком варианте ответа отделены корни равнений?
5х -  а- 5 = 0
а- 5 = 0
) (2.7, 2.8) Б) (2.1, 2.3) В) (1.5, 1.7) Г) (1.2, 1.3)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
X3+ 2x - 7.8 = 0, [0, 3]
) [0, 1.875] Б) [l.5, 1.875] В) [1.5, 2.75] Г) [0.1, 0.125]
3. Чему равно второе приближение корня при решении следующею равнения методом хорд?
х + 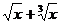 [0.1,
1]
[0.1,
1]
) 0,7378 Б) 0,2481 В)а 0,8519 Г) 0,1532
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона?
х3 + 2х - 7,8 = 0, [0, 3]
) 0,1569 Б) 2,5373 В) 4,1980 Г) 8,5791
5. Чему равно третье приближение корня при решении следующего равнения методом итерации?
х -  а- 2.5 = 0, Хо = 2
а- 2.5 = 0, Хо = 2
)а 2,32 Б) 1,29 В) 11,47 Г)а 2,96
Вариант № 10
1. В каком варианте ответа отделены корни уравнений?
Х + 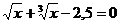
) (0.1, 0.2) Б) (0.7, 0.8) В) (1.5, 1.6) Г) (1.7, 1.8)
2. Какой интервал выходит на 3-м шаге метола половинного деления при решении данного равнения?
х3+ 2х -7,8 = 0, [0, 3]
A) [l, 0.75] Б) [1.875, 1.9] B) [1.5, 1.875] Г) [0, 1.5]
3. Чему равно второе приближение корня при решении следующего равнения методом хорд?
Х + 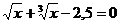 [0.1, 1]
[0.1, 1]
) 0,7876 Б) 0,8481 В) 0,7378 Г) 0,7577
4. Чему равно третье приближение корня при решении следующего равнения методом Ньютона?
х4- х Ц1 = 0, [1, 5]
) -0,7312 Б) 1,2751 В) 1,735 Г) 10,236
5. Чему равно третье приближение корня при решении следующего равнения методом итерации?
5х- х4 = 0, х0 = 1
) 2,4 Б) 0,2 В) 3,6 Г)а 5,1
з3. Тестовые задания (Зачет).
БИЛЕТ № 1
1. В каком из вариантов ответа отделены корни равнения?

. (0.1, 0.2) Б. (0.7, 0.8) В. (1.5, 1.6) Г. (1.7, 1.8)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 +2х Ц 7.8 = 0
. [1; 0.75], Б. [0.75; 1.5], В. [1.5; 1.875], Г. [0; 1.5],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
 а 0.1 ≤ х
≤ 1
а 0.1 ≤ х
≤ 1
. 0.7876 Б. 0.8481 В. 0.7378 Г. 0.7577
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
х4 - х Ц 1 =0, [1; 5],
. Ц0.7312 Б. 1.2751 В. 1.735 Г. 10.236
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X=1 по формуле Лагранжа.
. 16.18 Б. 17.02 В. 20.15 Г. 19.8
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X по формуле Ньютона.
. 16.8 Б. 17.02 В. 14.2 Г. 4.25
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 xy
xy
. 2.71 Б. 3.59 В. 0.141 Г. 5.19
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
5х - х4 Ц 1 = 0, х0 = 1
. 2.4 Б. 0.2 В. 3.6 Г. 5.1
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 2 + y + 1
2 + y + 1
. 5.242 Б. 0.128 В. 6.343 Г. 2.125
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 
. 1.25 Б. 10 В. 0.2 Г. 3.7
БИЛЕТ № 2
1. В каком из вариантов ответа отделены корни равнения?
0.25х3 + х - 1.2502 = 0
. (0, 0.1) Б. (1.6, 1.7) В. (1, 1.1) Г. (0.2, 0.4)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 -2х2 Ц 1.2 = 0
. [0.5; 1.25], Б. [0.5; 2 ], В. [-4; 2 ], Г. [-4; 0.75 ],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
5х -  Ц 5 =0, [1; 3],
Ц 5 =0, [1; 3],
. 1.2209 Б. 2.624 В. 1.590 Г. 4.6701
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
Х3 - 6х - 8 = 0, [2; 7]
. 12.4415 Б. -3.4351 В. -2.1 Г. 4.1530
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X=11 по формуле Лагранжа.
. 16.18 Б. 17.02 В. 20.15 Г. 19.8
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X=1.6 по формуле Ньютона.
. 13.026 Б. 20.011 В. 11.152 Г. 8.112
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 xy
xy
. 2.71 Б. 3.59 В. 0.141 Г. 5.19
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
х -  Ц 2.5 = 0, х0 = 2
Ц 2.5 = 0, х0 = 2
. 2.32 Б. 1.29 В. 11.47 Г. 2.96
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 3 + y + 1
3 + y + 1
. 6.343 Б. 10.808 В. 1.105 Г. 0.203
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 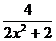
. 10.8 Б. 2.5 В. 1.6 Г. 8.1
БИЛЕТ № 3
1. В каком из вариантов ответа отделены корни равнения?
0.25х2 - 1.2502х3 = 0
. (0, 0.1) Б. (1.7, 1.8) В. (1, 1.2) Г. (0.1, 0.2)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 Ц 1.75х +0.75 = 0, [-10; 10],
. [2.75; 3.5], Б. [-2.5; 0], В. [-10; 2.75], Г. [3.5; 4.75],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
5х - х4 - 1 = 0, [0.5; 1],
. 0.3142 Б. 1.236 В. 0.200 Г. 1.
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
Х5 - х Ц 0.2 = 0, [-3; 2],
. Ц1.5672 Б. -2.1480 В. -3.1940 Г. 10.1020
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X=50 по формуле Лагранжа.
. 40.01а Б. 70.51 В. 201.35 Г. 100.11
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X=1.3 по формуле Ньютона.
. 1.2201 Б. 4.7790 В. 2.1136 Г. 6.3565
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?

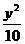
. 1.094 Б. 1.655 В. 2.15 Г. 8.11
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
0.25х2 Ц 1.2502х3 - 2 = 0, х0 = 1
. -7.803 Б. 0.620 В. 3.4 Г. -3.665
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 y2
y2
. -7.803 Б. 0.620 В. 3.4 Г.-3.665
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 
. 8.51 Б. 10.12 В. 2.06 Г. 1.11
БИЛЕТ № 4
1. В каком из вариантов ответа отделены корни равнения?
0.25х3 +х Ц1.2502 = 0
. (0, 0.1) Б. (1.6, 1.8) В. (1, 1.1) Г. (0.2, 0.4)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 +2х Ц 7.8 = 0
. [1.5; 2.525], Б. [1.5; 3 ], В. [1.5; 1.875 ], Г. [0; 1.875 ],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
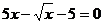 ≤ х ≤ 3
≤ х ≤ 3
. 2.624 Б. 1.2209 В. 3.1 Г. 4.6701
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
х4 - х Ц 1 =0, [1; 5],
. 1.2470 Б. 5.1420 В. Ц0.7312 Г. 11.2415
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X=55 по формуле Лагранжа.
. 211.15 Б. 91.15 В. 164.88 Г. 60.12
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X=1.6 по формуле Ньютона.
. 16.8 Б. 17.02 В. 14.2 Г. 4.25
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 xy
xy
. 2.44 Б. 7.15 В. 8.112 Г. 10.54
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
0.25х3 + х - 1.2502 = 0, х0 = 2
. 0.627 Б. 2.741 В. 1. Г. 3.520
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 3 + y + 1
3 + y + 1
. 6.343 Б. 2.818 В. 10. Г. 14.808
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 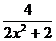
. 4.0 Б. 11.2 В. 2.5 Г. 10.8
БИЛЕТ № 5
1. В каком из вариантов ответа отделены корни равнения?
0.25х3 + х Ц1.2502 = 0
. (0, 0.1) Б. (1.6, 1.8) В. (1, 1.1) Г. (0.2, 0.4)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 - х Ц 1 = 0, [1; 4.5],
. [1; 1.4375], Б. [1; 3.520], В. [1; 4.35], Г. [1; 2.575],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
0.25х3 + х Ц1.2502 = 0, 0.5 ≤ х ≤ 2
. 0.8108 Б. 0.9744 В. 0.9967 Г. 0.5501
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
х4 - 18х2 Ц 6х - 5 =0, [1; 5],
. 2.3480 Б. 0.1879 В. 1.15641 Г. 5.1370
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X = 4 по формуле Лагранжа.
. 11.34 Б. 12.06 В. 19.98 Г. 13.73
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X = 3.2 по формуле Ньютона.
. 13.776 Б. 12.061 В. 19.981 Г. 13.73
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 xy2
xy2
. 18.64 Б. 10.18 В. 4.01 Г. 1.99
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
5х -  Ц 5 = 0, х0 = 3
Ц 5 = 0, х0 = 3
. 2.74 Б.1.55 В. 3.48 Г. 1.22
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 2 + 3y2
2 + 3y2
. 106.9 Б. 228.5 В. 10.1 Г. 50.7
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 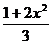
. 7.33 Б. 10.01 В. 1.22 Г. 4.18
БИЛЕТ № 6
1. В каком из вариантов ответа отделены корни равнения?
0.25х2 - 1.2502х2а = 0
. (0, 0.1) Б. (1.7, 1.8) В. (1, 1.2) Г. (0.1, 0.2)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 Ц 1.75х +0.75 = 0, [-10; 10],
. [0.25; 4], Б. [5.75; 10], В. [-10;-5.75], Г. [-2.5; 0],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
0.25х2 - 1.2502х2а = 0, -1.5 ≤ х ≤ 2
. Ц0.285 Б. 1.576 В. Ц0.233 Г. Ц1.001
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
Х3 Ц 1.75х + 0.75 =0, [-10; 10],
. 1.827 Б. 4.1830 В. Ц3.1250 Г. 5.2431
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X = 42 по формуле Лагранжа.
. 181.12 Б. 211.15 В. 90.15 Г. 150.1
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X = 3 по формуле Ньютона.
. 12.13 Б. 10.15 В. 13.25 Г. 11.50
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 x +
x +
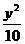
. 4.098 Б. 10.421 В. Ц5.112 Г. 1.655
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
5х - х4 Ц 1 = 0, х0 = 1
. 2.4 Б. 0.2 В. 3.6 Г. 5.1
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 2 y
2 y
. 1.6 Б. 2.5 В. 7.4 Г. 10.1
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 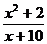
. 1.29 Б. 6.33 В. 8.22 Г. 20.21
БИЛЕТ № 7
1. В каком из вариантов ответа отделены корни равнения?
5х - х4 - 1 = 0
. (0.2, 0.3) Б. (-1, -0.9) В. (0.8, 0.9) Г. (0.4, 0.5)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 Ц 0.2х2 - 0.2х Ц1.2 = 0 [-4; 2],
. [1; 0.75], Б. [0.75; 1.5], В. [1.5; 1.875], Г. [0; 1.5],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
0.25х3 -+х - 1.2502 =0, 0.5 ≤ х ≤ 2
. 0.8108 Б. 0.9744 В. 0.9967 Г. 0.6501
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
Х3 Ц 0.2х2 - 0.2х - 1.2 = 0, [-4; 2],
. Ц1.8 Б. 2.1534 В. Ц3.2690 Г. 4.1571
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X = 40 по формуле Лагранжа.
. 38.14 Б. 40.45 В. 167.52 Г. 200.11
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X = 1 по формуле Ньютона.
. 10.11 Б. 4.25 В. 6.13 Г. 7.15
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 xy2
xy2
. 6.41 Б. 1.99 В. 11.15 Г. Ц3.11
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
5х -  Ц 5 = 0, х0 = 3
Ц 5 = 0, х0 = 3
. 2.74 Б. 1.55 В. 3.48 Г. 1.22
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 3 + y + 1
3 + y + 1
. 6.343 Б. 10.828 В. 14.025 Г. 19.611
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 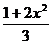
. 10.88 Б. 5..44 В. 1.22 Г. 7.33
БИЛЕТ № 8
1. В каком из вариантов ответа отделены корни равнения?
5
. (2.7, 2.8) Б. (2.1, 2.3) В. (1.5, 1.7) Г. (1.2, 1.3)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 +2х Ц 7.8 = 0 [0; 3],
. [0; 1875], Б. [1.5; 2.75 ], В. [1.5; 1.875 ], Г. [0.1; 0.125 ],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
 а 0.1 ≤ х
≤ 1
а 0.1 ≤ х
≤ 1
. 0.7378 Б. 0.2481 В. 0.8519 Г. 0.1532
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
Х3 + 2х - 7.8 = 0, [0; 3],
. 0.1569 Б. 2.5373 В. 4.1980 Г. 8.5791
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X = 4по формуле Лагранжа.
. 11.34 Б. 12.06 В. 16.98 Г. 13.73
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X = 3.7 по формуле Ньютона.
. 15.1085 Б. 11.245 В. 13.0045 Г. 12.1241
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 x2
+ y
x2
+ y
. 21.63 Б. 40.14 В. 32.13 Г. 1.01
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
х +  4 - 2.5 = 0,
х0 = 2
4 - 2.5 = 0,
х0 = 2
. 2.32 Б. 1.29 В. 11.47 Г. 2.96
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 y2
y2
. 5.242 Б. 0.128 В. 6.343 Г. 2.125
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 
. 15.4 Б. 119.199 В. 1.017 Г. 9.007
БИЛЕТ № 9
1. В каком из вариантов ответа отделены корни равнения?
0.25х3 + х - 1.2502 = 0
. (0.1, 0.2) Б. (1.6, 1.8) В. (1, 1.1) Г. (0.2,0.4)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 Ц6х Ц 8 = 0, [2; 7],
. [2; 2.537], Б. [3.535; 4.5 ], В. [2.625; 3.25 ], Г. [2.625; 4],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
0.25х3 + х - 1.2502 = 0, 0.5 ≤ х ≤ 2
. 0.9744 Б. 1.2502 В. 0.1417 Г. 0.4651
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
Х3 - 6х - 8 =0, [2; 7],
. 0.1792 Б. 3.1280 В. 1.2570 Г. -3.4351
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X = 11 по формуле Лагранжа.
. 16.18 Б. 17.02 В. 20.15 Г. 19.8
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X = 7.9 по формуле Ньютона.
. 40.311 Б. 55.125 В. 50.011 Г. 59.5305
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 x +
x +
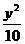
. 1.094 Б. 1.655 В. 2.152 Г. 6.875
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
5х - х4 Ц 1 = 0, х0 = 1
. 2.4 Б. 0.2 В. 3.6 Г. 5.1
9. Чему равно У3 при решении следующего дифференциального равнение; методом Эйлера, если У(0)= 1. Н= 0,5?
 2 + 3y2
2 + 3y2
. 228.5 Б. 116.9 В. 10.88 Г. 348.11
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 
. 4.20 Б. 2.06 В. 10.11 Г. 13.13
БИЛЕТ № 10
1. В каком из вариантов ответа отделены корни равнения?

. (0.1, 0.2) Б. (0.7, 0.8) В. (1.5, 1.6) Г. (1.7, 1.8)
2. Какой интервал выходит на 3-м шаге метода половинного деления при решении данного равнения?
Х3 - 3х2 +6х +3 = 0, [-3; 4],
. [2.25; 4.00], Б. [-3.2; 2.350], В. [-0.25; 1.735], Г. [-1.25; -0.375],
3. Чему равно второе приближение корня (Х2) при решении следующего равнения методом хорд (начальное приближение - Х0)
0.25х2 - 1.2502х3 = 0, -1.5 ≤ х ≤ 2
. Ц0.285 Б. 1.576 В. -0.233 Г. 1.475
4. Чему равно третье приближение корня (Х3) при решении следующего равнения методом Ньютоне (начальное приближение - Х0)?
Х3 - 3х2 + 6х +3 = 0, [-3; 4],
. 8.4420 Б. 2.1517 В. 1.2571 Г. 1-0.4
5. Для функции, заданной таблицей
|
X |
2 |
6 |
17 |
21. |
60 |
|
У |
11 |
15 |
23 |
35 |
67 |
Вычислить значение функции в точке X = 11 по формуле Лагранжа.
. 16.18 Б. 17.02 В. 20.15 Г. 19.8
6. Для функции, заданной таблицей
|
X |
2 |
4 |
6 |
8. |
|
У |
10 |
16 |
28 |
62 |
вычислить значение функции в точке X = 7 по формуле Ньютона.
. 39.11 Б. 22.41 В. 30.15 Г. 41.25
7. Чему равняется У2 при решении следующего дифференциальногоа уравнения методом Рунге-Кутта, если У(0) = 1, Н = 0,5?
 x +
x +
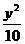
. 1.094 Б. 1.655 В. 2.152 Г. 6.875
8. Чему равно третье приближение корня (.Х3) при решении следующего ypaвнения методом итерации?
0.25х3 + х - 1.250 = 0, х0 = 2
. 0.627 Б. 2.741 В. 1. Г. 3.520
9. Чему равно У3 при решении следующего дифференциального равнение методом Эйлера, если У(0)= 1. Н= 0,5?
 y2
y2
. 2.818 Б. 1.441 В. 10.115 Г. 14.002
10. Задана подынтегральная функция y = f(x). Промежуток интегрирования: [0; 3 ], Н = 1. Чему равен интеграл при вычислении его методом трапеции.
Y = 
. 1.25 Б. 10 В. 0.2 Г. 3.7
з4. Тестовые вопросы.
1. а называется число, котороеЕ
) незначительно больше точного числа
Б) незначительно меньше точного числа
В) оба выражения верны.
2. Dа приближенного а называетсяЕ, где А -точное число.
) разность Dа = А- Б) Dа = А/ В) Dа = А*а
3. Пусть А- точное число, а- приближенное, Dа- абсолютная погрешность, то верная запись а) А = + D б) А = - D в) А = Dа
4. Относительной погрешностью h называется отношениеЕ
а) h = Dа/ çАï
б) h = D/А
в) h = D/а
г) h = Dа/а
5. Число 0.00701 содержитЕ значащих цифр.
А) 5 Б) 4 В) 3 Г) 2 Д) 1
6. n-первых значащих цифр приближенного числа являются верными, если абсолютная погрешность не превышаетЕ единиц разряда.
А) 1/2 Б) 1/3а В) 1/4 Г) 1/5
7. абсолютная погрешность суммы нескольких приближенных чисеЕабсолютныха погрешностей этих чисел.
а) больше или равно б) меньше в) равно г) меньше или равно
8. абсолютная погрешность разности 2-х приближенных чисел равнЕпогрешности двух приближенных чисел.
А) сумме Б) разности В) полу сумме.
9. Относительная погрешность произведения нескольких приближенных чисел отличных от нуля равнЕэтих приближенных чисел.
А) не превышает произведения Б)не превышает суммы В) не превышает разности
10. Относительная погрешность частногоЕотносительных погрешностей делимого и частного.
А) не превышает наибольшую иза Б) суммы погрешностей
12. Если непрерывная функция принимает значения f(x) принимает значения f(a)*f(b)<0 на концах [a,b], то внутри этого отрезка имеется
) один корень б) два корня в) три корня
13. если с - корень в методе дихотомии, то он находится по формулеЕ
)  б)
б) 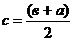 ав)
ав) 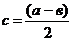
14. xn- корень равнения в методе хорд, то он находится по формулеЕ
)  б)
б) 
в)  г)
г) 
15. n - корень равнения в метод Ньютона ( касательных ), то он находится по формуле:
) 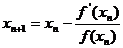 б)
б)  в)
в) 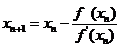 а
а
16. Процесс итерации хn= j(xn-1) сходится независимо от начального 
если a)  б)
б)  ав)
ав) 
17. Пусть в САу имеется 3 равнения и 3 неизвестных. При решении СЛАУ методом Гаусс сначала находятся корни в таком порядке Е
1) х1,х2,х3 2) х3, х2,х1 3) х1,х3,х2 а4) ах3,х1,х2
18. При решение СЛАУ методом итерации решение имеется, если сумм модулейа коэффициентова при неизвестных в правойа части, взятыха по строкамЕ
а)а большеа 1 б)а равноа 1 в)а меньшеа 1
19. таблица функций
|
х |
0,41 |
1,55 |
2,67 |
3,84 |
|
у(х) |
2,63 |
3,75 |
4,87 |
5,03 |
Найти значение функции в точкеа Х=1,91, пользуясь интерполяционныма многочленам Лагранжа
) 3,97а б) 4,15а в) 4,23 г) 4,43
20. Формула трапецийа для вычисления интеграла, имеет вид
) 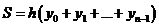
б) 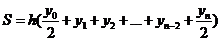
в) 
21. Формула прямоугольников, для вычисления интеграла имеет вид
) 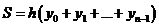
б) 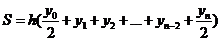
в) 
22. Формула Симпсона имеет вид
) 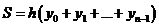
б) 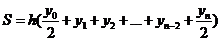
в) 
12. Список использованной литературы
1. Каган Б. М, Тер-Микаэлян Т. М. Решение инженерных задач на цифровых вычислительных машинах, М.ЧЛ-, Издательство. Энергия, 1964, 592 с. с черт.
2. Горинштейн А.М. Практика решения инженерных задач на ЭВМ.- М.: Радио и связь, 1984.-232с.
3. Применение ЭВМ в инженерных расчетах. - Всесоюзный заочный институт ж.д. транспорта. М:1986.
4. Петров А.В., Алексеев В.Е., Титов М.А. и др. Вычислительная техника в инженерных и экономических расчетах. - М.: Высшая школа, 1984.
5. Петров А.В., Алексеев В.Е., Титов М.А. и др. Вычислительная техника и программирование. - М.: Высшая школа, 1990. - 479с.
6. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1966, 664с.
7. Гутер Р.С, Резниковский П.Т. Вычислительная математика. Программная реализация вычислительных методов, Наука, 1971, -264с.
8. Амелькин В.В. Дифференциальные равнения в приложениях. - М. Наука, 1987. - 160стр.
9. Алексеев В.Е. и др. Вычислительная техника и программирование. Практикум по программированию. - Практическое пособие. М.: Высшая школа, 1991. - 400с.
10. Заварыкин В.М., Житомирский В.Г, Лапчик М.П. Численные методы, Просвещение, 1990, -176с.
11. Дьяконов В.Н. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ.- М. Наука. 1987. -240стр.
12. А.В. Копченова, К.А. Марон. Вычислительная математика в примерах и задачах.
13. Очков В.Ф. MathCad 7 PRO для студентов и инженеров. - М.: Компьютер Пресс, 1998. Ц384 с.
14. Алтухов Е.В, Рыбалко Л.А, Савченко В.С. - Основы информатики и вычислительной техники. - М.: Высшая школа, 1992,-303с.
15. Электротехника. Под ред. проф. В.Г.Герасимова, М, Высшая школа, 1985 г.
16. Борисов Ю. М. Липатов Д. Н. Общая электротехника, М., Энергоатомиздат, 1985г.
17. Бессонов Л. А. Теоретические основы электротехники, М., Высшая школа, 1978 г.
18. Сборник задач по электротехнике и основам электроники. Под ред. В. С. Пантюшина, М.Высшая школа, 1979г.
19. Электротехника и основы электроники. Методические казания и контрольные задания, М.Высшая школа, 1984г.
20. В. Д. Дьяконов. Справочник по расчетам на микрокалькуляторах, М. Наука 1986г.
21. А.С. Потапов, В.В. Кравец. Численные методы. учебное пособие для студентов физико-математического факультета - Воронеж: Изд-во ВГПУ, 1996. - 82 с.
22. Кацман Ю. Я. Прикладная математика. Численные методы. учебное пособие. - Томск: Изд. ТПУ, 2. - 68 с.
23. Пермский Государственный Технический ниверситет. РГР №1. Расчёт и исследование линейной электрической цепи с источниками постоянных воздействий- 2001г.
24. Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и ее применение. Издание 2-е, дополненное и переработанное. Издательство Солон-Р, Москва, 2001- 736с.
25. Гурский Д, Стрельченко Ю. Решение дифференциальных уравнений в Mathcad. Часть 1. Мир ПК, октябрь 2005г.
26. Дьяконов. В. П. Закон Мура и компьютерная математика. Exponenta Pro №1 (1) / 2003
27. Ю.Ю. Тарасевич Численные методы на Mathcadе - Астраханский гос. пед. н-т: Астрахань, 2.
28. Катаева Л.Ю. Вычислительная математика: Методическая разработка по курсу "Вычислительная математика" /РГОТУПС МПС РФ; Н. Новгород, 2003 с.
29. Очан Ю. С. Сборник задач по методам математической физики. Изд.2-е. учебное пособие для втузов. М., Высшая школа, 1973- 192с.
30. Васильков Ю.В, Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учеб. пособие. - М: Финансы и статистика, 1.-256с: ил.