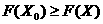Читайте данную работу прямо на сайте или скачайте
Разработка системы автоматического правления
Южно-Сахалинский институт экономики, права и информатики
Кафедра автоматизации
и энергетики
Курсовая работа
по дисциплине Теория автоматического правления (ТАУ)
тема: Разработка системы автоматического правления
Выполнил студент
группы А-41
Тесленко В.В.
Проверил
преподаватель
Стельмащук С.В.
Южно-Сахалинск
2005
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Разработка системы автоматического регулирования
В задании необходимо:
1) По данной структурной схеме определить передаточные функции по правляющему  аи возмущающему
аи возмущающему  авоздействию.
авоздействию.
2) Рассчитать графики переходных функций по правлению и по возмущению на программе PSM.
3) Рассчитать коэффициенты ошибки по положению и по скорости САР по правляющему воздействию.
4) Произвести D-разбиение по коэффициенту пропорциональности звена W1(p) и определить его граничное значение.
5) Оценить стойчивость САР по методу стойчивости в соответствии с вариантом.
6) Произвести синтез последовательного звена. При этом необходимо обеспечить следующие показатели качества процесса регулирования в скорректированной системе:
a) перерегулирование s £ 25 %;
b) время переходного процесса tпп £ 0.1 с;
c) точность скорректированной системы должна быть не ниже точности нескорректированной САР.
Вариант № 22
|
№ |
Структура |
W1 |
W2 |
W3 |
W4 |
Критерий устойчивости |
|
22 |
д |
|
|
|
|
Найквиста |
|
|
1. Определим передаточные функции по правляющему и возмущающему воздействию: 





Схема правляющего воздействия:

Схема возмущающего воздействия:

2. Графики переходных функций полученные при помощи программы PSM:
График переходной функции по управляющему воздействию:

График переходной функции по возмущающему воздействию:

3. Рассчитаем коэффициенты ошибок по положению и по скорости САР по правляющему воздействию:
Определим астатизм системы, рассмотрим Wраз(P):
 P/ Коэффициенты ошибки для данной системы:
P/ Коэффициенты ошибки для данной системы: 
C1 = ∞ - коэффициент ошибки по скорости.
4. Производим D-разбиение по коэффициенту пропорциональности звена W1(p) и определим его граничное значение Kгр.
Рассмотрим 
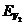
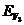
 .
.

Приравниваем знаменатель к нулю и решаем равнение: 


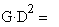 а=> ω1=0,
аили
а=> ω1=0,
аили

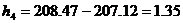

Подставим полученные корни в действительную часть:


Kгр=2,3844
5. Оценка стойчивости по критерию Найквитста.
С помощью графика построенного в программе MathCad 2001 Pro оцениваем стойчивость системы. На графике видно, что годограф не охватывает точку (-1;j0), следовательно система стойчива.

6. Произведем синтез последовательного звена:

Рассмотрим знаменатель 
0,2p4 + 0,2p3 + 0,05p2 + 0,4p3 + 0,4p2 + 0,1p + 2p3 + 2p2 + 0,5p + 4p2 + 4p + 1 + 5
0,2p4 + 2,6p3 + 6,45p2 + 4,6p + 6
В программе MathCad вводим функцию 
Из данных корней получаем функции, используя следующие формулы:



 а- коэффициент демпфирования
а- коэффициент демпфирования




Получаема 
Построим ЛАХ нескорректированной системы Lнск = L01(ω)
НЧ: 20lg5=20∙0,7=14а

Используя номограммы Солодовникова строим желаемую ЛАХ и определяем из заданных параметров (σтр=25%, tпп=0,1с) частоту среза ωс.
Pmax=1,5; Pmin = 1 - Pma x= 1 - 1,5 = -0,5
 ,
, 
По номограммам определяем L1 =1 0 и L2 = -10.
Строим ЛАХ регулятора:
Lр = Lж - Lнск
По полученной характеристике регулятора составляем равнение:
20lgk = 0а => k=1, lgω =
xа => ω=10x; 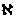

С помощью программы PSM составляем схему с регулятором м проверяем точность скорректированной системы.
Схема с регулятором:

Выходной сигнал схемы с регулятором: