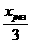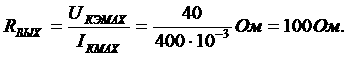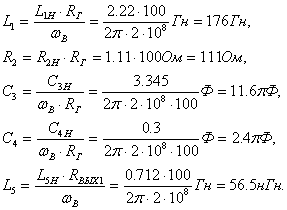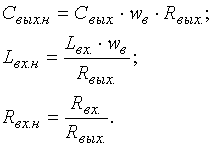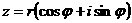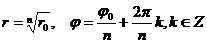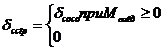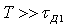Читайте данную работу прямо на сайте или скачайте
Расчет размерных цепей. Стандартизация
1.
Решить прямую задачу размерной цепи механизма толкателя, изображённого на рисунке 1.1., методами максимума-минимума и вероятностным. Способ решения стандартный,
3 = 100 мма






 |

Обозначения:а 1 Ц длина поршня;
2 - радиус поршня;
3 - расстояние между осями отверстий в
4 - расстояние от торца крышки до оси отверстия в ней;
5 - длина корпуса;
 - вылет поршня за пределы корпуса;
- вылет поршня за пределы корпуса;
Таблица 1.1.
|
1, мм |
2,мм |
3,мм |
4,мм |
5,мм |
|
|
%,риска |
|
|
20 |
100 |
110 |
153 |
|
0 |
1,0 |
iа
3 а
а

Таблиц
|
|
|
|
|
|
Коэффициент относительного рас-сеивания взятый в квадрате i )2 |
|
|
|
2.
2.1
2.1.1.
2.1.2.

 |
 |
||
а
i, Вi
 i
, BI
i
, BI
 |
 |
УВЕЛИЧИВАЮЩИЕ
2.1.3.
2.1.4.

2.1.5.
2.2.
2.2.1.
2.2.2.
2.2.1.1.
2.2.3.
 =а
=а
Где:
 - номинальный размер исходного звена;
- номинальный размер исходного звена;
 - номинальный размер составляющих звеньев;
- номинальный размер составляющих звеньев;
i а
2.2.4.
0D = i 0i,
i 0i,
 0i аа
0i аа
2.2.5.
2.2.5.1.
2.2.5.2.
tD
2.2.6.
2.3.
2.3.1.
Его принимают,
если несколько составляющих звеньев имеют один порядок и могут быть выполнены с примерно одинаковой точностью, т.е. :
1  0Dа
0Dа
 =
= 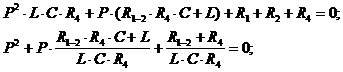 i
i =а D
=а D

Для метода iа
Для т/в метода: iа
Расчетное значение допусков округляют до стандартных по ГОСТ 6639-69, при этом выбирают стандартные поля допусков предпочтительного применения.
Если для метода D Способ равных допусков прост, но на него накладываются ограничения: номинальные размеры должны быть близки и технология обработки деталей должна быть примерно одинакова.
2.3.2.
Этот способ применяют, если все составляющие цепь размеры могут быть выполнены с допуском одного квалитета и допуски составляющих размеров зависят от их номинального значения.
Для теоретико-вероятностного метода:
Dа =а ср.
По словию задачи 1 D
D

сра =а
Для
Dа аср Приа
2.3.3.
ср  ср
ср 
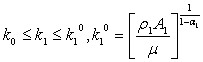
ср = 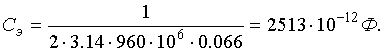
С чётом величины номинальных размеров и сложности их изготовления и ориентируясь на Тср назначаются допуски на все составляющие звенья по ГОСТ 6656 - 69.
При необходимости один из допусков корректируется.
Этот способ не имеет ограничений, но у него существует недостаток: он субъективный ( не подлежит автоматизации)
2.3.4.
1 и А2 ), то мы не можем применить способ равных допусков и способ одного квалитета. Мы буде применять стандартный способ.
2.5.
2.5.1.
 а
а
Метод учитывает только предельные отклонения звеньев размеров цепи и самые неблагоприятные их сочетания, обеспечивает заданную точность сборки бес подгонки деталей - полную взаимозаменяемость. Этот метод экономически целесообразен лишь для машин невысокой точности или для цепей, состоящих из малого числа звеньев.
2.5.2.
При допуске ничтожно малой вероятности несоблюдения предельных значений замыкающего размера, значительно расширяются допуски составляющих размеров и тем самым снижается себестоимость изготовления деталей.
 а
а

 а
а
iТ -
3.
3.1.
Dа
Определим, какие звенья увеличивающие, какие меньшающие. Для этого построим схему размерной цепи.
Приведем схему размерной цепи
a
Из рис. 3.2 следует, что 1,
А2, А3 а4,
А5а
x1а 2 а3 а4 = 5а
Подставляем в формулу
2.3.1
Dа =а 1а 2а 3Та 4а 5а
3.2.
D
ТD а
3.2.1.
3.2.1.1.
3.2.1.2.
Таблица 3.2.1.2. Сложность изготовления
Номинальный размер
Max
Min
A A A A A A A A
A
Максимальный допуска
Т T45 Т2 1а
3.2.1.3.
ТDа а
Допуски назначены верно.
3.2.2.
3.2.2.1.
Тсра
t 3.2.2.2.
Т T
3.3.
D
D
Чаще всего для наружных размерова
3.3.1.
Проверк
3.3.2.
Проверк
3.4.
3.4.1.
3.4.2.
3.5.
Максимума-минимума
Теоретико-вероятностный
1
160 +0,01
160 +0,02
2
28 +0,01
28
3
100 +0,05
100 +0,1
4
125 Ц0,025
125+0,04
5
135 Ц0,025
135-0,04
4.




 Dа
Dа

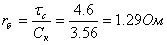




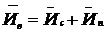



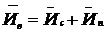


 4
4