Читайте данную работу прямо на сайте или скачайте

Расчет распределения примесей в кремнии при кристаллизационной очистке и диффузионном легировании

Государственный комитет РФ по высшему образованию

Новгородский Государственный ниверситет

им. Ярослава Мудрого

Кафедра физики твердого тела и микроэлектроники

ФРАСЧЕТ РАСПРЕДЕЛЕНИЯ ПРИМЕСЕЙ

В КРЕМНИИ ПРИ КРИСТАЛЛИЗАЦИОНОЙ ОЧИСТКЕ

И ДИФФУЗИОННОМ ЛЕГИРОВАННИИФ

Пояснительная записк

к курсовой работе

Физико-химические основы технологии микроэлектроники

1998

Техническое задание

на курсовую работу по дисциплине

Физико-химические основы технологии микроэлектроники

Студенту гр. 7033 Родину Н.Е.

1. Рассчитать распределение примесей вдоль слитка полупроводникового материала при очистке зонной плавкой (один проход расплавленной зоной).

материал

примеси -

исходное содержание примесей (каждой)

Для трех скоростейа кр =1,5 ; 5 и 15 мм/мин.

2. Проанализировать бинарную диаграмму состояния Si -Ga а

оС; время диффузии - 30 мин.

оС и времени диффузии - 30 мин. словия перераспределения - полностью отражающая граница, температура 1150 ^оС, время 2 часа.

Срок сдачи законченнойа

Преподаватель........................................Б.М. Шишлянников

Студент

Реферат.

В курсовом проекте производится расчет распределения примеси вдоль слитка кремния зонной плавкой. Расчет производится для трех примесей (Ga,P и Sb) для трех скоростей (V_кр =1,5 ; 5 и 15 мм/мин). Кроме того расчет распределения Ga в кремнии после диффузионного отжига при различных словиях диффузии.

Курсовая работа содержит графики распределения примеси как при зонной плавке, так и при диффузии.

Содержание.

	Введени	5
1.	Расчетная часть..	6
1	Описание процесса зонной плавки и ее математическая модельЕЕ	6
1.2	Расчет распределения примеси вдоль слитка кремния после зонной плавки	10
1.2.1	Расчет распределения	10
1.2.2	Расчет распределения	13
1.2.3	Расчет распределения	14
1.3	Распределение примесей после диффузии.	18
1.3.1	Распределение примеси при диффузии из полубесконечного пространства (диффузия из концентрационного порога)..	21
1.3.2		22
1.3.3	Распределение примеси при диффузии из слоя конечной толщины	24
1.3.4	Распределение примеси при диффузии из бесконечно тонкого слоя в полубесконечное тело с отражающей границей	25
1.4	Расчет распределения примеси после диффузионного легирования.	28
1.4.1	Диффузия из бесконечного источника примеси на поверхности пластины	28
1.4.2	Диффузия из бесконечного источника примеси на поверхности пластины при Т=9500 С	29
1.4.3	Распределение примеси после перераспределения примеси накопленной в ОС и времени диффузии 30мин. словие перераспределения полностью отражающая граница. Т=1150ОС	30
	Заключени...	32
	Литература....	33

Введение.

Каждое вещество может находится в состоянии которое характеризуется содержанием примеси в нем ниже некоторого определенного предела. Предел определяется различными словиями связанными со свойствами, областью применения веществ. Для полупроводниковых материалов достижения собственных свойств или близких к ним является тем необходимым пределом до которого материалы должны очищаться. При обосновании необходимой очистки нужно руководствоваться и экономической целесообразности очистки.

Для очистки полупроводниковых материалов в технологии микроэлектронных стройств используется метод зонной плавки (перекристаллизация). В некоторых случаях в технологии полупроводниковых материалов выращивают монокристаллы методом зонной плавки. Достоинством метода является совмещение процесса глубокой очистки полупроводника с последующим выращиванием его монокристалла. В технологии разлагающихся полупроводниковых соединений применение этого метода позволяет совмещать в одном технологическом цикле сразу три операции

Для введения в полупроводник примеси используется процесс диффузии. Для изготовления

1.Расчетная часть.

           

1.1 Описание процесса зонной плавки и ее математическая модель.

нагреватель

расплав

закристаллизовавшаяся часть

кристалл

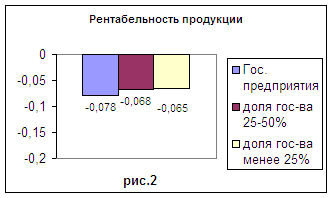
Рисунок1 Ц Схема зонной плавки.

Большинство примесей обладает хорошей растворимостью в жидкой фазе по сравнению с твердой (равновесный коэффициент сегрегации k0<0>

где N_тв - концентрация примеси в закристаллизовавшейся фазе на расстоянии x от начала слитка;

о Ц исходная концентрация примеси в очищаемом материале;

o

Если измерять длину слитка в длинах расплавленной зоны

Приведенные уравнения (1) и (2), являющиеся математическим описанием процесса зонной плавки,

1 тв = 0 ).

2

3

4 а

5тв=rж=r).

6

Уравнения (1) и (2)а

При a

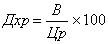
где g - доля закристаллизовавшегося расплава последнего частка.

Только при проведении процесса при словиях, когда довлетворяются все требования, приведенные выше, реальное распределение примеси в слитке после зонной плавки будет соответствовать закону, представленному выражениями (1) и (2).

анализ показывает, что в большинстве реально протекаемых процессов зонной очистки полупроводниковых материалов пфанновские допущения не реализуются. Вместе с тем, вывод равнений (1) и(2) без них был бы невозможен, менее жесткие допущения приводят к существенному сложнению получаемых выражений.

Наиболее жесткими являются словия 2 и 3.

Допущение 2 в данной формулировке может выполняться только при бесконечно малых скоростях кристаллизации (скорости движения зоны). В этом случае сравнительно быстрая (по сравнению с диффузией в твердой фазе) диффузия в жидкой фазе в состоянии постоянно выравнивать концентрации компонентов системы в объеме расплавленной зоны.

Использовании выражений (1) и (2) для представления распределения примеси при реальных скоростях кристаллизации приводит к необходимости изменить формулировку допущения 2. ж =

Условие полного перемешивания на практике реализовать невозможно. Процессы массопереноса в расплавленной зоне при реальных скоростях кристаллизации и разумной интенсивности перемешивании всегда приводят к образованию диффузионного слоя н эфф вместо равновесного k_o.

Равновесный коэффициент сегрегации связан с эффективным соотношением Бартона-Прима-Слихтера:

где акр - скорость перемещения расплавленной зоны (скорость кристаллизации);

ж -а

Эта замена является лишь более или менее дачным приближениема

Распределение примеси после зонной плавки для реальных процессов описывается выражением

Данное выражение позволяет анализировать влияние на сегрегационные процессы скорости перемещения зоны и словий перемешивания жидкой фазы.

Условие 3 справедливо только для сильно разбавленных растворов, т.е. при малых концентрациях примеси в системе. Кроме того, словие малости концентрации должно соблюдаться на протяжении всего процесса зонной плавки. Для того, чтобы

1.2 Расчет распределения примеси вдоль слитка кремния после зонной плавки (один проход расплавленной зоной)

1.2.1 Расчет распределения

Рассчитаем распределение галия в слитке кремния для трех скоростей перемещения зоны V_кр =1,5 ; 5 и 15 мм/мин.0

Распределение сурьмы вдоль слитка определяется равнением (5) на длине слитка а

При a

Прежде чем приступить к расчету переведем0-3. Для этого воспользуемся формулой перевода.

⁽⁶⁾

где А₁2ннЦатомные массы компонентов

2Цвторой компонент смеси.

томная массЦдля галлия = 69,72

Концентрация собственных атомов в кристаллической решетке кремния соб=522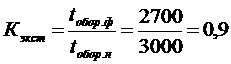 -3. Следовательно0=8,06-522=4,0318 -3

Для расчета эффективного коэффициента сегрегации воспользуемся выражением (4). Для галлия в кремнии 0=-3ж=200 с

Подставляя значения 0, ж, кр в (4)эфф. Для этого V_кр переведем из ммкр=2,5-3; 8,33-3; 2,5-2 эфф=1-2; 4,09-2; 0,545

тв вдоль слитка. При построении профиля, как правило, используют полулогарифмический масштаб, т.к. значения концентрации изменяются практически на три порядка.

а

Таблица 1 -а

Участока	Участок кристаллизации
	Nтв, см-3	r, (по кривым Ирвина)	g (a=10)	Nтв, см-3	r, (по кривым Ирвина)
кр-3 см
0	5,2416	0,42	0	4,9217	0,098
1	1,0417	0,28	0,2	6,1317	0,085
2	1,5417	0,21	0,4	8,1517	0,071
3	2,0417	0,18	0,6	1,2218	0,06
4	2,5417	0,15	0,8	2,4118	0,032
5	3,0317	0,14	0,9	4,7718	0,02
6	3,5117	0,13	0,99	4,6319	0,0028
7	3,9817	0,11	Ц	Ц	Ц
8	4,4517	0,1	Ц	Ц	Ц
9	4,9217	0,098	Ц	Ц	Ц
кр-3
0	1,617	0,2	0	1,3518	0,05
1	3,217	0,135	0,2	1,6718	0,048
2	4,6817	0,098	0,4	2,218	0,036
3	6,1117	0,085	0,6	3,2518	0,028
4	7,4817	0,075	0,8	6,3218	0,017
6	1,018	0,061	0,9	1,2319	0,009
7	1,1318	0,055	0,99	1,1220	0,0011
8	1,2418	0,051	Ц	Ц	Ц
9	1,3518	0,05	Ц	Ц	Ц
кр-2 см
0	2,218	0,036	0	4,0218	0,0215
1	2,9718	0,029	0,2	4,4518	0,021
2	3,4118	0,025	0,4	5,0718	0,019
3	3,6718	0,023	0,6	6,118	0,017
4	3,8218	0,0225	0,8	8,3618	0,0125
6	3,9618	0,0	0,9	1,1519	0,01
7	3,9818	0,022	0,99	3,2719	0,0037
8	4,0118	0,0215	Ц	Ц	Ц
9	4,0218	0,0215	Ц	Ц	Ц

r, кр-3 см кр-3 кр-2 см

1.2.2 Расчет распределения

Расчет распределения фосфора в кремнии будем производить аналогично расчету галлия в слитке кремния (пункт 1.2.1)

Переведем 0-3. Атомная масса фосфора = 30,97

N₀-2 % (атомных) = 9,0518 см^-3.

Для расчета эффективного коэффициента сегрегацииэфф воспользуемся выражением (4). Для фосфора в кремнии 0=-1ж=200 с

Подставляя значения 0, ж, кр в (4)эфф. Для трех скоростей кристаллизации V_кр=2,5-3; 8,33-3; 2,5-2 эфф=0,47

Заполним расчетную таблицу.

Таблица 2 -а

Участока	Участок кристаллизации
	Nтв, см-3	r, (по кривым Ирвина)	g (a=10)	Nтв, см-3	r, (по кривым Ирвина)
кр-3 см
0	4,2518	0,012	0	918	0,0068
1	6,0518	0,009	0,2	1,0119	0,006
2	7,1818	0,0075	0,4	1,1819	0,0058
3	7,8818	0,0073	0,6	1,4619	0,0042
4	8,3218	0,0071	0,8	2,1119	0,0034
5	8,618	0,007	0,9	3,0519	0,0024
6	8,7618	0,0069	0,99	1,0320	0,85
7	8,8718	0,0069	Ц	Ц	Ц
9	918	0,0068	Ц	Ц	Ц
кр-3
0	6,6918	0,0085	0	9,0518	0,0066
1	7,9318	0,0075	0,2	9,5918	0,0063
2	8,5118	0,0071	0,4	1,0319	0,006
3	8,818	0,0069	0,6	1,1519	0,0057
4	8,9318	0,0068	0,8	1,3819	0,0052
5	918	0,0068	0,9	1,6519	0,0045
7	9,0318	0,0066	0,99	319	0,0024
8	9,0418	0,0066	Ц	Ц	Ц
9	9,0518	0,0066	Ц	Ц	Ц
кр-2 см
0	8,9618	0,0068	0	9,0518	0,0066
1	9,0118	0,0068	0,2	9,0718	0,0066
2	9,0318	0,0066	0,4	9,118	0,0065
3	9,0518	0,0066	0,6	9,1318	0,0065
4	Ц	Ц	0,8	9,218	0,0064
5	Ц	Ц	0,9	9,2618	0,0064
9	9,0518	0,0066	0,99	9,4818	0,0063

r,

кр-3 см кр-3 кр-2 см

1.2.3 Расчет распределения

Расчет распределения сурьмы в кремнии будем производить аналогично расчету галлия в слитке кремния (пункт 1.2.1)

Переведем 0-3. Атомная масса сурьмы = 121,7

N₀-3 % (атомных) = 2,3118 см^-3.

Для расчета эффективного коэффициента сегрегацииэфф воспользуемся выражением (4). Для сурьмы в кремнии 0=-3ж=200 с

Подставляя значения 0, ж, кр в (4)эфф. Для трех скоростей кристаллизации V_кр=2,5-3; 8,33-3; 2,5-2 эфф=3,74-2

Заполним расчетную таблицу.

Таблица 3

Участока	Участок Кристаллизации
	Nтв, см-3	r, (по кривым Ирвина)	g (a=10)	Nтв, см-3	r, (по кривым Ирвина)
кр-3 см
0	8,6416	0,11	0	7,2217	0,028
1	1,6817	0,075	0,2	8,9517	0,023
2	2,4717	0,052	0,4	1,1818	0,0215
3	3,2217	0,047	0,6	1,7418	0,0192
4	3,9517	0,04	0,8	3,418	0,014
5	4,6617	0,038	0,9	6,6218	0,0082
6	5,3317	0,033	0,99	619	0,00135
7	617	0,031	Ц	Ц	Ц
9	7,2217	0,028	Ц	Ц	Ц
кр-3
0	2,5417	0,051	0	1,5518	0,02
1	4,6817	0,038	0,2	1,8918	0,018
2	6,617	0,03	0,4	2,4418	0,016
3	8,3217	0,027	0,6	3,518	0,013
4	9,8617	0,024	0,8	6,4918	0,0085
5	1,1218	0,022	0,9	1,219	0,0055
7	1,3618	0,0205	0,99	9,319	0,88
8	1,4618	0,02	Ц	Ц	Ц
9	1,5518	0,02	Ц	Ц	Ц
кр-2 см
0	1,818	0,019	0	2,3118	0,0157
1	2,0818	0,017	0,2	2,4218	0,0156
2	2,218	0,016	0,4	2,5818	0,015
3	2,2618	0,0158	0,6	2,8218	0,014
5	2,318	0,0157	0,8	3,2918	0,0137
7	2,3118	0,0157	0,9	3,8318	0,012
9	2,3118	0,0157	0,99	6,3618	0,0086

кр-3 см кр-3 кр-2 см

r,

На основании полученных данных построим графики распределения примесей вдоль слитка кремния после зонной плавки (один проход расплавленной зоной).

Nтв, -3 19 18

N0

Nтв, -3 19 18 17

N0

Nтв, -3 1019 1018 1017 1016

N0

Рисунок 5 - Распределение примесей после одного прохода расплавленной зоной при зонной плавке вдоль слитка

кр-3 см кр-3 кр-2 см

кр-3 см кр-3 кр-2 см

кр-3 см кр-3 кр-2 см

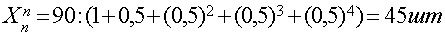
1.3. Распределение примесей после диффузии.

Основой математического описания процессов диффузии являются два дифференциальных уравнения Фика (немецкий ченый A. Fick предложил их в 1855 г.).

Первое равнение

где J - плотность потока диффундирующего вещества, т.е. количество вещества, проходящего за единицу времени через единичную площадь поверхности, перпендикулярной направлению переноса вещества;

N

D

Физический смысл этого равнения - первопричиной диффузионного массопереноса вещества является градиент его концентрации. Скорость переноса пропорциональна градиенту концентрации, в качестве коэффициента пропорциональности вводится коэффициент диффузии. Знак минуса

В макроскопическом представлении коэффициент диффузии 2/с. В общем случае диффузия анизотропна и коэффициент диффузии - симметричный тензор второго ранга.

Согласно микроскопическому определению, компонента D_x коэффициент

Когда концентрация вещества изменяется только в одном направлении (одномерная диффузия)а

При простейшем анализе структур и в простейших моделях процессов легирования в технологии изготовления ИМС предполагаются именно такие словия диффузии.

Второе равнение

В общем случае второе равнение диффузии имеет следующий вид

Для одномерной диффузии в изотропной среде равнение (9)а

Второй закон Фика характеризует процесс изменения концентрации диффундирующей примеси во времени в различных точках среды и является математической моделью нестационарного (развивающегося) состояния системы (описывает период времени от начала процесса до становления стационарного состояния).

При постоянстве коэффициента диффузии D (независимости его от концентрации примеси) равнение (10) прощается

Допущение о постоянстве коэффициента диффузии справедливо в большом количестве случаев, анализируемых в технологии ИМС.

Уравнения диффузии являются чисто феноменологическими, т.е. они не содержат никаких сведений о механизмах диффузии - о диффузионном процессе на атомном,

Процессы диффузии, используемые для изготовления интегральных структур, обычно анализируются с помощью частных решений уравнения (11) т.к., в отличие от (8), именно оно содержит важный параметр - время становления некоторого анализируемого состояния системы.

Общее решение равнения (11) для бесконечного твердого тела при заданном в общем, виде начальном распределении примеси а

здесь

Бесконечным в одномерном представлении называют тело, простирающееся от x=0 до x=-

Часто при поиске распределения концентрации примеси в полупроводнике необходимо решение уравнения (11) для полубесконечного твердого тела. Полубесконечным в одномерном представлении называют тело, простирающееся от x=0 до x=+

Для этого случая выражение (12) может быть приведено к виду

В выражении (13) знак плюс относится к ситуации, когда граница твердого тела (x=0) является непроницаемой для диффундирующего вещества, находящегося в области x>0,

Представленные решения позволяют находить

1.3.1а

Диффундирующая примесь (диффузант) поступает в полубесконечное тело через плоскость x=0 из второго полубесконечного тела (источника) с равномерным распределением примеси. Концентрация примеси в источнике - N_o. Полагается, что в принимающем диффузант теле нет рассматриваемой примеси.

Начальное распределение концентраций для этого случая задается в виде

N(x,0) = N_o для

N(x,0) = 0для а

Решением уравнения (11) для этого случая является выражение

Второе слагаемое в квадратных скобках называют а

В математике часто используют как самостоятельную и другую функцию

erfc

которая называется дополнением функции ошибок до единицы или дополнительной функцией ошибок - error function complement. Обе функции табулированы.

Таким образом, выражение (1

Величина

Рассмотренное решение можно использовать как простейшую модель, представляющую распределение примеси в автоэпитаксиальной структуре. При этом, в качестве независимых источникова

1

Диффузант поступает в полубесконечное тело через плоскость x=0 из источника, обеспечивающего постоянную концентрацию примеси N_o на поверхности раздела твердое тело - источник в течение любого времени. Такой источник называют бесконечным или источником бесконечной мощности. Полагается, что в принимающем диффузант теле нет рассматриваемой примеси.

Начальное распределение концентрацийа

N(x,t) = N_o для

N(x,0) = 0для а

Решением уравнения (16) для данных словий является выражение

Если в объеме полупроводникового материала до диффузии имелась примесь противоположного типа по отношению к диффундирующей, эта примесь распределена по объему равномерно и её концентрация равна N_b, то в этом случае в полупроводнике образуется электронно-дырочный переход. Его положение (глубина залегания) x_j определяется словием N(x,t)=N_b , откуда

и

здесь запись erfc^-1 а

При решении практических задач, связанных с анализом диффузионных процессов необходимо знать количество примеси Q, накопленной в твердом теле при диффузии в течение времени t. Эта величина определяется по формуле

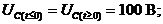
где J(0,t) - поток диффузанта в объем через плоскость x=0

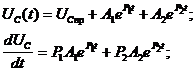
отсюда

Следует обратить внимание на возрастающее со временем значение накопленной в диффузионном слое примеси при диффузии с данными граничными словиями.

Рассмотренная модель диффузионного процесса с постоянным источником описывает процесс диффузионного легирования полупроводникового материала из газовой или паровой фазы. Этот процесс используется при создании сильно легированных диффузионных слоев (например, эмиттерных) с поверхностными концентрациями N_o близкими к значениям предельной твердой растворимости примеси в данном полупроводниковом материале.

Твердое тело можно считать полубесконечным ( или бесконечным) в том случае, если его размеры в направлении движения диффузанта много больше длины диффузии.

1.3.3 Распределение примеси при диффузии из слоя конечной толщины

Диффундирующая примесь поступает в полубесконечное тело из источника, который представляет собой примыкающий к границе тела слой толщиной h, примесь в котором распределена равномерно. Такой источник называют ограниченным. Концентрация примеси в источнике - N_o. Полагается, что в принимающем диффузант твердом теле нет рассматриваемой примеси.

При абсолютно непроницаемой для диффузанта (отражающей) границе поток примеси через поверхность x=0 должен обращаться в нуль при всех t

Начальное распределение концентраций для рассматриваемого случая задаётся в виде

N(x,0) = N_o для 0

N(x,0) = 0для а

Граничным условием является, определяемое словием (24), постоянство количества примеси в источнике и полупроводнике

Для реализации начального распределения такого типа диффундирующая примесь должна быть введена в твердое тело до начала диффузии.

Решением уравнения (16) в данной ситуации является выражение

Здесь следует отметить, что erfс(-z) + erfс(z)

В отличие от диффузии из постоянного источник oh. В процессе диффузии происходит только его перераспределение и, следовательно, меньшение со временем концентрации примеси на поверхности твердого тела.

Примером диффузии примеси из слоя конечной толщины в полубесконечное тело с отражающей границей является диффузия в кремниевую пластину из эпитаксиального, имплантированного или диффузионного слоя и покрытую слоем двуокиси кремния SiO₂ или нитрида кремния Si₃N_4. Границу пластины и пленки можно с большой долей правдоподобия принять отражающей, т.к. коэффициенты диффузии большинства примесей в кремнии на несколько порядков больше, чем в двуокиси кремния и нитриде. Однако, равномерность распределения примеси в источнике, особенно при его создании методом диффузии или имплантации - весьма грубое и вынужденное приближение.

1.3.4а

Решение диффузионного равнения при этих словиях находится из предыдущего при hoh.

Приведенное выражение представляет собой Гауссово распределение.

Тонкий слой на поверхности полупроводниковой пластины является источником, который очень быстро истощается. Непрерывная диффузия в этом случае приводит к постоянному понижению поверхностной концентрации примеси в полупроводнике. Эту особенность данного процесса используют в полупроводниковой технологии для получения контролируемых значений низкой поверхностной концентрации примеси, например, для создания базовых областей кремниевых транзисторных структур дискретных приборов или ИМС.

На первом этапе процесса проводится кратковременная диффузия (при пониженных температурах) из постоянного источника, распределение примеси после которой описывается выражением (18). Значение N_o при этом велико и определяется либо пределом растворимости данной примеси в полупроводниковом материале, либо концентрацией примеси в стеклообразном слое на поверхности полупроводника. Этот этап часто называют загонкой. После окончания первого этапа пластины помещают в другую печь для последующей диффузии, обычно, при более высоких температурах. В этой печи нет источника примеси, если он создается на первой стадии в виде стеклообразного слоя на поверхности пластин, его предварительно даляют. Таким образом, тонкий слой, полученный на первом этапе, является источником перераспределяемой примеси при проведении второй стадии процесса. Для создания отражающей границы 2.

Существует заметное несоответствие между распределением примеси в источнике, сформированном при загонке, с декларируемым при выводе выражений (25) и (26) - ступенчатым. Это несоответствие должно отразиться

При моделировании двухстадийной диффузии и анализе результатов процесса полагают, что выражение (26) достаточно точно соответствует реальному при словии, если величина произведения D₁t₁ для первого этапа процесса легирования значительно меньше, чем D₂t₂ для второго -

из (26) получим

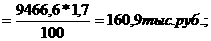
Величины D₂ и t₂ относятся ко второй стадии диффузии.

В случае, если продолжительность второй стадии не очень велика по сравнению с первой, или, иными словами, D₂t₂1t₁

где

Поверхностная концентрация примеси после второй стадии диффузии выражается при данных словиях соотношением

Выражение (25) используется для представления распределения при словии, что D₁t₁ >D₂t_{2 аа. При этом полагают, что}

1.4

1.4.1 Диффузия из бесконечного источника примеси на поверхности пластины

Материал - кремний

примесь - галлий.

Условия проведения диффузии

Температуру соответствующую максимальной растворимости галлия в кремнии

Nпред. раств.=0=619 см^-3

Коэффициент диффузии сурьмы при температуре диффузии найдем

где предэкспоненциальный множитель (постоянная диффузии) D_{oа и энергия активации диффузии}

k

Из [5] аo =0,374 см²/с, -12 см²/с.

Заполняем расчетную таблицу, меняя расстояние от x поверхности с необходимой частотой, до значения при котором значение 12. В первый столбец записываем выбранные значения x, во второй -

Таблица 4 - Результаты расчета распределения галлия в кремнии

x, мкм		erfc(z)	N(x), см-3	x, мкм		erfc(z)	N(x), см-3
0	0	1	619	2,5	2,12	0,002716	1,6317
0,5	0,42	0,552532	3,3219	3	2,54	0,328	1,96816
1	0,85	0,229332	1,37619	3,5	2,96	0,28	1,6815
1,5	1,27	0,072486	4,3518	4	3,38	0,1753	1,0514
2	1,69	0,016847	1,01218	4,5	3,8	0,77	4,6212

Рисунок 6 Ц (полулогорифмический масштаб по оси концентраций)

мкм

119

117

113

115

см-3

N

x

1.4.2 Диффузия из бесконечного источника примеси на поверхности пластины при Т=950⁰ С=1223а

Коэффициент диффузии 0 С0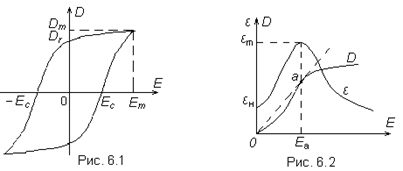=19см^-3.

Диффузия проходит согласно выражению (

x, мкм		erfc(z)	N(x), см-3	x, мкм		erfc(z)	N(x), см-3
0	0	1	319	0,1	2,05	0,003742	1,12317
0,02	0,41	0,562031	1,686119	0,12	2,46	0,503	1,5091016
0,04	0,82	0,246189	7,38618	0,14	2,87	0,49	1,4715
0,06	1,23	0,08195	2,458518	0,16	3,28	0,35	1,0514
0,08	1,64	0,020378	6,113417	0,18	3,69	0,18	5,412

Полученные результаты используются для построения графика N = f(x) - примесного профиля. При построении профиля, как правило, используют полулогарифмический масштаб.

119

117

113

115

см-3

N

x

мкм

Рисунок 7 Ц (полулогорифмический масштаб по оси концентраций)

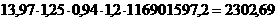1.4.3 Распределение примеси после перераспределения примеси накопленной в приповерхностном слое полупроводника при Т=950^ОС=1223 К и времени диффузии 30мин=1800с. словие перераспределения полностью отражающая граница. Т=1150^ОС=1423 К

Произведение D₁t₁ для процесса загонки равно: D₁t₁ = 3,31-15 5,958-12а см²

Коэффициент диффузии для процесса перераспределения примеси (D_o =0,374 см²/с, -13 см²/с. Произведение D₂t₂ = 3,128-13 2,25-9а см². D₂t₂ > D₁t_{1 (в 377 раз), т.е. словия быстрой истощаемости источника, следовательно, пользуемся для расчета распределения примеси выражением (}

В первый столбец таблицы (6) заносим значения 2/4D₂t₂)s

Таблица 6 - Результаты расчета распределения галлия в кремнии при диффузии из приповерхностного слоя.

x, мкм		Ns, см-3	x, мкм		Ns, см-3
0	1,0	9,82317	1,8	0,02742	2,69316
0,36	0,866	8,50717	2,16	0,005633	5,53415
0,72	0,5624	5,52517	2,52	0,8681	8,52714
1,08	0,274	2,6917	2,88	0,1	9,85413
1,44	0,1	9,83116	3,24	0,87	8,54112

Рисунок 8 Ц (полулогорифмический масштаб по оси концентраций)

N

мкм

118

117

115

116

см-3

114

113

112

x

Заключение.

В данном курсовом проекте

Для процесса зонной плавки произведен расчет для трех очищаемых примесей

Эффективность очистки зависит от скорости кристаллизациикроэффо0кроэфф0) 0 _{Sb<k0 Ga<k0 P<}

анализ второй части расчета - метод введения и перераспределения примеси - диффузии показываета

Литература.

1.    

2.    

3.    

4.    

5.    

r

p - Si

n - Si

N

1012 13 14а 15 16 17а 18 19 20 21 -3

1×104

1×103

1×102

10

1×10-1

1

1×10-2

1×10-3

Ом × см

Зависимость дельного сопротивления а