Читайте данную работу прямо на сайте или скачайте

Примеры задач оптимизации, связанных с фундаментальными понятиями теории связи

Министерство образования и науки

Республики Казахстан

Казахско - Американский ниверситет

Факультет Прикладных наук

СРС

Тема:а

Студент:

Группа: ФПН (РРТ)-5с

Проверил:.

Дата:

Подпись

лматы, 2005

Примеры задач оптимизации, связанных с фундаментальными понятиями теории связи.

Приводимые ниже две задачи оптимизации типичны; такого

при наличии шума с неравномерным спектром; вторая -с выбором формы импульсного сигнала, обладающего мининмально возможной полосой частот и потому наиболее адекватнного работе по полосно-ограниченному каналу связи. Обе эти задачи имеют самостоятельный интерес; вместе с тем они могут рассматриваться как достаточно простые пражнения по практическому применению

Экстремальная

канала связи

Максимальное количество информации, которое может быть передано за единицу времени по каналу связи с полосой

где

Если спектральные плотности мощности сигнала и шума 1, f

где

Ч

Поставим задачу об отыскании спектра плотности мощности С =и заданной спектральной

При дополнительном словии

Используя терминологию предыдущего раздела, можно говорить что поставленная задача является изопериметрической

Составив в соответствии с методом множителей Лагранжа вспомогательныйа

выпишем для

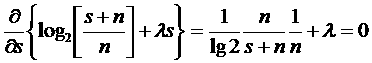
откуда

Подставляя

находима

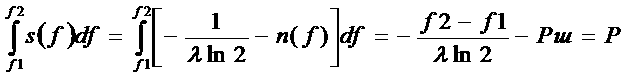
Окончательно

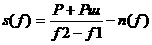
Как видно, оптимальный спектр плотности мощности сигнала

Этот вывод представляет несомненный практический интенрес, однако он, может быть, сделан поспешно, ведь не

В связи с записью приближенного равенства

Однако неравенство (3.24) может оказаться нарушенным:

S

На решениях задач подобного типа мы останавливаться

Задач

ширинойа

Как правило, передача информации по каналам связи

Сказанное,

Преобразование Фурье сигнала конечной продолжительн

переменного ω

Известно, что целые функции могут обращаться в 0 лишь

и т. д. Практически это означает, что спектры сигналов

Существуют различные способы оценки внеполосных

Задаче минимизации величины а

решают вопрос о максимизации энергии импульса y

Напомним,

поэтому

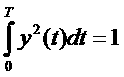
3.31

Вариационную задачу максимизации (3.29) при словии

как плотность распределения вероятностей

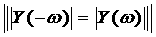
то среднее значение этой случайнойа

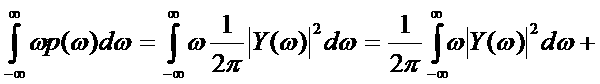
Положительную величину спектра сигнала

равенство (3.28), которое отражает известное свойство интегнрала от плотности распределения вероятностей (он равен

Здесь местно напомнить, что дисперсия характеризует степень

Выражение (3.32) преобразуем таким образом, чтобы предн

Продифференцируема

Применим теперь теорему РэлеяПарсеваля к сигналу

Сравнив равенств

Для минимизации функционала (3.36) при ограничении

Сделаем прощающее предположение (оно облегчит, как мы видим, проверку достаточных словий минимизации): импульс

функционал

при

Правый конец отрезка [О, Т/2 ] будем считать свободным, т. е. предполагать, что у{Т/2) может принимать любые знан

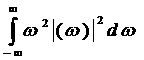
значит, и существования конечной величины 4 при

Но

y

Так как вне отрезка

или

Уравнение Эйлера для функционала (3.38)

y

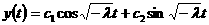
Таким образом,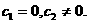

Для определения 1 = 0):

откуда

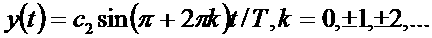
где с₂ и целое число 2 а

Несколько сложнее найти число

т. е. совпадает по форме с равнением Эйлера рассматриваемой

Для выполнения словия

обладают дополнительными нулями на

отрезке (0,

Ч полуволну синуса¹. Чтобы доказать, что (3.46) действительно

Определение константы с₂, как же говорилось, не вызывает затруднений, она равна

В заключение разъясним, в чем трудность исследования о = 0 при

Замечание 3.5. Задача минимизации полосы частот,