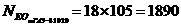Читайте данную работу прямо на сайте или скачайте
Построение оптимального производственного плана химической компании
Содержание
Экономическая постановка задачи........................................................3
Математическая постановка задачи......................................................4
Описание и теоретическое обоснование алгоритма решения.............5
Решение задачи. Стохастическое программировани11
Метод линейных комбинаций...15
Выводы.19
Список использованной литературы.20
Экономическая постановка задачи
Предприятие химической промышленности ЗАО Химсервис планирует выпустить 2 новых вида кислот. С этой целью был проведён ряд исследований, в результате которых стало очевидно, что вред окружающей среде от искомого производства составит соответственно 10 и 20% от всей продукции в стоимостном выражении.
Государство вводит экологические санкции за превышение лимита допустимой концентрации казанных отходов в реке (он составляет 100 литров в квартал).
Себестоимость продукции предприятия прогнозируется независимо по каждому виду товара на основании практических данных по сходным по технологии производства видам, причём достоверность прогноза не менее 0,9 и 0,8 по каждому виду продукции соответственно.
Необходимо произвести оценку себестоимости продукции и составить оптимальный производственный план за квартал, учитывающий данную оценку, если известно, что Химсервис заключил договор поставки с парфюмерной компанией Парфюм, который предусматривает реализацию кислотной продукции по ценам 15 и 20 тысяч рублей за литр соответственно.
Математическая постановка задачи
Исходная задача эквивалентна следующей:
z = (15 - m) * x1 + (20 - n) * x2 Ц > max
x1 + 2 * x2 ≤ 1
P {m ≥ M} ≥ 0.9
P {n ≥ N} ≥ 0.8
В данной символической записи x1, x2, m, n, M, N представляют собой, соответственно, количество планируемой к производству кислоты по видам, себестоимость продукции по видам и их минимально возможные показатели, представленные случайными величинами. Известна также информация оценки себестоимости продукции по технологически сходным видам.
Таблица 1
Оценка себестоимости продукции
Описание и теоретическое обоснование алгоритма решения
Прежде всего необходимо свести задачу к детерминированному виду. Для этого достаточно знать на заранее известном ровне значимости α законы распределения случайных величин. Определить его можно путём анализа статистических данных, приведённых в таблице 1. При проверке выборок на принадлежность их к закону распределения, тип которого можно оценить с помощью гистограммы и эмпирической функции распределения, используется критерий согласия Колмогорова-Смирнова.
Определим расстояние Колмогорова между эмпирической и теоретической функциями распределения:
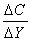
Соответствующее решающее правило критерия: H0 верна, если  H1. Здесь статистика
H1. Здесь статистика  апри достаточно большом
n асимптотически стремится к распределению Колмогорова, которое не зависит от F(x).
апри достаточно большом
n асимптотически стремится к распределению Колмогорова, которое не зависит от F(x).
Для того чтобы пользоваться казанным критерием необходимо провести группировку исходной выборки по интервалам, построить соответствующие гистограмму и эмпирическую функции распределения. Наконец, для оценки значений теоретической функции распределения необходимо оценить параметры подбираемого распределения.
После становления на ровне значимости α справедливости гипотезы H0 можно преобразовать казанные вероятностные ограничения к эквивалентным детерминированным. Это можно сделать следующим образом:
 X же здесь представлен в виде:
X же здесь представлен в виде: 
Очевидно, что целевая функция - это функция четырёх переменных, все ограничения модели линейны,
так как преобразованные вероятностные ограничения представляют собой функции распределения с аргументом 

Теперь можно с полным правом использовать метод линейных комбинаций. Его общая постановка выглядит следующим образом:

Здесь X, Ai, Bj - векторы переменных, соответствующих им коэффициентов и правых частей ограничений соответственно. Также выполнены словия k<n<m.
Суть метода линейных комбинаций заключается в итерационном использовании понятия градиента функции (обозначается grad z). По определений градиент функции записывается математически как
 n-мерный вектор, координаты которого представлены частными производными соответствующей функции (важно заметить, что функция z должна иметь конечные частные производные). Градиент покатывает направление, при движении по которому можно достичь максимума функции на минимальное число итераций, позволяющих на основании исходных координат вектора переменных сформировать новый вектор переменных, который будут находиться ближе к оптимуму. Очевидно, что данный подход (он основан на равенстве grad z=0, которое в силу определения градиента эквивалентно необходимому словию существования экстремума у функции z) может вывести за пределы области ограничений задачи. К тому же, в точке словного оптимума градиент функции z не обязательно равен нулю. Поэтому применяется следующий алгоритм решения задачи.
n-мерный вектор, координаты которого представлены частными производными соответствующей функции (важно заметить, что функция z должна иметь конечные частные производные). Градиент покатывает направление, при движении по которому можно достичь максимума функции на минимальное число итераций, позволяющих на основании исходных координат вектора переменных сформировать новый вектор переменных, который будут находиться ближе к оптимуму. Очевидно, что данный подход (он основан на равенстве grad z=0, которое в силу определения градиента эквивалентно необходимому словию существования экстремума у функции z) может вывести за пределы области ограничений задачи. К тому же, в точке словного оптимума градиент функции z не обязательно равен нулю. Поэтому применяется следующий алгоритм решения задачи.
Пусть Xk - допустимая точка, полученная на k-ой итерации. Раскладывая исходную функцию в ряд Тейлора, имеем  X и Xk - векторы. Необходимо определить допустимую точку X=X*, в которой достигается максимум функции f(X) при выполнении линейных ограничений задачи. Так как
X и Xk - векторы. Необходимо определить допустимую точку X=X*, в которой достигается максимум функции f(X) при выполнении линейных ограничений задачи. Так как 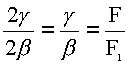 а- постоянное слагаемое, задача определения X* сводится к решению задачи линейного программирования:
а- постоянное слагаемое, задача определения X* сводится к решению задачи линейного программирования:

Так как целевая функция wk определяется градиентом функции f(X) в точке Xk,
улучшение имеющегося решения может быть обеспечено тогда и только тогда, когда  f(X*) > f(Xk), так как X* не обязательно находится в малой окрестности точки Xk. Но при выполнении словия
f(X*) > f(Xk), так как X* не обязательно находится в малой окрестности точки Xk. Но при выполнении словия  ана отрезке [Xk,X*] должна существовать точка Xk+1, такая, что f(Xk+1) > f(Xk).
Следовательно, задача сводится к нахождению такой точки Xk+1. Определим казанную точку следующим образом:
ана отрезке [Xk,X*] должна существовать точка Xk+1, такая, что f(Xk+1) > f(Xk).
Следовательно, задача сводится к нахождению такой точки Xk+1. Определим казанную точку следующим образом:
Отсюда следует, что точка Xk+1 является линейной комбинацией точек Xk и X*, значит это точки выпуклой области допустимых решений, поэтому точка Xk+1 также является допустимой. Так как Xk+1 зависит лишь ота r, то Xk+1 определяется путём максимизации функции  k-ой итерации не будет выполнено словие
k-ой итерации не будет выполнено словие  Xk считается наилучшим решением.
Поскольку задачи линейного программирования, возникающие на каждой итерации,
отличаются друг от друга лишь коэффициентами целевой функции, можно применить анализ чувствительности к соответствующим изменениям.
Xk считается наилучшим решением.
Поскольку задачи линейного программирования, возникающие на каждой итерации,
отличаются друг от друга лишь коэффициентами целевой функции, можно применить анализ чувствительности к соответствующим изменениям.
Теперь вкратце необходимо описать применение обобщённого симплекс-метода (сочетает в себе прямой и двойственный симплекс методы) для решения задачи линейного программирования. Рассмотрим для начала симплекс-таблицу и правила её построения.
Таблица 2
Пример симплекс-таблицы
|
Базис |
X1 |
X2 |
X3 |
X4 |
Решение |
|
Z |
-1 |
-2 |
0 |
0 |
0 |
|
X3 |
2 |
1 |
1 |
0 |
3 |
|
X4 |
3 |
4 |
0 |
1 |
2 |
Эта таблица представляет собой начальную симплекс-таблицу и эквивалентна следующей задаче линейного программирования:
 ó
ó 
Здесь переменные X3, X4 являются вспомогательными для получения начального базисного решения. Если бы неравенства имели знак ≥, то они вычитались бы из их левых частей.
После того как сформировано начальное базисное решение, проводятся операции по его лучшению, сохраняя при этом допустимость решения. В задаче максимизации целевой функции оптимум достигается тогда и только тогда, когда коэффициенты при небазисных переменных становятся положительными. Итерации симплекс-метода подвергаются условиям оптимальности и допустимости.
Условие допустимости: в качестве исключаемой переменной из базиса выбирается такая, для которой отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если переменных с таким свойством несколько, то выбирается любая из них.
Условие оптимальности: в качестве вводимой переменной в задаче максимизации является небазисная переменная, имеющая наибольший отрицательный коэффициент в z-строке. Если переменных с таким свойством несколько, то выбирается любая из них.
Теперь можно привести последовательность действий прямого симплекс-метода:
находится начальное допустимое базисное решение;
на основе словия оптимальности определяется вводимая переменная. Если вводимых переменных нет, вычисления заканчиваются;
на основе словия допустимости выбирается исключаемая переменная;
методом Гаусса вычисляется новое базисное решение. Переход к шагу 2.
К сожалению, нахождение начального базисного решения можно обеспечить только лишь в случае, когда все ограничения задачи линейного программирования имеют знак ≤. В противном случае либо используют искусственные переменные, либо используют двойственный симплекс-метод в комбинации с прямым симплекс-методом (обобщённый симплекс-метод).
Идея двойственного симплекс-метода состоит в рассмотрении в качестве начального базиса оптимальное, но недопустимое решение (супероптимальное решение). То есть умножают неравенства со знаком ≥ на (-1). Таким образом, если в z-строке находится изначально оптимальное решение, то применим двойственный симплекс-метод.
Условие допустимости: в качестве исключаемой переменной выбирается такая, которая имеет наибольшее по абсолютной величине отрицательное значение. Если все базисные переменные неотрицательны, процесс вычислений заканчивается.
Условие оптимальности: вводимая переменная определяется, соответствующая словию 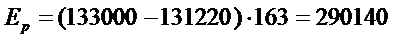 arj - коэффициент из симплекс-таблицы,
расположенный на пересечении ведущей строки (соответствующей исключаемой переменной xr), соответствующего переменной xj. При наличии альтернативы выбор делается произвольно.
arj - коэффициент из симплекс-таблицы,
расположенный на пересечении ведущей строки (соответствующей исключаемой переменной xr), соответствующего переменной xj. При наличии альтернативы выбор делается произвольно.
Однако, при умножении неравенств со знаком ≥ на (-1) начальное базисное решение может оказаться неоптимальным и недопустимым. В таких случаях применяется обобщённый симплекс-метод: сначала применяем двойственное словие допустимости. Выбор вводимой переменной осуществляется с применением двойственного словия оптимальности. Описанная процедура повторяется до тех пор, пока не будет получено допустимое решение. Далее применяется прямой симплекс-метод, где начальное базисное решение же соответствует словию допустимости, но не является оптимальным.
В завершении обзора алгоритма решения искомой задачи опишем метод анализа чувствительности оптимального решения задачи линейного программирования к изменению коэффициентов целевой функции. Для этого рассмотрим фрагмент симплекс-таблицы и некую задачу линейного программирования в матричном виде:

Таблица 3
Фрагмент матричной симплекс-таблицы
|
Базис |
ЕxjЕ |
Xб |
Решение |
|
z |
zj-cj |
||
|
Xб |
B-1Pj |
B-1 |
B-1b |
Введём теперь понятие двойственной задачи:
Обозначим через Y m-мерный вектор переменных двойственной задачи. В компактной матричной форме можно записать Y=CбB-1, где Cб - m-мерный вектор, состоящий из коэффициентов cj исходной целевой функции,
соответствующих базисному вектору Xб. Таким образом, разности zj-cj можно определить следующим образом: 
для любой симплекс-таблицы прямой или двойственной задачи справедливо: коэффициент при j-ой переменной в z-строке одной задачи равен разности между левой и правой частями j-го неравенства другой задачи;
для любой пары допустимых решений прямой и двойственной задач выполняется: значение целевой функции в задаче максимизации ≤ значения целевой функции в задаче минимизации. В точке оптимума наблюдается строгое равенство.
Таблица 4
Соотношение прямой и двойственной задачи
|
Прямая задача |
Двойственная задача |
|
|
|
Тем самым можно вычислить новые значения коэффициентов z-строки окончательной симплекс-таблицы по изменённым исходным данным задачи. В этом и состоит суть анализа чувствительности к изменению коэффициентов целевой функции. В задаче максимизации на коэффициенты при небазисных переменных z-строки накладываются ограничения неотрицательности, что позволяет найти интервалы допустимости для коэффициентов целевой функции, либо составить систему неравенств, описывающую их.
Решение задачи
Стохастическое программирование
Проведём анализ выборок из генеральных совокупностей M и N на основании данных, приведённых в таблице 1. Для построения таких таблиц необходимо построить точечные оценки параметров распределения генеральных совокупностей. Наилучшими такими оценками для математического ожидания и дисперсии являются выборочное среднее и выборочная дисперсия при неизвестном математическом ожидании соответственно.
Они рассчитываются как 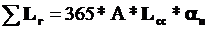 ni и xi - частота и середина i-го интервала соответственно.
Подставляя в формулы данные таблицы 1 и учитывая группировки данных,
представленных в таблицах 5 и 6, имеем:
ni и xi - частота и середина i-го интервала соответственно.
Подставляя в формулы данные таблицы 1 и учитывая группировки данных,
представленных в таблицах 5 и 6, имеем:

Таблица 5
анализ выборки из M
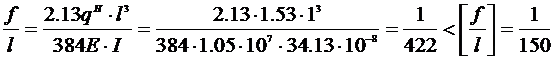
Таблица 6
анализ выборки из N

Здесь Fт представляет собой расчёт теоретической функции распределения, получаемый при оценивании параметров распределения наилучшими точечными оценками. Закон распределения предполагается нормальным в обоих случаях, так как вид гистограммы, построенной по исходным данным, является схожим графику плотности нормального распределения с параметрами, равными точечным оценкам.

рис. 1 Гистограмма M

рис. 2 Гистограмма N
Так как на основании гистограмм выдвинуто предположение о нормальности законов распределения M и N, то можно окончательно формировать таблицы 5 и 6, где  аи
аи 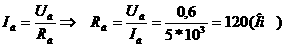 M и N:
M и N:

рис 3. Функции распределения M
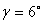
рис 4. Функции распределения N
Из рисунков видно, что данные выборок неплохо согласуются с теоретическими значениями, следовательно, имеет смысл применить критерий согласия Колмогорова-Смирнова для подтверждения на ровне значимости α = 0,01 гипотезы соответствия эмпирических данных теоретическому распределению.
По таблицам 5 и 6 вычисляем значения критериальной статистики при n = 30.
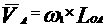 а- значит гипотеза верна.
а- значит гипотеза верна.
 а- гипотеза также верна.
а- гипотеза также верна.
Теперь можно преобразовать стохастические ограничения задачи в эквивалентные им линейные.
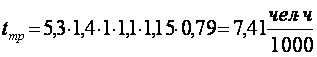

Заметим, что все преобразования законны, так как M - случайная величина, имеющая на ровне значимости α =
0,01 нормальное распределение с параметрами 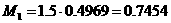
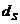 аимеет нормированное нормальное распределение с математическим ожиданием, равным нулю, и единичной дисперсией. Значит, функция распределения такой случайной величины будет эквивалентна табулируемой функции Лапласа, что позволяет в силу монотонности последней преобразовать эквивалентным образом стохастическое ограничение в линейное.
аимеет нормированное нормальное распределение с математическим ожиданием, равным нулю, и единичной дисперсией. Значит, функция распределения такой случайной величины будет эквивалентна табулируемой функции Лапласа, что позволяет в силу монотонности последней преобразовать эквивалентным образом стохастическое ограничение в линейное.
налогично для случайной величины N: 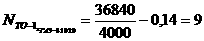
Таким образом, можно сформулировать задачу нелинейного программирования с линейными ограничениями:
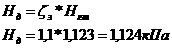 ó
ó 
Метод линейных комбинаций
Выберем произвольную начальную точку, довлетворяющую всем ограничениям задачи: X1 = (1; 1; 12; 4). Теперь можно вычислить градиент исходной целевой функции в точке X1: 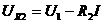
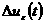 ó
ó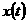
Поскольку последняя эквивалентность определяет стандартный вид задачи линейного программирования, можно построить начальную симплекс-таблицу, содержащую неоптимальное и недопустимое решение.
Таблица 7
Первая итерация
|
Базис |
x1 |
x2 |
m |
n |
S1 |
S2 |
S3 |
Решение |
|
w1 |
-3 |
-16 |
1 |
1 |
0 |
0 |
0 |
0 |
|
S1 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
1 |
|
S2 |
0 |
0 |
-25 |
0 |
0 |
1 |
0 |
-268 |
|
S3 |
0 |
0 |
0 |
-10 |
0 |
0 |
1 |
-33 |
Согласно обобщённому симплекс-методу для поиска исключаемой переменной из базиса пользуемся двойственным словием оптимальности - в данном случае исключаемой будет переменная S2. В качестве вводимой переменной по двойственному словий оптимальности выберем переменную m. Тем самым можно формировать следующую симплекс-таблицу. Получить новую симплекс-таблицу можно, используя метод Гаусса:
новая ведущая строка равна текущей строке, делённой на ведущий элемент;
новая строка равна разности текущей строки и новой ведущей строки, множенной на её коэффициент в ведущем столбце.
Таблица 8
Вторая итерация
|
Базис |
x1 |
x2 |
m |
n |
S1 |
S2 |
S3 |
Решение |
|
w1 |
-3 |
-16 |
0 |
1 |
0 |
|
0 |
|
|
S1 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
1 |
|
m |
0 |
0 |
1 |
0 |
0 |
|
0 |
|
|
S3 |
0 |
0 |
0 |
-10 |
0 |
0 |
1 |
-33 |
Теперь в качестве исключаемой переменной выберем S3, в качестве вводимой - n.
Таблица 9
Третья итерация
|
Базис |
x1 |
x2 |
m |
n |
S1 |
S2 |
S3 |
Решение |
|
w1 |
-3 |
-16 |
0 |
0 |
0 |
|
|
|
|
S1 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
1 |
|
m |
0 |
0 |
1 |
0 |
0 |
|
0 |
|
|
n |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
Недопустимость решения странена, значит, можно пользоваться прямым симплекс-методом. В качестве вводимой переменной берём x2 (имеет наибольший по модулю отрицательный коэффициент). Исключаемая из базиса переменная - S1, так как отношение числа в столбце Решение ведущей строки к ведущему элементу минимально по модулю).
Таблица 10
Четвёртая итерация
|
Базис |
x1 |
x2 |
m |
n |
S1 |
S2 |
S3 |
Решение |
|
w1 |
5 |
0 |
0 |
0 |
8 |
|
|
|
|
x2 |
|
1 |
0 |
0 |
|
0 |
0 |
500 |
|
m |
0 |
0 |
1 |
0 |
0 |
|
0 |
|
|
n |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
Текущее решение удовлетворяет словиям оптимальности и допустимости прямого симплекс-метода,
следовательно, в таблице 10 содержится оптимальное решение задачи линейного программирования w1. Запишем вектор, соответствующий данному решению: 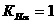 .
.
Для завершения решения задачи линейного программирования w1 необходимо провести анализ текущего оптимального решения на чувствительность. Имея формулировку прямой задачи, можно составить двойственную задачу:
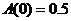 ó
ó 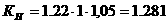
Пусть коэффициенты целевой функции w1 изменились, и вектор коэффициентов C запишется в виде: C = ( 3 + d1; 16 + d2; -1 + d3; -1 + d4 ). Так как текущее оптимальное решение представлено базисными переменными x2, m, n, то вектор базисных коэффициентов будет включать именно эти переменные: Cб = ( 16 + d2; -1 + d3; -1 + d4 ), обратная матрица B-1 - состоять из элементов таблицы 10, соответствующих по своему положению начальному базисному решению. Значит, вектор оптимальных двойственных переменных Y будет рассчитываться:
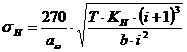

Теперь можно вычислить коэффициенты z-строки при небазисных переменных, учитывая фундаментальное соотношение между прямой и двойственной задачами:
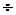 (1)
(1)
В итоге словие (1) является необходимым и достаточным для того, чтобы тверждать состоятельность текущего базисного решения при изменении коэффициентов целевой функции.
Так как 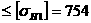 X2:
X2:
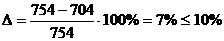 (2)
(2)
Подставляя в формулу (2) вычисленный ранее вектор X*, получим:
X2 = ( 1; 1; 12; 4 ) + r ( -1; 499;  ;
;  1- r; 1+
499r; 12
1- r; 1+
499r; 12  ; 4
; 4 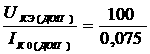 ).
).
Согласно методу линейных комбинаций вычислим максимум целевой функции z в точке X2:
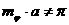
В итоге данная функция относительно r является квадратичной с положительным старшим коэффициентом - значит, своего минимума она достигнет при отрицательном r. Очевидно, при всех допустимых r функция монотонно возрастает - её
максимум совпадает с максимальных допустимым r. То есть 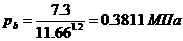 X2 = ( 0; 500;
X2 = ( 0; 500;  .
.
Вычислим градиент искомой целевой функции в точке X2 и составим соответствующую задачу линейного программирования:
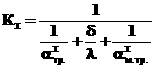
Проверим коэффициенты текущей задачи линейного программирования на чувствительность, используя формулу (1):
 . Ввиду равенства X* = X2, имеем:
. Ввиду равенства X* = X2, имеем:
 X2 является искомым оптимальным вектором, а максимальное значение целевой функции z составляет zmax
= 8350.
X2 является искомым оптимальным вектором, а максимальное значение целевой функции z составляет zmax
= 8350.
Выводы
Использованные в задаче методы позволяют разрешить довольно широкий класс задач нелинейного программирования. Однако, они не являются ниверсальными, в частности, метод линейных комбинаций рассматривает лишь линейные ограничения. В реальной действительности всё далеко не так просто: любая фирма функционирует в конкурентной рыночной среде - задача максимизации прибыли должна учитывать принятие правленческих решений (стратегий), позволяющих предугадать поведение конкурентов.
К тому же, каким бы хорошим не было решение задачи, всегда в реальной жизни необходимо руководствоваться здравым смыслом и трактовать полученные результаты применительно к конкретной ситуации, которая, как известно, всегда несколько отличается от теоретических положений.
Для соответствия полученныха теоретических данных экспериментальным возможно понадобится более сложная структура методов.
Список использованной литературы
1. Таха Х. А. Введение в исследование операций // М.: Вильямс, 2001.
2. Смородинский С. С., Батин Н. В. Оптимизация решений на основе методов и моделей математического программирования // Минск: БГУИР, 2003
3. Степанова М. Д. Проверка статистических гипотез // Минск: БГУИР, 2
4. Волковец А. И., Гуринович А. Б. Теория вероятностей и математическая статистика // Минск: БГУИР, 2003
5. Лутманов С. В. Линейные задачи оптимизации // Пермь: Пермский н-т, 2004