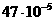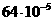Читайте данную работу прЯмо на сайте или скачайте
Оценка безотказной работы технической аппаратуры (задачи)
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ НИВЕРСИТЕТ
им. А.Н.ТУПОЛЕВА
Кафедра КиПМЭА
Курсовая работа
По предмету:
лтехническая эксплуатация
Работу выполнил: Сафин М.Р.
Работу проверил: Толок В.И.
Казань 2004-12-05
Задача 1.
На испытании находится N0 =3570 образцов невосстанавливаемой аппаратуры.
Число отказов êni фиксировалось через интервал êti=70 часов
|
êti, час |
êni |
êti, час |
êni |
êti, час |
êni |
|
Е70 |
89 |
119Е1260 |
22 |
238Е2450 |
81 |
|
7Е140 |
87 |
126Е1330 |
23 |
245Е2520 |
84 |
|
14Е210 |
78 |
133Е1400 |
24 |
252Е2590 |
87 |
|
21Е280 |
75 |
140Е1470 |
24 |
259Е2660 |
90 |
|
28Е350 |
72 |
147Е1540 |
26 |
266Е2730 |
95 |
|
35Е420 |
67 |
154Е1610 |
28 |
273Е2800 |
99 |
|
42Е490 |
64 |
161Е1680 |
29 |
280Е2870 |
101 |
|
49Е560 |
60 |
168Е1750 |
30 |
287Е2940 |
106 |
|
56Е630 |
54 |
175Е1820 |
3 |
294Е3010 |
110 |
|
63Е700 |
43 |
182Е1890 |
35 |
301Е3080 |
121 |
|
70Е770 |
31 |
189Е1960 |
36 |
308Е3150 |
140 |
|
77Е840 |
24 |
196Е2030 |
38 |
315Е3220 |
145 |
|
84Е910 |
22 |
203Е2100 |
48 |
322Е3290 |
149 |
|
910...980 |
23 |
210Е2170 |
59 |
329Е3360 |
160 |
|
98Е1050 |
22 |
217Е2240 |
63 |
336Е3430 |
164 |
|
105Е1120 |
21 |
224Е2310 |
66 |
343Е3500 |
180 |
|
112Е1190 |
22 |
231Е2380 |
69 |
350Е3570 |
189 |
Вычислить значения статистических оценок интенсивности отказов 

 аи вероятности отказов а
аи вероятности отказов а
С 3500 часа до 3570 отказали 182
(189-7=182 т.к. 
Решение:
 агде:
агде: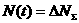 а
а 

 где: К=70(шаг)
где: К=70(шаг)
|
|
|
|
|
|
|
|
|
|
êni |
êni |
êni |
|
89 |
875 |
1557 |
0,975 |
0,755 |
0,564 |
0,025 |
0,245 |
0,436 |
89 |
22 |
81 |
|
176 |
898 |
1641 |
0,951 |
0,749 |
0,541 |
0,049 |
0,251 |
0,459 |
87 |
23 |
84 |
|
254 |
922 |
1728 |
0,929 |
0,742 |
0,516 |
0,071 |
0,258 |
0,484 |
78 |
24 |
87 |
|
329 |
946 |
1818 |
0,908 |
0,736 |
0,491 |
0,092 |
0,264 |
0,509 |
75 |
24 |
90 |
|
401 |
972 |
1913 |
0, |
0,728 |
0,465 |
0,112 |
0,272 |
0,535 |
72 |
26 |
95 |
|
468 |
1 |
2012 |
0,986 |
0,72 |
0,437 |
0,014 |
0,28 |
0,563 |
67 |
28 |
99 |
|
532 |
1029 |
2113 |
0,851 |
0,712 |
0,409 |
0,149 |
0,288 |
0,591 |
64 |
29 |
101 |
|
592 |
1059 |
2219 |
0,835 |
0,704 |
0,379 |
0,165 |
0,296 |
0,621 |
60 |
30 |
106 |
|
646 |
1062 |
2329 |
0,82 |
0,703 |
0,348 |
0,18 |
0,297 |
0,652 |
54 |
3 |
110 |
|
689 |
1097 |
2450 |
0,808 |
0,693 |
0,314 |
0,192 |
0,307 |
0,686 |
43 |
35 |
121 |
|
720 |
1133 |
2590 |
0,799 |
0,683 |
0,275 |
0,201 |
0,317 |
0,725 |
31 |
36 |
140 |
|
744 |
1171 |
2735 |
0,792 |
0,672 |
0,234 |
0,208 |
0,328 |
0,766 |
24 |
38 |
145 |
|
766 |
1219 |
2884 |
0,786 |
0,659 |
0,193 |
0,214 |
0,341 |
0,807 |
22 |
48 |
149 |
|
789 |
1278 |
3044 |
0,779 |
0,643 |
0,148 |
0,221 |
0,357 |
0,852 |
23 |
59 |
160 |
|
811 |
1341 |
3208 |
0,773 |
0,625 |
0,102 |
0,227 |
0,375 |
0,898 |
22 |
63 |
164 |
|
832 |
1407 |
3388 |
0,767 |
0,606 |
0,074 |
0,233 |
0,396 |
0,926 |
21 |
66 |
180 |
|
853 |
1476 |
3577 |
0,762 |
0,587 |
-0,001 |
0,238 |
0,413 |
1,001 |
22 |
69 |
189 |
|
|
|
|
|
|
|
|
3,56 |
0,88 |
3,24 |
3,47 |
0,66 |
1,82 |
|
3,48 |
0,92 |
3,36 |
3,309 |
0,68 |
1,81 |
|
3,12 |
0,96 |
3,48 |
2,898 |
0,71 |
1,79 |
|
3,00 |
0,96 |
3,6 |
2,724 |
0,7 |
1,76 |
|
2,88 |
1,04 |
3,8 |
2,557 |
0,757 |
1,76 |
|
2,68 |
1,1 |
3,96 |
2,64 |
0,792 |
1,73 |
|
2,56 |
1,16 |
4,04 |
2,17 |
0,825 |
1,65 |
|
2,4 |
1,2 |
4,24 |
2,004 |
0,844 |
1,6 |
|
2,16 |
12 |
4,4 |
1,74 |
0,436 |
1,53 |
|
1,72 |
1,4 |
4,84 |
1,38 |
0,97 |
1,51 |
|
1,24 |
1,44 |
5,6 |
0,99 |
0,98 |
1,51 |
|
0,96 |
1,52 |
5,8 |
0,76 |
1,021 |
1,35 |
|
0,88 |
1,92 |
5,96 |
0,69 |
1,26 |
2,03 |
|
0,92 |
2,36 |
6,4 |
0,71 |
1,51 |
0,94 |
|
0,88 |
2,52 |
6,56 |
0,68 |
1,57 |
0,66 |
|
0,84 |
2,64 |
7,2 |
0,64 |
1,59 |
0,53 |
|
0,88 |
2,76 |
7,56 |
0,67 |
1,6 |
-0,007 (0) |
Вывод:
- по ровню 0,7 отказ на 3145 часу
- по ровню 0,3:
для:  ас 2570 часа
(увеличение числа отказов)
ас 2570 часа
(увеличение числа отказов)
 ас 1800 часа (идет старение изделий)
ас 1800 часа (идет старение изделий)


Задача 2.
Используя поток отказов задачи 1, считая закон распределения отказов показательным, вычислить среднее время наработки на отказ для следующих допущений:
) на испытании находилось 
В) на испытании находились только те образцы, которые отказали.
 ачасов
ачасов
Вывод: поскольку все образцы отказали, то среднее время наработки на отказ находившихся на испытании образцов и отказавших образцов равны.
Задача 3.
Используя полученные в задаче 1 показатели надежности, оценить вероятность того, что изделие, проработавшее безотказно в течение 3430 часов не откажет в следующие 70 часов.

Задача 4.
|
êti, час |
Е100 |
10Е200 |
20Е300 |
30Е400 |
40Е500 |
|
êni |
26 |
34 |
29 |
27 |
33 |
|
êti, час |
50Е600 |
60Е700 |
70Е800 |
80Е900 |
90Е1 |
|
êni |
25 |
41 |
39 |
31 |
25 |
 при
N0=50
при
N0=50
|
N= i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0,01 |
0,021 |
0,0138 |
0,0117 |
0,0194 |
0,01 |
0,0455 |
0,035 |
0,063 |
0,01 |
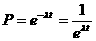 при tнар=400 часов
при tнар=400 часов
|
|
0,994 |
0,79 |
0,94 |
0,75 |
0,6 |
|
êti, час |
0,5 |
2 |
5 |
24 |
240 |


Задача 5.
15 отказов
|
№отк.1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
t,мин |
65 |
54 |
63 |
71 |
46 |
59 |
21 |
88 |
59 |
43 |
49 |
31 |
16 |
73 |
58 |

 (0,8844ч.)
(0,8844ч.) 

|
|
0,75 |
1 |
1,5 |
3 |
0,8844 |
|
|
0,573 |
0,677 |
0,817 |
0,9665 |
0,63 |
Задача 6.
Используя данные задачи 5, определить время восстановления радиостанции с вероятностью 0,7; 0,9; 0,95; 0,98.

|
|
0,3 |
0,1 |
0,05 |
0,02 |
|
|
1,05 |
2,02 |
2,63 |
3,44 |
Задача 7.
Радиотехническое стройство состоит из 4 блоков, отказ любого блока приводит к отказу стройства. Поток отказов являются простейшими и составляют для каждого из блоков:
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
0, |
0,2 |
0,9987 |
0,9985 |
|
|
0,001 |
0,8 |
0,0013 |
0,0015 |


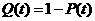
Определить вероятность того, что за два часа работы в стройстве:
1) - не появилось ни одного отказа;
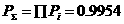
2) - появится хотя бы один отказ:

3) - появится один отказ.

Задача8.

Рассчитать вероятность безотказной работы прибора в течение 30 часов. Структурная схема блока:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
7,4 |
4,9 |
6,5 |
9 |
5,4 |
3,6 |
4,4 |
9 |
|
|
0,978 |
0,9855 |
0,98 |
0,97 |
0,984 |
0,98 |
0,986 |
0,97 |
|
|
0,022 |
0,0145 |
0,02 |
0,03 |
0,016 |
0,02 |
0,014 |
0,03 |



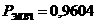


 а
а 


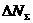


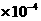








 , 1/ч
, 1/ч