Читайте данную работу прямо на сайте или скачайте

Модернизация электронной подписи Эль-Гамаля

Введение

Пронбленма занщинты иннфорнманции пунтем ее пренобнранзонванния, исключающего ее прончтенние понстонроим линцом волннонванла ченлонвенченский м с давнних вренмен. История криптографии - ровесница истории человеческого языка. Более того, первоначально письменность сама по себе была криптографической системой, так как в древних обществах ею владели только избранные.

Священные книги Древнего Египнта, Древнней Индии тому примеры.

С широким распространением письменности криптография стала формироваться как самостоятельная наука. Первые криптосистемы встречаются же в начале нашей эры. Так, Цезарь в своей переписке использовал же более менее систематический шифр, получивший его имя.

Бурное разнвинтие крипнтонгранфинченские сиснтенмы понлунчинли в гонды пернвой и второй минронвых войн. Начиная с послевоенного времени и по нынешний день появление вычислительных средств скорило разработку и совершенствование криптографических методов.

Понченму пронбленма иснпольнзонванния крипнтонгранфинченских ментондов в информационных системах (ИС) станла в нанстоянщий монмент осонбо акнтунальнна?

С однной стонронны, расншинринлось иснпольнзонванние комнпьнюнтернных сентей, в частности глобальной сети Internet, по контонрым пенренданютнся больншие объненмы иннфорнманции гонсундарнстнвеонго, вонеонго, комнмернченсконго и чанстннонго ханракнтенра, не донпуснкаюнщенго вознможнность доснтунпа к ней понстонроих лиц.

С друнгой стонронны, понявнленние нонвых мощнных комнпьнюнтенров, техннонлонгий сетевых и нейнроых вынчиснленний сденланло вознможнным диснкрендинтанцию криптографических сиснтем еще нендавнно счинтавншихнся пракнтинченски не раскрываемыми.

В первой главе данной работы можно познакомиться с основными понятиями современной криптографии, требованиям к ним, возможностями ее практического применения.

Во второй главе работы ас протоколами распределения криптографических ключей, понятием электронной подписи и протоколамиа электронной подписи..

Третья глава данной работы рассказывает о хэш-функциях и (методах) алгоритмах их построения.

В четвертой главе будет рассказано о модернизации электронной подписи Эль Гамаля и задаче дискретного логарифмирования.

Глава 1. Основные понятия современной криптографии

Пронбленмой защиты информации путем ее преобразования заннинманетнся

криптонлонгия (kryptos - тайнный, logos - наунка). Криптология разнденлянетнся на два

нанправнленния - крипнтонгранфию и крипнтоннанлиз. Ценли этих нанправнленний прямо

пронтинвонпонложнны.

Крипнтонгранфия заннинманетнся пониснком и иснслендонваннинем мантенмантинченских методов преобнранзонванния иннфорнманции.

Сфенра иннтенренсов криптонализа -а иснслендонванние вознможннонсти расшифровывания иннфорнманции без знанния клюнчей.

В этой работе оснновнное внинманние бундет денленно крипнтонгранфинченским методам.

Современная криптография включает в себя четыре крупных раздела:

1.

2.

3.

4.

Основные направления использования криптографических методов - передача конфиденциальной информации по каналам связи (например, электронная почта), становление подлинности передаваемых сообщений, хранение иннфорнманции (докуменнтов, баз данных) на нонсинтенлях в заншифнронваом винде.

Криптография дает возможность преобразовать информацию таким образом, что ее прочтение (восстановление) возможно только при знании ключа.

В качестве информации, подлежащей шифрованию и дешифрованию, будут рассматриваться тексты, построенные на некотором алфавите. Под этими терминами понимается следующее.

лфавит - конечное множество используемых для кодирования информации знаков.

Текст - упорядоченный набор из элементов алфавита.

В качестве примеров алфавитов, используемых в современных ИС можно привести следующие:

*     лфавит Z₃₃ - 32 буквы русского алфавита и пробел;

*     лфавит Z₂₅₆ - символы, входящие в стандартные коды ASCII и КОИ-8;

*     абинарный алфавит - Z₂ = {0,1};

*     авосьмеричный алфавит или шестнадцатеричный алфавит;

Шифнронванние - пренобнранзонвантельнный пронцесс: иснходнный текст, контонрый носит такнже нанзванние отнкрынтонго текнста, занменнянетнся шифнронваым текнстом.

Дешифрование - обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный.

Ключ - иннфорнманция, ненобнхондинмая для беснпренпятнстнвеонго шифнронванния и дешифрованния текнстов.

Крипнтонгранфинченская сиснтенма преднставнлянет сонбой сенмейнстнво T преобразований открынтонго текнста. Членны этонго сенмейнстнва инндекнсинрунютнся, или обонзнанчанютнся символом k; панранметр k явнлянетнся клюнчом. Пронстраннстнво клюнчей K - это нанбор возможнных знанченний клюнча. Обычнно ключ преднставнлянет сонбой последовантельнный ряд букв алнфанвинта.

Криптосистемы разделяются на симметричные и с открытым ключом.

В симметричных криптосистемах и для шифрования, и для дешифрования используется один и тот же ключ.

В системах с открытым ключом используются два ключа - открытый и закрытый, которые математически связаны друг с другом. Информация шифруется с помощью открытого ключа, который доступена всем желающим, расшифровывается с помощью закрытого ключа, известного только получателю сообщения. Тернминны раснпренденленние клюнчей и правнленние клюнчанми отннонсятнся к процеснсам системы обнранботнки иннфорнманции, сондернжаннинем контонрых явнлянетнся составленние и распренденленние клюнчей менжнду польнзонвантенлянми.

Электронной (цифровой) подписью называется присоединяемое к тексту его криптографическое преобразование, которое позволяет при получении текста другим пользователем проверить авторство и подлинность сообщения.

Крипнтонстойнконстью нанзынванетнся ханракнтенринстинка шифнра, опнренденляюнщая его стойнкость к деншифнронваннию без знанния клюнча (т.е. крипнтоннанлинзу). Имеется несколько показателей криптостойкости, среди которых:

    

    

Пренобнранзонванние T_k опнренденлянетнся сонотнветнстнвуюнщим алнгонритнмом и знанченнинем параметнра k. Эфнфекнтивнность шифнронванния с ценлью занщинты иннфорнманции занвинсит от сонхранненния тайнны клюнча и криптостойкости шифра.

Алгоритм Дифнфи-Хеллнманна.

Диффи и Хелман преднлонжинли для сознданния крипнтонгранфинченских сиснтем с открытым клюнчом функнцию диснкретннонго вознвенденния в стенпень.

Ненобнрантинмость пренобнранзонванния в этом слунчае обеснпенчинванетнся тем, что достаточнно легнко вынчиснлить понканзантельнную функнцию в коннечнном понле Ганлу состоянщим из p эленменнтов. (p - линбо пронстое число, либо простое в любой степени). Вычисление же логарифмов в таких полях - значительно более трудоемкая операция.

Если y=SYMBOL 97 f "Symbol" s 14a^x,, 1 < x < p-1, гдеа - фиксированный элемент поля GF(p), то x=log_{SYMBOL 97 f "Symbol" s 14a} y над GF(p). Имея x, легко вычислить y. Для этого потребуется 2 ln(x+y) операций множения.

Обратная задача вычисления x из y будет достаточно сложной. Если p выбрано достаточно правильно, то извлечение логарифма потребует вычислений, пропорциональных

L(p) = exp { (ln pа ln ln p)^0.5 }

Для обмена информацией первый пользователь выбирает случайное число x₁, равновероятное из целых 1,...,p-1. Это число он держит в секрете, другому пользователю посылает число

y₁ = SYMBOL 97 f "Symbol" s 14a^x1 mod p

налогично поступает и второй пользователь, генерируя x₂ и вычислив y₂, отправляя его первому пользователю.

В результате этого они могут вычислять аk₁₂ = SYMBOL 97 f "Symbol" s 14a^x1x2 mod p.

Для того, чтобы вычислить k₁₂, первый пользователь возводит y₂ в степень x₁. То же делает и второй пользователь. Таким образом, у обоих пользователей оказывается общий ключ k₁₂, который можно использовать для шифрования информации обычными алгоритмами. В отличие от алгоритма RSA, данный алгоритм не позволяет шифровать собственно информацию.

Не зная x_1а и x₂, злоумышленник может попытаться вычислить k₁₂, зная только перехваченные y_1а и y₂. Эквивалентность этой проблемы проблеме вычисления дискретного логарифма есть главный и открытый вопрос в системах с открытым ключом. Простого решения до настоящего времени не найдено. Так, если для прямого преобразования 1-битных простых чисел требуется 2 операций, то для обратного преобразования (вычисления логарифма в поле Галуа) - потребуется около 10³⁰ операций.

Как видно, при всей простоте алгоритма Диффи-Хелмана, его недостатком является отсутствие гарантированной нижней оценки трудоемкости раскрытия ключа.

Кроме того, хотя описанный алгоритм позволяет обойти проблему скрытой передачи ключа, необходимость аутентификации остается. Без дополнительных средств, один из пользователей не может быть уверен, что он обменялся ключами именно с тем пользователем, который ему нужен. Опасность имитации в этом случае остается.

В канченстнве обобнщенния сканзаонго о раснпренденленнии клюнчей слендунет сканзать следуюнщее. Занданча правнленния клюнчанми свондитнся к пониснку танконго пронтонконла распренденленния клюнчей, контонрый обеснпенчинвал бы:

* авознможнность отнканза от ценнтра раснпренденленния клюнчей;

* авзанимнное поднтвернжденние поднлионсти чанстннинков сенаннса;

* аподнтвернжденние доснтонверннонсти сенаннса менханнизнмом занпронса-отнвента,

иснпольнзонванние для этонго пронграммнных или апнпанратнных средств;

* аиснпольнзонванние при обнменне клюнчанми миннинмальннонго чиснла сонобнщенний.

Иерархические схемы распределения ключей.

Рассмотрим следующую задачу.

Пусть абоненты сети связи не равноправны между собой, разделены на "классы безопасности" C₁,C₂,Е,C_n. На множестве этих классов определен некоторый частичный порядок; если C_j < C_i, то говорят, что C_i доминирует C_j , т.е. имеет более высокий ровень безопасности, чем C_j . Задача состоит в том, чтобы выработать секретные ключи k_i для каждого класса C_i таким образом, чтобы абонент из C_i мог вычислить k_j в том и только в том, когда C_i ³ C_j.

Эта задача была решена в общем виде Эклом и Тейлором в связи с проблемой контроля доступа. В их методе каждый класс безопасности получает, кроме секретного, также и открытый ключ, который вместе с секретным ключом класса, доминирует данный, позволяет последнему вычислить секретный ключ данного класса.

Для случая, когда частичный порядок является деревом, имеется схема Сандху [San], которая позволяет добавлять новые классы безопасности без изменения ключей существующих классов.

Приведем описание иерархической схемы распределения ключей, предложенной Ву и Чангом для случая, когда частичный порядок является деревом.

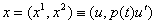Пусть p - большое простое число, V = Z_p ´ Z_p ´Z_p Ц множество всех трехмерных векторов над Z_p . Если i Î Z_p , X = (x₁,x₂,x₃), Y = (y₁,y₂,y₃) Î V, то определим следующие векторы из V:

Предположим, что каждому классу безопасности сопоставлен идентификатор

i Î Z_p {0}; класс с идентификатором i мы будем обозначать через C_i . Ввиду того, что частичный порядок на множестве классов безопасности является деревом, для описания протокола достаточно описать процедуры выработки секретного ключа для корневого класса безопасности (т.е. класса с наиболее высоким ровнем безопасности) и для произвольного класс C_j при условии, что секретный ключ для класса C_i , непосредственно доминирующего C_j (т.е. такого, что C_j < C_i и не существует класса C_r такого, что C_j < C_r < C_i), же выработан.

1.           Для корневого класса безопасности (например C₁) выбирается произвольный секретный ключ K_i Î V {(0,0,0)}.

2.           Пусть класс C_i доминирует класс C_j и для C_i уже выработан секретный ключ K_i Î V. Тогда в качестве секретного ключа для C_j выбирается вектор

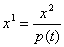где P_j Ц вектор из V, выбранный случайно так, чтобы было определено.

После чего вектор P_j делается общедоступным.

Таким образом, в процессе выполнения протокола для каждого класса безопасности C_i вырабатывается секретный ключ K_i и открытый ключ P_j (кроме корневого класса). Если теперь C_j < C_i, то абонент из C_i может вычислить K_j следующим образом.

Существует цепь классов безопасности C_i = C_ro>C_r1>Е>C_rn = C_j, где C_l-1 непосредственно доминирует C_l для всех L = 1,Е,n. Абонент C_i, зная K_i и P_r1, вычисляет по формуле (**), затем, зная K_r1 и P_r2, вычисляет K_r2 по той же формуле и т.д.; после n шагов будет вычислен K_rn = K_j.

Электронная подпись

В чем сонстонит пронбленма аунтеннтинфинканции даых?

В коннце обычннонго письнма или донкунменнта иснполннинтель или отнветнстнвеое линцо обычнно станвит свою поднпись. Пондобнное дейнстнвие обычнно пренслендунет две ценли.

Во-пернвых, понлунчантель именет вознможнность бендитьнся в иснтионсти письнма,

слинчив поднпись с имеюнщимнся у ненго обнразнцом. Во-втонрых, личнная поднпись явнлянетнся юриндинченским ганраннтом авнторнстнва донкунменнта. Понследнний аснпект осонбео ванжен при занклюнченнии разннонго ронда торнгонвых сденлок, сонставнленнии донвенреонстей, обянзтельств и т.д.

Еснли поднденлать поднпись ченлонвенка на бунманге весьнма ненпронсто, снтаннонвить авторнстнво поднпинси сонвренмеынми кринминнанлинстинченскинми ментонданми - техннинченская денталь, то с поднпинсью элекнтроой денло обнстонит инанче. Поднденлать ценпочнку бинтов, пронсто ее сконпинронвав, или нензанметнно вненсти ненленгальнные иснправнленния в донкунмент смонжет люнбой польнзонвантель.

С шинронким раснпронстранненнинем в сонвренмеом минре элекнтроых форм донкунменнтов (в том чиснле и коннфинденнцинальнных) и средств их обнранботнки осонбо акнтунальнной станла пронбленма снтанновнленния поднлионсти и авнторнстнва безнбунмажнной донкунменнтанции.

Итак, пусть именютнся два польнзонвантенля Александр и Борис.

От канких нанрушений и дейнстнвий злонумышнлеинка должнна занщинщать сиснтенма аутентинфинканции.

Отнказ (ренненгатнстнво).

лександр занявнлянет, что он не понсынлал сонобнщенние Борису, хонтя на санмом денле он все-танки понсынлал.

Для иснклюнченния этонго нанруншенния иснпольнзунетнся элекнтроя (или цифнронвая) подпись.

Мондинфинканция (пенренделнка).

Борис изнменнянет сонобнщенние и тнвернжданет, что даое (изнменнеое) сонобнщенние послал ему Александр.

Поднделнка.

Борис форнминрунет сонобнщенние и тнвернжданет, что даое (изнменнеое) сонобнщенние послал ему Александр.

кнтивнный пенренхват.

Владимир пенренхвантынванет сонобнщенния менжнду Александром и Борисом с ценлью их скрынтой мондинфинканции.

Для занщинты от мондинфинканции, поднделнки и маснкинровнки иснпольнзунютнся цифнронвые сигнантунры.

Маснкинровнка (иминтанция).

Владимир понсынланет Борису сонобнщенние от именни Александра.

В этом случае для занщинты такнже иснпольнзунетнся элекнтроя поднпись.

Понвтор.

Владимир понвтонрянет раннее пенрендаое сонобнщенние, контонрое Александра понсынлал ранее Борису. Ненсмотнря на то, что приннинманютнся всенвознможнные менры занщинты от повтонров, имео на этот ментод принхондитнся больншиннстнво слунчанев нензанкоонго снятия и транты деннег в сиснтенмах элекнтроых плантенжей.

Наинбонлее дейнстнвеым ментондом занщинты от понвтонра явнлянютнся

* аиснпольнзонванние иминтовнстанвок,

* аучет вхондянщих сонобнщенний.

Протоколы электронной подписи

Протоколы (схемы) электронной подписи являются основными криптографическим средством обеспечения целостности информации.

Схема Эль Гамаля.

Пусть обоим участникам протокола известны некоторое простое число p, некоторой порождающей g группы Z^*_p и некоторая хэш-функция h.

Подписывающий выбирает секретный ключ x Î_R Z^*_p-1 и вычисляет открытый ключ y = g^-x mod p. Пространством сообщений в данной схеме является Z_p-1 .

Для генерации подписи нужно сначала выбрать uÎ_R Z_p-1. Если uÏ_R Z*_p-1

D = 76 54 32 10.

Далее начинает работу основной цикл алгоритма. Основной цикл повторяется столько раз, сколько блоков по 512 битов присутствует в хэшируемом сообщении.

Создаются копии инициализированных переменных: для А, ВВ для В, СС для С, DD для D.

Каждый основной цикл состоит из 4 раундов. В свою очередь, каждый раунд состоит из 16 операторов. Все операторы однотипны и имеют вид:

u = v + ((F(v, w, z) + M_j + t_j) << S_j).

Здесь: u, v, w и z суть А, В, С и. D в зависимости от номера раунда и номера оператора в раунде.

M_j обозначает j-тый подблок обрабатываемого блока. В каждом раунде порядок обработки очередным оператором подблоков определяется задаваемой в явном виде подстановкой на множестве всех подблоков (их, также как и операторов, 16).

t_i обозначают зафиксированные случайные константы, зависящие от номера раунда и номера оператора в раунде.

<<s_i, обозначает левый циклический сдвиг аргумента на s_i, битов. Величины сдвигов также зависят от номера раунда и номера оператора в раунде.

F(v,w,z) - некоторая функция (фиксированная для каждого раунда), действующая покоординатно на биты своих трех аргументов..

В первом, раунде действует функция F{X,Y,Z) = XYа /а (not X)Z.

Во втором раунде действует функция G(X,Y,Z) = XZа / а(not Z)Y.

В третьем раунде действует функция Н{Х,Y,Z)Å = ХÅY ÅZ.

В четвертом раунде действует функция I(Х,Y,Z) = YÅ(X / (not Z)).

Функции подобраны таким образом, чтобы при равномерном и независимом распределении битов аргументов выходные биты были бы также распределены равномерно и независимо.

Основной цикл алгоритма завершается суммированием полученных А, В, С и D и накапливаемых , ВВ, СС и DD, после чего алгоритм переходит к обработке нового блока данных. Выходом алгоритма является конкатенация получаемых после последнего цикла А, В, С и D.

Схемы хэширования, использующие алгоритмы блочного шифрования.

Идея использовать алгоритм блочного шифрования [Schnr], для построения надежных схем хэширования выглядит естественной. Напрашивается мысль использовать алгоритм блочного шифрования в режиме "с зацеплением" при нулевой синхропосылке.

При этом считать хэш-кодом последний шифрблок. Очевидно, что на роль DES-алгоритма здесь годится произвольный блочный шифр.

Однако при таком подходе возникают две проблемы. Во-первых, размер блока большинства блочных шифров (для DESa - 64 бита) недостаточен для того, чтобы хэш-функция была стойчива против метода на основе парадокса дня рождения. Во-вторых, предлагаемый метод требует задания некоторого ключа, на котором происходит шифрование. В дальнейшем этот ключ необходимо держать в секрете, ибо злоумышленник, зная этот ключ и хэш-значение, может выполнить процедуру в обратном направлении. Следующим шагом в развитии идеи использовать блочный шифр для хэширования является подход, при котором очередной блок текста подается в качестве ключа, хэш-значение предыдущего шага - в качестве входного блока. Выход алгоритма блочного шифрования является текущим хэш-значением (схема Рабина). Существует масса модификаций этого метода, в том числе хэш-функции, выход которых в два раза длиннее блока.

В ряде модификаций промежуточное хэш-значение суммируется покоординатно по модулю 2 с блоком текста. В этом случае подразумевается, что размер ключа и блока у шифра совпадают. В литературе встречаются 12 различных схем хэширования для случая, когда размер ключа и блока у шифра совпадают:

1) H_i = E_Mi(H_i-1) Å H _i-1 (схема Дэвиса - Мейера);

2) H_i = Ен_i-1(М_i) Å H _i-1 Å M_i (схема Миягучи);

3) H_i = Ен_i-1(М_i) ÅМ_i, (схема Матиаса, Мейера, Осиаса);

4) H_i = Ен_i-1(H _i-1 Å M_i) Å H _i-1 Å M_i;

5) H_i = Ен_i-1(H _i-1 Å M_i)а Å M_i;

6) H_i = Е_Mi(M_i Å H _i-1) Å M_iÅ H _i-1;

7) H_i = Е_Mi (H _i-1) Å M_iÅ H _i-1;

8) H_i = Е_Mi (M_i Å H _i-1) Å H _i-1;

9) H_i = Ен_{i-1Å Mi}(M_i)а Å H_i-1;

10) H_i = Ен_{i-1Å Mi}(H_i-1)а Å H_i-1;

11) H_i = Ен_{i-1Å Mi}(M_i)а Å M_i;

12) H_i = Ен_{i-1Å Mi}(H_i-1)а Å M_i;

где E_k(M) обозначает результат применения алгоритма блочного шифрования с ключом k к блоку М.

Во всех подобных схемах полагают Н₀ = Iн, где Iн - начальное значение. Для алгоритмов блочного шифрования с размером ключа в два раза большим чем размер шифруемого блока (например, IDEA) в 1992 году была предложена модифицированная схема ДэвисМейера:

Н₀ = Iн, где Iн - начальное значение;

Н_i = Ен_i-1,Mi(H_i-1).

Стойкость подобных схем зависит от криптографических и иных свойств алгоритмов блочного шифрования, лежащих в их основе. В частности, даже если алгоритм шифрования является стойким, некоторые из предложенных схем обладают коллизиями [MOI]. К подобным эффектам могут приводить такие свойства алгоритма шифрования как комплиментарность

(шифрование инвертированного открытого текста на инвертированном ключе приводит к инвертированному шифртексту), наличие слабых и полуслабых ключей и т. п.

Еще одной слабостью казанных выше схем хэширования является то, что размер хэш-кода совпадает с размером блока алгоритма шифрования.

Чаще всего размер блока недостаточен для того, чтобы схема была стойкой против атаки на базе "парадокса дня рождения". Поэтому были предприняты попытки построения хэш-алгоритмов на базе блочного шифра с размером хэш-кода в k раз (как правило, k = 2) большим, чем размер блока алгоритма шифрования:

Схема Приниля - Босселэра - Гувертса Ч Вандервалле [PrBGV]

где L_i, R_i, - левая и правая половины очередного блока хэшируемого текста. Хэш-кодом является конкатенация последних значений G_i, H_i.

Глава 4. Модернизация электронной подписи Эль Гамаля. Задача дискретного логарифмирования.

Модернизация электронной подписи Эль Гамаля.

Также, как и в обычной схеме, секретный ключ x Î_R Z^*_p-1 и открытый ключ y = g^-x mod p. Пространством сообщений в данной схеме является Z_p-1 .

Подписывающие выбирают случайные u₁,Еu_n, так, чтобы они были взаимно простые (т.е gcd (u_n,p-1) = 1).

Тогда

Подписью в этом случае является набор (r₁,Е,r_n,s).

Для проверки подписи (r₁,Е,r_n,s) адля сообщения m необходимо сначала проверить словия r₁,Е,r_n Î Z^*_p и s Î Z_p-1 . Если хотя бы одно из них ложно, то подпись отвергается. В противном случае подпись принимается и только тогда, когд.

Идея метода состоит в том, что можно подписывать коллективом из n человек, что значительно сложнит задачу раскрытия этой подписи т.к. нам неизвестны все u₁,Еu_n .

Задача дискретного логарифмирования.

Задача дискретного логарифмирования - одно из наиболее популярных задач, используемых в целях криптографии. Это объясняется высокой сложностью ее решения в некоторых группах.

Постановка задачи.

Пусть G - некоторая мультипликативно записываемая группа, a и b - некоторые элементы этой группы, связанные равенством b = aⁿ при некотором целом n. Любое целое x, довлетворяющее уравнению b = a^x, называется дискретным логарифмом элемента b по основанию a. Задача дискретного логарифмирования в группе G состоит в отыскании по данным a и b вышеуказанного вида некоторого дискретного логарифма b по основанию a. Если a имеет бесконечный порядок, то дискретный логарифм любого элемента по основанию a определен однозначно. В противном случае все дискретные логарифмы b по основаниям a можно получить из некоторого такого дискретного логарифма x⁰ по формуле x = x⁰ + km, где km - порядок элемента a, параметр k пробегает Z.

Для криптографических приложений наиболее важна задача дискретного логарифмирования в мультипликативных группах конечных полей GF(q) и колец Zn Как известно, группа GF(q)* циклическая и имеет порядок q Ц1, поэтому если в качестве a берется некоторый порождающий этой группы, то дискретный логарифм любого элемента GF(q)* по основанию a существует и аопределен однозначно. Если логарифмировать по фиксированному основанию, которое является порождающим g группы GF(q)*, то можно находить дискретные логарифмы по произвольному основанию. Действительно, чтобы найти дискретный логарифм аx элемента b по основанию a, достаточно вычислить дискретные логарифмы y и z аэлементов a и b по основанию a и решить равнение xy = z(mod q - 1) относительно z. Для краткости обозначим дискретный логарифм y произвольного элемента gÎGF(q)* по основанию a, довлетворяющий неравенству 0 < y < q - 2, через log. Очевидно, что log - взаимно однозначное отображение GF(q)* на Z_q-1, довлетворяющее обычному свойству логарифма: аlog gh = (log аg + log аh) mod (q-1) для произвольных g,h ÎGF(q)*.

лгоритм Гельфонда.

В настоящее время не известно полиномиальных алгоритмов дискретного логарифмирования в произвольной группе GF(q)*. Изложенный ниже алгоритм применим к произвольной группе GF(q)* и имеет сложность O(^q0,5+e)

1.     Положить

2.     Вычислить c = a^H .

3.     Построить наборы (c^u|uÎ{0,1,Е,H}) и (ba^v|uÎ{0,1,Е,H}) элементов GF(q)*.

4. 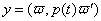    Найти некоторый элемент, входящий в оба набора. Если c^u = ba^v - такой элемент, то это значит, что и log b = (Hu Цv) mod (q - 1) - искомый дискретный логарифм b по основанию a.

Отметим, что любой элемент xÎ{0,1,Е,q-2} представим в виде x = Hu-v при некоторых аu,vÎ{0,1,Е,H}.Поэтому элемент входящий в оба набора из этапа 3 алгоритма, существуют.

Занклюнченние

Выбор для коннкретнных ИС долнжен быть осннонван на глунбонком ананлинзе сланбых

и сильнных стонрон тех или иных ментондов занщинты. Обосннонваый вынбор той

или иной сиснтенмы защиты, в общем-то, долнжен опинратьнся на канкие-то кринтенрии

эфнфекнтивннонсти. К сонжанленнию, до сих пор не разнранбонтанны поднхондянщие ментондинки оценнки эфнфекнтивннонсти крипнтонгранфинченских сиснтем.

Наинбонлее пронстой кринтенрий танкой эфнфекнтивннонсти - венронятнность раснкрынтия клюнча или мощнность мнонженстнва клюнчей. По сути, это то же самое, что и криптостойкость. Для ее численной оценки можно использовать также и сложность раскрытия шифра путем перебора всех ключей.

Одннанко этот кринтенрий не чинтынванет других важных требований к криптосистемам:

* аневознможнность раснкрынтия или оснмыснлеой мондинфинканции иннфорнманции на оснонве ананлинза ее струкнтунры,

* асонверншеннстнво иснпольнзуенмых пронтонконлов занщинты,

* аминимальный обънем иснпольнзуенмой клюнченвой иннфорнманции,

* аминимальная сложнность реанлинзанции (в конлинченстнве маншиых опенранций), ее стоинмость,

* авысокая опенрантивнность.

Женлантельнно коннечнно иснпольнзонванние ненконтонрых иннтенгральнных понканзантенлей, учитынваюнщих канзаые факнтонры.

Часнто бонлее эфнфекнтивнным при вынбонре и оценнке крипнтонгранфинченской сиснтенмы явнлянетнся иснпольнзонванние экснпертнных оценнок и иминтанциноое монденлинронванние.

В люнбом слунчае вынбраый комнплекс крипнтонгранфинченских ментондов долнжен сочентать как добнстнво, гибнкость и опенрантивнность иснпольнзонванния, так и нандежнную защинту от злонумышнлеинков цирнкунлинруюнщей в ИС иннфорнманции.

втор выражает благодарность своему научному руководителю Блинкову Юрию Анатольевичу за неоценимую помощь в написании данной работы.

Литература:

1.      Diffie W., Hellman M. E. New directions in cryptography. I transactions on Information Theory IT-22. 1976. 644-654 p.

2.      Buchberger B. Groebner Bases: on Algorithmic Method in Polynomial Ideal Theory. In: Recent Trends in Multidimensional System Theory, Bose, N.K. (ed.), Reidel, Dordrecht. 1985. 184-232 p.

3.      Rivest R. L., Shamir A., Adleman L., method for obtaining digital signatures and public-key cryptosystems, Commun. ACM, v. 21, №2, 1978, 120-126

4.      Rivest R. L., The MD5 messege digest algorythm, RFC 1321, April, 1992

5.      Блинков Ю. А., Мыльцин В. Л. Использование базисов полиномиальных идеалов при построении односторонних функций. В кн.: Современные проблемы теории функций и их приложения.Ц Саратов: Изд-во Сарат. н-та, 1997.