Кремний, полученный с использованием "геттерирования" расплава

Чакоэффициент распределения, значительно отлинчающийся от единицы;

Чаэффективное изменение коэффициента распреденления даляемых примесей;

Чаотсутствие вредного влияния атомов "геттера" на свойства полупроводника.

Использование в качестве геттера водорода, преднложенное Декоком, не нашло применения в промышнленности, так как водород в процессе отжига даляется из кристалла, вновь освобождая кислород и оставляя после себя напряженные частки кристаллической реншетки.

Добавление в кремний изоморфных примесей (Ge, Pb, Sn)асказывается лишь на кинетике образования термодоноров, при этом сохраняется зависимость их поведения от температуры.

Легирование металлами, изобарный потенциал реакнции окисления которых больше, чем изобарный потеннциал окисления кремния при температуре его плавления, дает возможность связывать кислород и порождаемые им термодефекты. Для этой цели могут быть выбраны примеси, образующие с кислородом более химически и термически стойкие оксиды, чемаSi0^, которыеак тому же электронейтральны в кремнии. Танкими примесями являются щелочноземельные металлы(Mg,Са, Sr,Ва), электрически нейтральные вследствие образования с кремнием полупроводниконвых соединений с ковалентной связью [1,2], и перенходные металлы IV группы(Ti, Zr, Hf), нейтральные по причине сходства строения электронных оболочек их атомов с атомами кремния и также образующие стехиометрические фазы с кремнием. Экспериментальные даые показывают, что при добавлении этих металлов в расплав кислород связывается в жидком кремнии в прочные комплексы, содержащие атомы кремния и кислорода, коэффициент распределения которых гораздо меньше, чем у кислорода, который не связан в комплексы. В результате введения примесейа-геттеров содержание кислорода в выращенных методом Чохральского монокристаллах может быть снижено до 2-10^ 7 смЗ.

Характер распределения Ti, Zr и Hf в монокристалнлах вдоль оси роста аналогичен наблюдавшемуся ранее для щелочноземельных металлов в германии и кремнии, также для примеси хрома в арсениде галлия. Методами химико-спектрального и активационного анализов, методом радиоктивных индикаторов (для циркония и гафния) показано, что в начальной части формируется концентрационный профиль со снижением концентранции, затем переходная область, за которой следует обнласть нарастания концентрации вплоть до выпадения второй фазы. Распределение примесей-геттеров, а также ровень их концентрации в твердой фазе свидетельствунет о том, что их взаимодействие с кислородом происхондит в расплаве с последующим распределением атомов металла, связанного и не связанного с кислородом, с различными коэффициентами сегрегации. Более высонкая концентрация примеси в начале слитка по сравненнию со средней его частью противоречит диаграммам состояния кремний-титан (цирконий, гафний), имеюнщим эвтектический переход, соответственно которому элементы IV группы должны иметь коэффициент раснпределения меньше единицы. Отсутствие зависимости характера распределения от словий -перемешивания расплава подтверждает данные о взаимодействии применсей с кислородом. Следствием такого взаимодействия является различное поведение растворенного металла при кристаллизации кремния. Образуя комплексы, сонответствующие соединениям с высокой температурой плавления и прочными химическими связями, примесь металлIV-Bаможет иметь коэффициент распределения больше единицы. Коэффициенты распределения титана, циркония и гафния, не связанных с кислородом, меньше единицы, и эти металлы оттесняются в конечную часть слитка. Снижение содержания кислорода в монокринсталлах, выращенных методом Чохральского с добавнкой геттера, по сравнению с обычными монокристалнлами подтверждает факт взаимодействия этих примесей в расплаве. Источником обнаруженного оптическикнтивного кислорода, по-видимому, служит тигель(Si0,).

Физическая модель процесса

внутреннего геттерированияв кремниевой

технологии.

Как известно, металлические примеси Au, Fe, Ni, Си и другие приводят к возникновению генерационно-рекомбинационных центров в активных областях приборов на основе кремния, что в свою очередь вызывает деградацию свойств приборов. Совокупность технологических приемов, позвонляющих снизить концентрацию таких центров, локализуя их вблизи преципитатов Si0x (xw2), расположенных вдали от активных областей принборов, называется методом внутреннего геттерирования (ВГ)..

По технологии ВГ накоплен обширный факнтический материал, однако физические принципы его механизма в настоящее время окончательнно не установлены [1, 2). Широкое распространнение, например, получили представления о том, что центрами геттерирования являются дислонкации и дефекты паковки, возникающие вследнствие релаксации пругих полей и пересыщения по межузельному кремнию в процессе преципинтации кислорода при Г>700

Комплексы примесь-точечный дефект и их неоднородное распределение вблизи центра гетгерировання

Принципиальное отличие пругого взаимондействия примеси с дислокацией от взаимодейнствия со сферическим геттером проявляется в том, что пругое поле последнего характеризунется чисто сдвиговой деформацией и энергия пнругого взаимодействия равна нулю :

где К Ч модуль всестороннего сжатия материанла среды, Wo - изменение объема, обусловлеое примесным атомом, eii Чдилатация пругого поля центра. Поэтому в словиях отсутствия ди-латацнонного взаимодействия и наличия пересынщения по собственным дефектам дальнодейст-вующий механизм пругого взаимодействия монжет быть реализован взаимодействием диполь-ного типа. Дипольные свойства примесного атонма могут быть реализованы в случае образованния комплекса из двух точечных дефектов: атом примесиЧсобственный точечный дефект или атом примесиЧатом другой примеси.

Количественной мерой взаимодействия компнлекса точечных дефектов с пругим полем центра дилатации является тетрагональность поля пнругих искажений, создаваемых комплексом. В рамках континуальной теории упругости энергия точечного дефекта в поле eii задается выранжением:

Тензор Wij, называемый тензором объемных денформаций, полностью характеризует пругие свойства точечного дефекта. Для пругого дипонля с осевой симметрией он имеет вид :

ni и nj - направляющие косинусы оси симметнрии диполя.

Для последовательного.количественного опинсания образования примесных сегрегаций вблизи центра геттерирования необходимо знать панраметры Wo и W1, характеризующие отдельный комплекс и определить раснпределение таких комплексов в пространстве, окружающем центр геттерирования. Расчеты характеристик комплекса проводились методом молекулярной статики. За основу был принят так называемый метод флекс-1 (метод гибкой гранницы с перекрывающимися областями). Кринсталл разбивается на три области. Область 1, непосредственно окружающая кристалл, рассматнривается как дискретная. В этой сильно исканженной области координаты атомов учитываютнся индивидуально, энергия рассчитывается с помощью межатомного потенциала. Область 3, наиболее даленная от дефекта, представляется как пругий континуум. Вклад этой области в общую энергию системы определяется решением равнений теории пругости, т.е. величинами W0 и W1 и пругими постоянными среды. Область 2 является промежуточной. Координаты атомов в этой области определяются коллективно также соответствии с теорией пругости, вклад в энергию системы - с помощью межатомного потенциала. В ходе расчета минимизируется полная энергия системы, являющаяся функцией координат атомов и двух переменных Wo и W1, характеризующих дальнодействующее поле денфекта. Решение этой вариационной задачи и дает искомые величины.

Расчеты проводились для моно- и дивакансии с межатомным потенциалом ПлишкинЧ Подчиненова. Область 1 содержала 320 атомов в случае моновакансии и 319 атомов в случае дивакаисии, область 2 содержала 1280 атомов. Дивакансия состояла из двух вакансий в полонжениях (0,0,0) и (1/2, 1/2,0). Результаты расчентов приведены в таблице.

Результмы расчетов компонент тензора объемных деформаций для моно- и днвакансии.

Из таблицы видно, что при образовании компнлекса из двух точечных дефектов, каждый из которых создает в среде сферически симметричнное поле пругих искажений, получается дефект дипольного типа. Кроме того, при этом имеет менсто нарушение аддитивности изменения объема, вызванного дефектами.

Равновесное распределение диполей в пругом поле геттера задается соотношением:

где (Со - концентрация диполей вдали от центнра. Энергия диполя в поле центра в соответстнвии с (1) определяется выражением

где эффективная поляризация дипольного облака 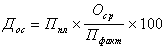определяется как

Величина -g, характеризующая поля центра, явнляется комбинацией пругих постоянных среды и включения, также размера включения.

При проведении расчетов по формулам (2)Ч(5) температура, параметры g и W1 варьинровались с целью изучения их влияния на пронцесс геттерирования. Результаты численного монделирования представлены на рис. 1 и 2. Поканзаны распределения концентрации диполей и понляризации вблизи преципитата радиуса rp для двух случаев, отличающихся знаком пругого поля преципитата. Анализ полученных данных позволяет становить, что независимо от знака пругого поля преципитата имеет место обогащенние диполями пространства вблизи преципинтата.

Рис. 1. Распределение динполей (а) и их поляринзации (б) вблизи сферинческого преципитата с отрицательным объемным несоответствиема Ч0.005.

Рис. 2. Распределение динполей (6) и их поляризация (б) вблизи сфериченского преципитата с положительным объемным несоответствием -0.005.

Диффузионная модель процесса ВГ.

Для рассмотрения кинетики образования равнновесного распределения примеси вокруг прецинпитата запишем. равнение диффузии в виде

- где j вектор плотности потока частица определяется выражением

После подстановки и перехода к сферическим координатам равнение (9) принимает вид:

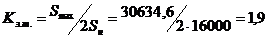
Уравнение (6) совместно с (3) и с соответстнвующими начальными и граничными словиями описывает эволюцию поля концентраций примеснных комплексов С(r), а при tо¥ - равновеснное состояние. В случае ограниченного числа частиц граничными условиями являются: на внешней поверхности j=0, на внутренней границе раздела SiЧSi02, j=VsC, где VsЧ коэффициент поверхностного массопереноса границы раздела кремнийЧокисел. Переходя в равнении (6) к безразмерным переменным :

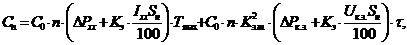
получим :

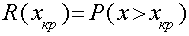а(7)

Результаты численного решения равненния (7) показали, что при больших временах равновесное распределение является предельным для кинетических распределений. Для количестнвенного представления эффективности процесса ВГ на рис. 3 представлена величина h-доля принмеси, геттерированной на преципитате, как функнция безразмерного времени. Кривые 1 и 2 описынвают эффективность процесса ВГ соответствео с четом и без чета упругого взаимодейстнвия. Параметр g соответствует здесь относительнному линейному несоответствию включения и полости в матрице, в которую он вставлен, равнонму 0,005, что типично для кислородного преципинтата в кремнии, выращенном по методу Чохральского. Из рисунка видно, что дополнительный вклад геттерирования, вследствие пругого взаинмодействия сопоставим с величиной геттерированния в отсутствие пругого взаимодействия. При этом процесс ВГ при пругом взаимодействии протекает быстрее.

Рис. 3. Доля геттерированных примесных атомов как функция времени в процентах к их полному числу при начальной коннцентрации (Со=10^-8): 1 - с четом взаимодейнствия примесный комплекс-геттер.

2 - без чета взаинмодействия

Развитая модель формирования атмосфер и геттерирования примесных атомов дипольного типа вблизи сферического преципитата показынвает, что в словиях формирования комплексов примесный атом - точечный дефект кислороднные преципитаты могут служить центрами коннденсации примесных атомов. Если на поверхности преципитата происходит распад комплекса, при котором на ней осаждается атом примеси, то для поддержания равновесного значения концентранции потребуется диффузионно-дрейфовый поднвод новых комплексов. Таким образом, в слонвиях- образования подвижных комплексов принмесный атомЧточечный дефект вдали от прецинпитата и их распада вблизи его развитая модель дает объяснение механизма геттерирования, конторый не имеет ограничения по пересыщению и служит лдрейфовым насосом, обеспечиваюнщим меньшение концентрации примеси в объеме кристалла.

анализ результатов расчетов позволяет вынделить следующие моменты, определяющие свойнства процессов ВГ.

n эффективность геттерирования является функцией температуры, причем существует опнтимальная температура для максимальной эфнфективности этого механизма геттерирования;

n агеттер (преципитат SiO2) действует не только как сток для примесей, но и как источник междоузлий Si, которые активируют процесс ВГ;

n собственные междоузлия кремния, инжекнтируемые растущим преципитатом в объем кринсталла, взаимодействуют с геттерируемыми атонмами, и напряжения влияют на величение дрейфового потока.