Читайте данную работу прямо на сайте или скачайте

История открытия комплексных чисел

Реферат

на тему:

История открытия комплексных чисел.

Выполнили ченики 10 класса

Савинской средней

Школы №1

Сметанин Илья и

Лихачёв Вячеслав.

План:

1. Понятие о комплексном числе.

) Почему появились?

б) Алгебраическая форма комплексного числа.

2. Из истории.

3. Заключение.

4. Список используемой литературы.

1. Понятие о комплексном числе.

Почему появились? Процесс расширения понятий числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами самой математики. Сначала для счёта предметов использовались натуральные числа. Затем необходимость выполнения деления привела к понятию дробных положительных чисел; далее, необходимость выполнения вычитания - к понятиям нуля и отрицательных чисел; наконец, необходимость извлечения корней из положительных чисел - к понятию иррациональных чисел. Все перечисленные операции выполнимы на множестве действительных чисел. Однако остались и невыполнимые на этом множестве операции, например извлечение квадратного корня из отрицательного числа. Значит, имеется потребность в дальнейшем расширении понятий числа, в появлении новых чисел, отличных от действительных.

Геометрически действительные числа изображаются точками на координатной прямой : каждому числу соответствует одна точка прямой (лобраз действительного числа). Координатная прямая сплошь заполнена образами действительных чисел, т. е. на ней нет места для новых чисел. Возникло предположение о том, что геометрические образы новых чисел нужно искать не на прямой, на плоскости.

Комплексным числом называется всякая порядоченная пара действительных чисел a и b. Два комплексных числа (a;b) и (c;d) называются равными тогда и только тогда, когда a=c и b=d.

лгебраическая форма комплексного числа. Запись a+bi называется алгебраической формой комплексного числа z=(a; b); при этом число a называется действительной частью комплексного числа z, bi - его мнимая часть. Основное свойство числа i состоит в том, что произведение i * i аравно -1, т. е. .

Если мнимая часть комплексного числа аa+bi отлична от нуля, то такое число называется мнимым; если при этом a=0, т. е. число имеет вид bi, то оно называется чисто мнимым; если у комплексного числа a+bi мнимая часть равна нулю, то получается действительное число a.

2. Из истории.

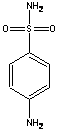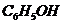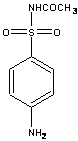Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система равнений , не имеющая решений во множестве действительных чисел, имеет решения вида , лчисто отрицательными и даже софистически отрицательными, считал их бесполезными и старался их не потреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но же в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были становлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название лмнимые числа ввел в 1637 году французский математик и философ Р. Декарт, в 1 году один из крупнейших математиков XV века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа 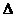а(мнимой единицы). Этот символ вошел во всеобщее потребление благодаря К. Гауссу. Термин комплексные числ так же был введен Гауссом в 1831 году. Слово комплекс (от

латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.

В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.

Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XV веков была построена общая теория корней n-ых степеней сначала из отрицательных, за тем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра (1707): .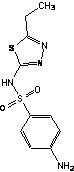

В конце XV века французский математик Ж. Лагранж смог сказать, что математический анализ же не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных равнений с постоянными коэффициентами. Такие равнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов.

Хотя в течение XV века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. По этому французский ченый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, - только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами.

Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы иероглифы нелепых количеств Л. Карно.

3. Заключение

Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения.

Комплексные числа широко применяются не только в математике, но также в физике и технике. Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с величинами, которые изображаются векторами

4. Список используемой литературы:

1) Математика Гусев В.А., Мордкович А.Г. ( Просвещение 1990 г.);

2) Справочник по элементарной математике М.Я. Выгодский (Москва 1966 г.);

3) Энциклопедический словарь юного математика

(ссылка более недоступнаp>