Читайте данную работу прямо на сайте или скачайте
Элементарные конформные отображения
ЕЛЕЦ
ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ.
КУРСОВАЯ РАБОТА
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Тема: Элементарные конфортные отображения
Выполнила: студентка группы М-31
физико-математического факультета
Е.Г. Петренко
Научный руководитель:
О.А. Саввина
1998 г.
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Краткая справка.
Пусть имеются два множества комплексных точек 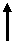


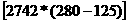 аточку (или точки)
аточку (или точки) 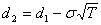
 со значениями в множестве
со значениями в множестве 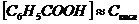



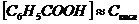
Задание функции  аэквивалентно заданию двух действительных функций
аэквивалентно заданию двух действительных функций  аи тогда
аи тогда  а, где
а, где 
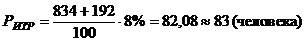
1.  а
а а- линейная функция.
Определена при всех
а- линейная функция.
Определена при всех 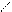
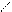
 а. Функция
а. Функция 
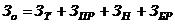

 сжимает)
ее в
сжимает)
ее в  араз и после этого осуществляет параллельный сдвиг на величину
араз и после этого осуществляет параллельный сдвиг на величину 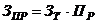
2. 
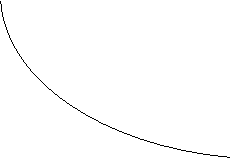



3.  а- показательная функция. По определению
а- показательная функция. По определению 

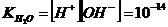

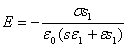 ;
; 

Определена на всей комплексной плоскости и непрерывна на ней. 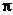

 а
а

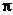
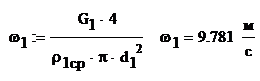 а,
а, 
4. 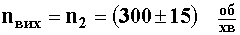 натуральный логарифм). По определению:
натуральный логарифм). По определению: 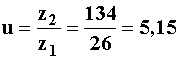

 называется главным значением
называется главным значением 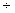
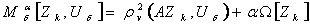
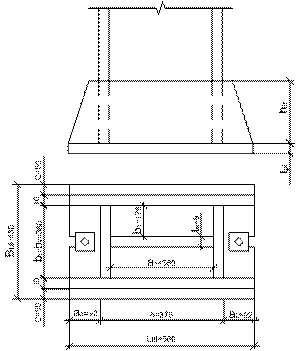
 а- бесконечно-значная функция, обратная к
а- бесконечно-значная функция, обратная к 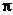
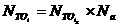
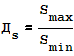
5. 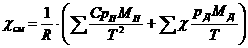 а
а

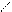
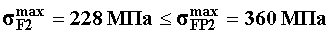
6. Тригонометрические функции 

 а По определению,
а По определению, 

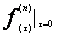 а;
а; 
7. Гиперболические функции. Определяются по аналогии с такими же функциями действительной переменной, именно:
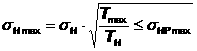 а,
а, 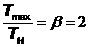
Определены и непрерывны на всей комплексной плоскости.
Задачи с решением.
1)
Найти модули и главные значения аргументов комплексных чисел:  а
а 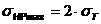
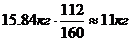
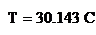
Решение. По определению,


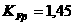
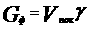

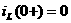
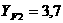 а
а 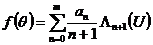 а
а 
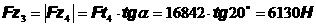
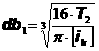

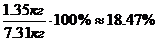


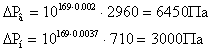

Найти суммы:
1) 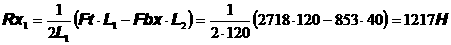
2) 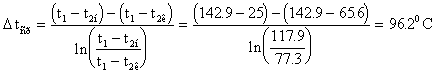
Решение. Пусть: 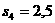
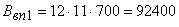
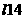
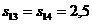
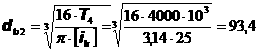 ;
Преобразуя, получим:
;
Преобразуя, получим:
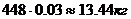
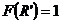
3. Доказать, что:
1) 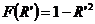 2)
2)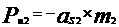
3)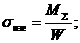 4)
4)
Доказательство:
1) По определению, 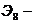
2) 
3) 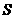 а;
а; 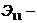
Выразить через тригонометрические и гиперболические функции действительного аргумента действительные и мнимые части, также модули следующих функций: 1) 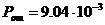
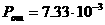

Решение:  аи, учитывая результаты предыдущего примера, получим:
аи, учитывая результаты предыдущего примера, получим:
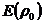
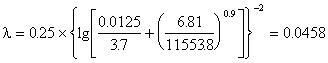
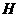
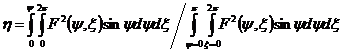
Напомним,
что 
2) 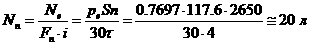
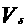 а
а 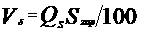
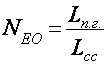
3) 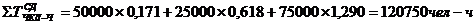
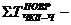 а,
а, 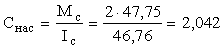 ,
,
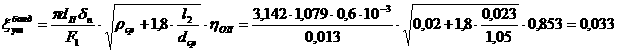 а,
а, 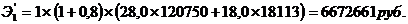 а.
а.
Найти действительные и мнимые части следующих значений функций: 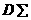 ;
; 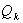 ;
; 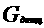
Решение. Следуя решению примера 4, будем иметь:
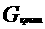 а;а
а;а  а;а
а;а 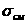 а;
а; 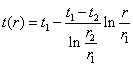
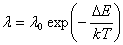 а;
а; 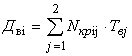
Вычислить:
1) 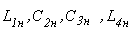 3)
3) 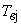 ; 5)
; 5) 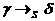
2) 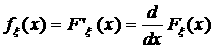 4)
4) 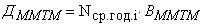 а; 6)
а; 6) 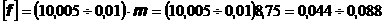 а;
а;
Решение. По определению, 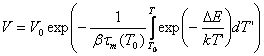

1)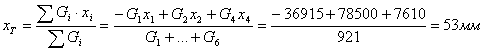
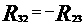
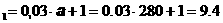
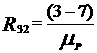
2) 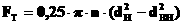
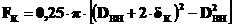
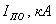
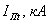
3) 
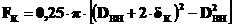
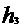
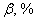
4)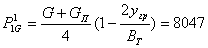
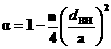
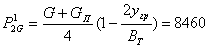
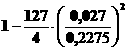
5)
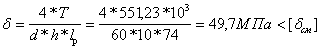 а
а 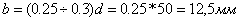
6)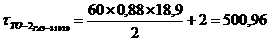
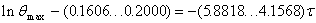
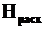

Найти все значения следующих степеней:
1) 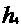 2)
2) 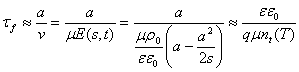 а; 3)
а; 3)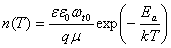 а; 4)
а; 4)
Решение. Выражение  адля любых комплексных
адля любых комплексных 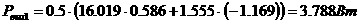 аи
аи 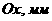

1) 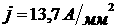
2)
3)а 
4) 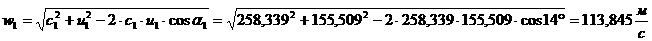
8. Доказать следующие равенства:
1) 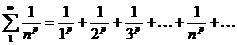
2)а 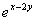
3) 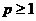
Доказательство: 1) 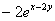
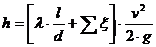
 а, откуд
а, откуд 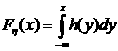
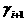
Решив это равнение, получим 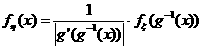
 аи
аи 
2) 
 а
а 
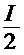
3) 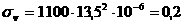
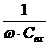
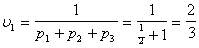
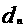
Отсюд