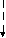Н. Э. Баумана Пузанов В. П. Лекции
| Вид материала | Лекции |
- Пузанов Александр Сергеевич. Он рассказывал о том, что наша планета постепенно переходит, 54.47kb.
- Н. Э. Баумана (мгту им. Н. Э. Баумана) Военное обучение в мгту им. Н. Э. Баумана, 3073.69kb.
- Московском Государственном Техническом университете им. Н. Э. Баумана. Адрес: 105005,, 240.52kb.
- Н. Э. Баумана Федоров И. Б. 2000 г. Положение об организации учебного процесса в мгту, 225.02kb.
- Н. Э. Баумана "утверждаю" Первый проректор проректор по учебной работе мгту им., 114.55kb.
- Доклад на заседании Ученого совета мгту им. Н. Э. Баумана 28. 06., 228.72kb.
- Москва, 9-11 сентября 2009 г. Московский государственный технический университет им., 94.15kb.
- Программа регламент проведения школы-семинара Москва Издательство мгту им. Н. Э. Баумана, 191.55kb.
- Критерии оценки качества лекции, 33.79kb.
- План расположения главного учебного корпуса мгту им. Н. Э. Баумана: План главного учебного, 41.59kb.
Московский государственный технический университет
им. Н. Э. Баумана
Пузанов В. П.
ЛЕКЦИИ
ПО КУРСУ «ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»
ТЕОРИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ И РЕГУЛИРОВАНИЯ.
Факультет «Специальное машиностроение»
Кафедра «Подводные роботы и аппараты»
2003 год.
Частотные методы определения параметров периодических решений.
Пусть структурная схема гармонически линеаризованной системы имеет вид:
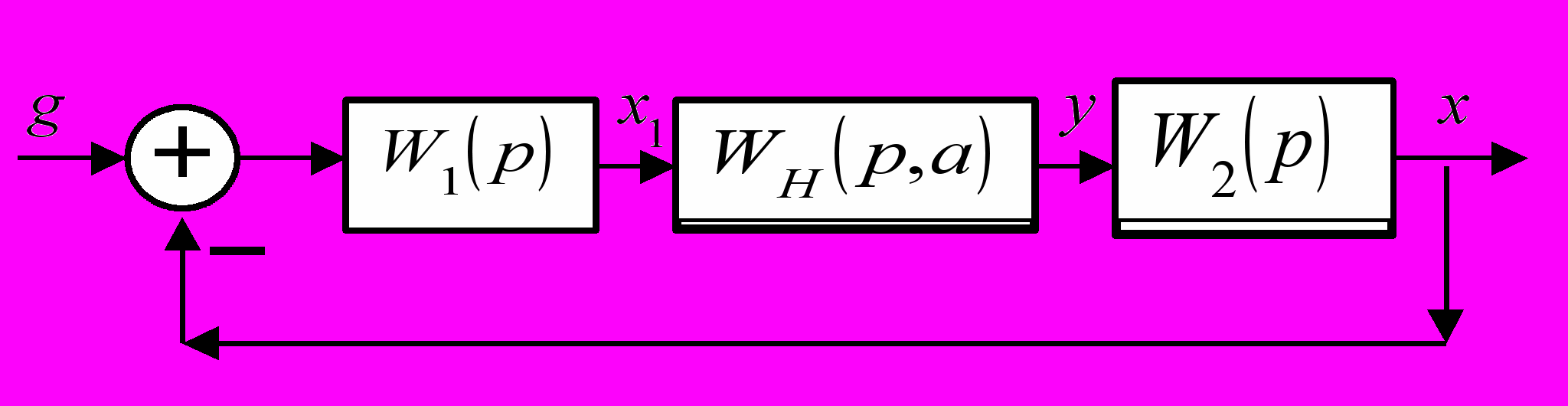
Составим уравнения гармонически линеаризованной системы управления при
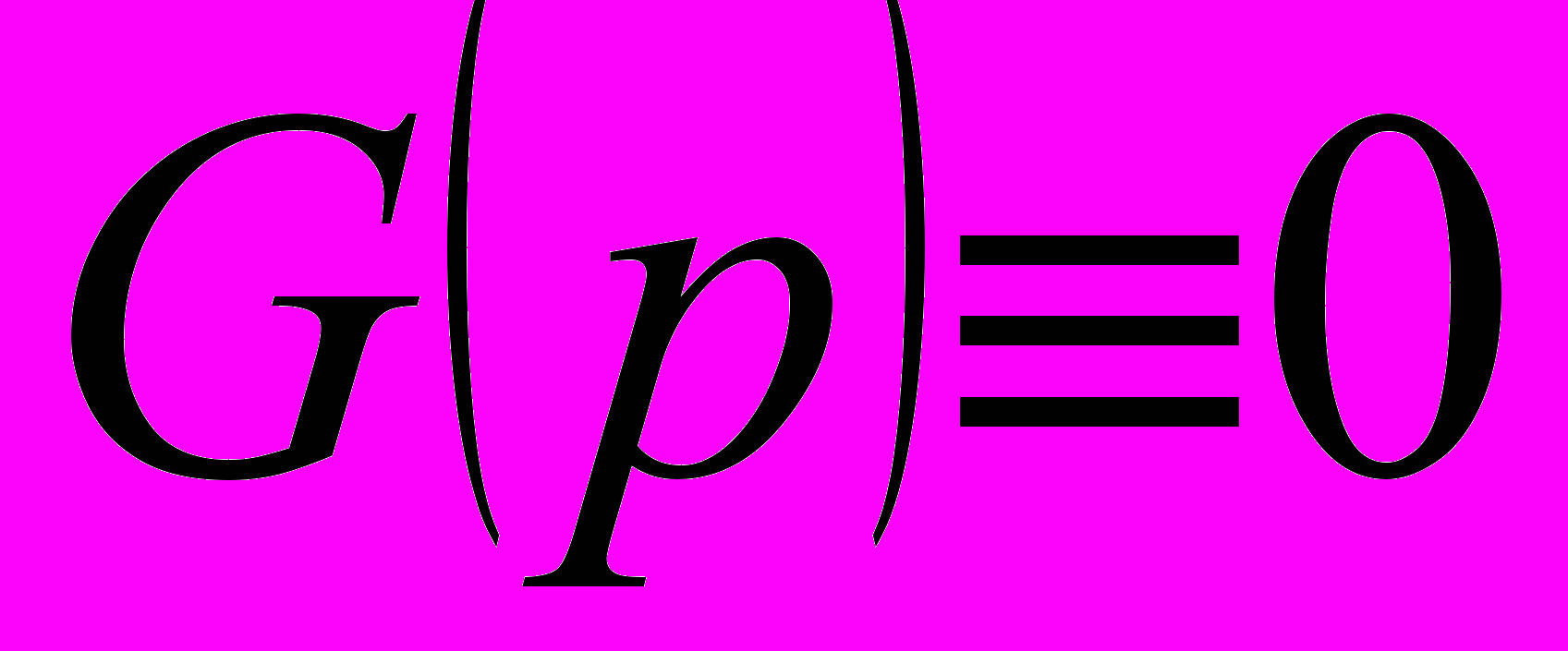 .
.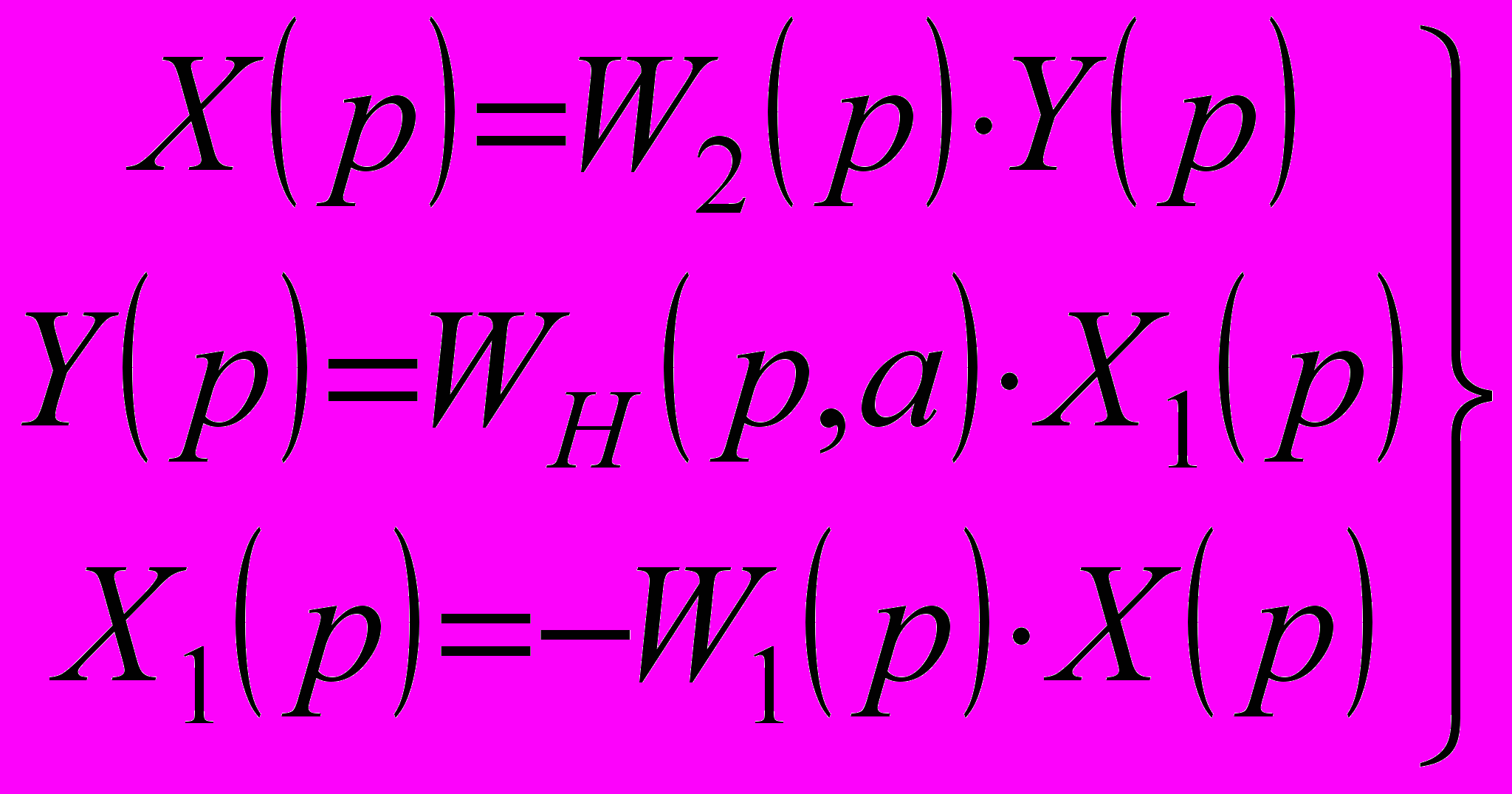 . (1)
. (1)Из системы уравнений (1) получаем
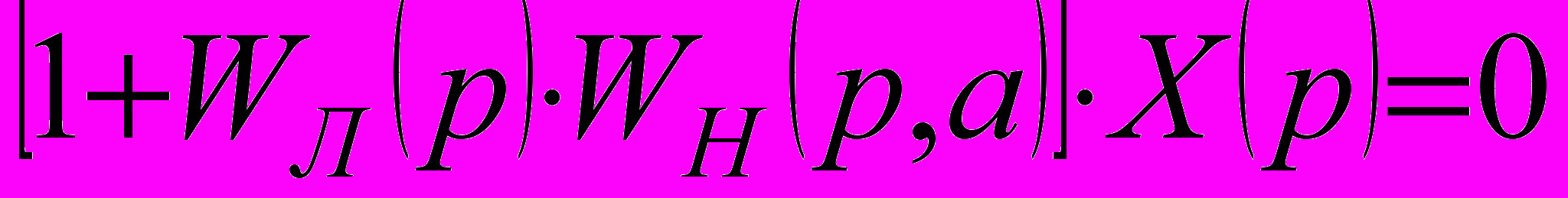 , (2)
, (2)где
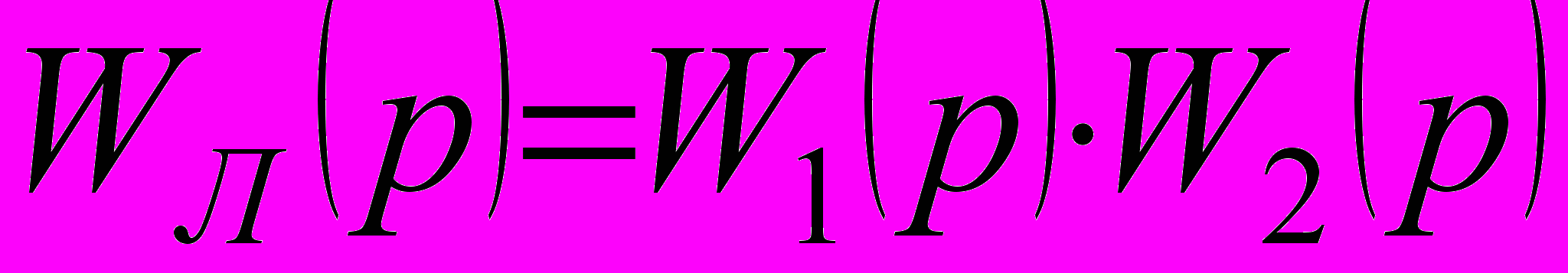 – передаточная функция линейной части системы
– передаточная функция линейной части системы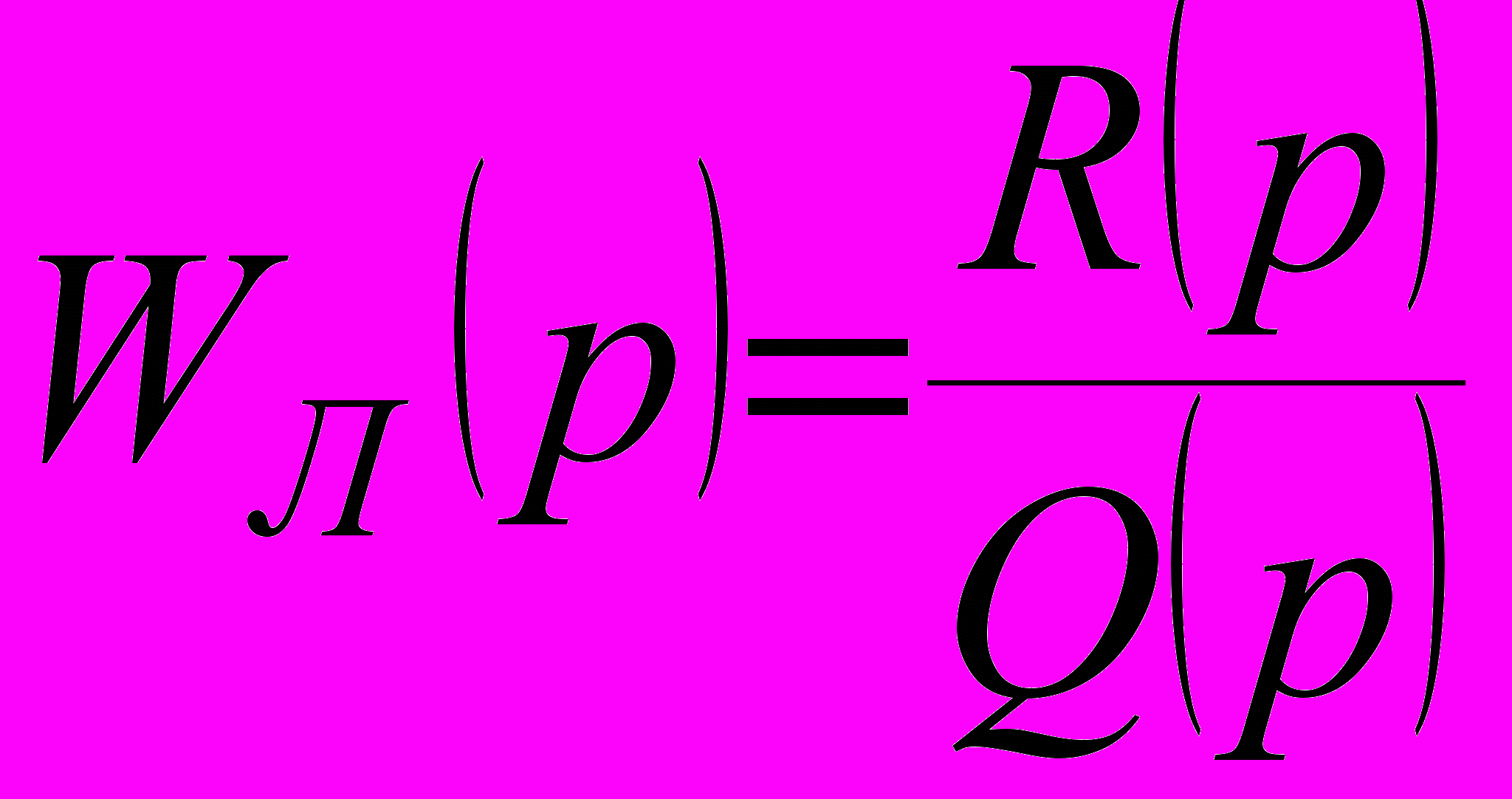 , (3)
, (3)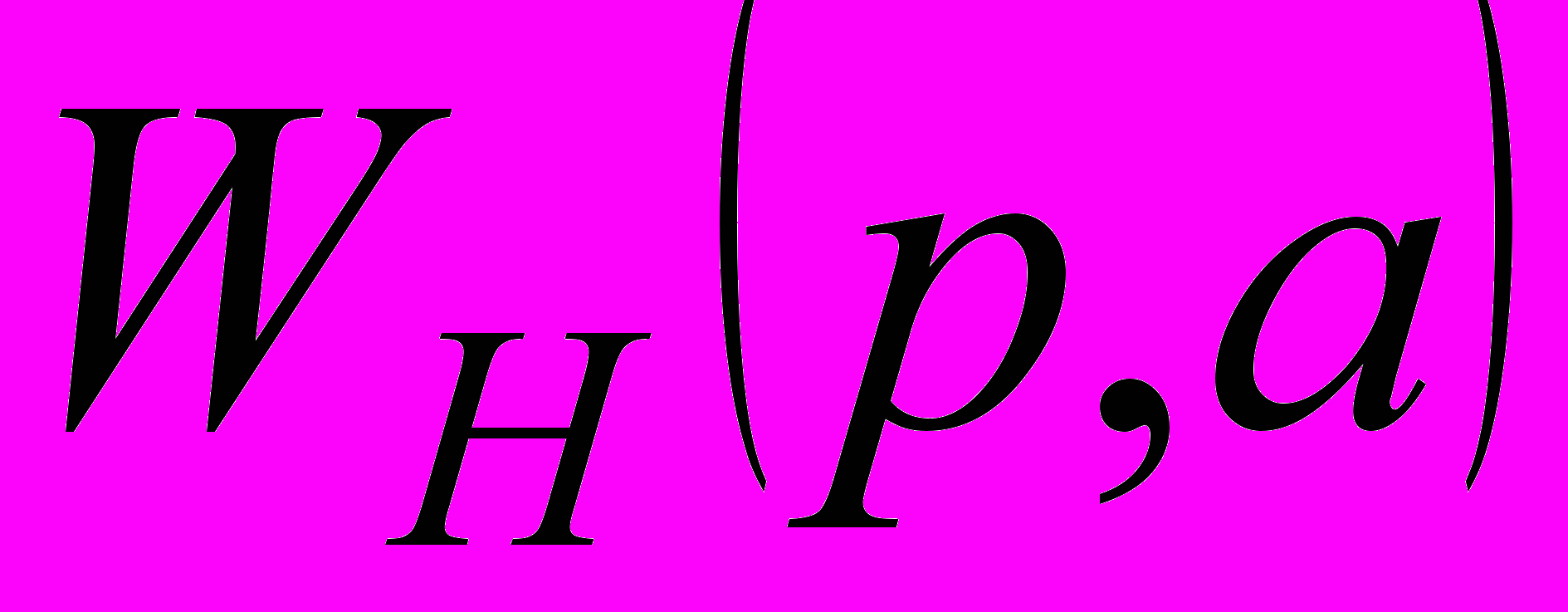 – передаточная функция гармонически линеаризованного нелинейного звена
– передаточная функция гармонически линеаризованного нелинейного звена . (4)
. (4)Обозначим через
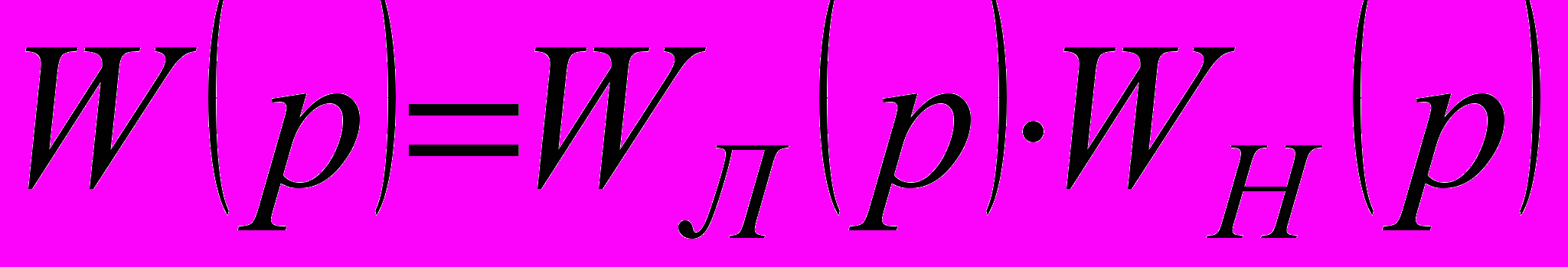 (5)
(5)передаточную функцию разомкнутой цепи гармонически линеаризованной системы. Амплитудно-фазовая частотная характеристика разомкнутой цепи гармонически линеаризованной системы
 . (6)
. (6)Периодическое решение гармонически линеаризованной системы получается при наличии в характеристическом уравнении замкнутой системы пары чисто мнимых корней. Система находится на границе устойчивости. По критерию Найквиста это соответствует прохождению амплитудно-фазовой частотной характеристики разомкнутой цепи гармонически линеаризованной системы
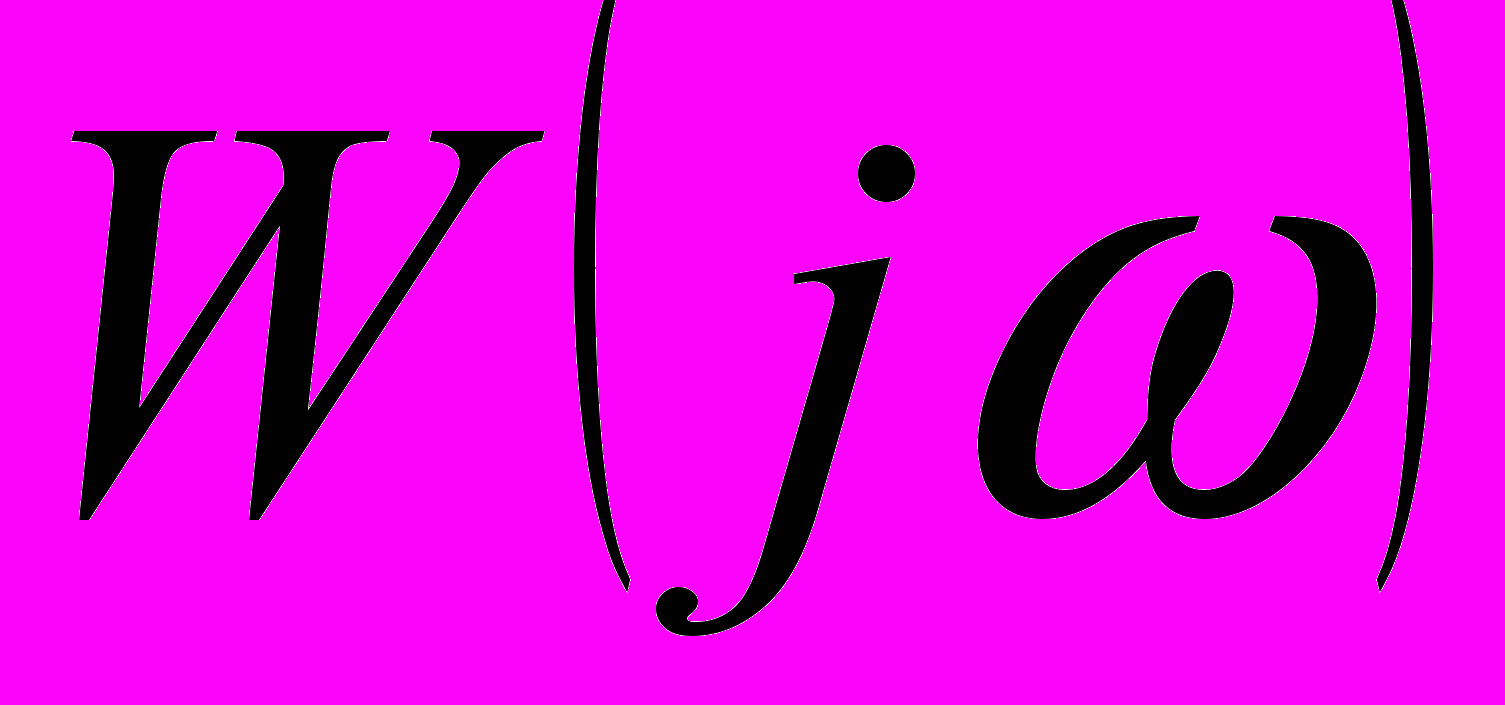 через точку с координатами
через точку с координатами 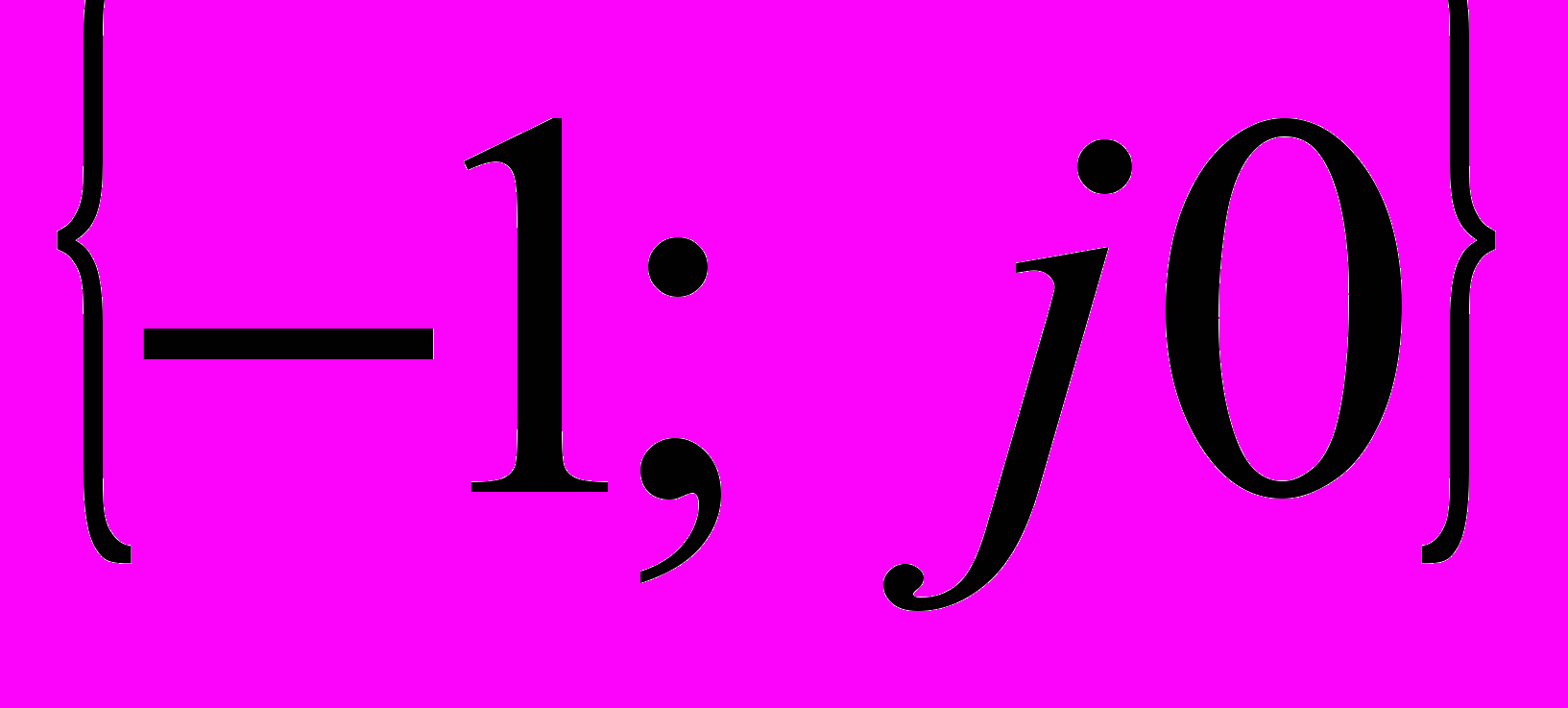 . Следовательно, периодическое решение определяется равенством
. Следовательно, периодическое решение определяется равенством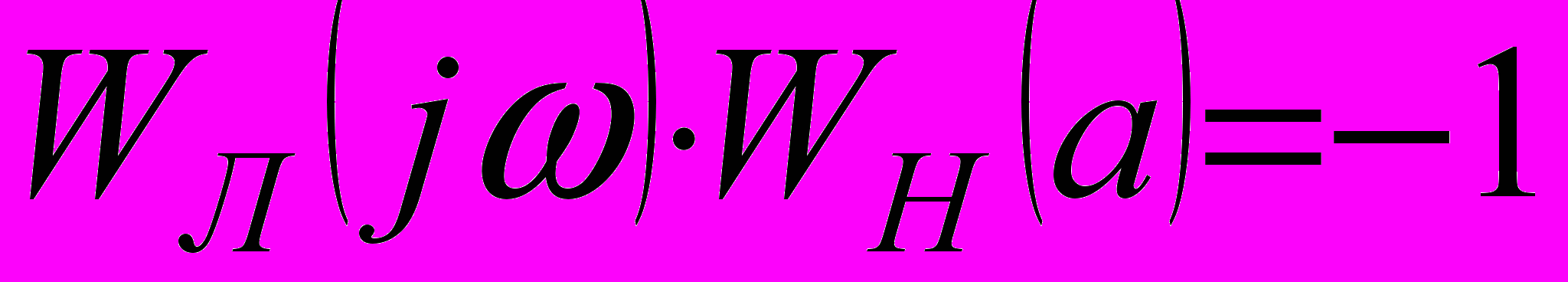 , (7)
, (7)
Из равенства (7) получаем
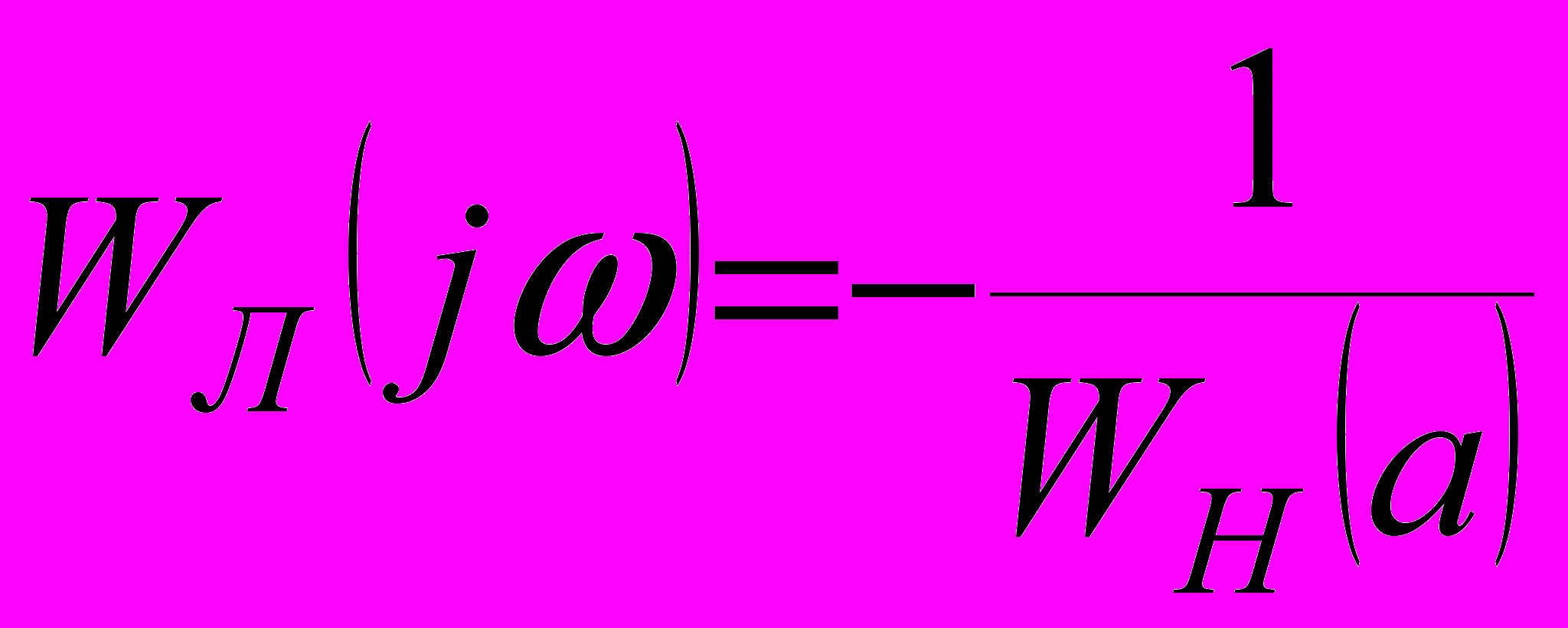 . (8)
. (8)Уравнение (8) определяет искомые значения амплитуды
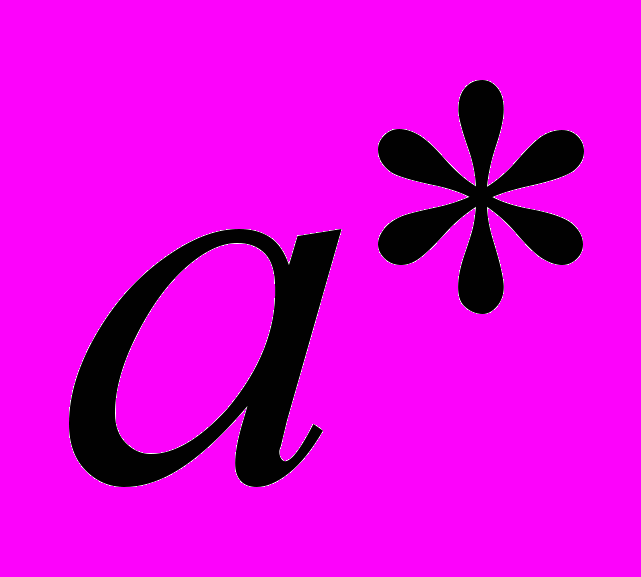 и частоты
и частоты  периодического решения. Уравнение (8) можно решить графическим способом следующим образом.
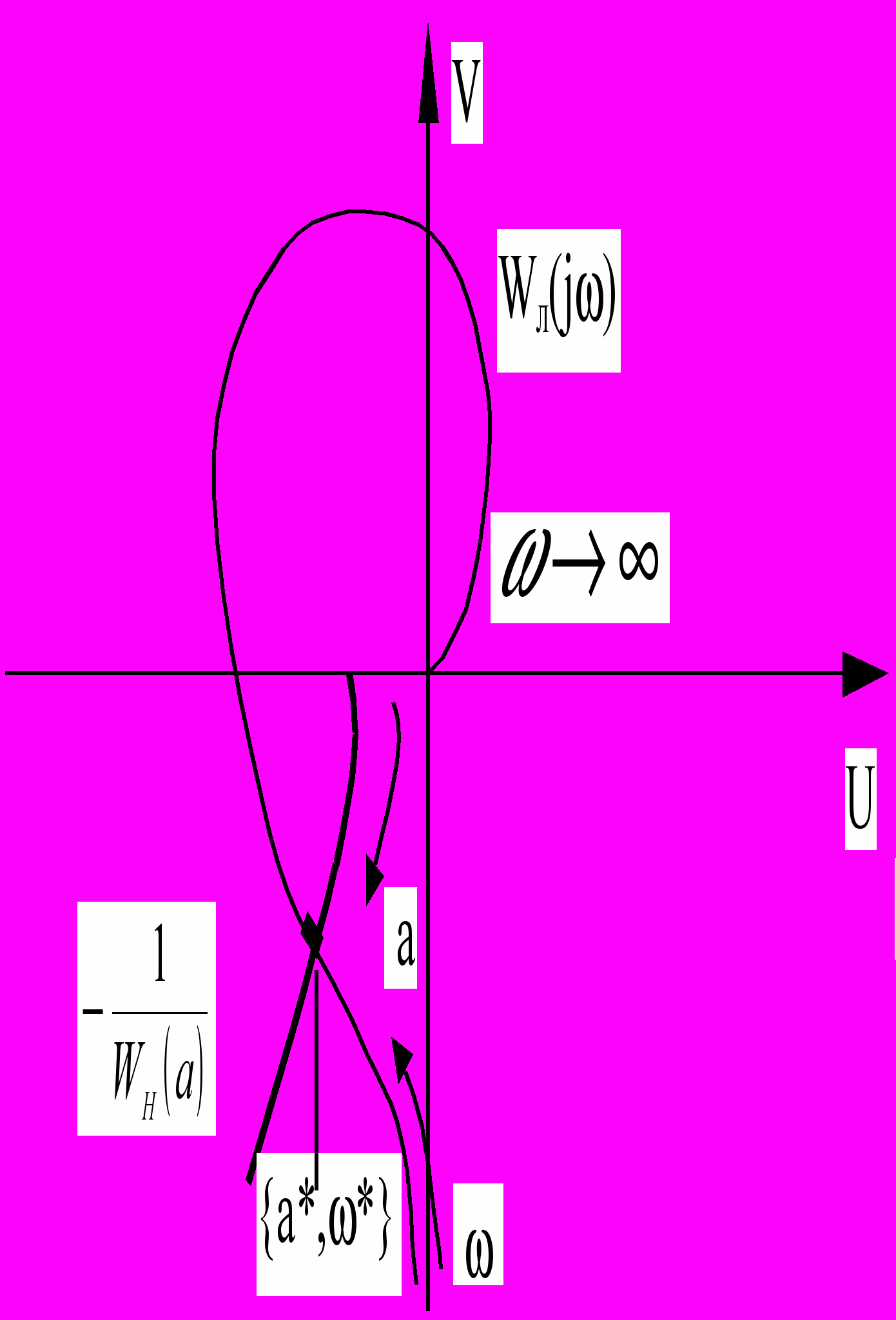
периодического решения. Уравнение (8) можно решить графическим способом следующим образом.- На комплексной плоскости
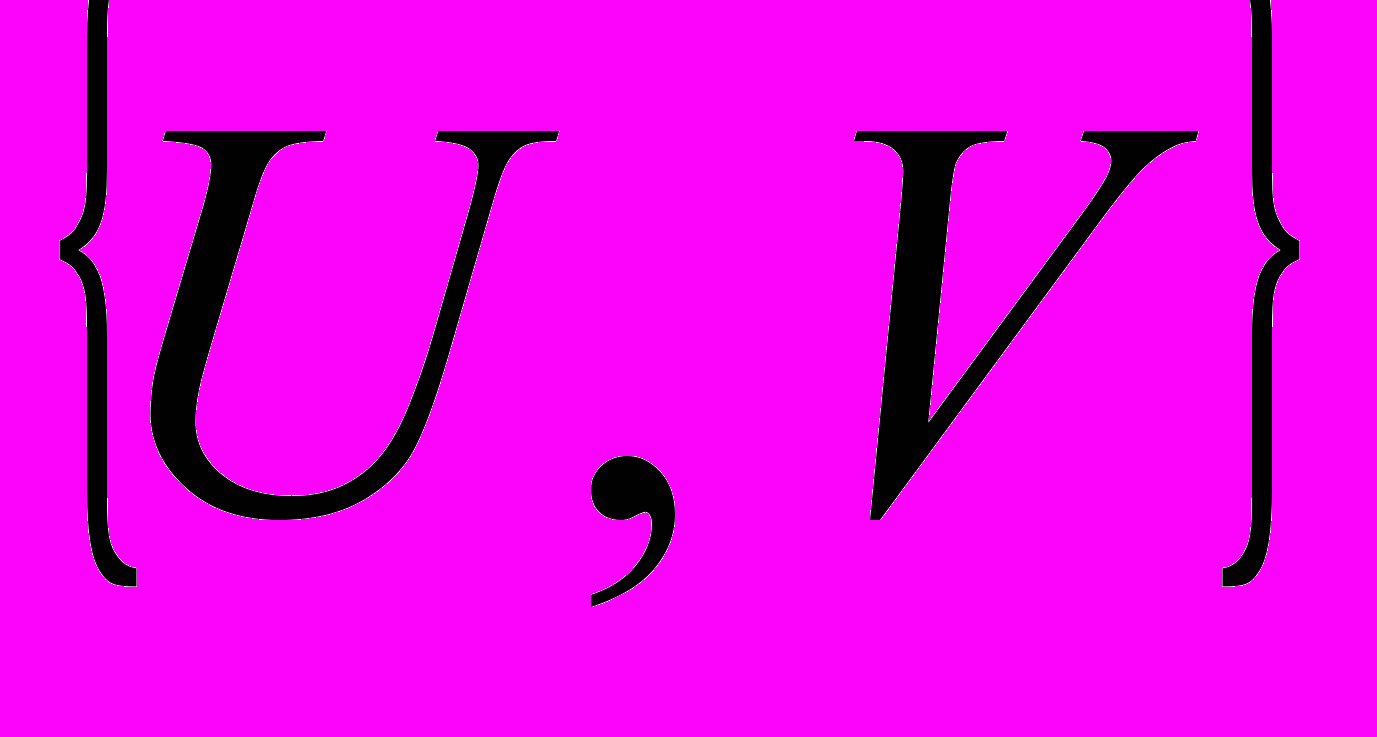 строится амплитудно-фазовая частотная характеристика линейной части
строится амплитудно-фазовая частотная характеристика линейной части 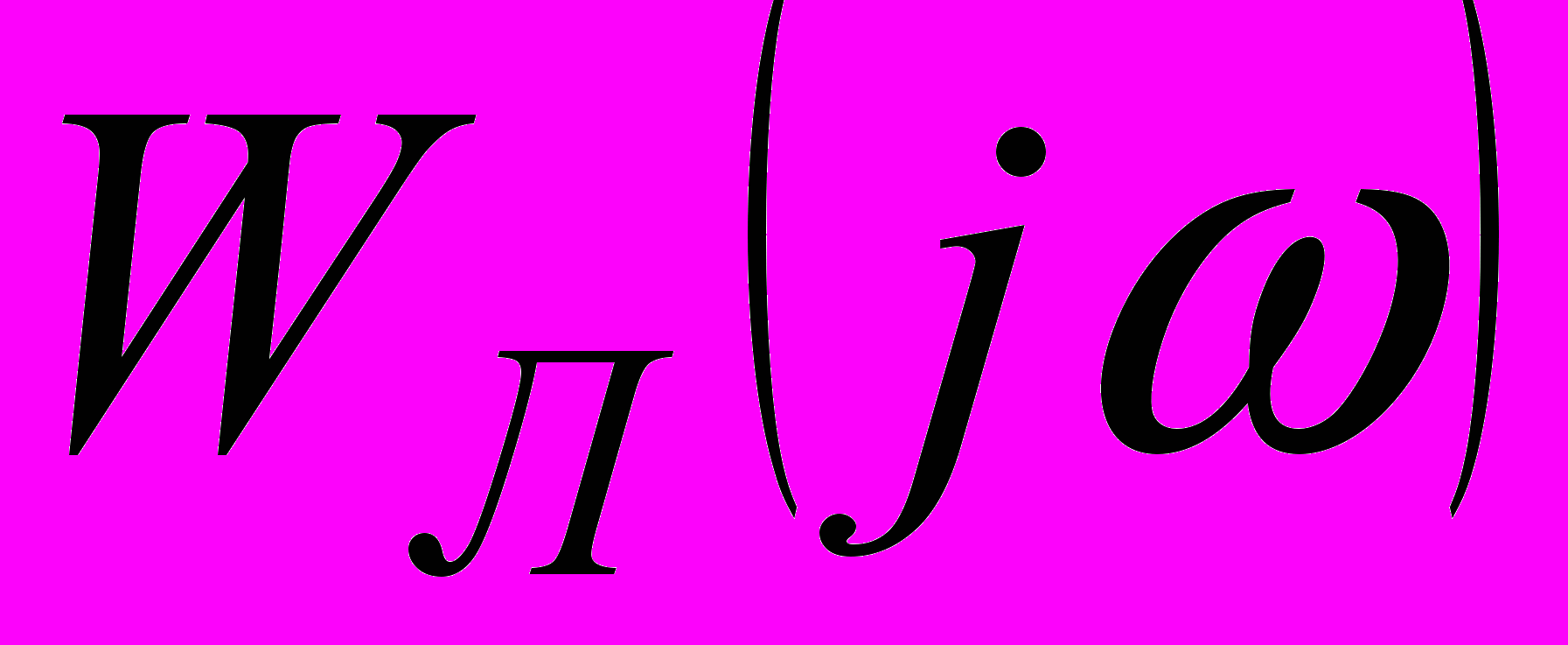 .
.
- На комплексной плоскости
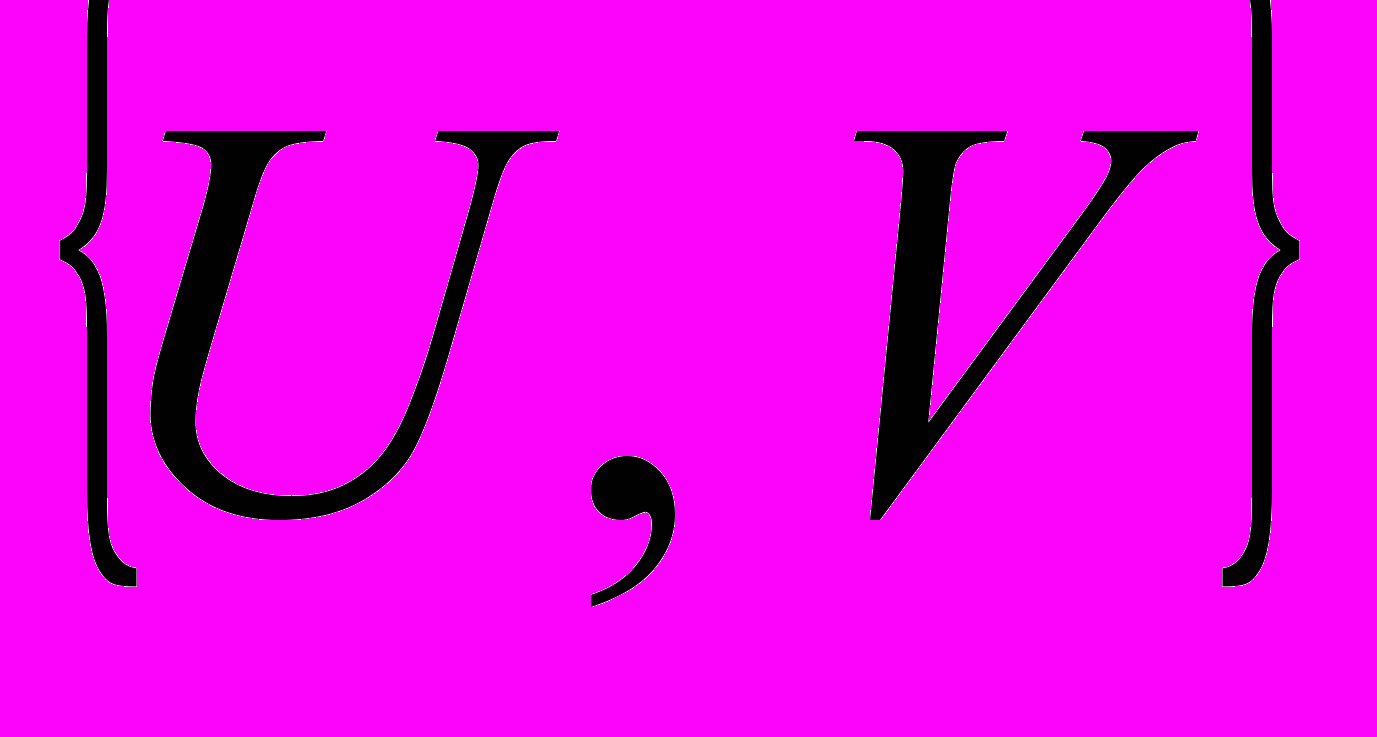 строится амплитудно-фазовая характеристика гармонически линеаризованного звена с передаточной функцией
строится амплитудно-фазовая характеристика гармонически линеаризованного звена с передаточной функцией  .
.
- Точка пересечения построенных графиков определяет величины
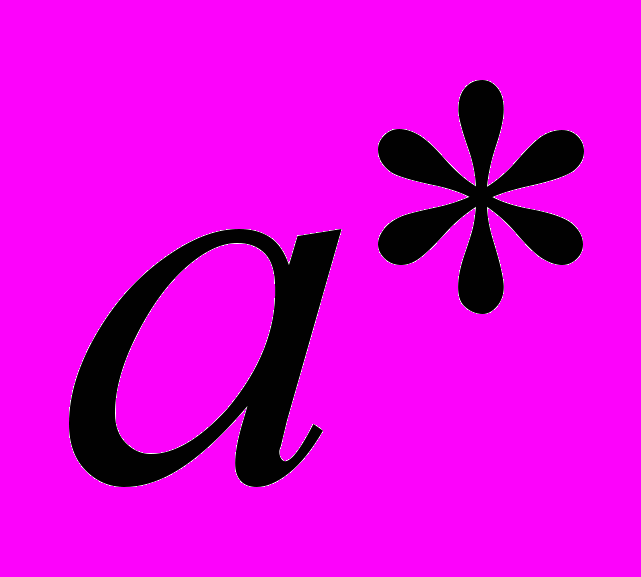 и
и  . При этом значение
. При этом значение  отсчитывается по кривой
отсчитывается по кривой  , а значение
, а значение  – по кривой
– по кривой 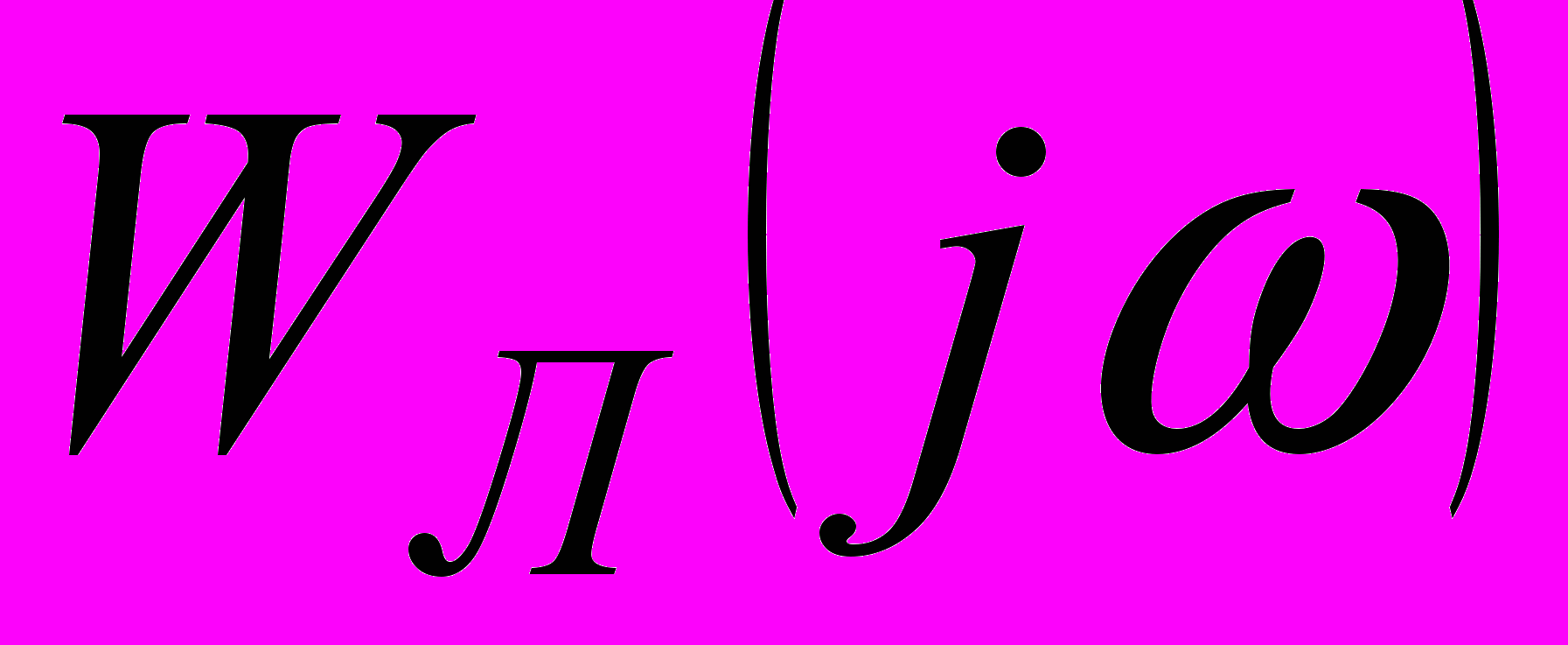 .
.
Вместо уравнения (8) можно воспользоваться двумя скалярными уравнениями
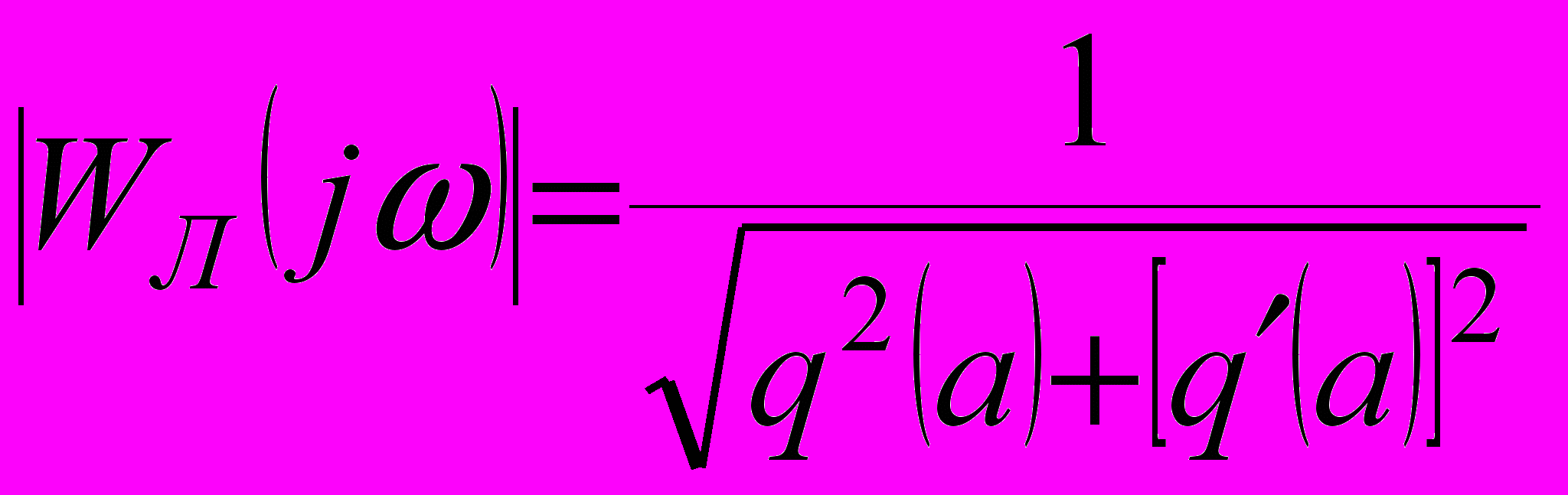 , (9)
, (9)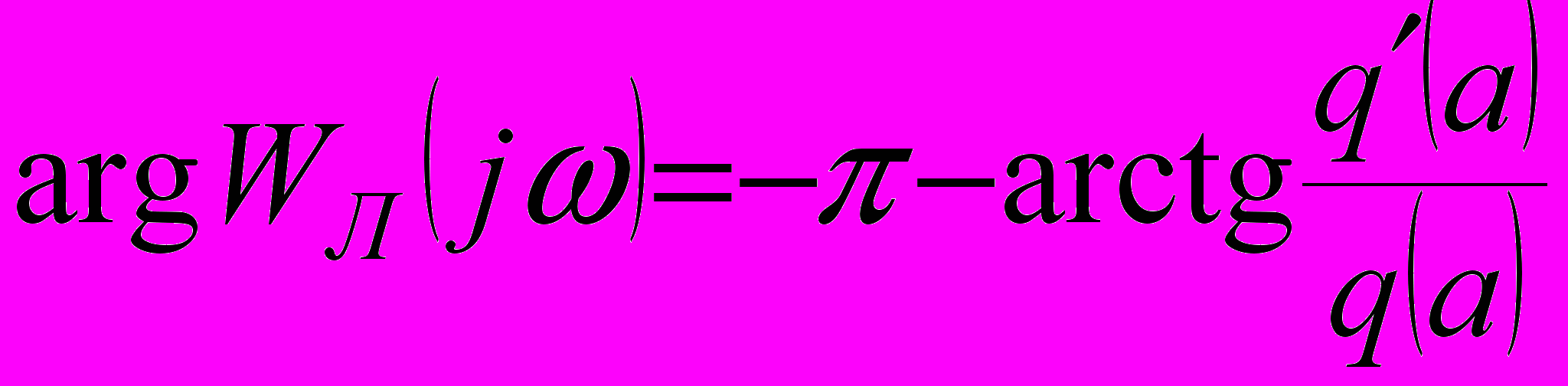 , (10)
, (10)Совместное решение системы уравнений (9) и (10) определяют численные значения искомых параметров периодических решений
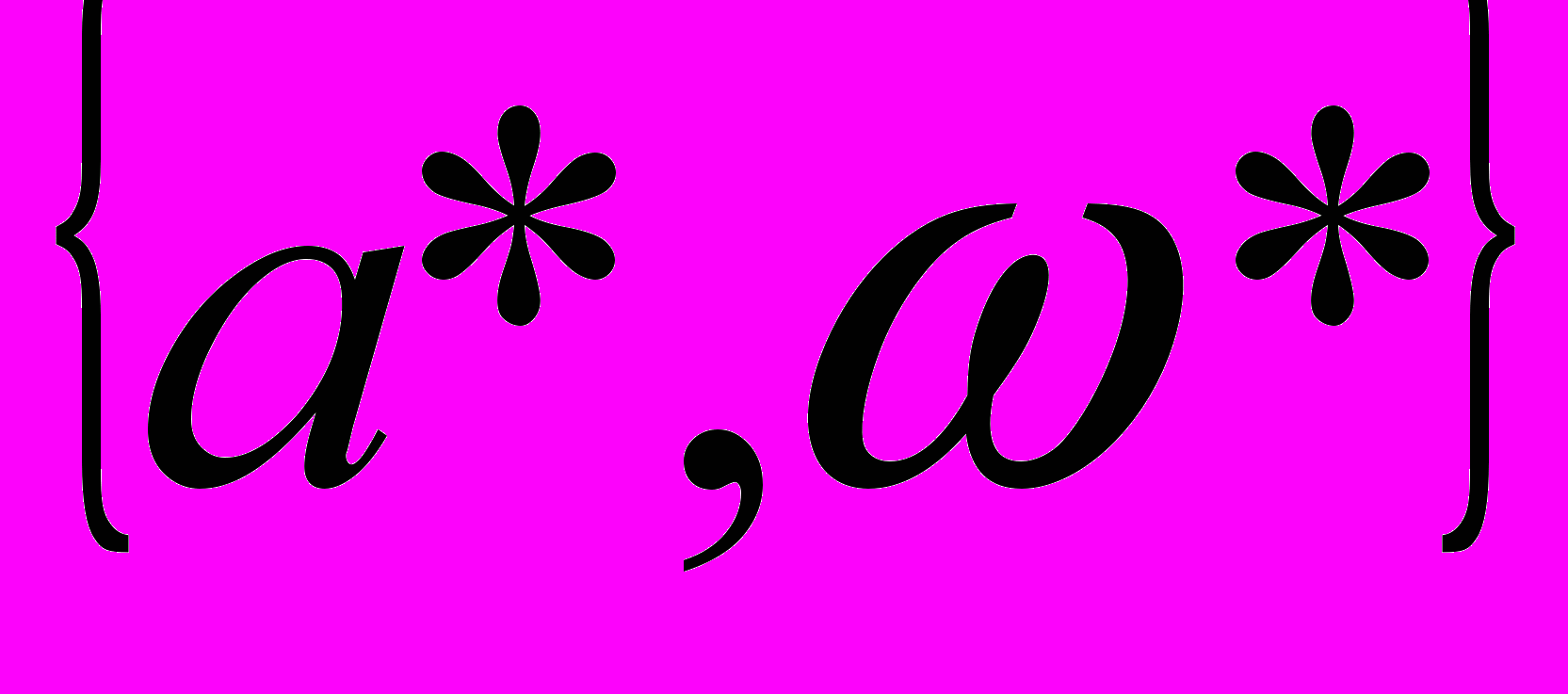 . Последними двумя уравнениями для определения периодического решения графическим способом целесообразно использовать построение в логарифмическом масштабе, привлекая логарифмически частотные характеристики линейной части. Тогда вместо (9) и (10) будем иметь следующие два уравнения
. Последними двумя уравнениями для определения периодического решения графическим способом целесообразно использовать построение в логарифмическом масштабе, привлекая логарифмически частотные характеристики линейной части. Тогда вместо (9) и (10) будем иметь следующие два уравнения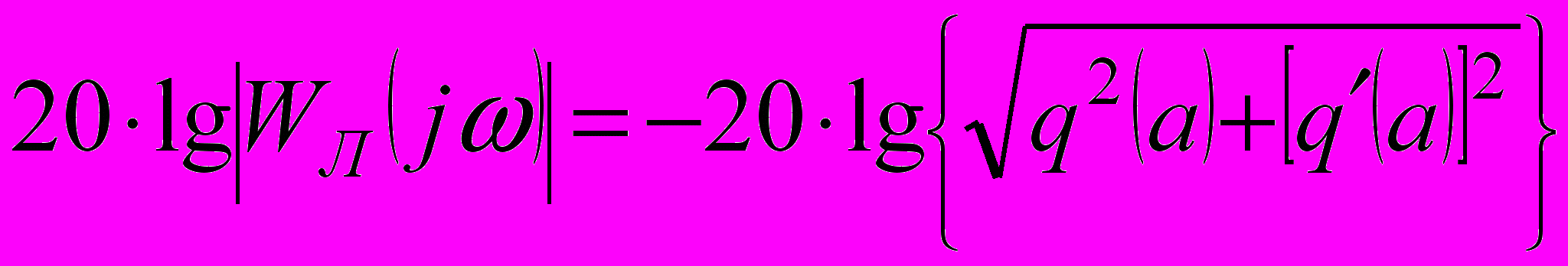 , (11)
, (11) , (12)
, (12)Замечание. Уравнение
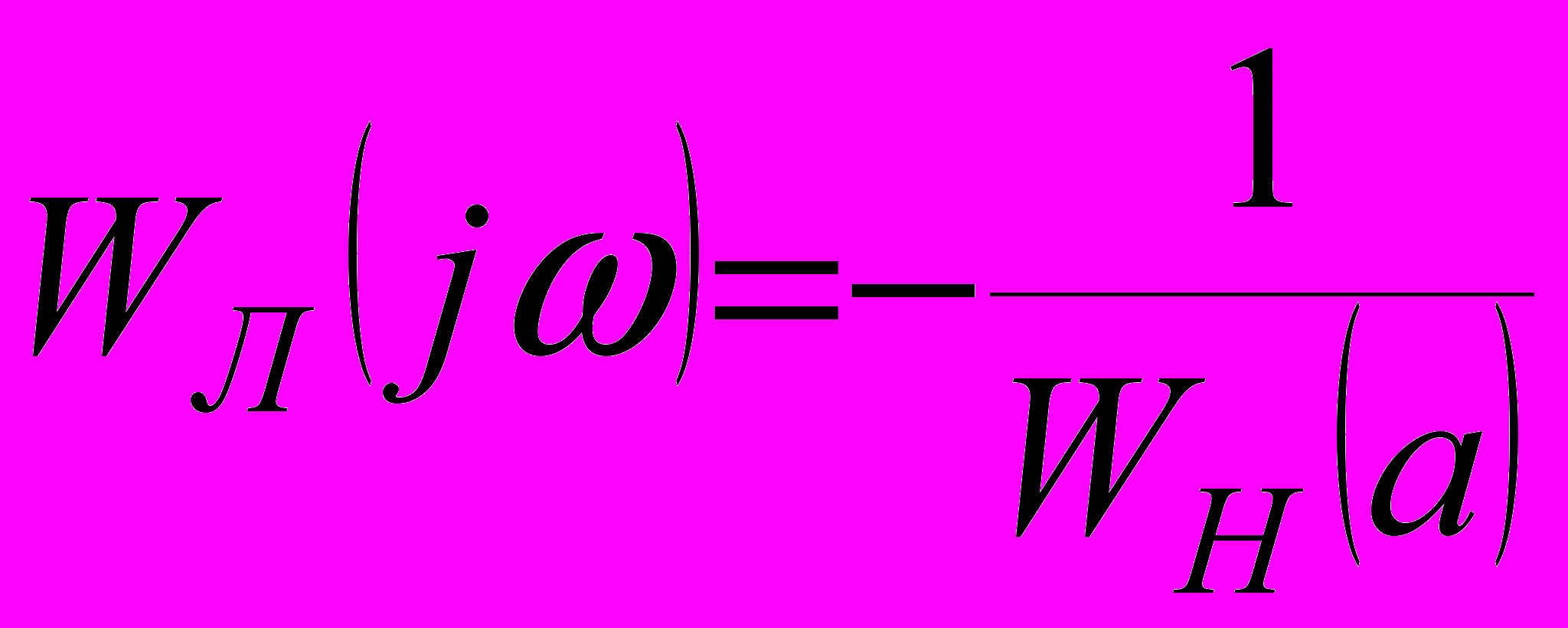 –это равенство двух комплексных чисел. Два комплексных числа равны, если равны их модули и аргументы.
–это равенство двух комплексных чисел. Два комплексных числа равны, если равны их модули и аргументы.Это значит, что уравнение (8) и система уравнений (9), (10) эквивалентны, т.е. равенство (8) эквивалентно двум действительным равенствам (9) и (10) или, что тоже самое равенствам (11) и (12).
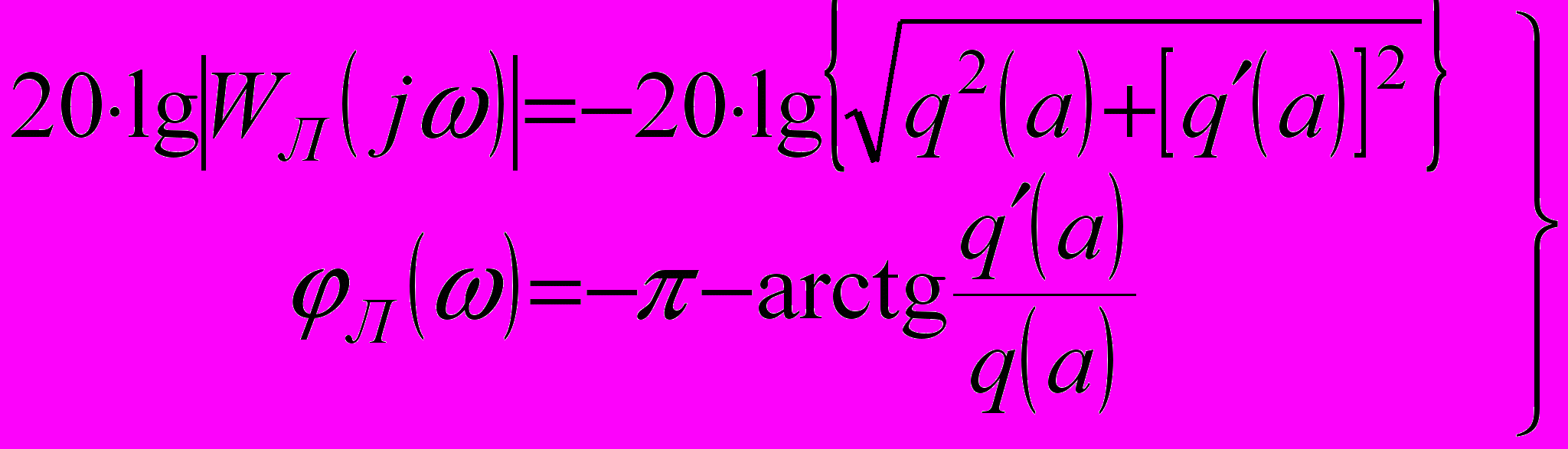 .
.Последовательность действий при графическом способе решения системы уравнений (11), (12)
1. Строится логарифмическая амплитудно частотная характеристика линейной части исследуемой системы
 .
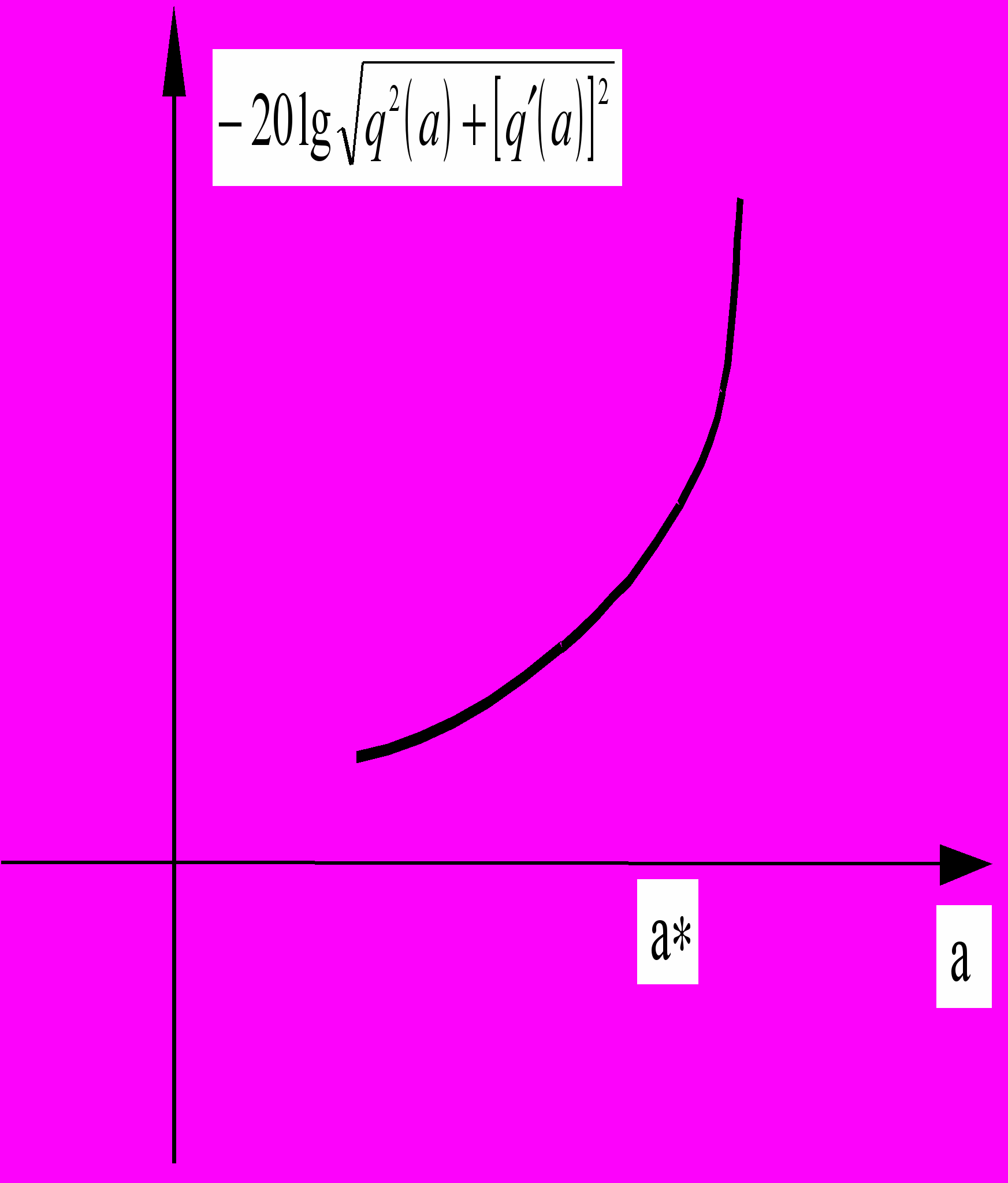
.2. Строится фазочастотная характеристика линейной части исследуемой системы
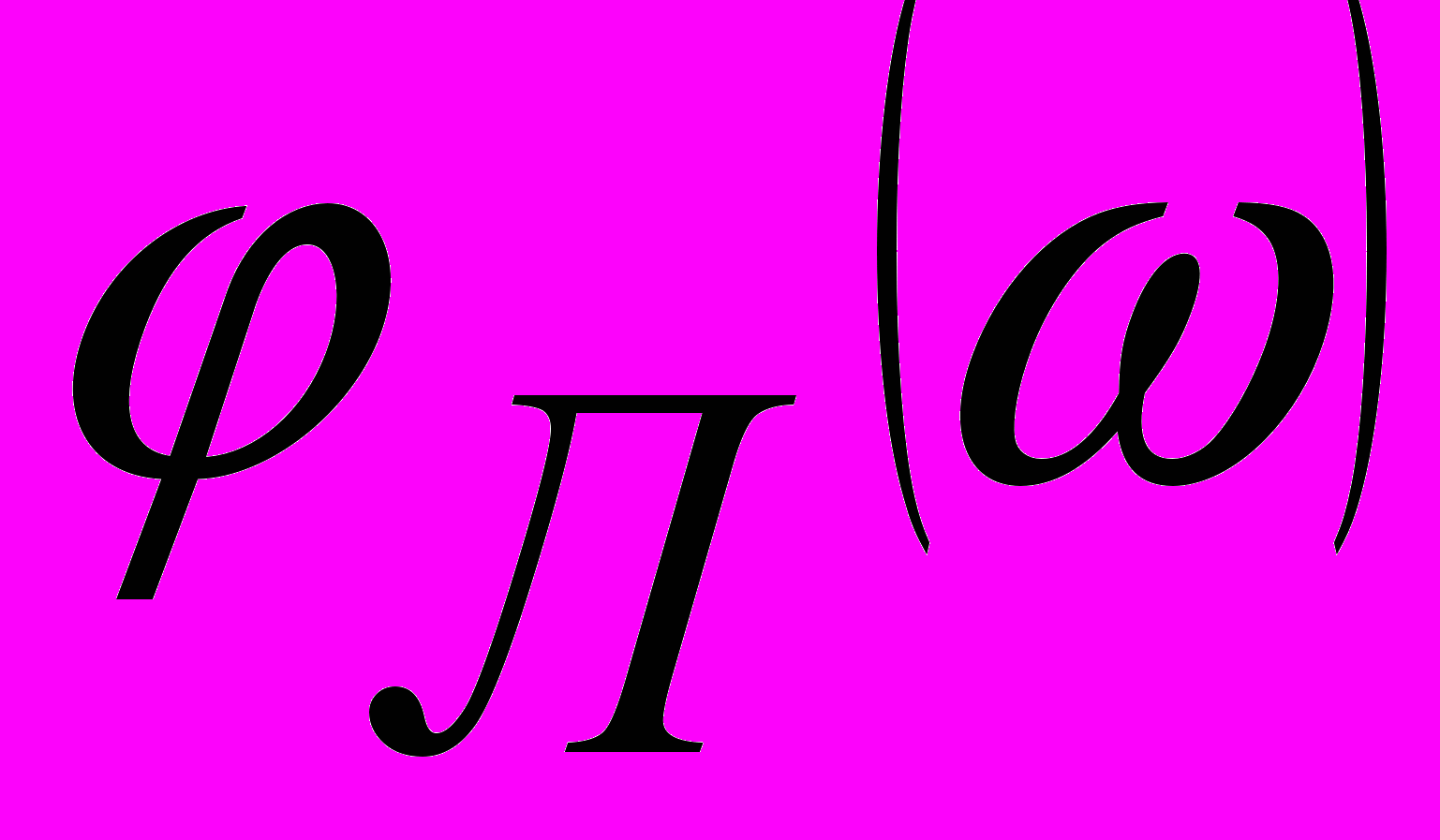 .
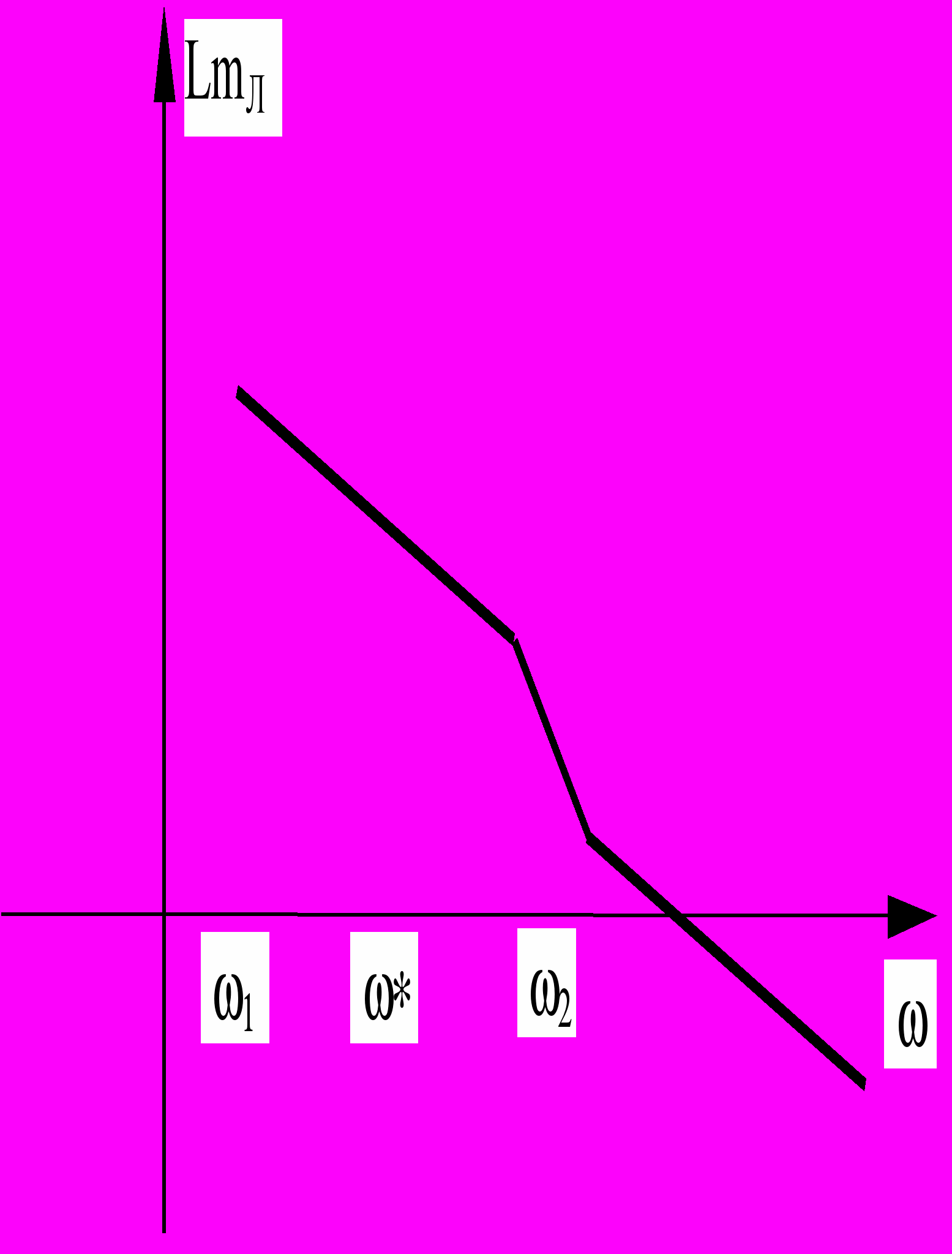
.3.Строится график функции
 , амплитуда
, амплитуда  – берется в натуральном масштабе.
– берется в натуральном масштабе.- Строится график функции
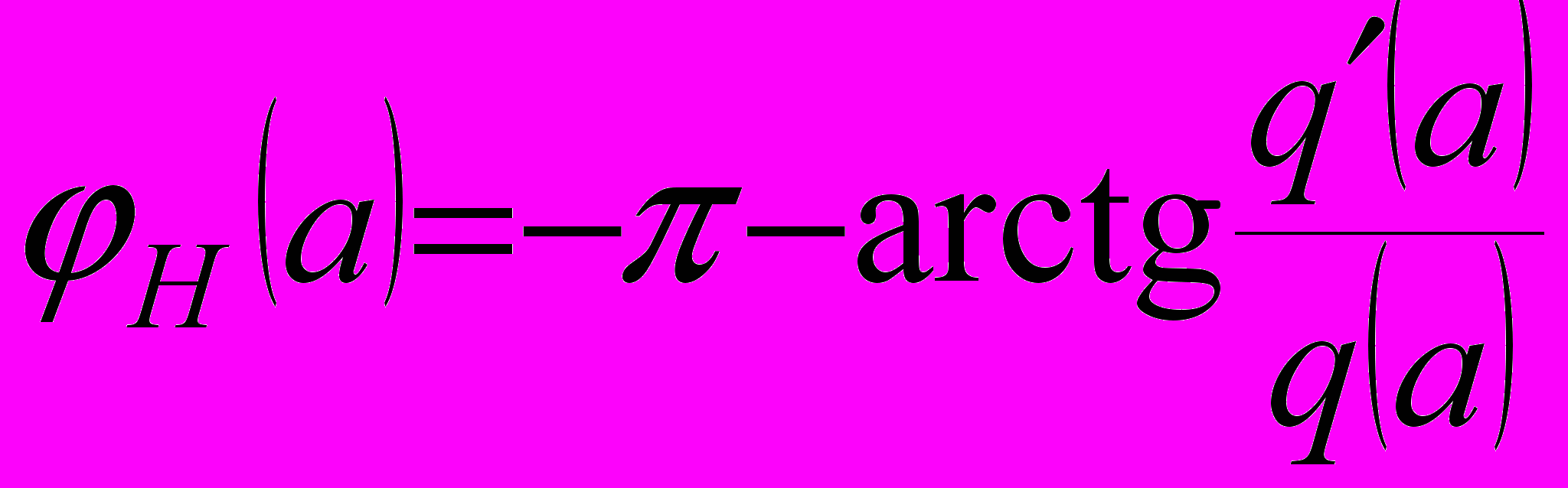 .
.
- Построение кривой
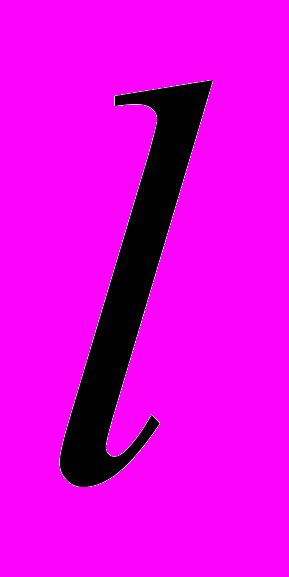 .
.





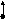










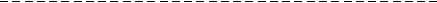








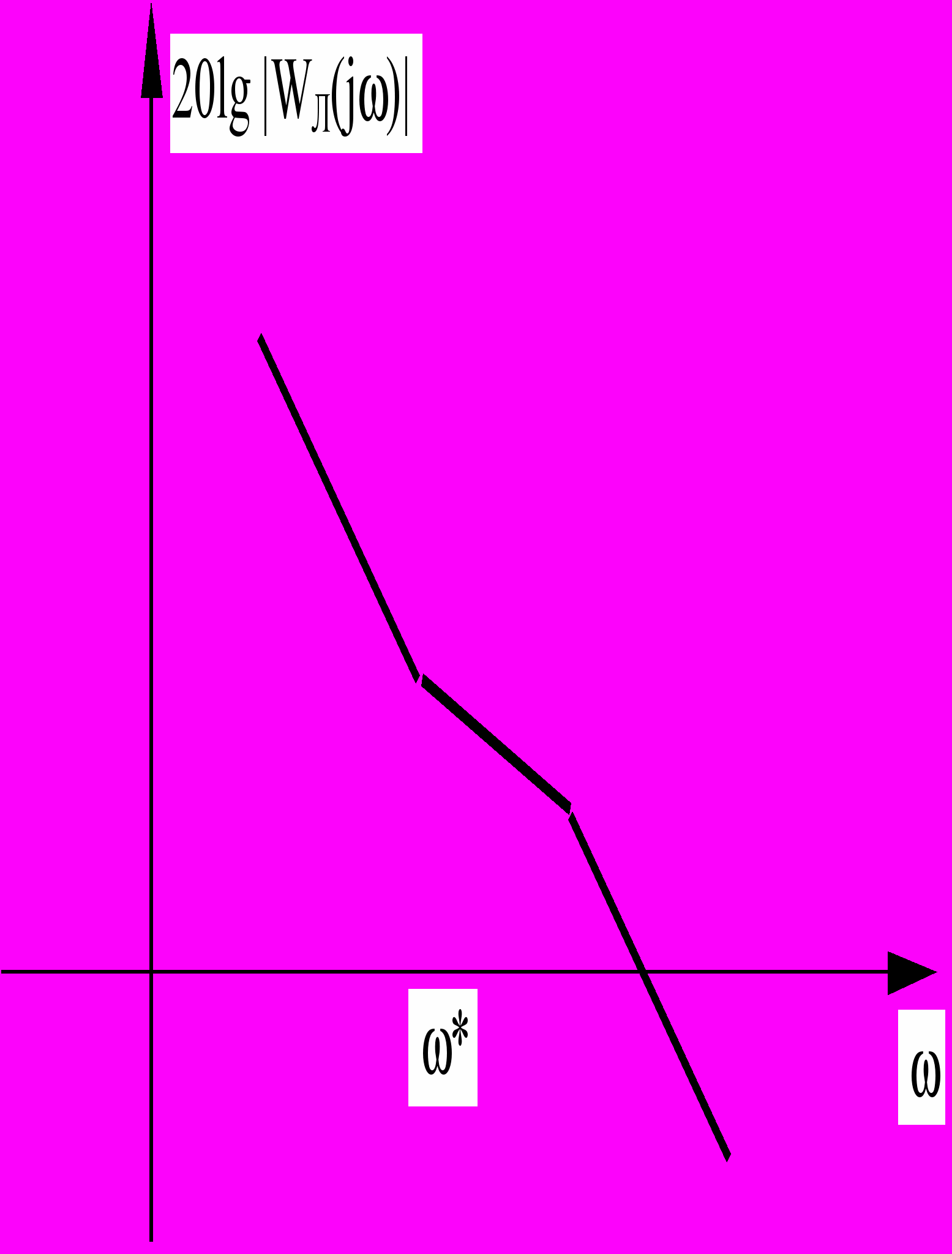
Нахождение периодического решения в случае однозначной нечетной нелинейности упрощается. В этом случае
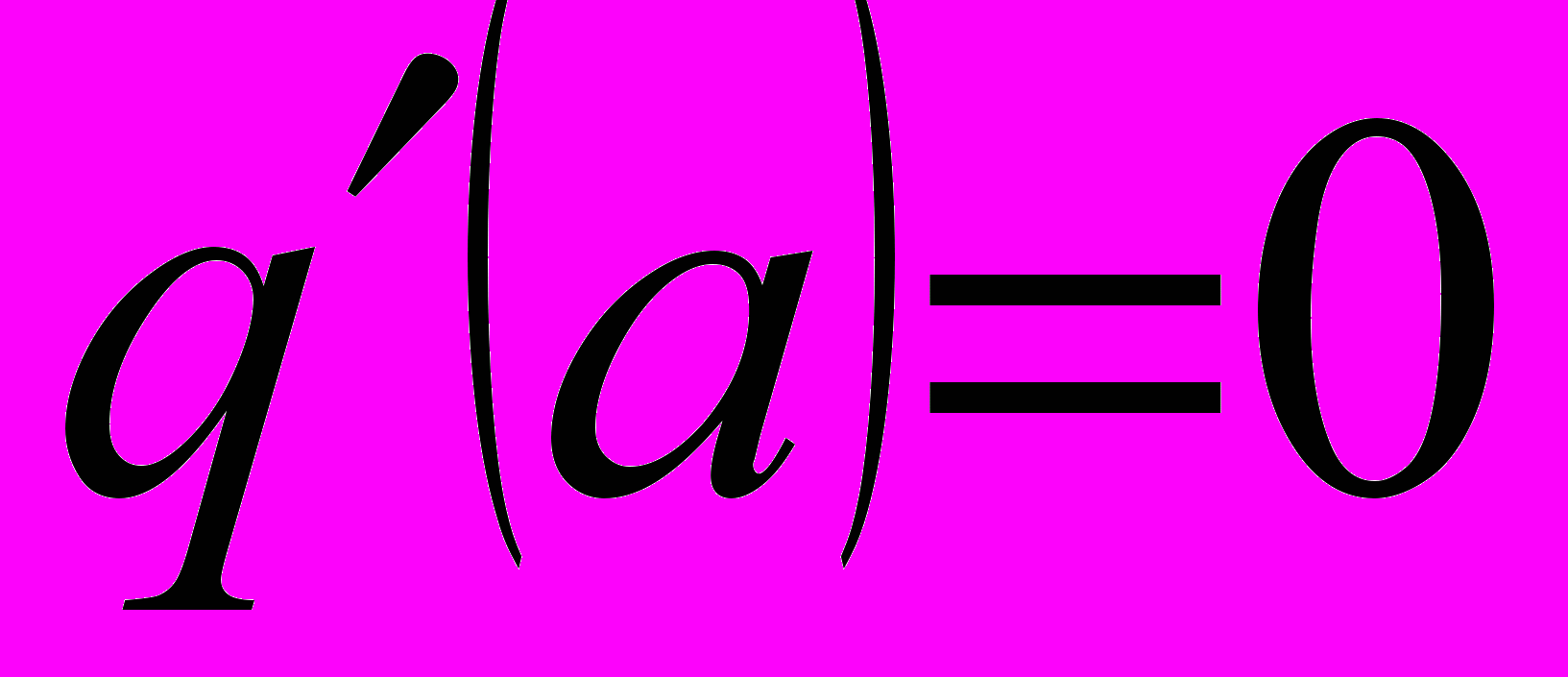 и уравнения (11) и (12) принимают вид
и уравнения (11) и (12) принимают вид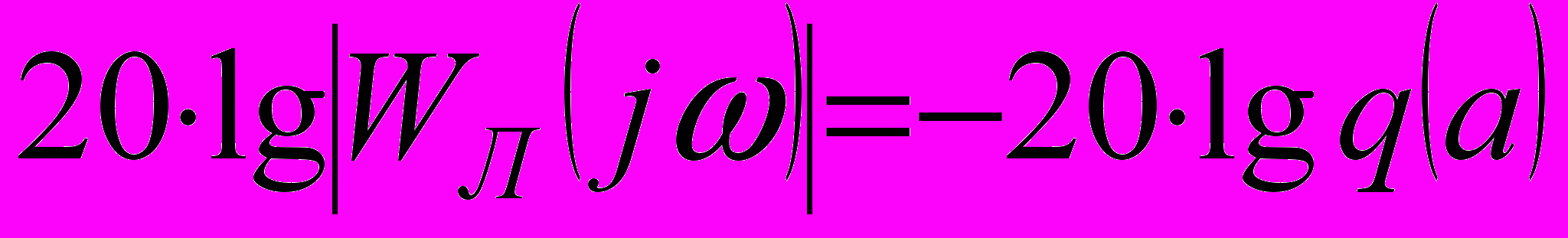 , (13)
, (13)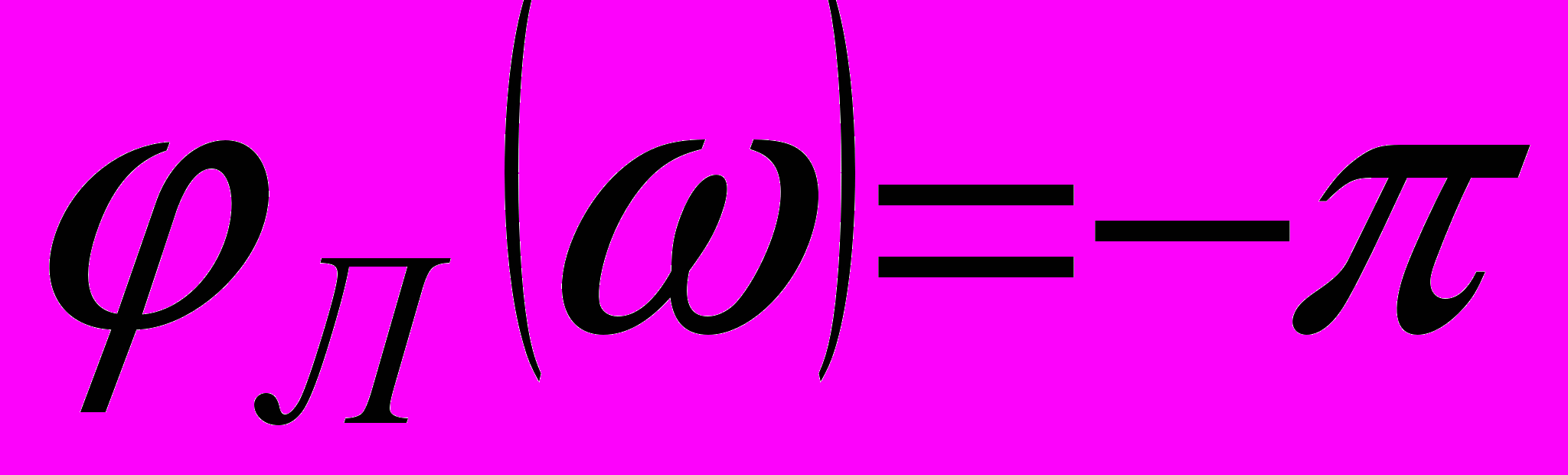 . (14)
. (14)Графическое решение показано на рисунке