Geum.ru

Програма до вступного іспиту з прикладної математики на окр магістра та спеціаліста

Вид материалаЗадача
Подобный материал:
ПРОГРАМА ДО ВСТУПНОГО ІСПИТУ
З ПРИКЛАДНОЇ МАТЕМАТИКИ
НА ОКР МАГІСТРА ТА СПЕЦІАЛІСТА
2012

1.Математичний аналіз


Межа функції (визначення по Коші і по Гейне). Визначення безперервності функції в точці. Теореми Вейєрштрасса і Больцано - Коші про функції, безперервних на відрізку. Рівномірна неперервність, теорема Кантора. Дифференційованіть і похідна дійсної функції дійсного змінного. Геометричний зміст похідної. Основні теореми про диференційовні функції (теореми Ферма, Ролля, Лагранжа). Формула Тейлора із залишком у формі Пеано, у формі Лагранжа. Визначення інтеграла Рімана. Інтегровність монотонних і безперервних функцій. Існування первісної у безперервної функції. Формула Ньютона - Лейбніца. Числові ряди. Основні ознаки збіжності (ознака порівняння, Даламбера. Коші, інтегральна ознака) для рядів з невід'ємними членами. Ознака Лейбніца. Поняття абсолютної та умовної збіжності.

2.Диференціальні рівняння


Задача Коші для диференціального рівняння першого порядку. Теорема існування та єдиності розв'язку задачі Коші. Лінійні однорідні звичайні диференціальні рівняння n-го порядку з постійними коефіцієнтами. Метод Ейлера. Лінійні неоднорідні звичайні диференціальні рівняння n-го порядку з постійними коефіцієнтами. метод Лагранжа

3.Рівняння математичної фізики


Формулювання крайової задачі Штурма-Ліувілля. Звести задачу Штурма-Ліувілля до інтегрального рівняння. Властивості власних значень і власних функцій задачі Штурма-Ліувілля. Довести теорему розкладання Стеклова. Функція Гріна одновимірної крайової задачі. (В чому відмінність від фундаментальної функції). Довести теорему єдиності для функції Гріна. Дати визначення самосопряженної крайової задачі. Довести симетричність функції Гріна для самосопряженної крайової задачі. Дати визначення фундаментальної та базисної систем рішень для одновимірної крайової задачі. Довести теорему існування для функції Гріна.

4.Теорія ймовірностей


Дискретне простір елементарних подій. Операції над подіями. Класичне визначення ймовірності. Властивості ймовірності. Умовні ймовірності. Незалежні події та їх властивості. Випадкові величини. Функція розподілу випадкової величини та її властивості. Числові характеристики випадкових величин: математичне сподівання, дисперсія та їх властивості. Ланцюги Маркова. Матриці переходу за один і к-кроків для однорідного ланцюга Маркова.

5.Функціональний аналіз


Лінійні оператори в лінійних нормованих просторах. Лінійне простір лінійних операторів (обмежених)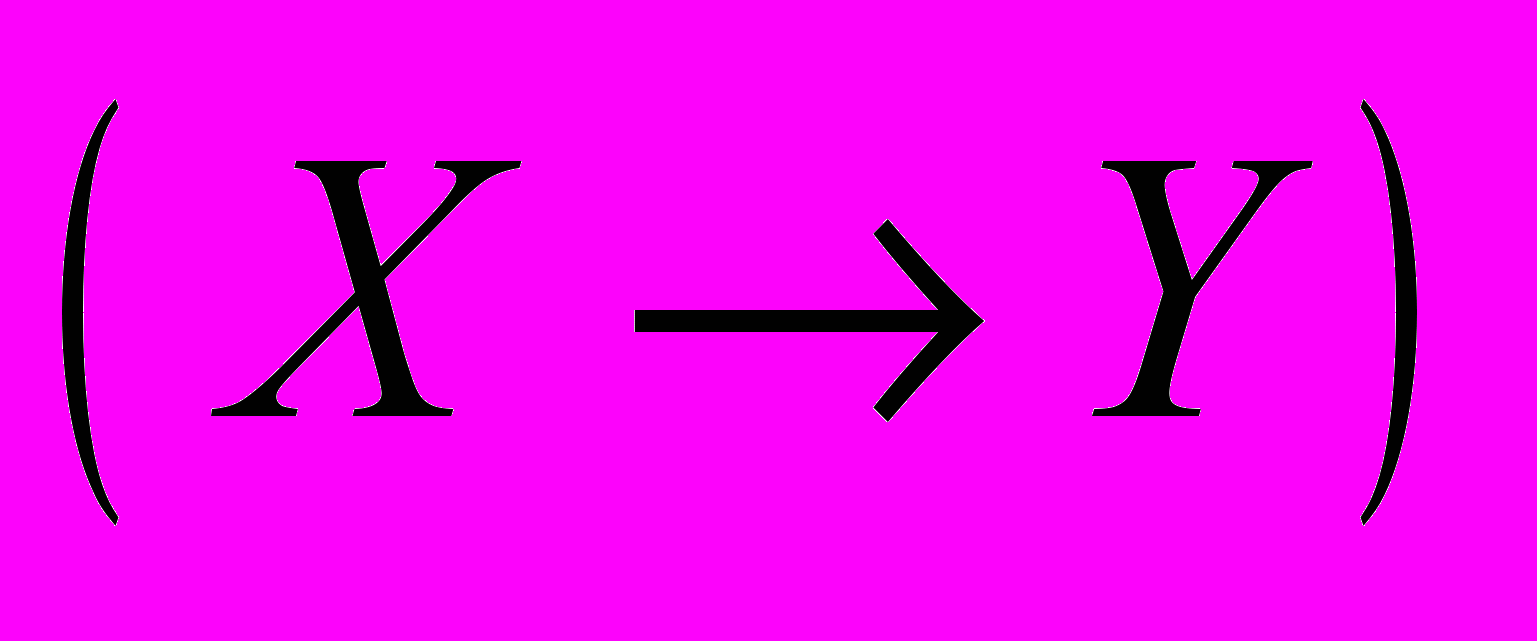. Абстрактні ряди Фурьє в Н. Теорема Рисса – Фішера. Теорема Гіильберта – Шмидта .

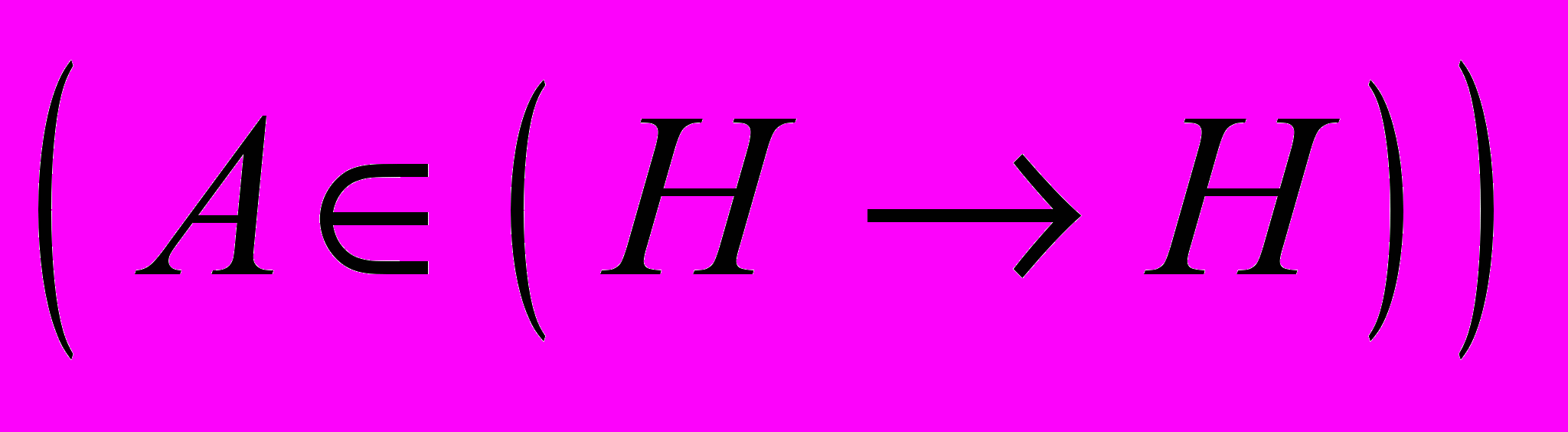6.Аналіз данних


Інформаційні та аналітичні моделі. Учасники процесу аналізу даних. Формалізація даних. Основні етапи KDD. Класи задач, що вирішуються методами Data Mining. Алгоритми Data Mining - асоціативні правила. Характеристики значущості асоціативного правила. Аналіз рядів динамік. моделі прогнозування.

7.Випадкові процеси


Випадкові процеси марківського типу. Рівняння Колмогорова. Процеси не залежать від майбутнього. Теорема Колмогорова-Прохорова. Тотожність Вальда. Коваріація та кореляція випадкового процесу. Взаємна коваріаційна і кореляційна функції випадкових процесів Похідна та інтеграл від випадкового процесу

8.Теорія функцій комплексної змінної


Інтегральна теорема Коши. Інтегральна формула Коши. Визначення лишку (вычета). Теорема про лишки. Обчислення лишку у разі полюса.

9.Обчислювальні методи


Теорема про LU-розкладання матриці. Метод Гауса. PLU-розкладання невиродженої матриці. Метод Гауса з частковим (повним) вибором головного елемента. Метод простої ітерації розв’язування СЛАР, необхідна й достатня умова збіжності. Метод Ньютона розв’язку нелінійних рівнянь. Інтерполяційний багаточлен Лагранжа. Залишковий член інтерполяційного багаточлена. Інтерполяційний багаточлен Ньютона з розділеними різницями. Залишковий член інтерполяційного багаточлена. Квадратурні формули Ньютона-Котеса (прямокутників, трапеції, Сімпсона).

10.Моделювання екологічних, економічних та соціальних процесів


Загальне уявлення про системний аналіз, як про методологічну основу вивчення систем.

Класифікація, типи і приклади моделей. Поняття стійкості в математиці та в екології.

11.Обчислювальна геометрія і комп’ютерна графіка


Розкладання в растр. Математична основа растрового розкладання в алгоритмі Брезенхема. Критерій ініціалізації пікселя в цьому алгоритмі. Алгоритми заповнення областей. Задача побудови кривих по контрольним точкам. Відсікання відрізків і багатокутників. Дискретизація зображень. Теорема Найквіста-Котельникова. Теорема Найквіста-Котельникова. Аліасінг зображень. Фільтрація зображень.

12.Теорія керування


Найпростіша задача термінального керування. Принцип максимуму Понтрягіна. Голчаста варіація. Приріст траєкторії і функціоналу на голчастою варіації (з доказом). Властивості функції Гамільтона вздовж екстремальних управлінь (одне з них з доказом). Оптимальне керування в лінійних системах. Керованість. Необхідна і достатня умова керованості. Екстремальні траєкторії.

13.Методи оптимізації


Завдання лінійного програмування: їх типи; поняття плану; графічне рішення ЗЛП.

Симплекс-метод для ЗЛП у стандартній формі. М-метод для ЗЛП в загальному вигляді.

Методи побудови початкового плану і метод його поліпшення: метод північно-західного кута; метод мінімального елемента; метод потенціалів. Ускладнені постановки ТЗ: обов'язкові і заборонені перевезення, обмеження на пропускну здатність, завдання зі складами, ТЗ в мережевий постановці. Основна теорема опуклого програмування Куна-Таккера (з доказом необхідності).

14.Системи та методи прийняття рішень


Теорія і практика раціонального виборів. Голосування и Прийняття колективного Рішення. Голосування більшістю голосів та методи підрахунку очок. Правило відносної більшості. Парадокс Голосування. Процедура Борда та її модіфікації. Процедура Кондерсе та її модифікації: правило Сімпсона, правило Копленда. Теорема Фішберна. Теорія і практика раціонального виборів. Властивості процедур Голосування - Основні аксіомі: оптимальність за Парето, анонімність, нейтральність, монотонність, Аксіома участі. Приклади процедур Голосування, які НЕ задовольняють аксіомам Голосування. Аксіомі К.Ерроу. Елементи Теорії Ігор. Основні означення та положення Теорії Ігор: учасники, Гравці, стратегії, виграш. Класифікація Ігор. Матричні ігри. Приклади и розв'язки матричних Ігор в чистих стратегіях. Домінування стратегій.

15.Теорія множин


Поняття множини. Способи завдання множин. Визначення підмножини. Рівність двох множин. Операції над множинами: об'єднання, перетин, різниця, доповнення. Декартів добуток множин. Висловлювання. Прості і складені висловлювання. Логічні зв'язки. Таблиці Куайна для логічних зв'язок. Характеристичні властивості логічних зв'язок. Алфавіт алгебри висловлювань. Індуктивне визначення формули алгебри висловлень (ФАВ). Інтерпретація ФАВ. Таблиці Куайна для ФАВ. Класифікація ФАВ: здійсненні, опровержімие, тотожно істинні, тотожно хибні формули.

16.Дискретна математика


Визначення графа. Способи завдання графів. Ізоморфізм графів. Маршрут, ланцюг, проста ланцюг. Цикл. Простий цикл. Цикломатичне число графа. Теорема про Цикломатичне числі. Визначення дерева. Визначення лісу. Теорема про ліси. Визначення булевой функції (БФ). Табличне завдання БФ. Елементарні БФ. Основні класи БФ. Двоїсті функції. Самодвойственной функції. Монотонні функції. Істотні і фіктивні змінні. лінійні функції.

17.Алгебра


Кільце многочленів над полем. Неприводимість над полем. Властивості неприводимих многочленів. Основна теорема про неприводими многочлени. Канонічне розкладання многочлена над полем. Корені многочлена. Теорема Безу. Кратні корені многочлена. Критерій кратності кореня. Основна теорема алгебри (б / д). Слідства з основної теореми для многочленів над полем Сі над полем R. Повна лінійна група. Оборотність матриць. Критерій оборотності. Скінченномірність. Базис і розмірність лінійного простору, властивості. Координати вектора в заданому базисі. Перехід до нового базису. Структура загального рішення однорідної СЛАР. Фундаментальна система рішень. Структура загального рішення неоднорідної СЛАР. Рівняння прямої і площини. Похідні види рівнянь. Взаємне розташування прямої і площини. Системи порівнянь першого ступеня. Китайська теорема про залишки. Порівняння по простому модулю. Квадратичні лишки. Символ Лежандра та його властивості. Квадратичний закон взаємності. Символ Якобі.

Первісні корені по заданому модулю. Теорема існування первісної кореня по простому модулю.

18.Програмне забезпечення обчислювальних систем


Поняття про клас і об'єкт. Статичні елементи класу. Інкапсуляція як основне властивість об'єктно-орієнтованого програмування. Спадкування як основне властивість об'єктно-орієнтованого програмування. Поліморфізм як основне властивість об'єктно-орієнтованого програмування.

19.Бази даних та інформаційні системи


Проблеми використання файлових систем. Поняття бази даних та її визначення. Призначення системного каталогу бази даних і його вміст. Діаграма "сутність-зв'язок». Поняття СУБД і її основні функції. Компоненти системи БД. Переваги та недоліки СУБД. Трирівнева архітектура ANSI-SPARC. Рівні опису даних та їх призначення. Підтримка принципу незалежності даних на основі багаторівневої архітектури. Моделі даних і концептуальне моделювання. Склад моделі. Категорії моделей. Об'єктні моделі. Моделі на основі записів. Коротка характеристика реляційної, мережевої та ієрархічної моделей даних. Архітектури многокорисувацьких СУБД. Телеобробка. Файл-серверна архітектура. Технологія «клієнт-сервер». Трирівнева архітектура. Багаторівневі архітектури. Розподілені системи. Реляційна модель даних. Математичні визначення домену, відносини, кортежу, атрибута, ступеня і кардинального числа. Визначення реляційної бази даних. Властивості відносин.

20.Архітектура обчислювальних систем


Поняття про архітектуру персонального комп'ютера. Загальна характеристика сімейства мікропроцесорів Intel. Реальний і захищений режими. Регістри мікропроцесора, і їх призначення. Сегментні регістри. Регістр прапорів. Стек, його призначення. Структура асемблерних програм. Директиви організації програмних сегментів. Формати операторів асемблера. Константи, змінні і мітки. Представлення інформації в поле операндів. Директиви визначення даних і розподілу пам'яті. Команди організації переривань. Переривання BIOS і DOS. Основні функції переривань INT 10H, INT 21H. Організація вводу-виводу. Висновок на екран в текстовому режимі. Організація введення з клавіатури. Команди управління мікропроцесором.

21.Програмування


Класифікація підпрограм. Поняття параметрів, їх класифікація. Формальні та фактичні параметри, способи передачі параметрів. Керуючі структури. Класифікація базових структур. Властивості базових структур. Поняття оператора в мові С + +. Реалізація керуючих структур. Конструюються типи даних. Масиви. Записи. Особливості реалізації в мовах програмування. Робота з покажчиками. Динамічне виділення пам'яті. Динамічні масиви. Створення динамічного масиву. Методи внутрішнього сортування. Оцінка кожного з методів. Використання сортування злиттям в якості внутрішнього сортування. Чіткий подання даних у пам'яті. Основні процедури та функції для роботи з ланцюжками. Побудова односпрямованих ланцюжків. Побудова двонаправлених ланцюжків. Основні процедури та функції для роботи з двонаправленими ланцюжками.

22.Архітектура комп’ютерних мереж


Архітектура мережної моделі OSI. Описати рівні і виконувані завдання. Загальна структура пакета даних. Архітектура стека протоколів TCP \ IP і його відповідність моделі OSI. Охарактеризувати вимоги до адрес в комп'ютерних мережах. Апаратні, числові та символьні адреси. Структура, класи IP-адрес і спеціальні IP-адреси, поняття маски IP-адреси, привести приклад маски підмережі. Централізовані і приватні (автономні) IP-адреси. Алгоритм динамічного призначення IP-адрес, протокол DHCP. Поняття кордону мережі і шлюзу. Технологія NAT як спосіб підключення до глобальної мережі.

23.Логічні алгоритми і системи штучного інтелекту


Структура інтелектуальної обчислювальної системи. Поняття знання. База знань (БЗ). Концептуальний і інформаційний рівні БЗ. Модель предметної області і мову подання знань. Основні ознаки знань і даних. Інтелектуальні пакети прикладних програм (ІППП). Основні компоненти ІППП і схема функціонування. Модель предметної області ІППП у вигляді функціональної семантичної мережі. Робота планувальника завдань ІППП на основі алгоритму паросполучення. Моделі подання знань: семантичні мережі (СМ). Типові об'єкти СМ і фундаментальні типи зв'язків (відносин). Спадкування властивостей в СМ. Транзитивні відносини. Процедурні СМ. Процедури виведення на семантичних мережах.

24.Теорія програмування


Загальна схема програм пошуку по графу. Приклади інтерпретації. Матроіди. Загальна схема і приклади реалізації жадібних алгоритмів. Зв'язок матроіда і жадібних алгоритмів. Принципи і прийоми динамічного програмування. Приклади схем програм реалізації динамічного програмування

Література

  1. Абель П. Язык ассемблера для IBM PC и программирования.
  2. Ахо А., Хопкрофт Д., Ульман Д. Структуры данных и алгоритмы.
  3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы.
  4. Вирт Д. Алгоритмы и структуры данных.
  5. Воеводин В.В. Линейная алгебра.
  6. Габасов Р.Ф. Методы оптимизации.
  7. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика.
  8. Дейт К. Ведение в системы баз данных.
  9. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ .
  10. Кормен Т., Лайзерсон Ч., Ривест Р., Штайн К., Алгоритмы. Построение и анализ.
  11. Крушевский А.В., Теория игр. – К., 1977 – 213 с.
  12. Ларичев О.И. Наука и искусство принятия решения.
  13. Любимский А.В., Трифонов С.А. Программирование.
  14. Матвеев Н.М., Методы интегрирования обыкновенных дифференциальных уравнений.
  15. Представление и использование знаний. (Под ред. Х. Уэно, М. Исудзука).
  16. Самарский А.А., Гулин А.В. Численные методы.
  17. Страуструп Б. Язык программирования C++.
  18. Таненбаум Э. Современные операционные системы.
  19. Таха X. Введение в исследование операций.
  20. Яблонский СВ. Введение в дискретную математику.