Задачи по теме Высокочастотные
| Вид материала | Лекция |
- Урок информатики по теме, 49.9kb.
- Урок в форме соревнования между тремя колонками по теме, 137.47kb.
- Задачи моего диплома: Найти и прочитать материал по моей теме, 57.25kb.
- Задачи : Учебная : Углубление, обобщение и систематизация знаний по программному обеспечению, 73.29kb.
- Задачи : Подобрать литературу по данной теме. Оформить конспекты по данной теме, 85.88kb.
- БиномНьютон а, 123.16kb.
- Задачи: Подобрать литературу по теме «Золотое сечение». Найти информацию по теме, 164.44kb.
- Задачи : 1 проверить знания по теме: Отряды млекопитающих: Парнокопытные и Непарнокопытные., 107.2kb.
- Задачи: Повторить основные понятия логики. Решить задачи: на построение логических, 274.05kb.
- Задачи семинара: расширить представление о роли сельского хозяйства в мировой экономике, 44.28kb.
Задачи по теме Высокочастотные асимптотики для уравнения Гельмгольца в неоднородной среде | ||
Лекция от 30 ноября 2011 г. | ||
| Номер | Формулировка | коммент |
| 1 | Найти эйконал для двумерного уравнения Гельмгольца в неоднородной среде 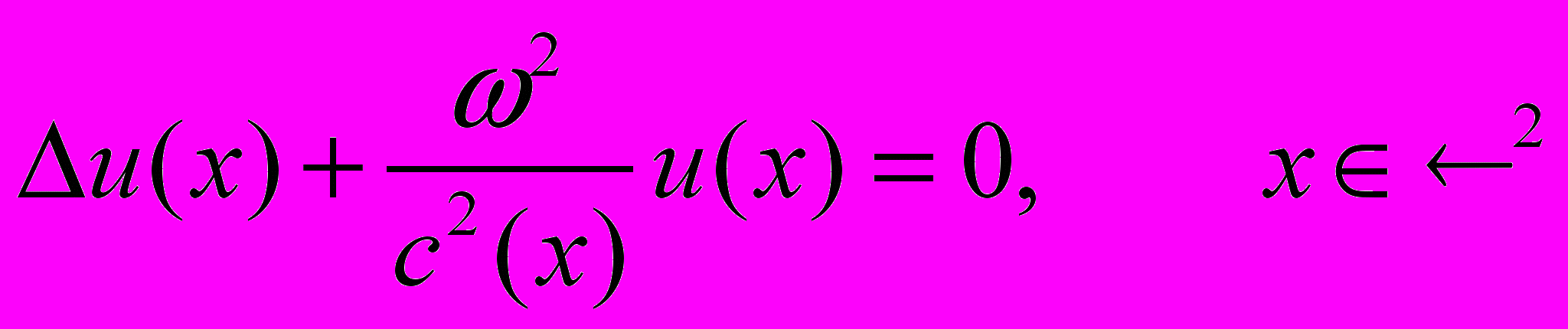 при при 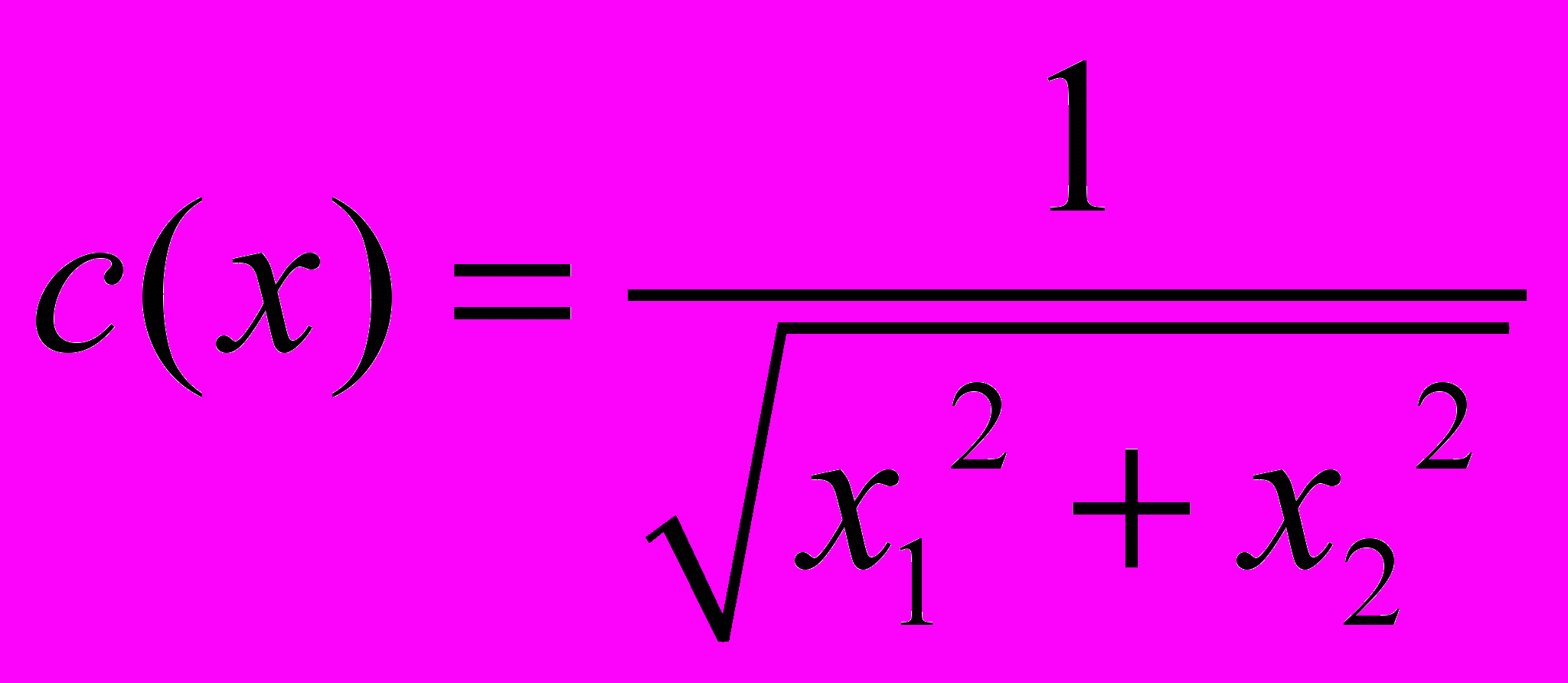 . . | Решение смотри ниже |
| 2 | Найти уравнения лучей для двумерного уравнения Гельмгольца в неоднородной среде 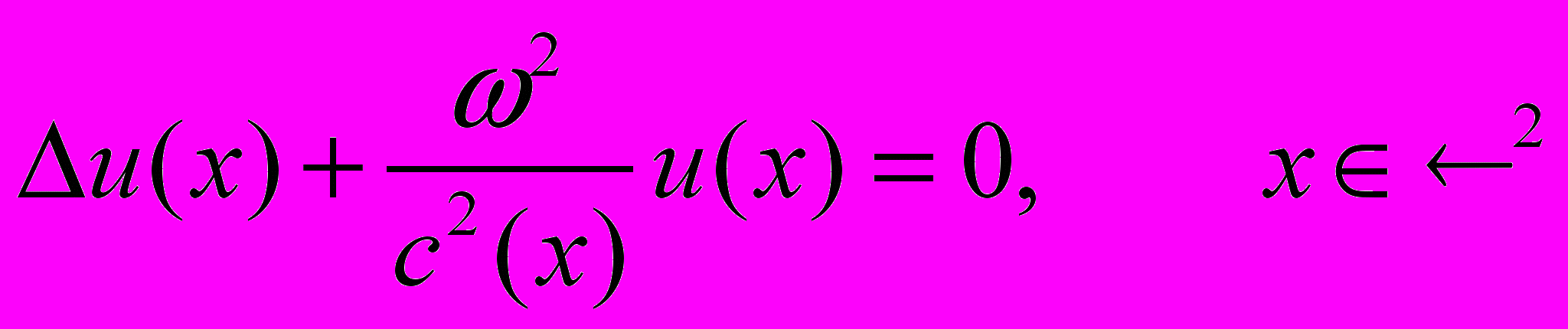 при при 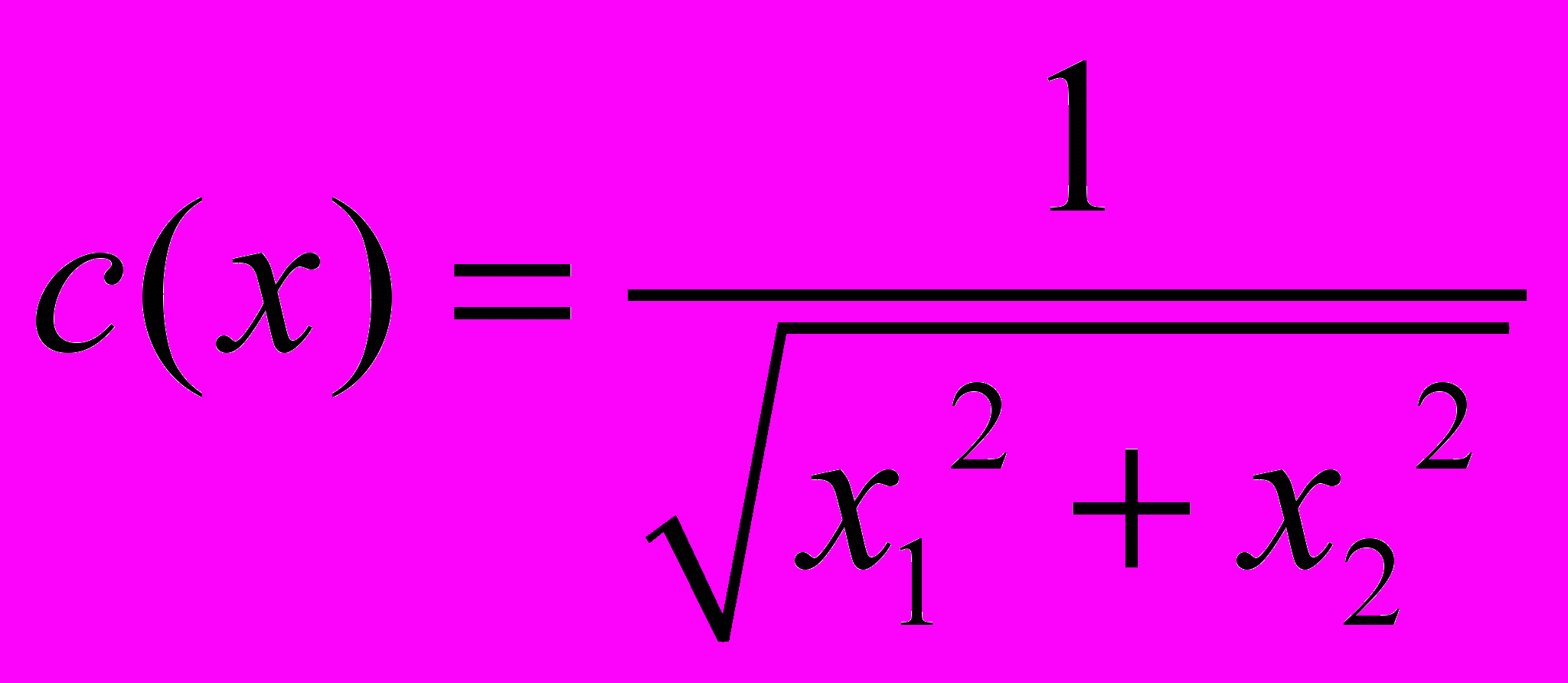 . . | Решение смотри ниже |
| 3 | Найти эйконал для двумерного уравнения Гельмгольца в неоднородной среде 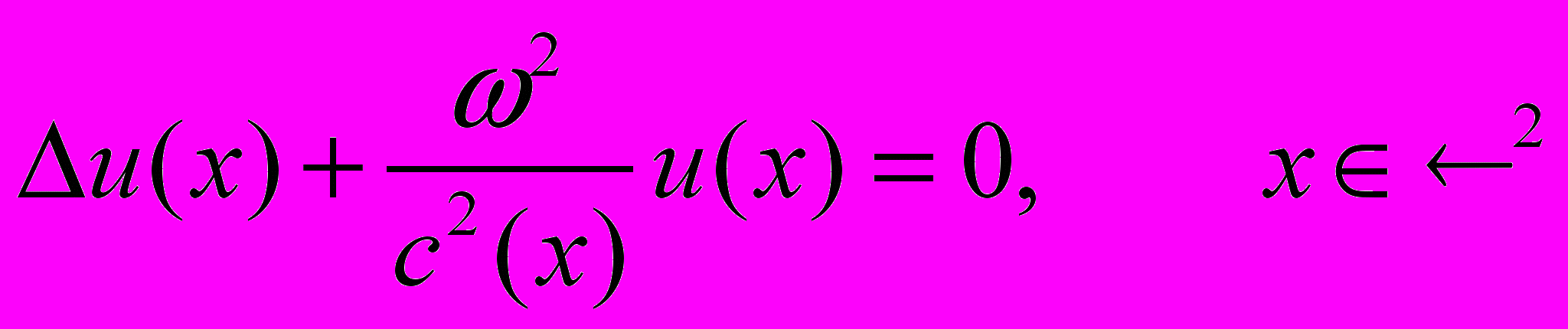 при 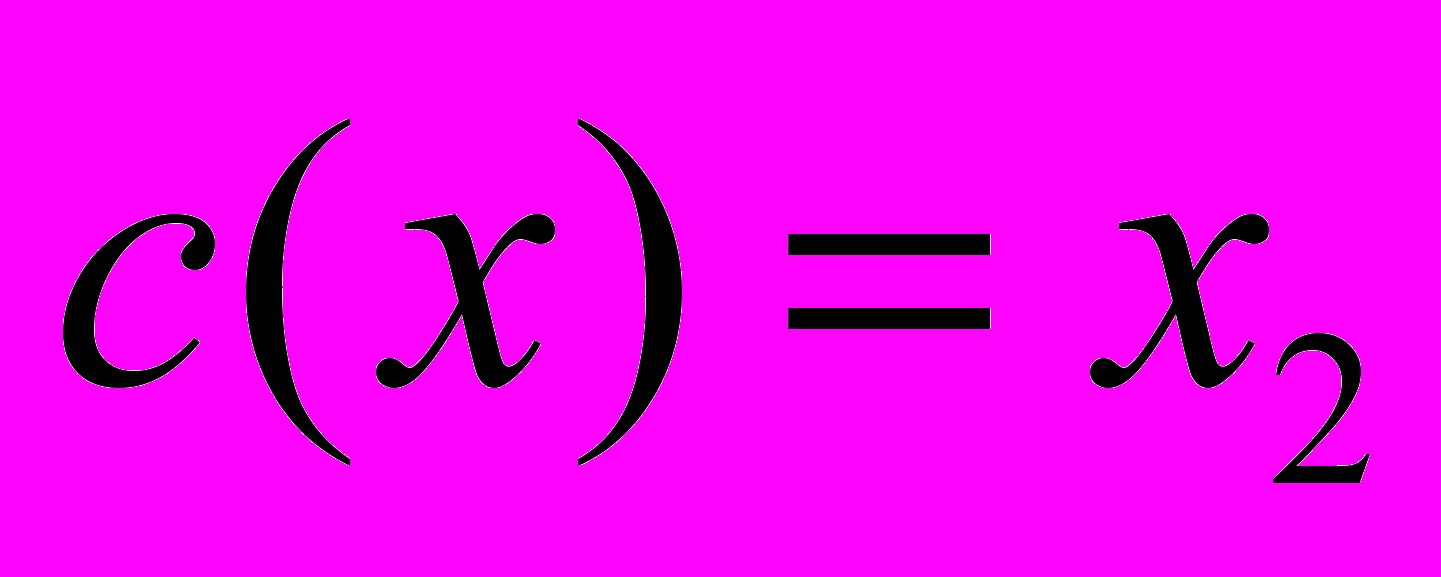 . . | |
| 4 | Найти уравнения лучей для двумерного уравнения Гельмгольца в неоднородной среде 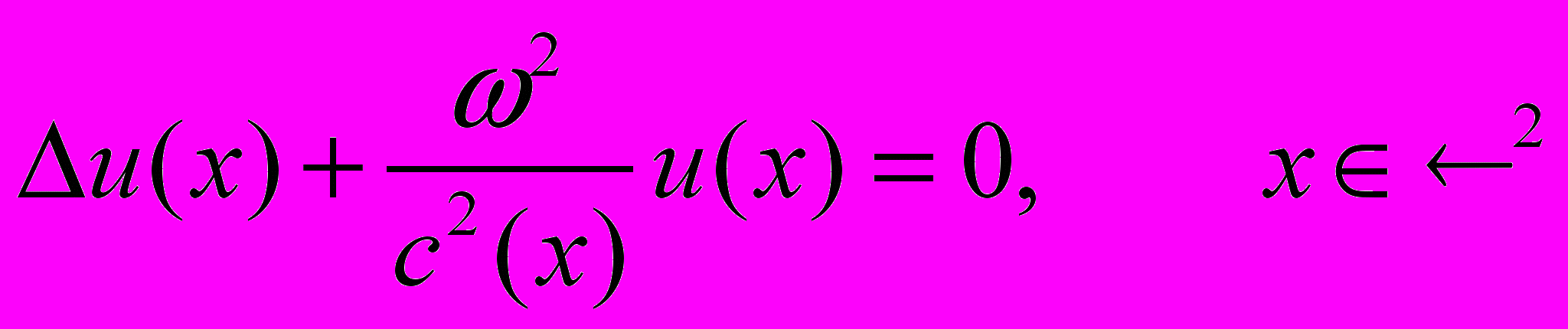 при 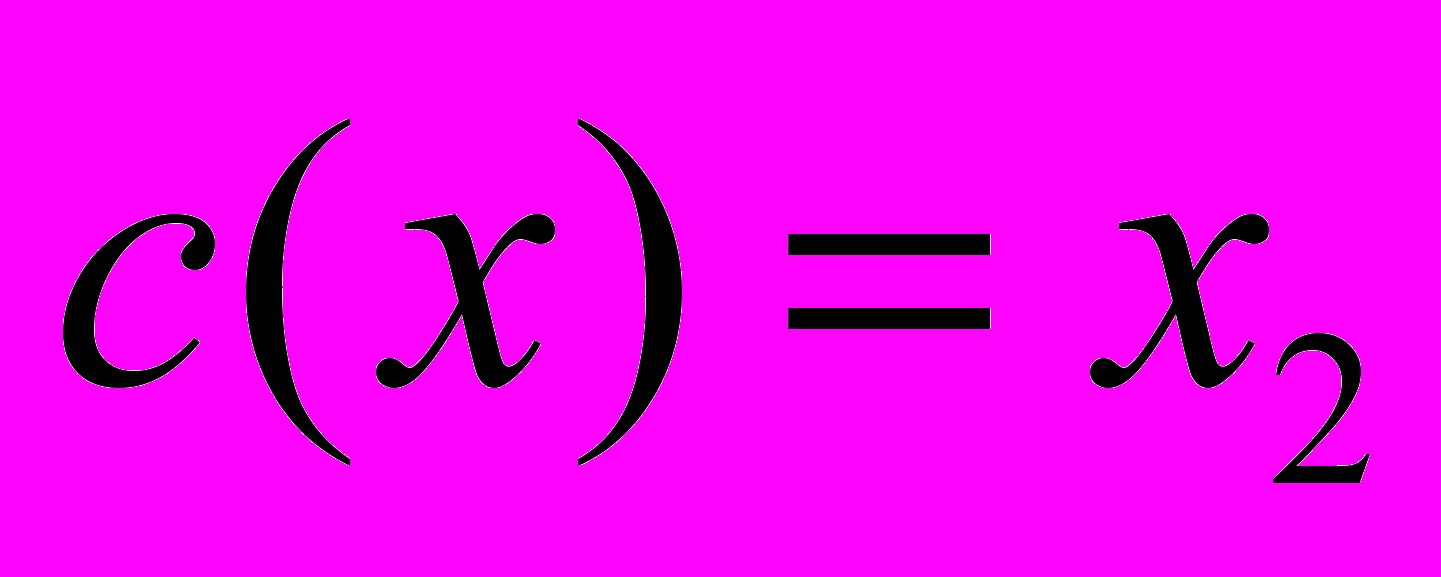 . . | |
| 5 | Найти эйконал для двумерного уравнения Гельмгольца в однородной среде 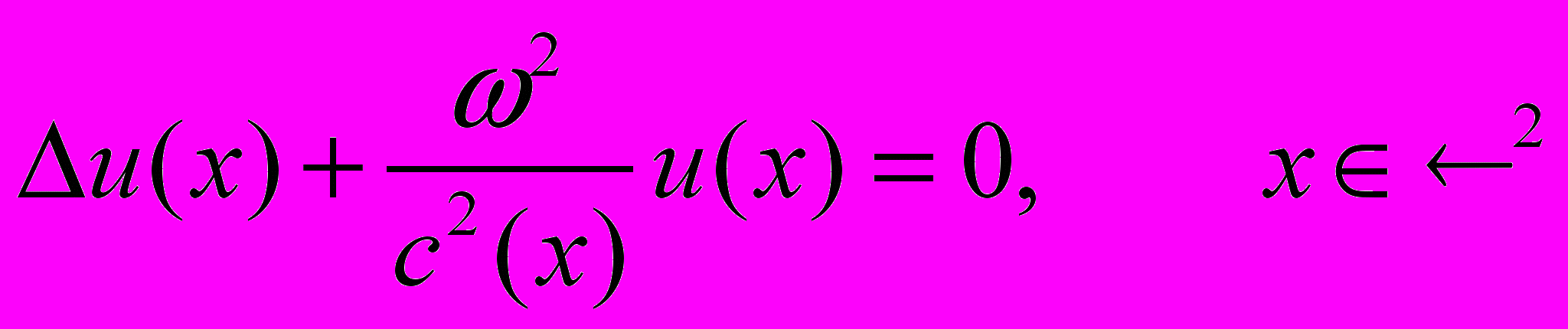 при. 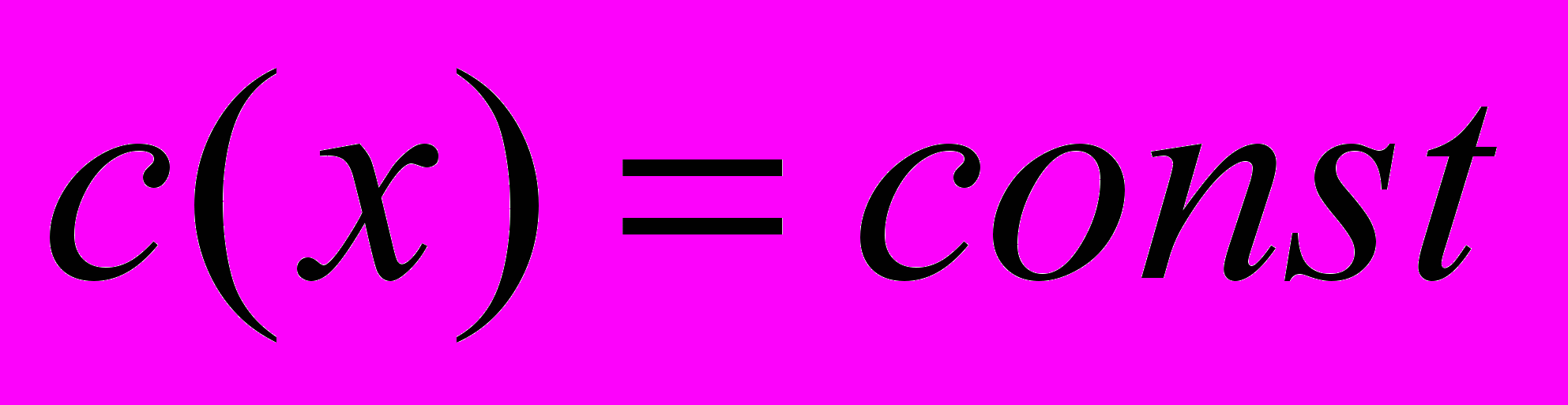 | |
| 6 | Найти уравнения лучей для двумерного уравнения Гельмгольца в однородной среде 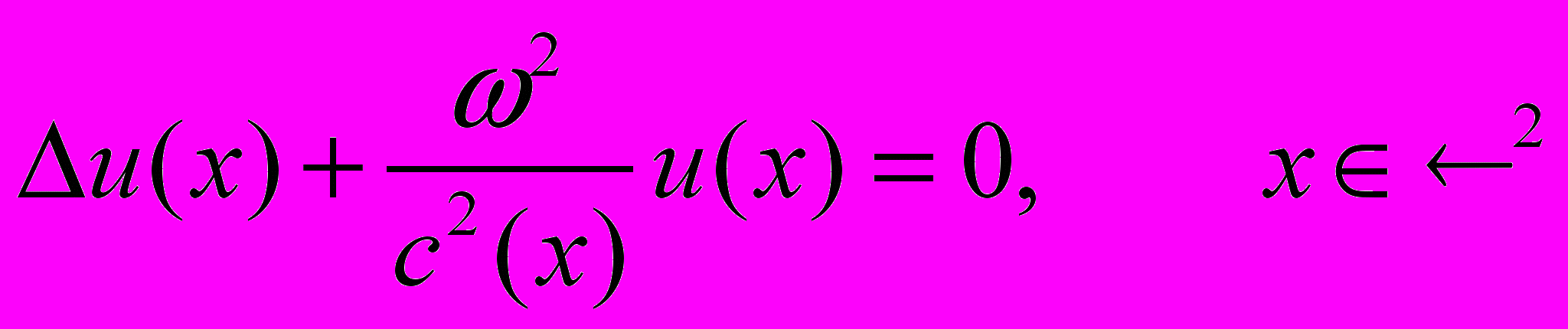 при 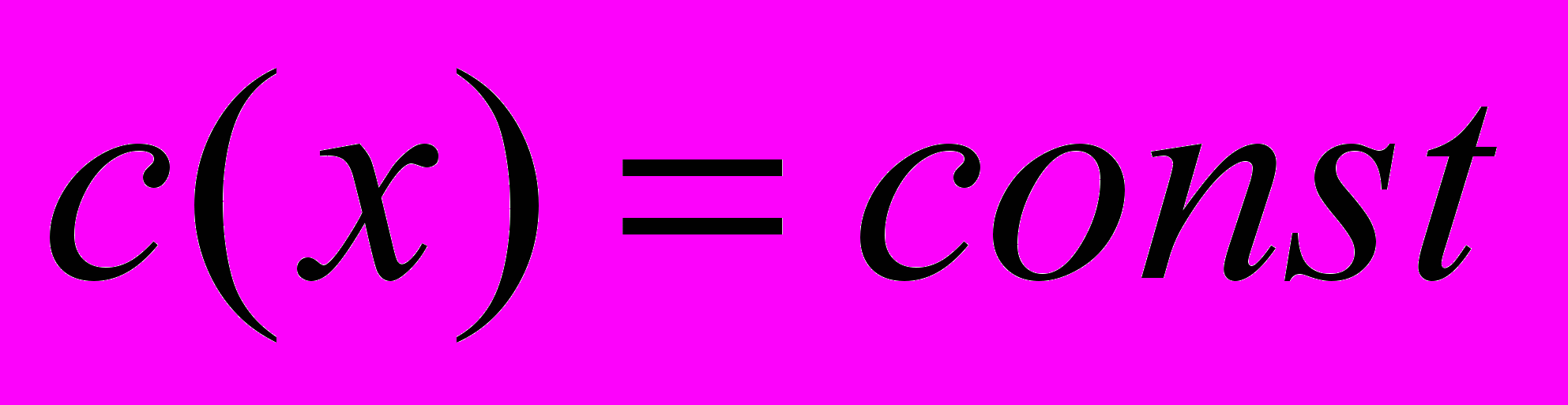 . . | |
_____________________________________________________________________________
Задача 1: Найти эйконал для двумерного уравнения Гельмгольца в неоднородной среде
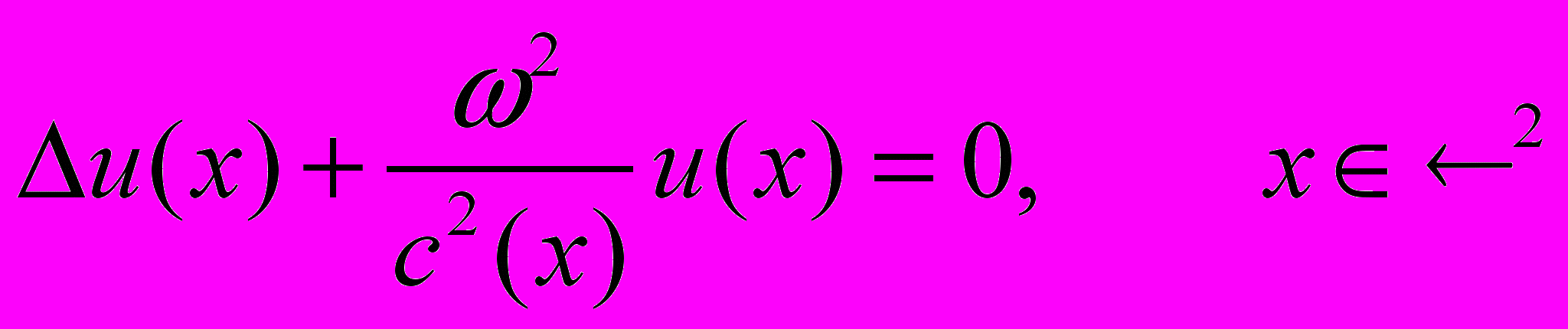 при
при 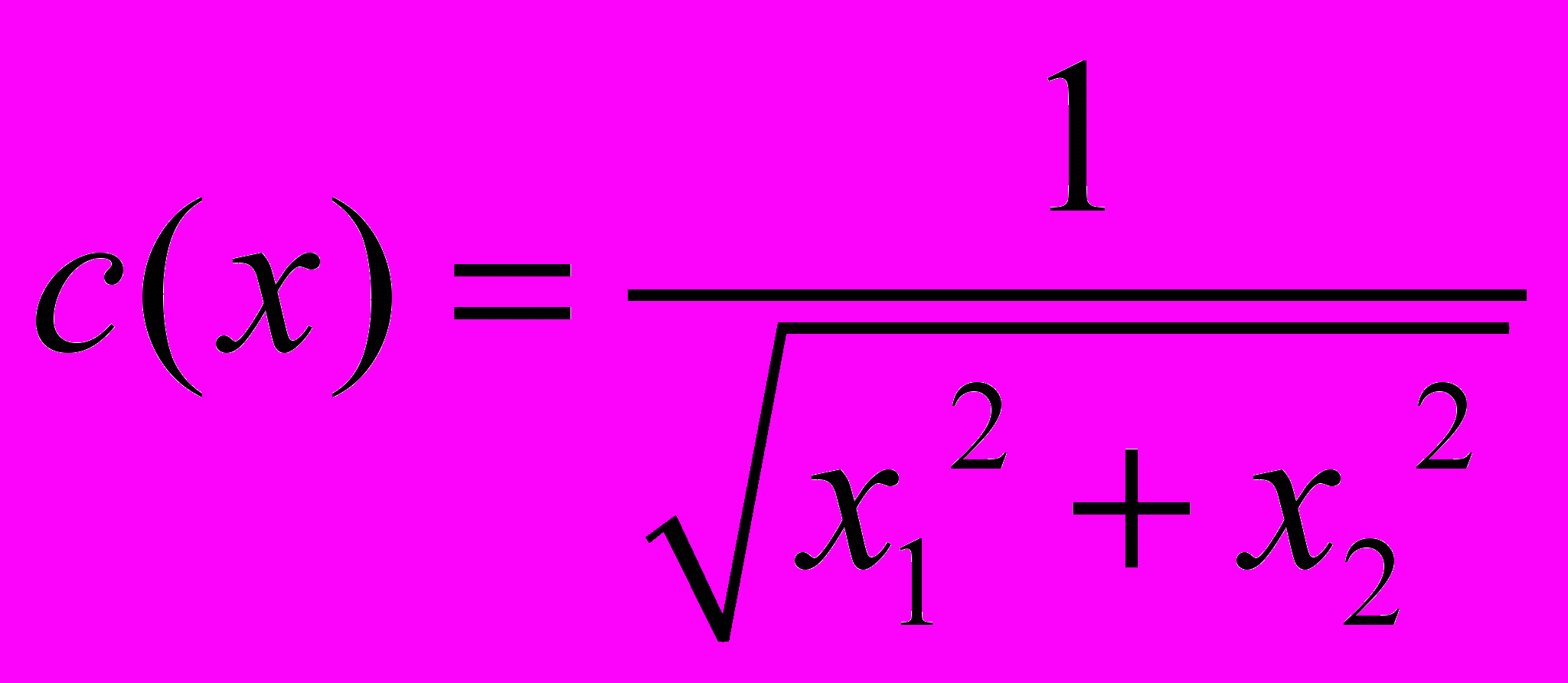 .
.Указание: выписать уравнение Гамильтона-Якоби для функционала Ферма
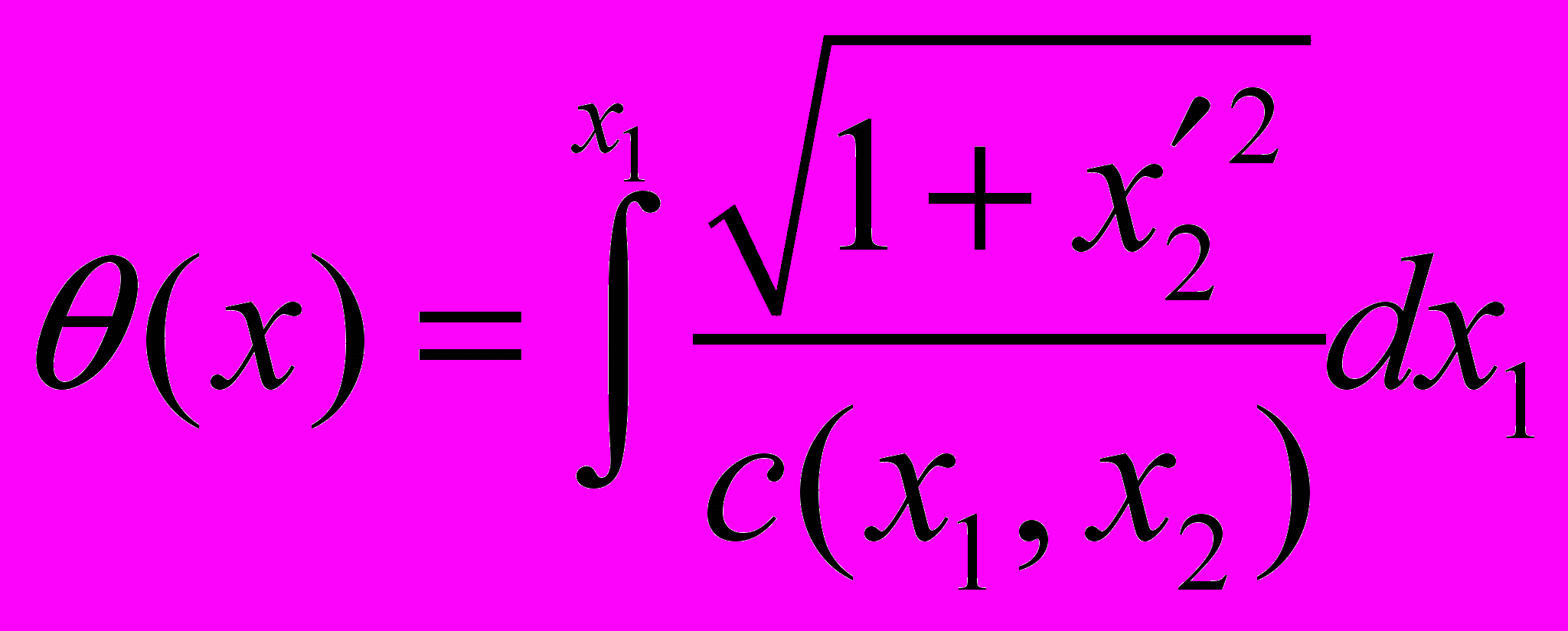 ,
,и решить его методом разделения переменных.
Решение:
Введем новые обозначения:
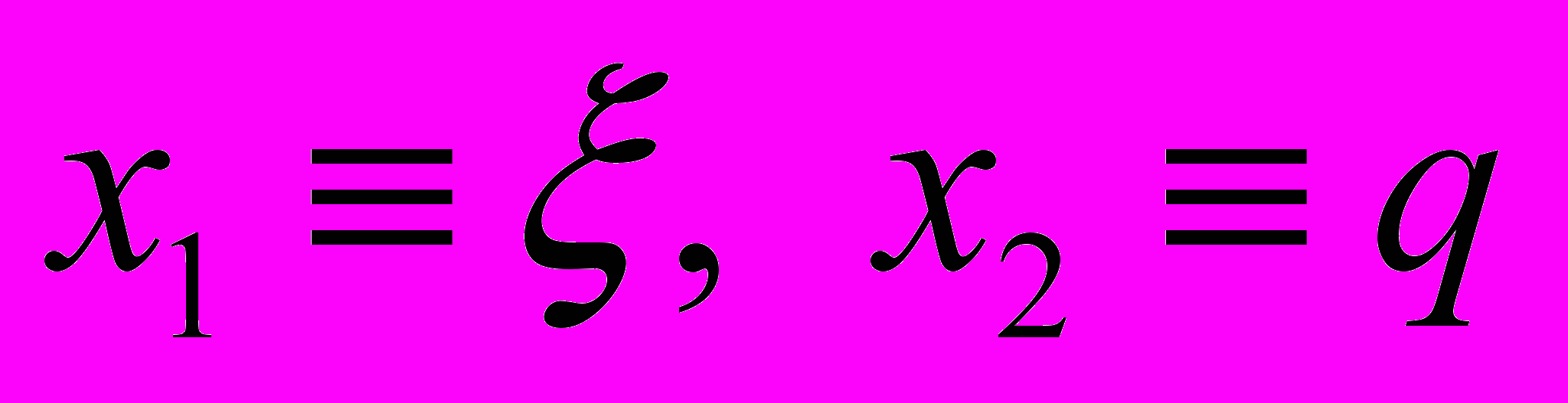 и вычислим преобразование Лежандра от функции
и вычислим преобразование Лежандра от функции 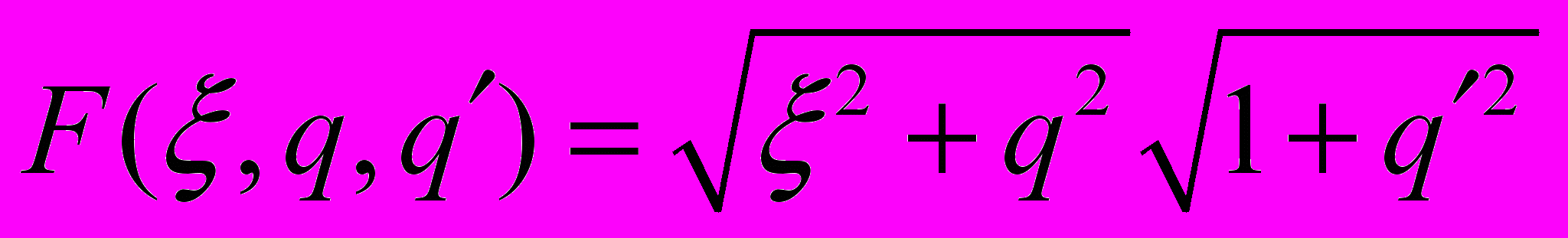 по переменной
по переменной 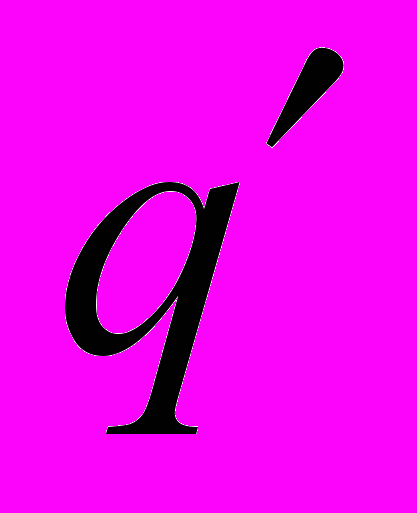 :
: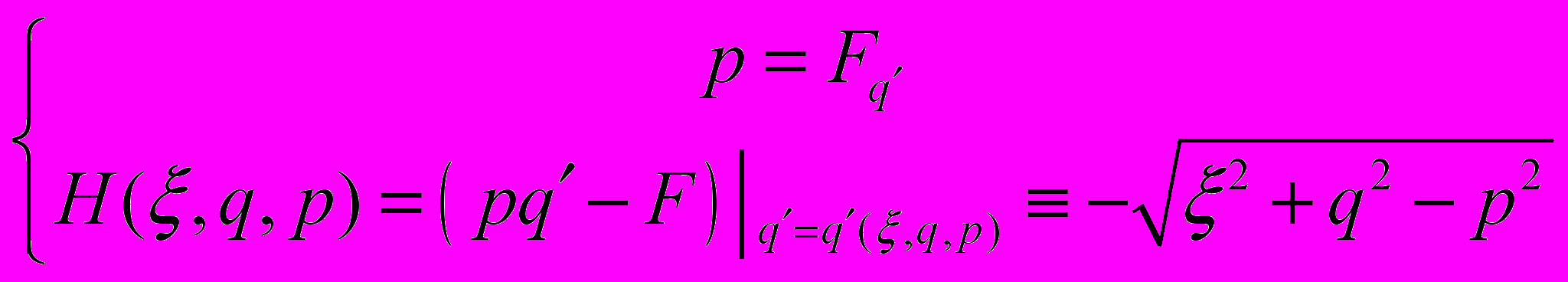
Уравнение Гамильтона-Якоби имеет вид
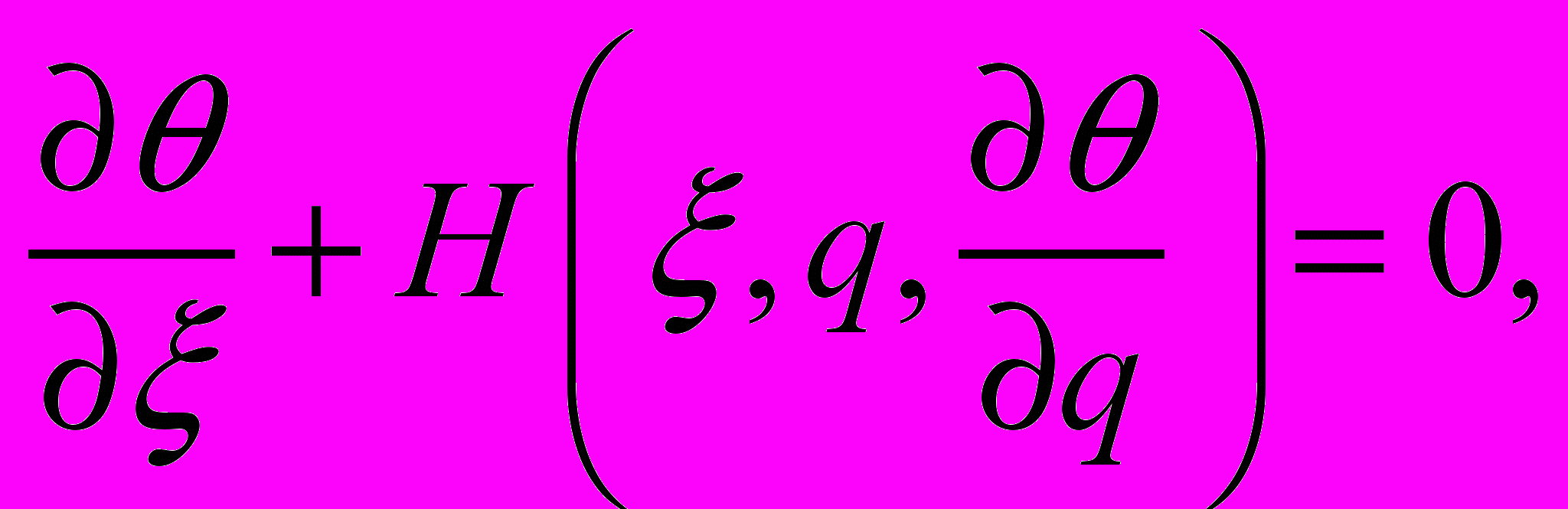
где
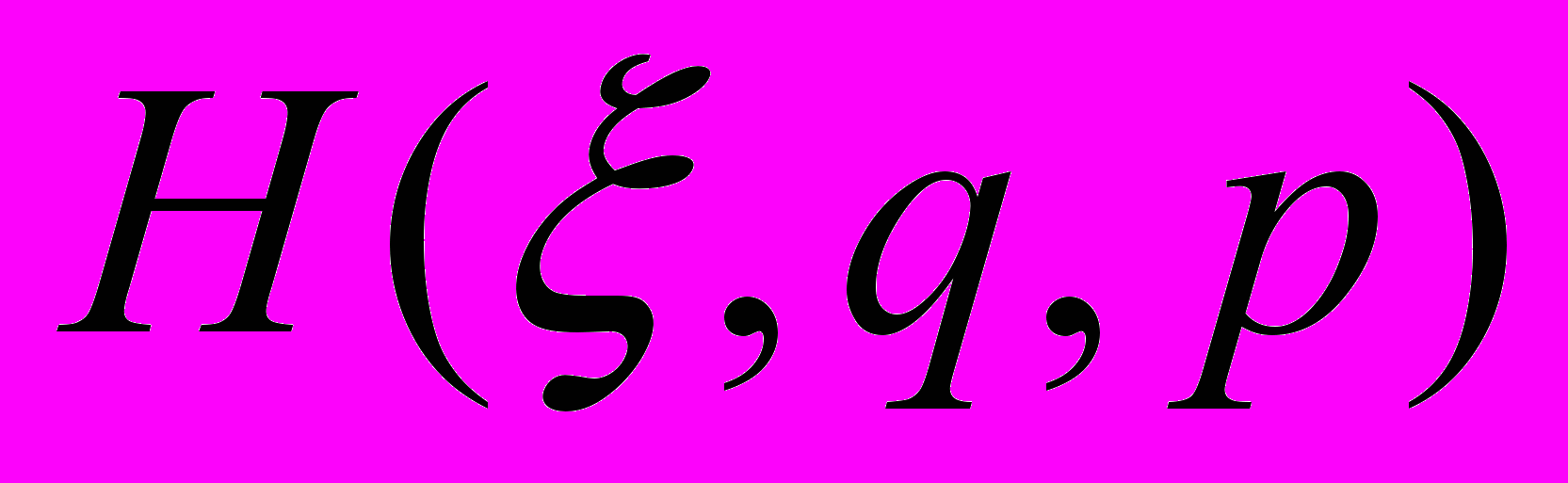 полученная выше функция Гамильтона, то есть
полученная выше функция Гамильтона, то есть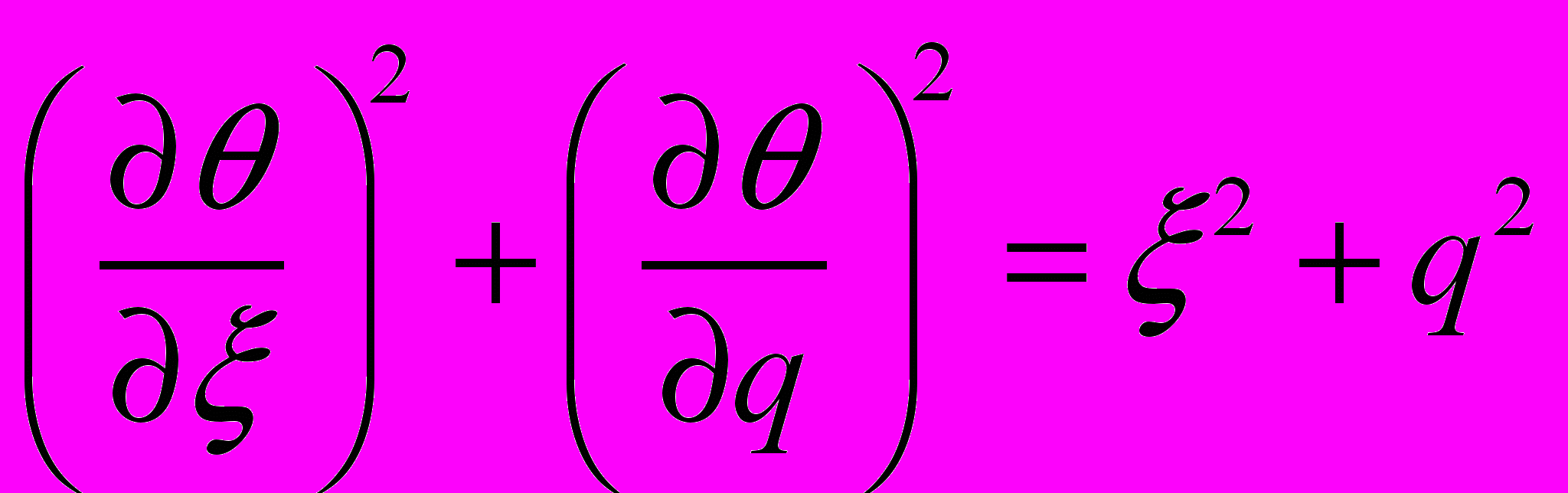 .
.Таким образом, для функционала Ферма уравнение Гамильтона-Якоби является уравнением эйконала и имеет вид
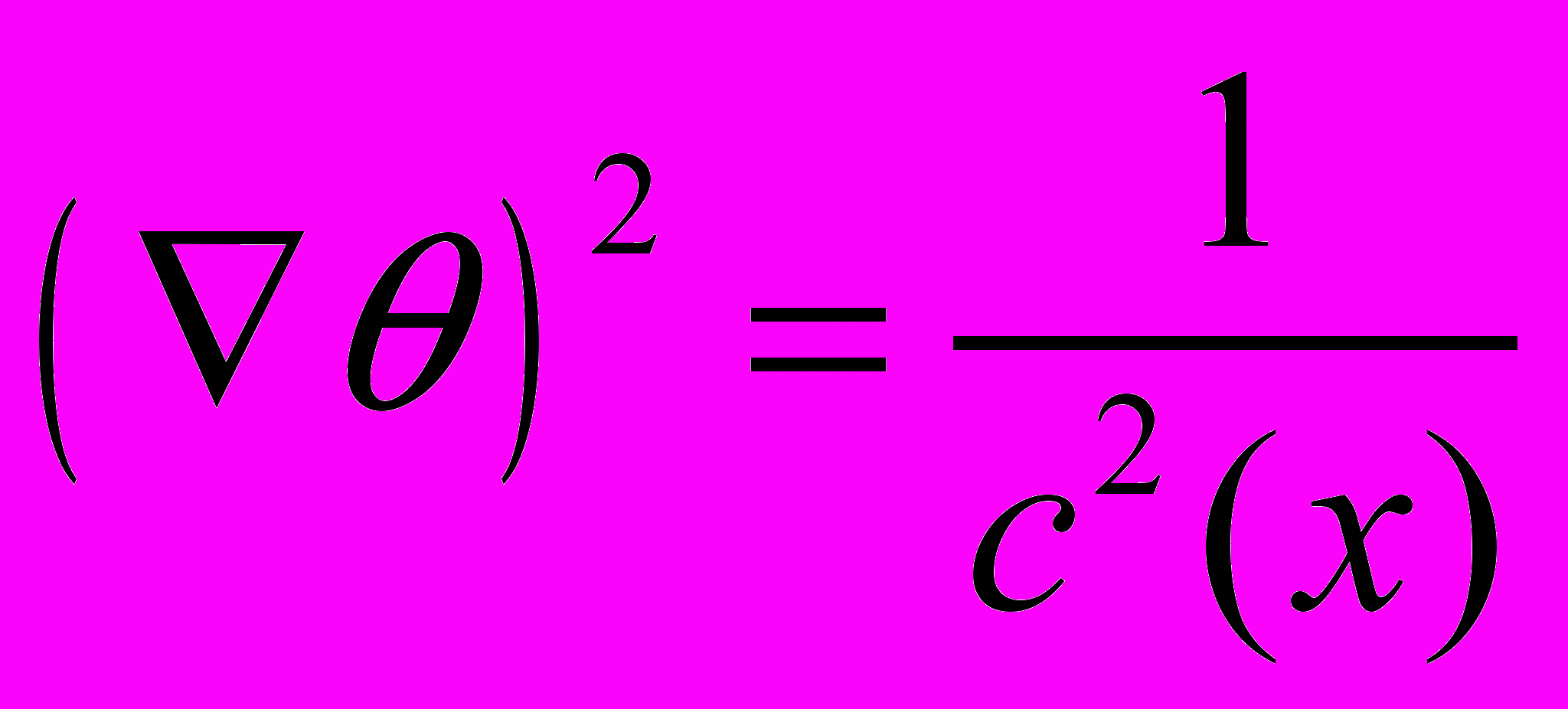 . Решаем полученное уравнение методом разделения переменных и ищем решение в виде:
. Решаем полученное уравнение методом разделения переменных и ищем решение в виде: 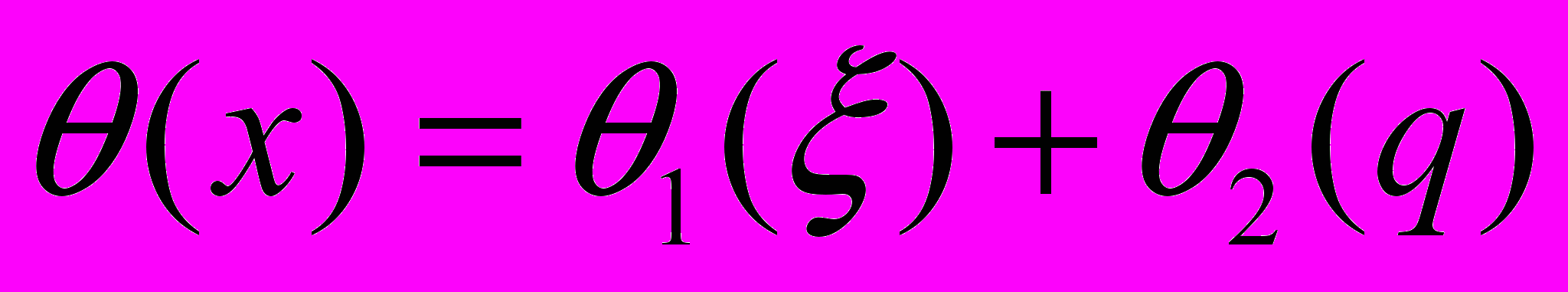 . Обозначая через
. Обозначая через  постоянную разделения переменных, получаем
постоянную разделения переменных, получаем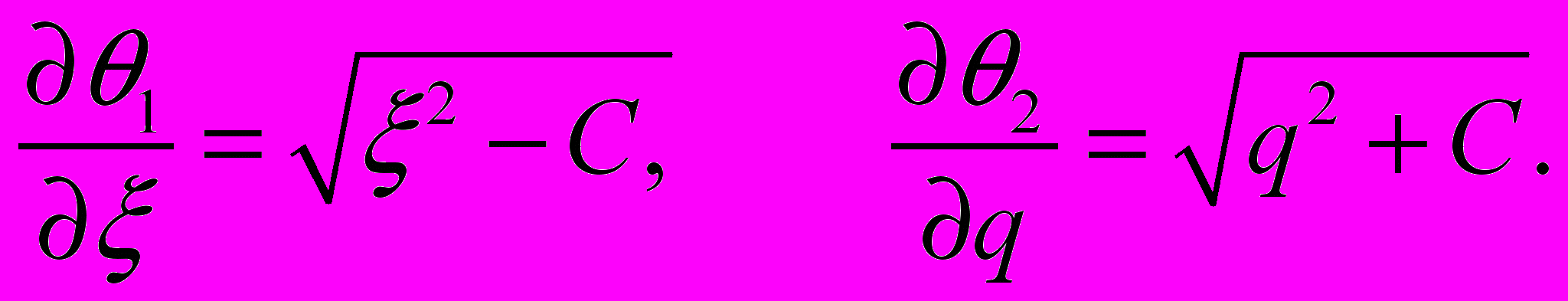
Возвращаясь к исходным переменным
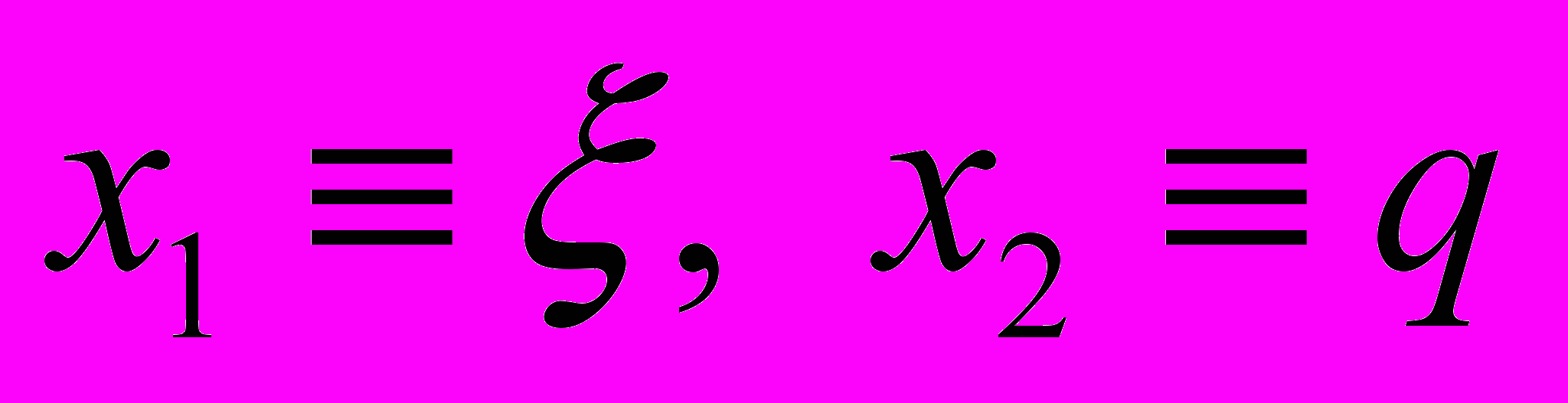 , имеем
, имеем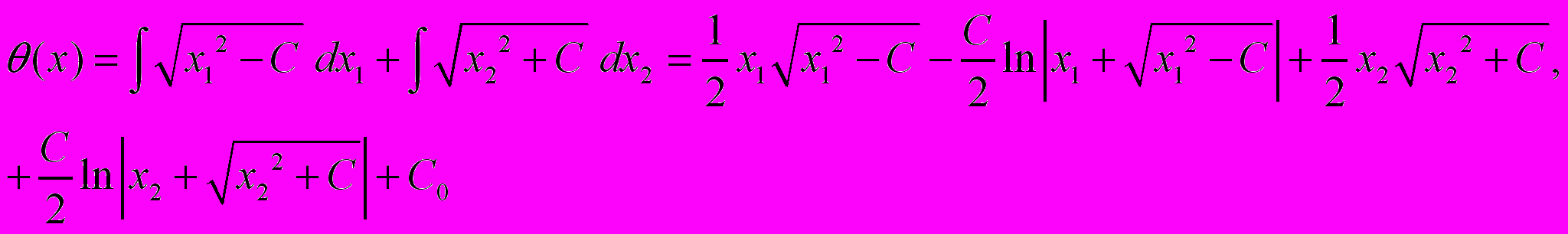
__________________________________________________________________
Задача 2: Найти уравнения лучей для двумерного уравнения Гельмгольца в неоднородной среде
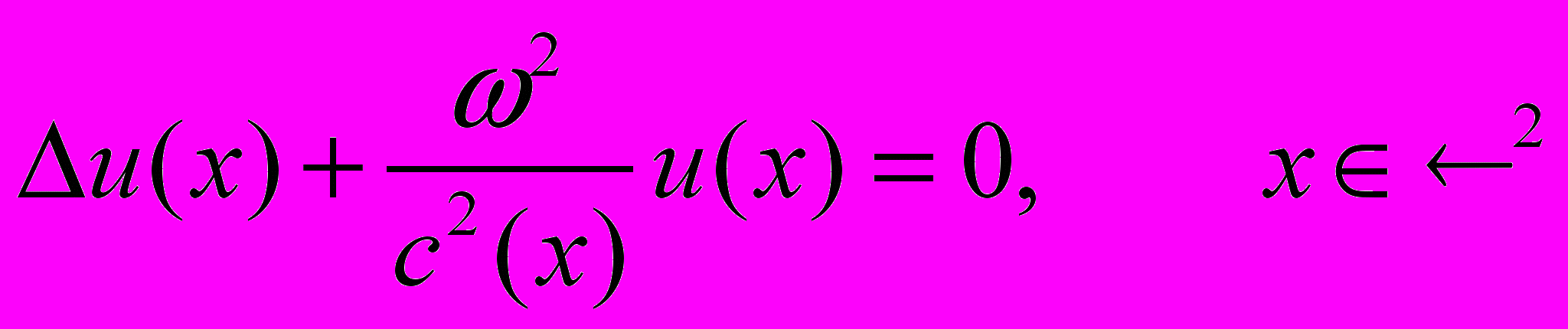
при
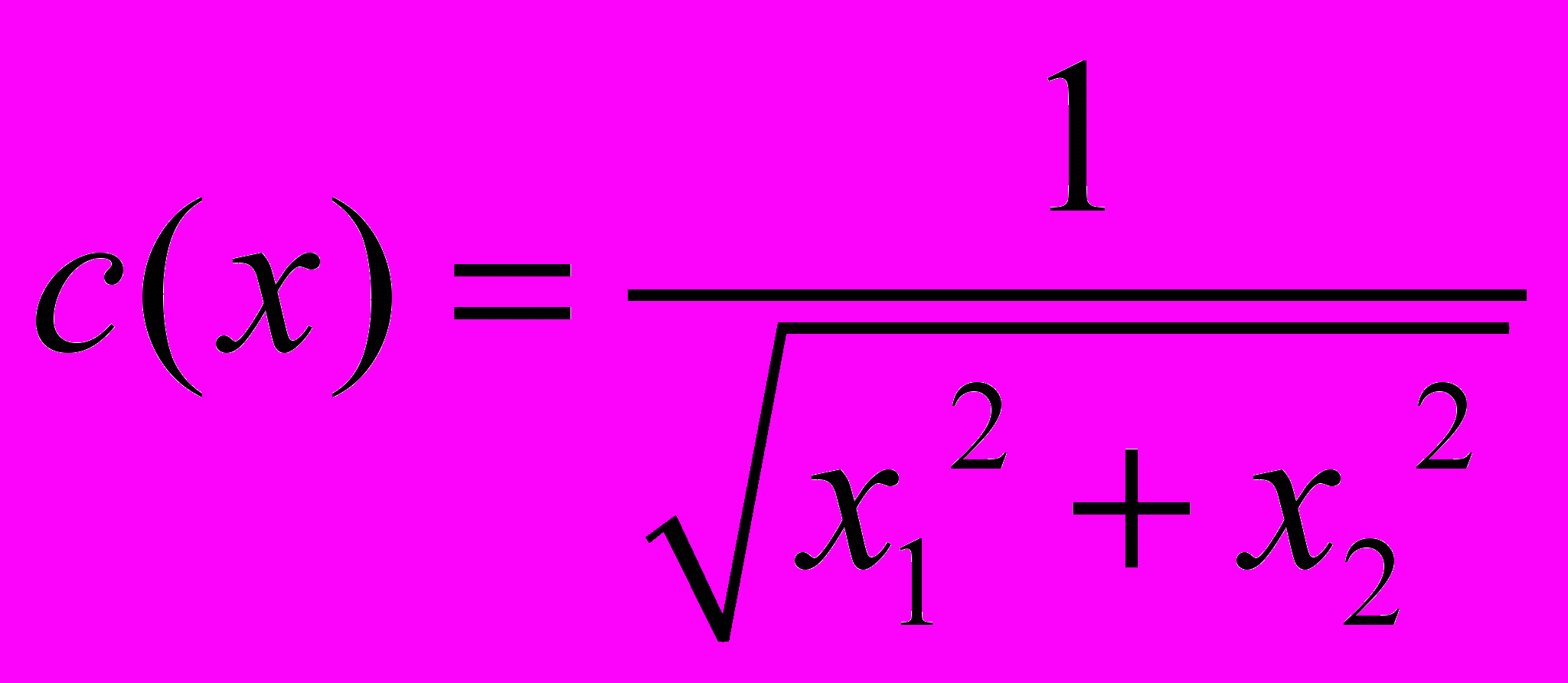 .
.Указание: Выписать уравнение эйконала. Применить к нему метод разделения переменных. Написать общее решение в квадратурах, зависящее от постоянной разделения переменных
 . Уравнения лучей (т.е. экстремалей функционала Ферма) можно найти на основании теоремы Якоби из соотношения
. Уравнения лучей (т.е. экстремалей функционала Ферма) можно найти на основании теоремы Якоби из соотношения 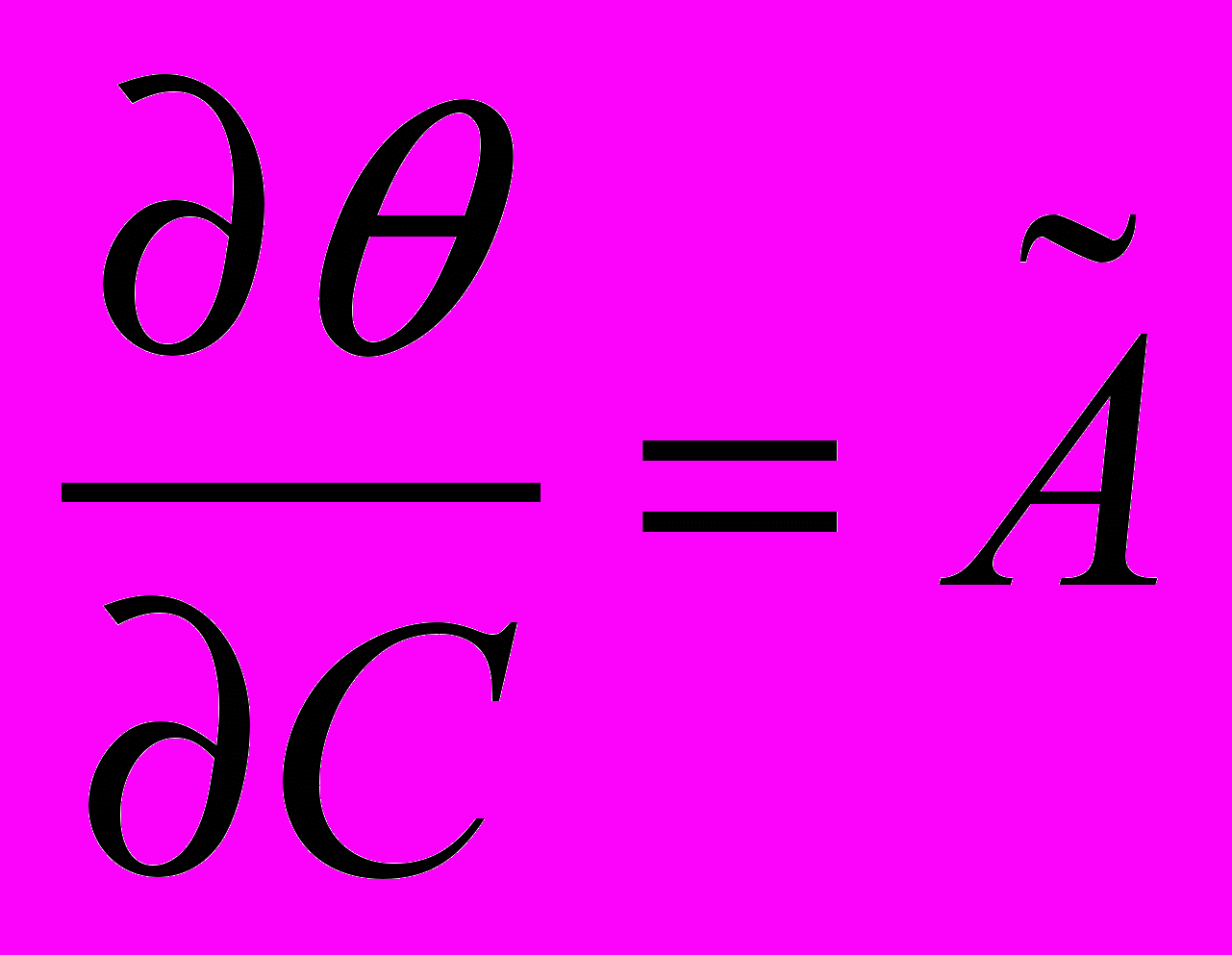 , где
, где 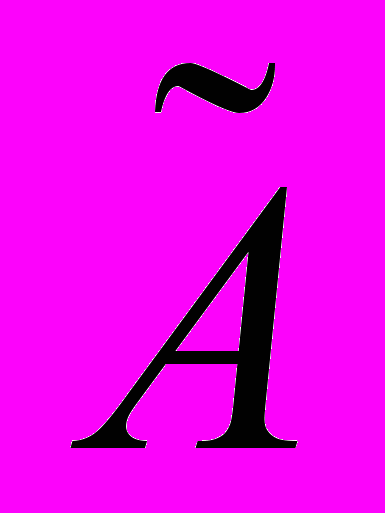 – произвольная постоянная. В результате получится двухпараметрическое уравнение лучей.
– произвольная постоянная. В результате получится двухпараметрическое уравнение лучей.Решение:
Уравнение эйконала
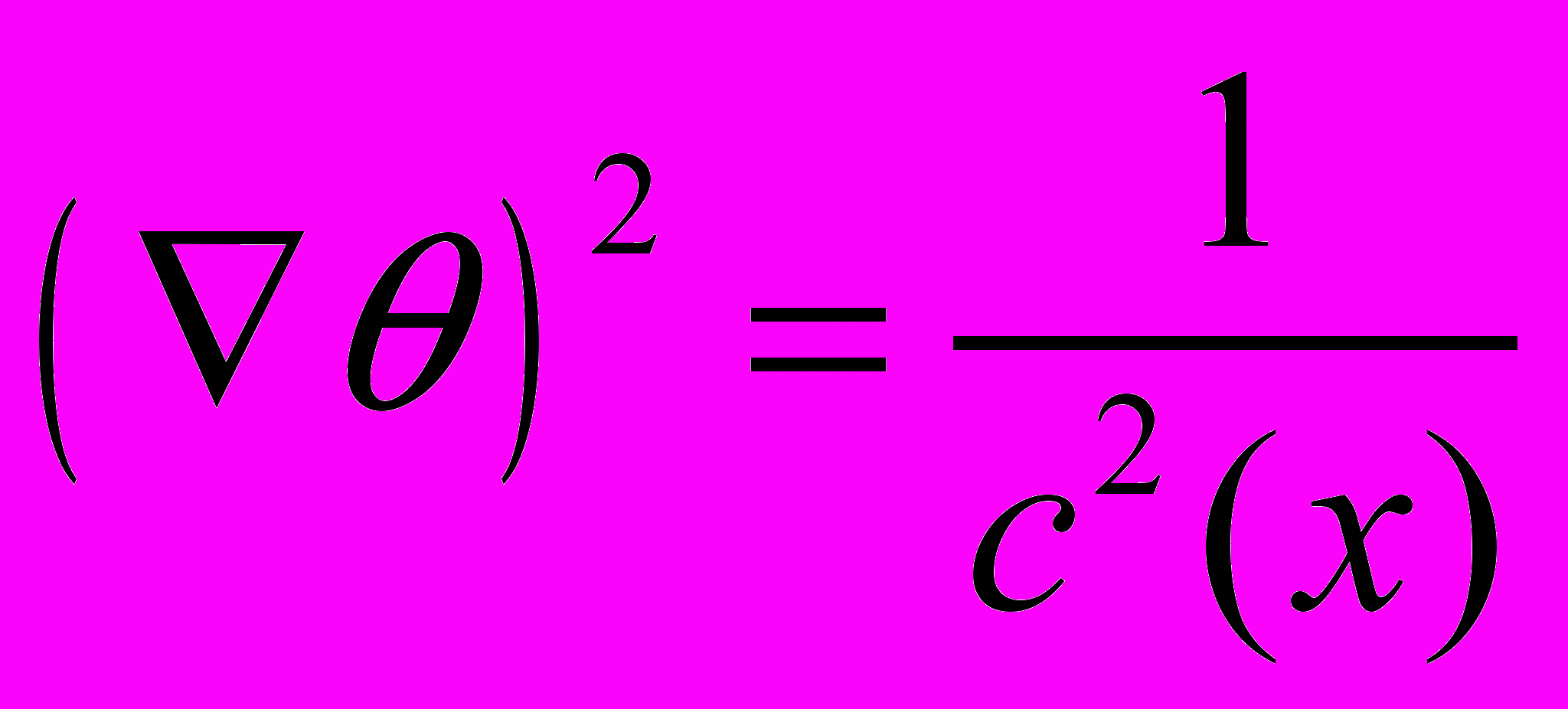 в данном случае имеет вид:
в данном случае имеет вид: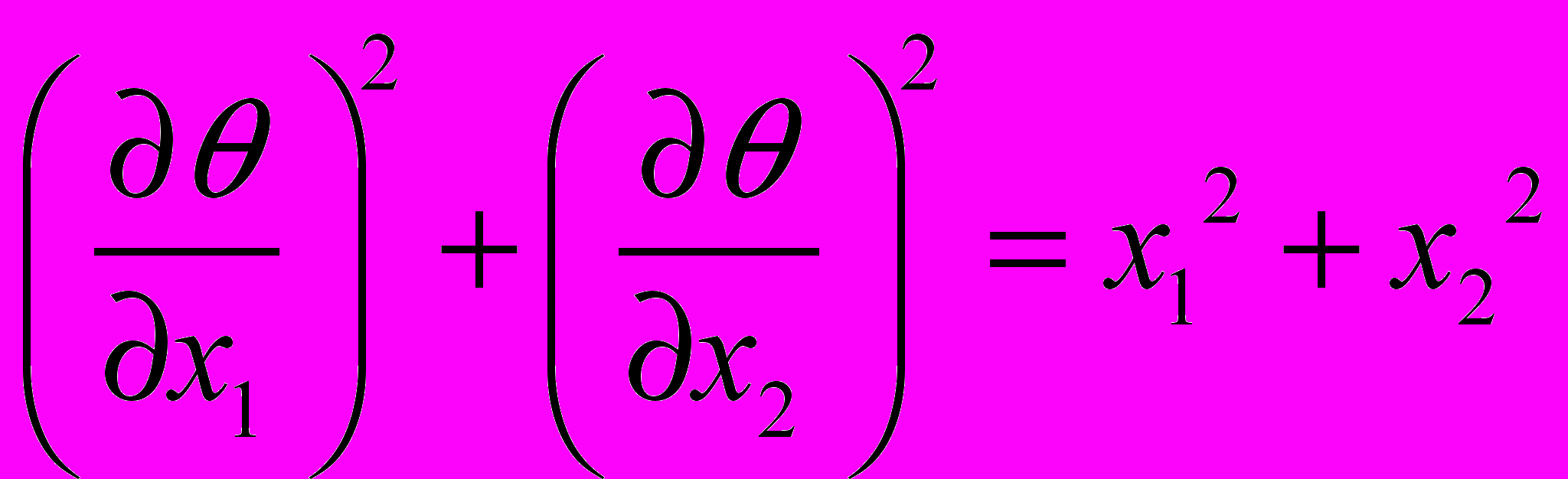 .
.После разделения переменных получим
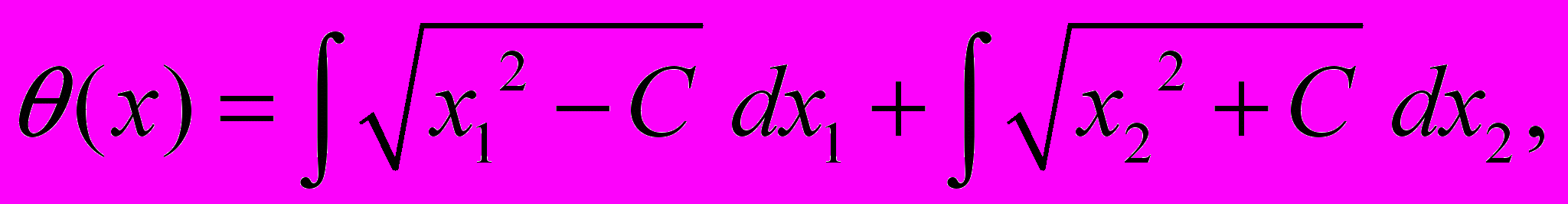
где
 - постоянная разделения переменных. Уравнения лучей находим из соотношения
- постоянная разделения переменных. Уравнения лучей находим из соотношения 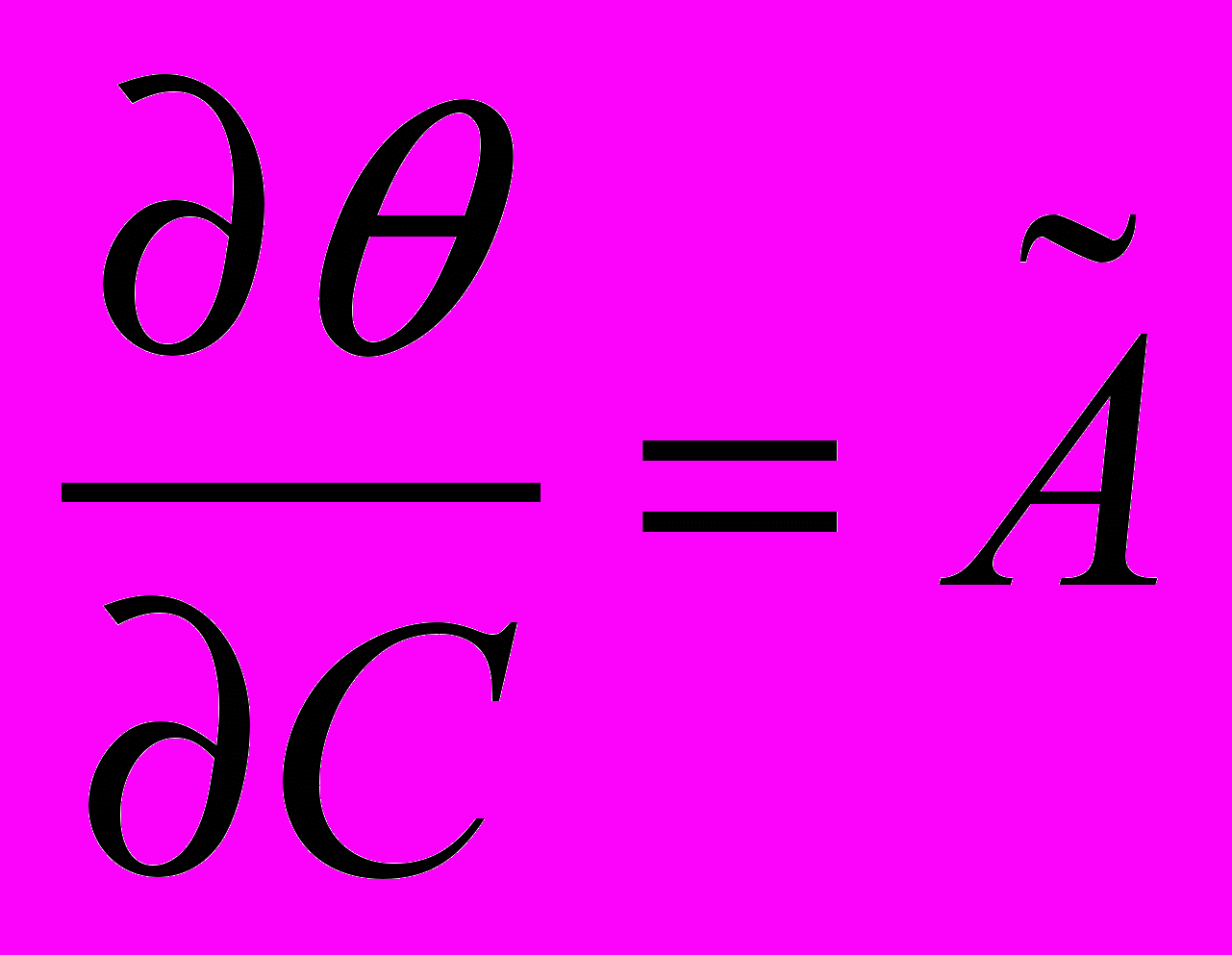 , где
, где 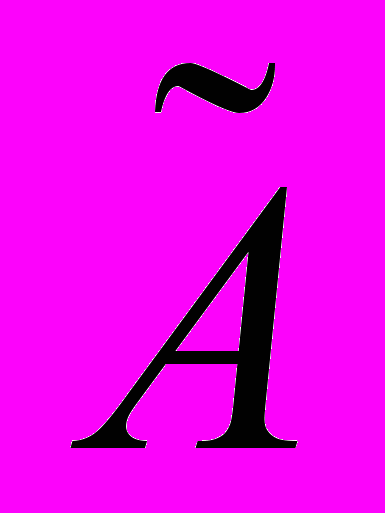 – произвольная постоянная:
– произвольная постоянная: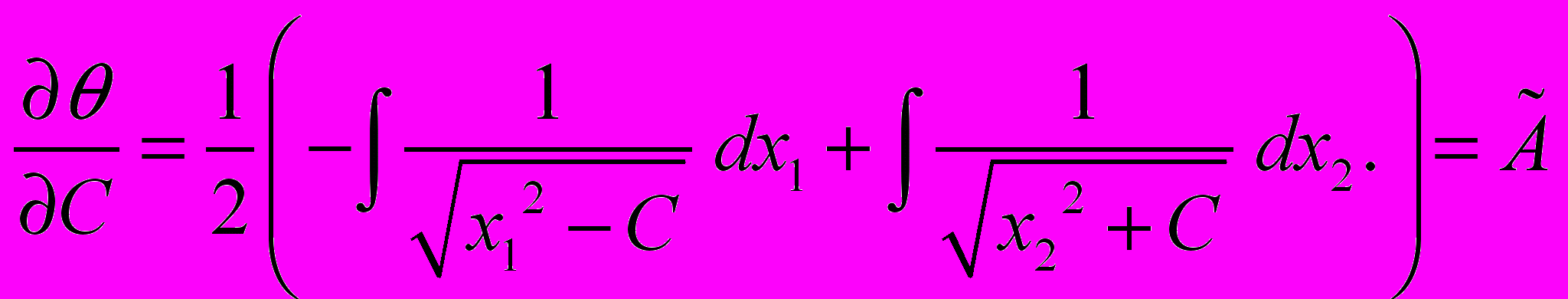
После интегрирования получим
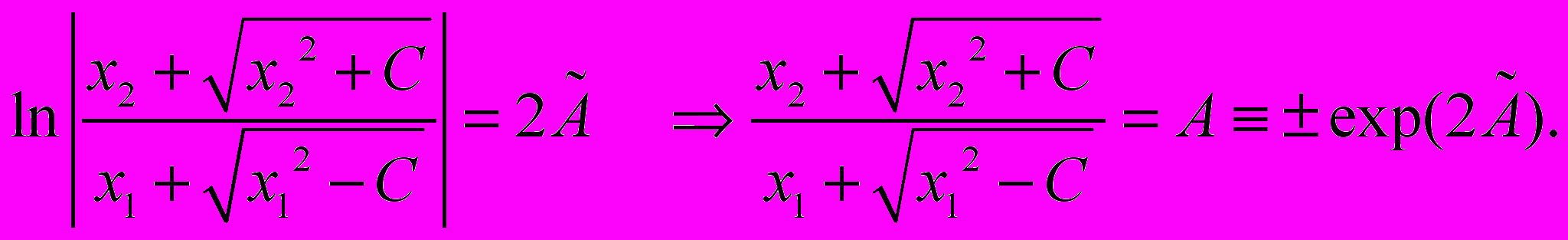
Отсюда окончательно имеем двухпараметрическое семейство гипербол
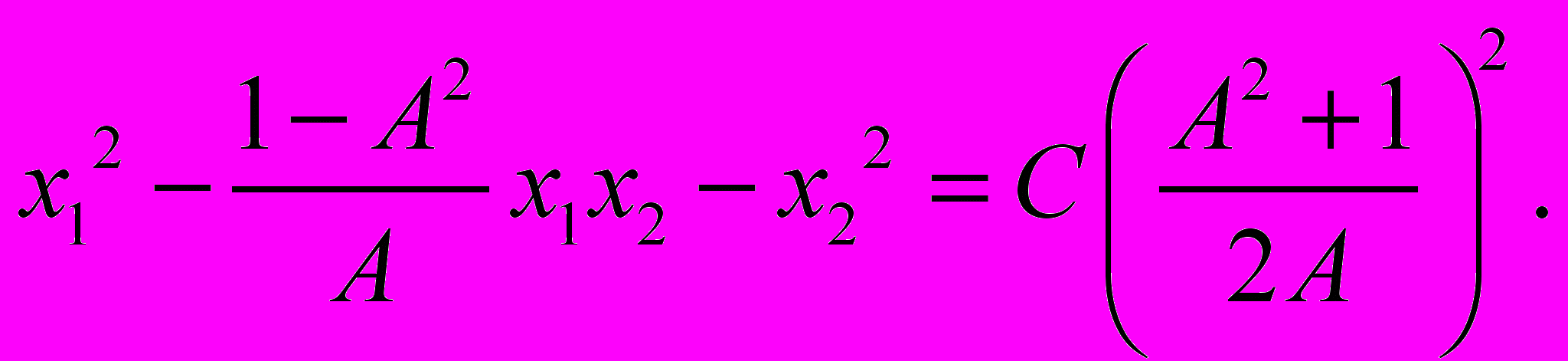
Основы вариационного исчисления можно вспомнить, обратившись к:
Смирнов В.И., Курс высшей математики, том IV, часть первая, М: Наука, 1974
Там же содержатся некоторые вычисления с функционалом Ферма
Литература по теме Высокочастотные асимптотики для уравнения Гельмгольца в неоднородной среде:
Бабич В.М., Булдырев В.С., Асимптотические методы в задачах дифракции коротких волн. Метод эталонных задач, М: Наука, 1972
