Лекция 17. Несобственные интегралы

Вид материала

Лекция

Подобный материал:

• Лекция 22 Несобственные интегралы на неограниченном промежутке, 30.33kb.
• Программа дисциплины «Математический анализ», 500.52kb.
• Программа дисциплины «математический анализ», 432.47kb.
• Программа обсуждена на заседании кафедры Математики фнти, 28.33kb.
• «Социальная стратификация и социальная мобильность», 46.19kb.
• «Неопределенные и определенные интегралы», 13.17kb.
• Программа курса двойные интегралы в пространстве и векторный анализ, 59.08kb.
• Л. Д. Ландау и Е. М. Лифшиц. Механика. М., Hayка, 1988, 82.82kb.
• Программа государственного экзамена по физике Специальность 010400 -физика, 72.86kb.
• Квантование энергии частицы в прямоугольной потенциальной яме и туннельный эффект, 22.29kb.

Лекция 17. Несобственные интегралы.


17.1. Интегралы с бесконечными пределами.


Пусть функция f(x) определена и непрерывна на интервале [a, ). Тогда она непрерывна на любом отрезке [a, b].


Определение: Если существует конечный предел 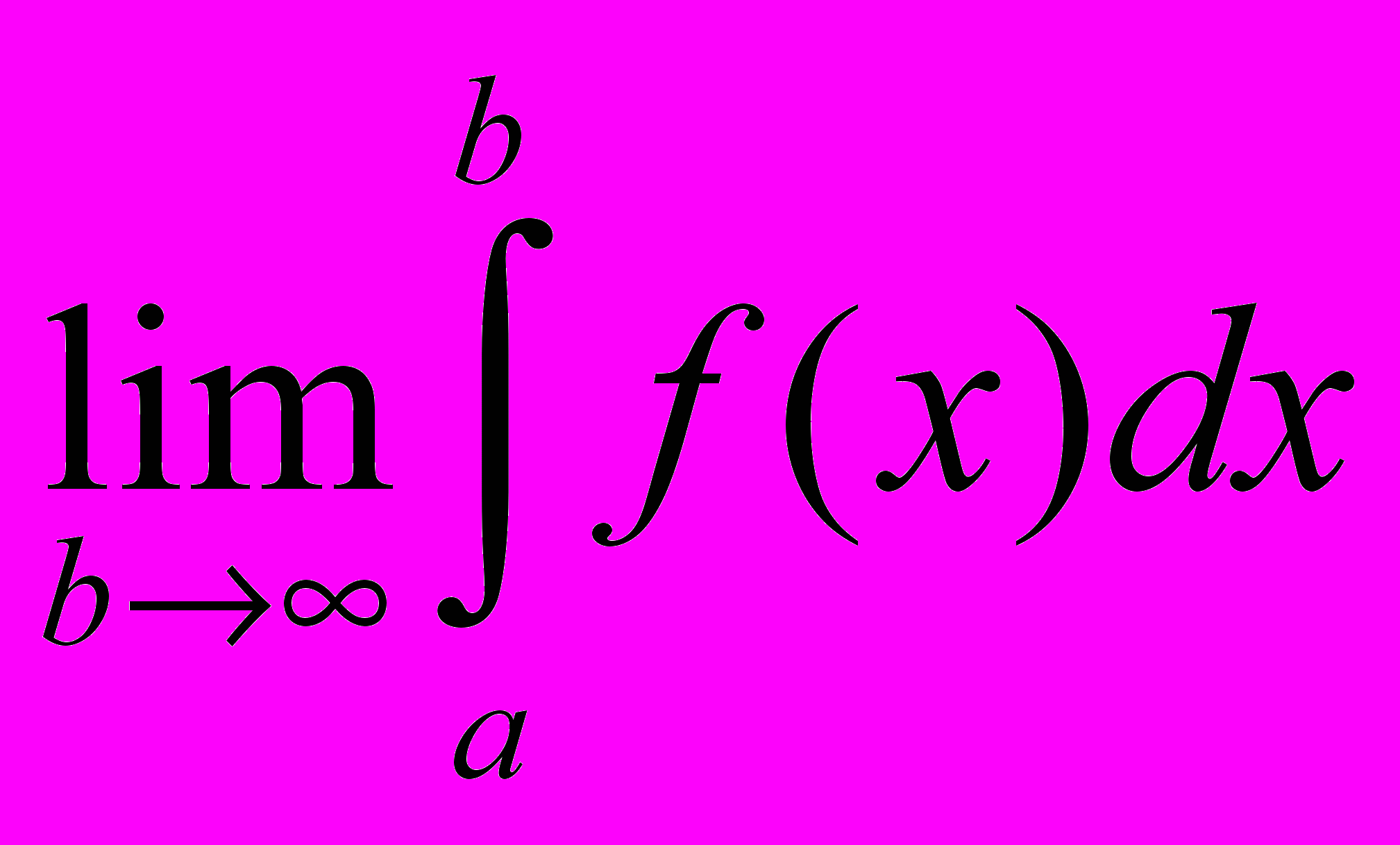, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ).

Обозначение:


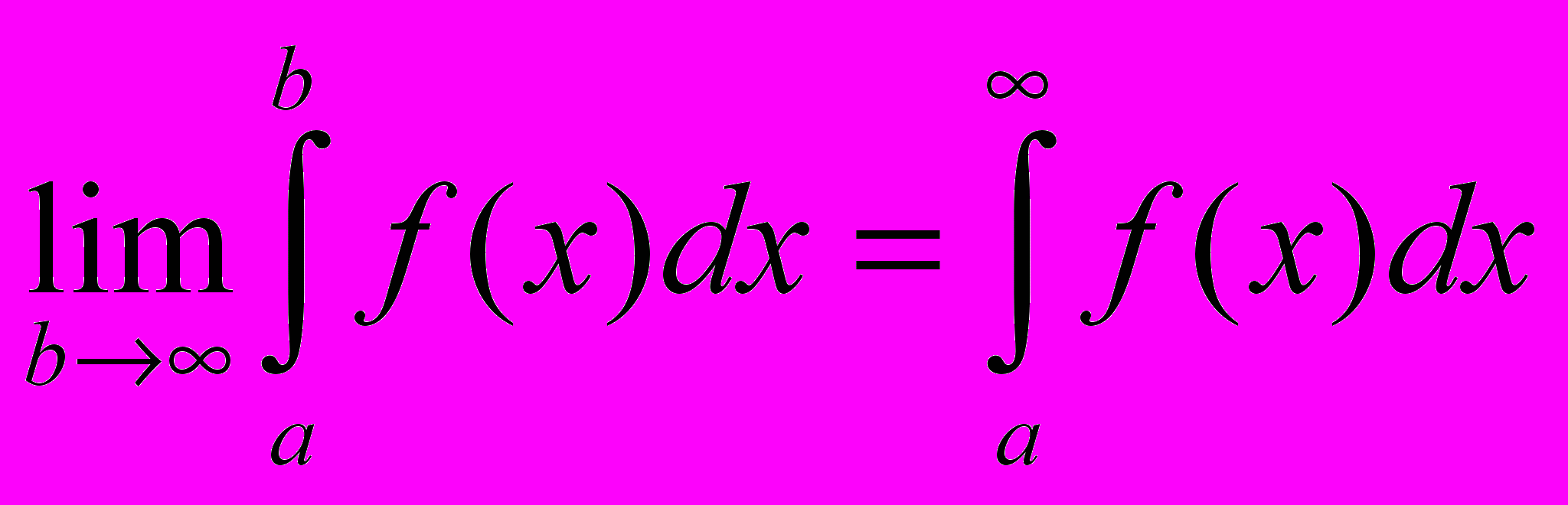
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.


Аналогичные рассуждения можно привести для несобственных интегралов вида:





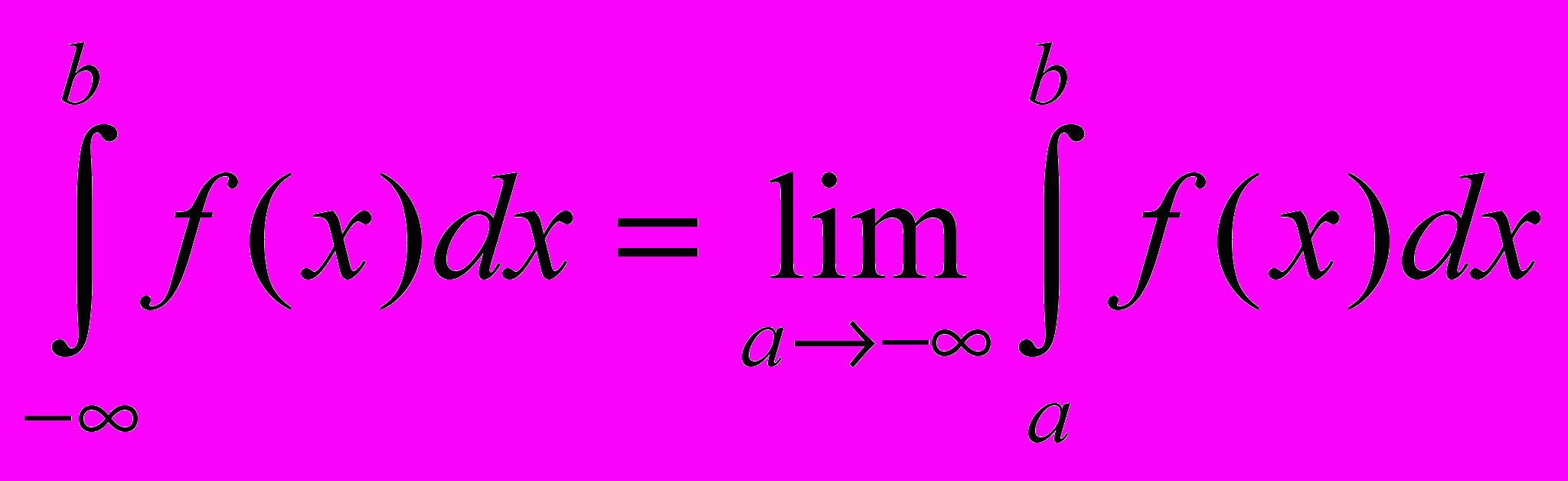
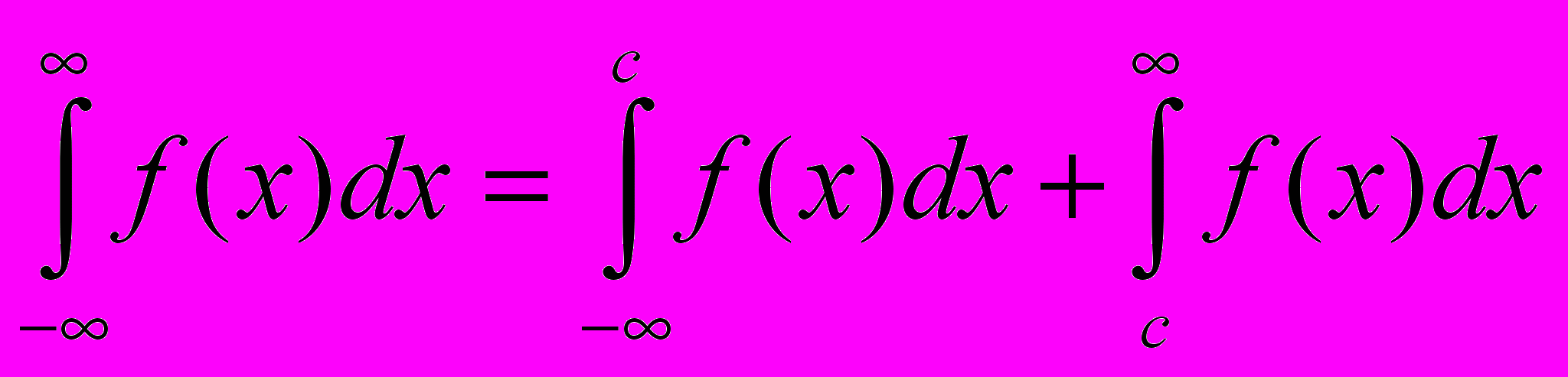
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.


Пример.

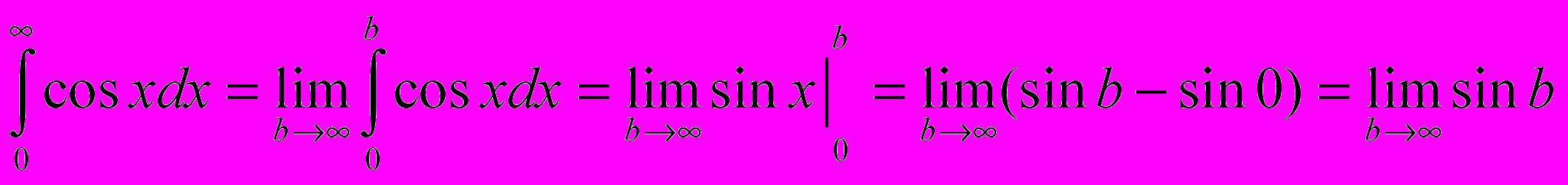- не существует.

Несобственный интеграл расходится.


Пример.


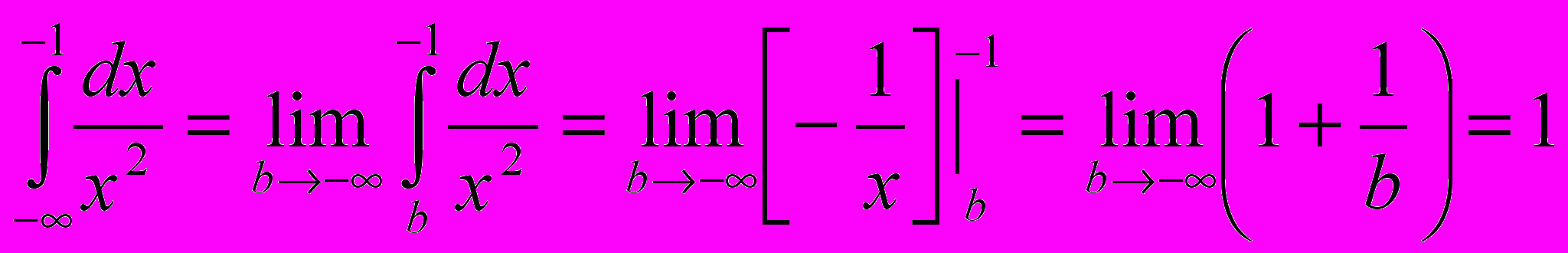- интеграл сходится


Теорема: Если для всех х (x  a) выполняется условие 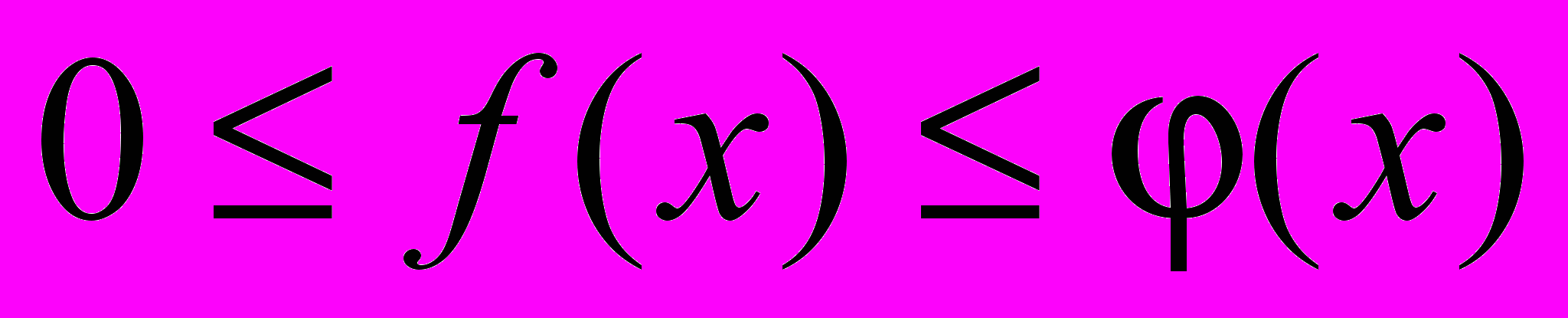и интеграл 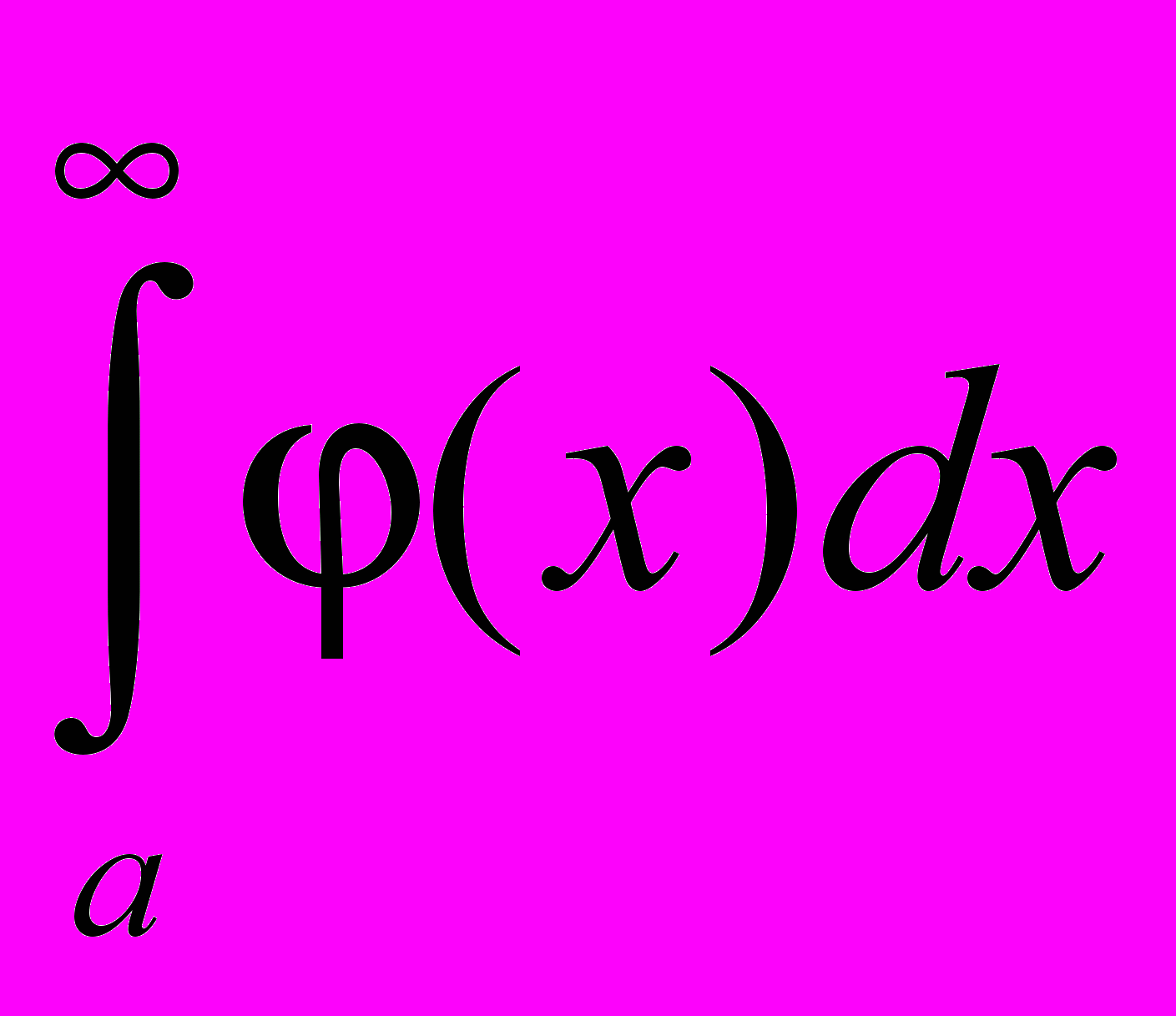сходится, то 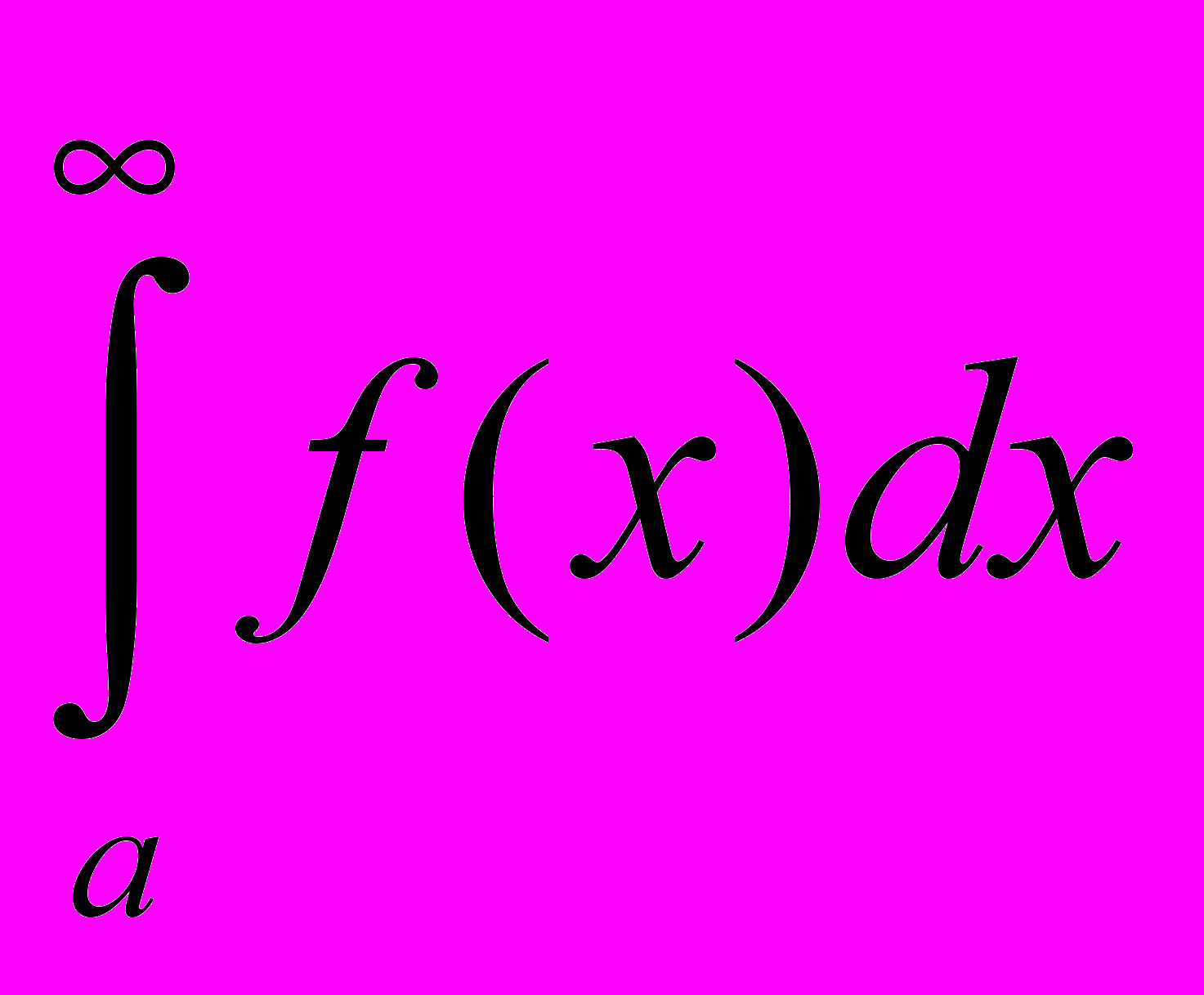тоже сходится и  .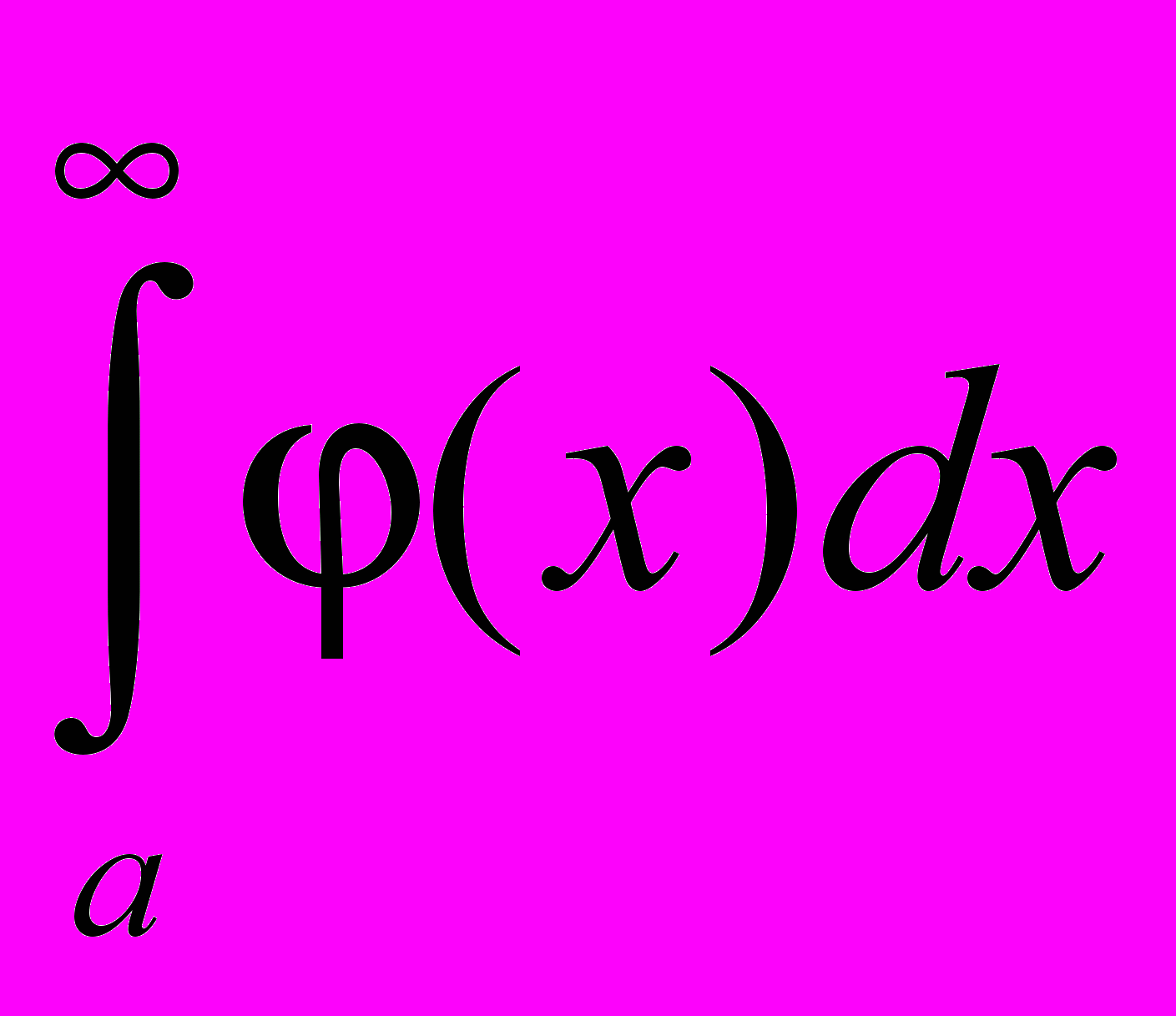


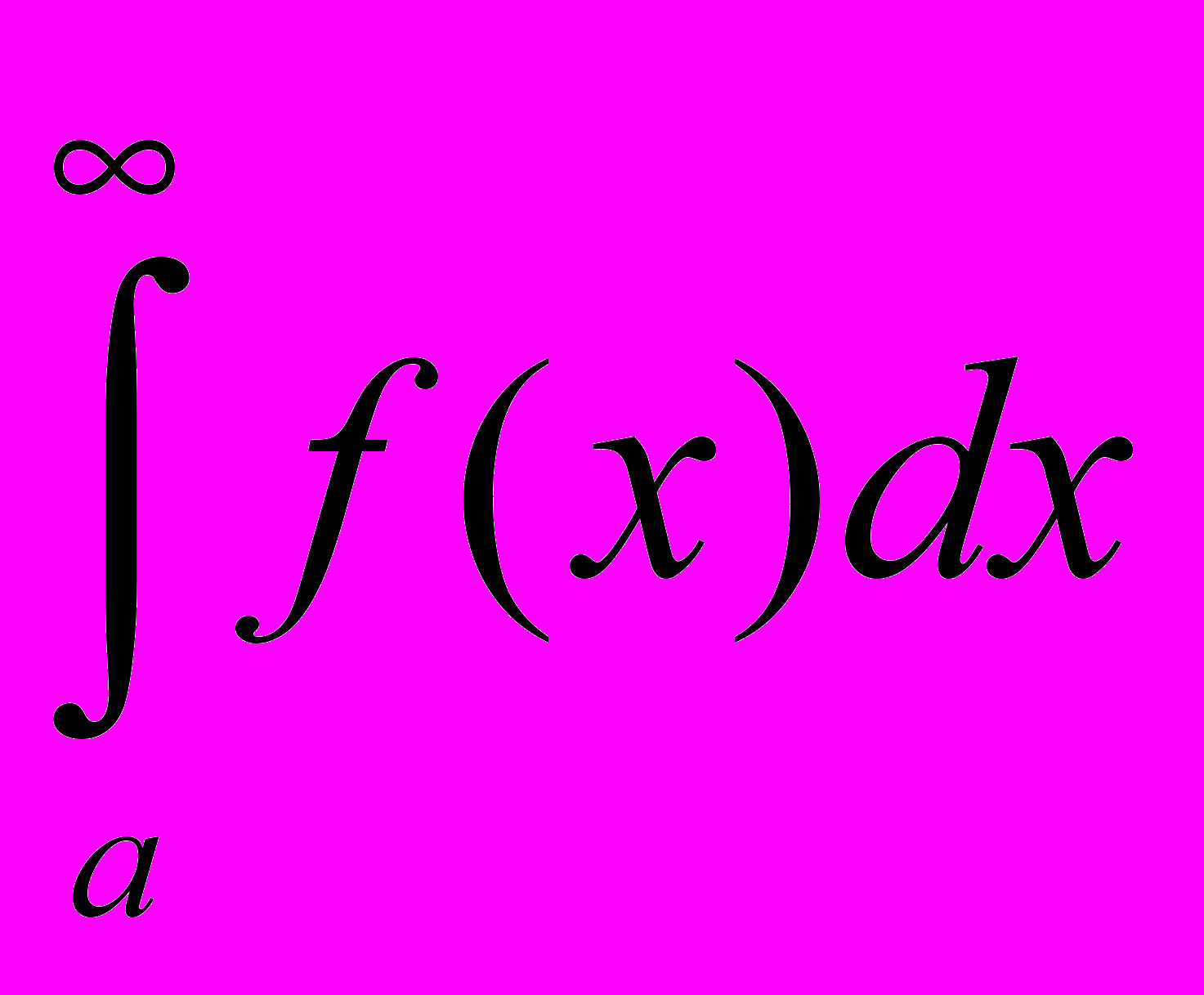Теорема: Если для всех х (x  a) выполняется условие 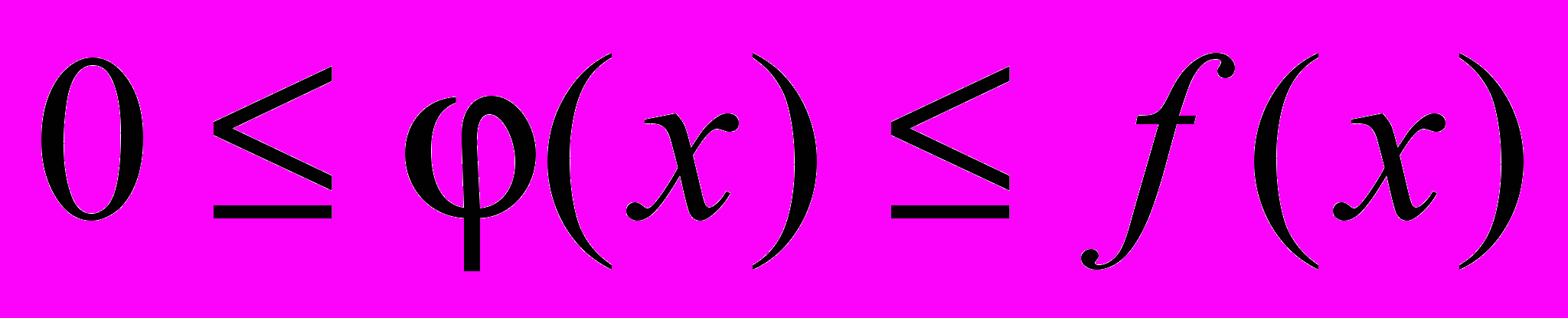и интеграл 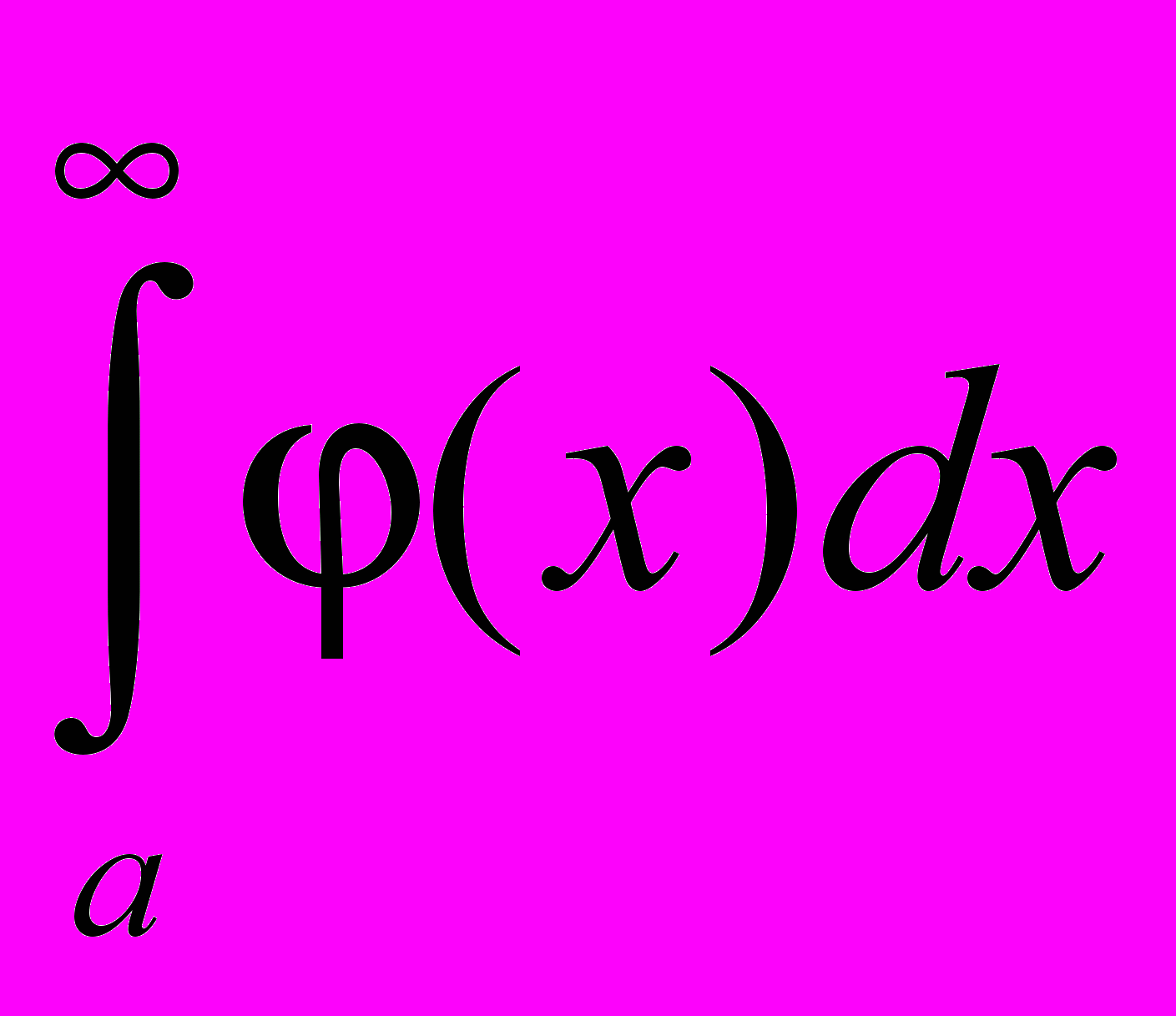расходится, то 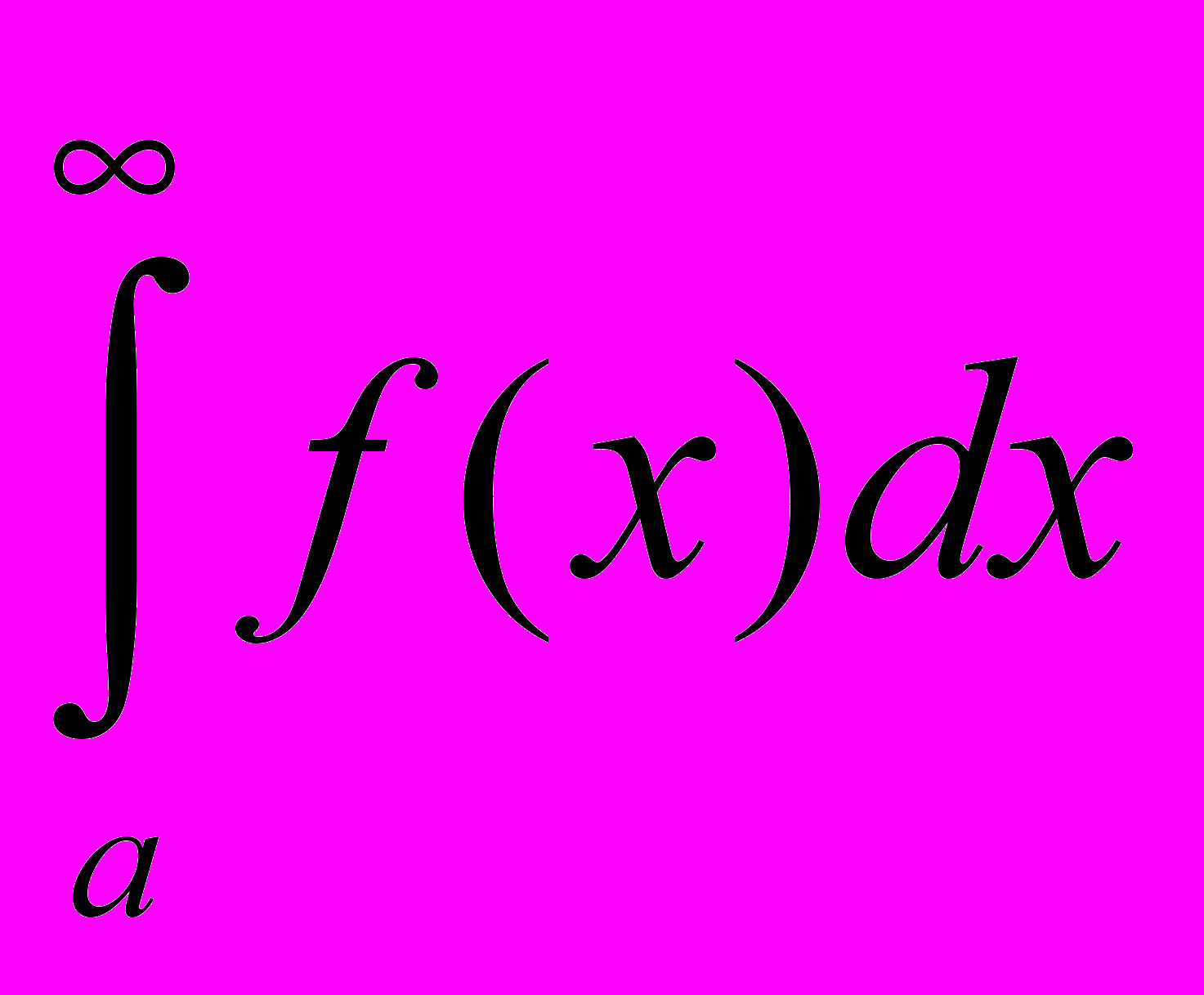тоже расходится.


Теорема: Если 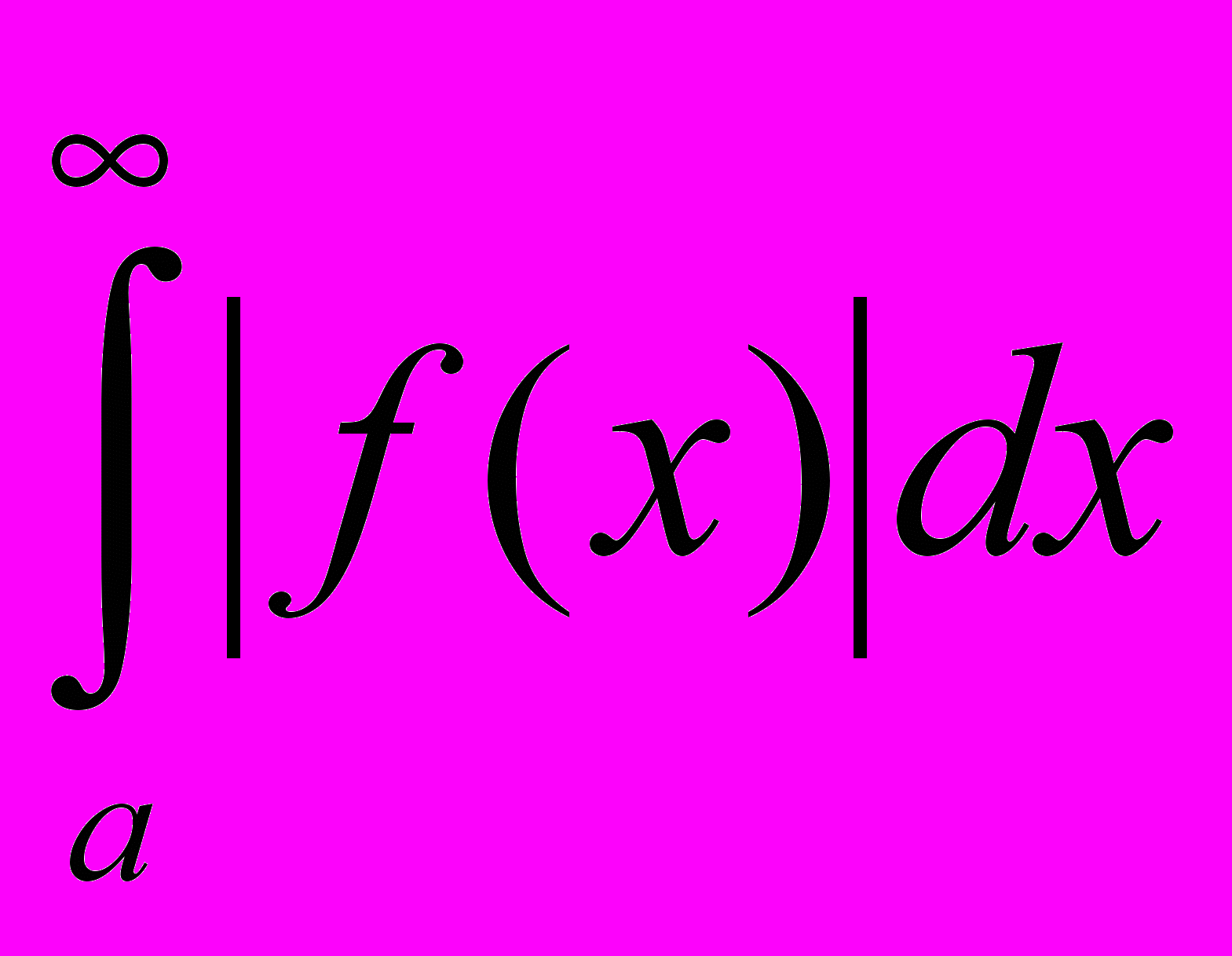сходится, то сходится и интеграл .

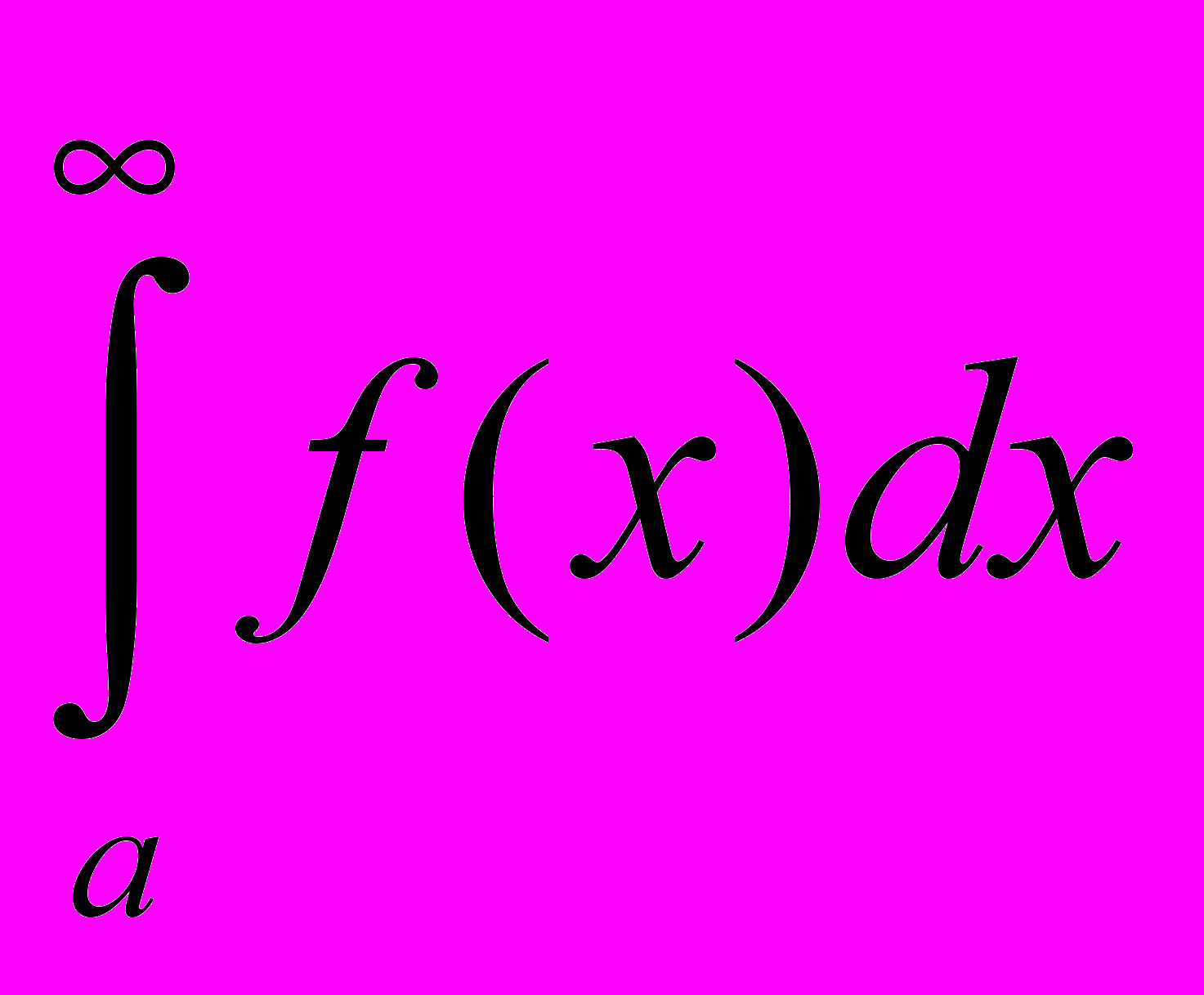В этом случае интеграл 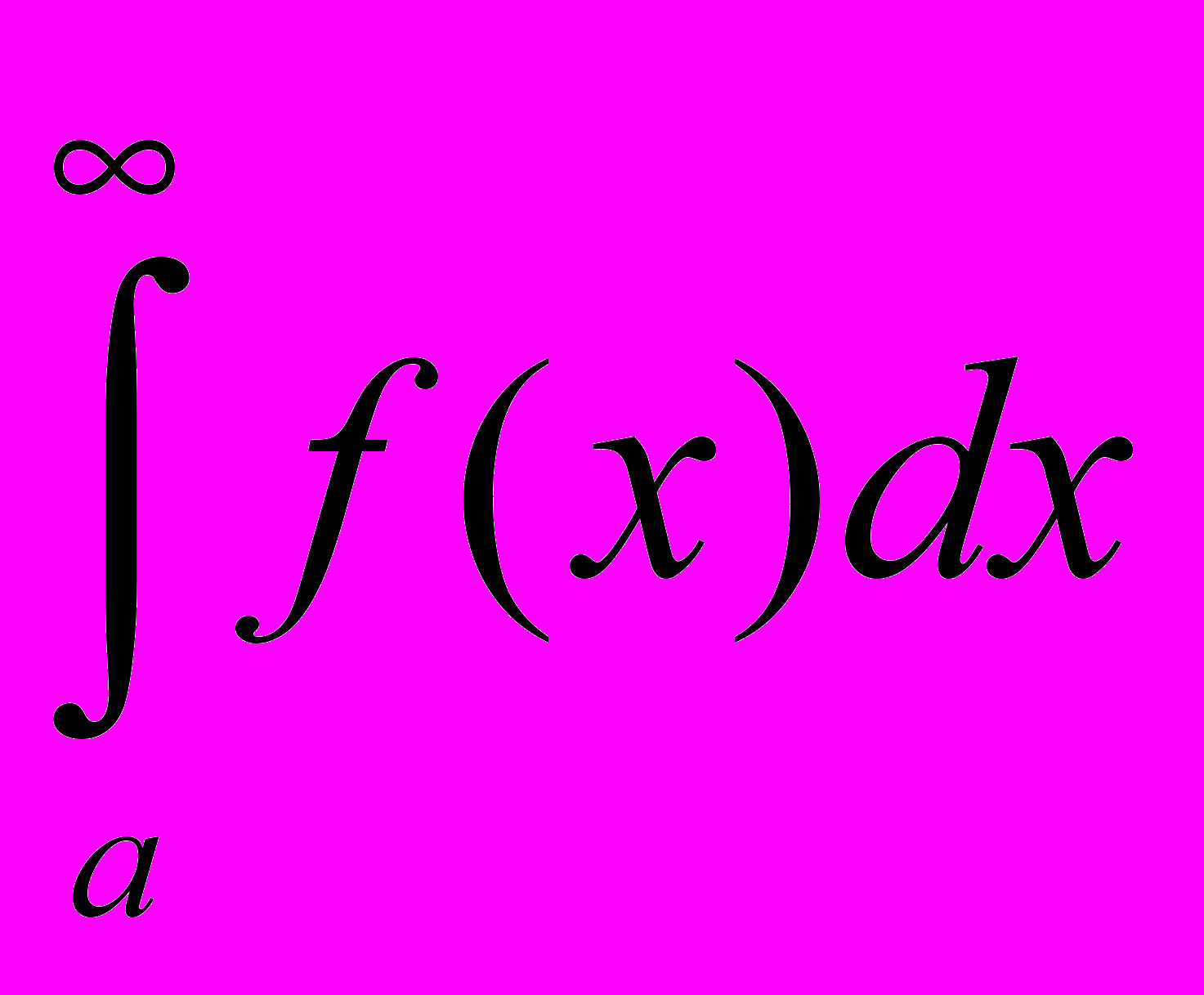называется абсолютно сходящимся.


17.2. Интеграл от разрывной функции.


Если в точке х = с функция либо неопределена, либо разрывна, то



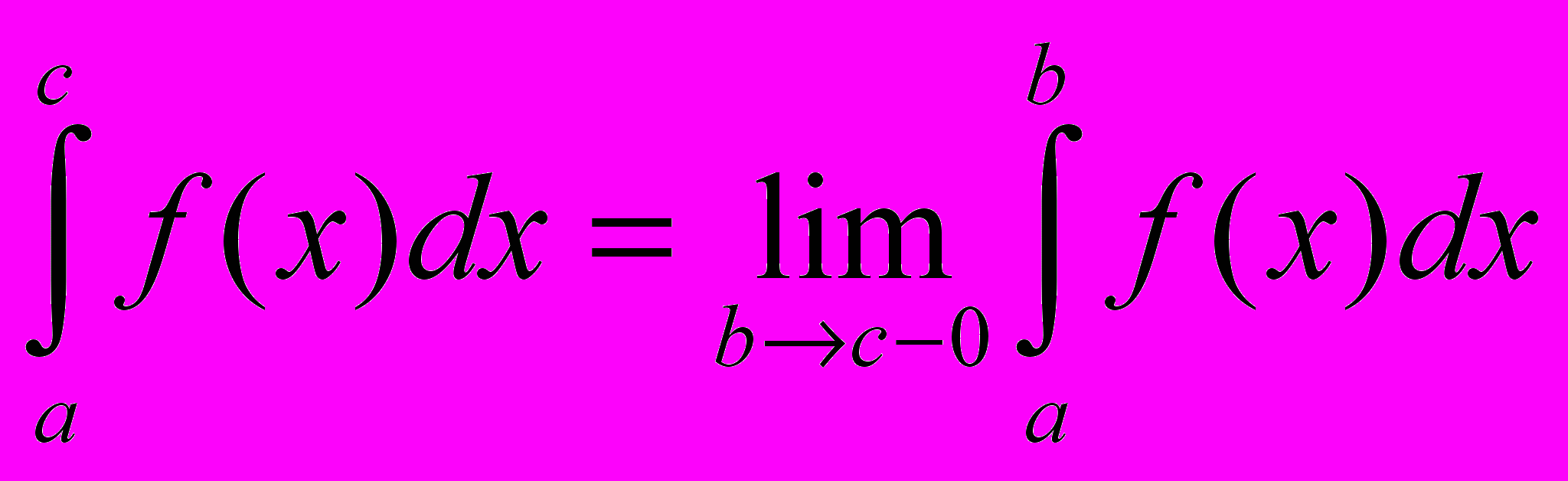
Если интеграл 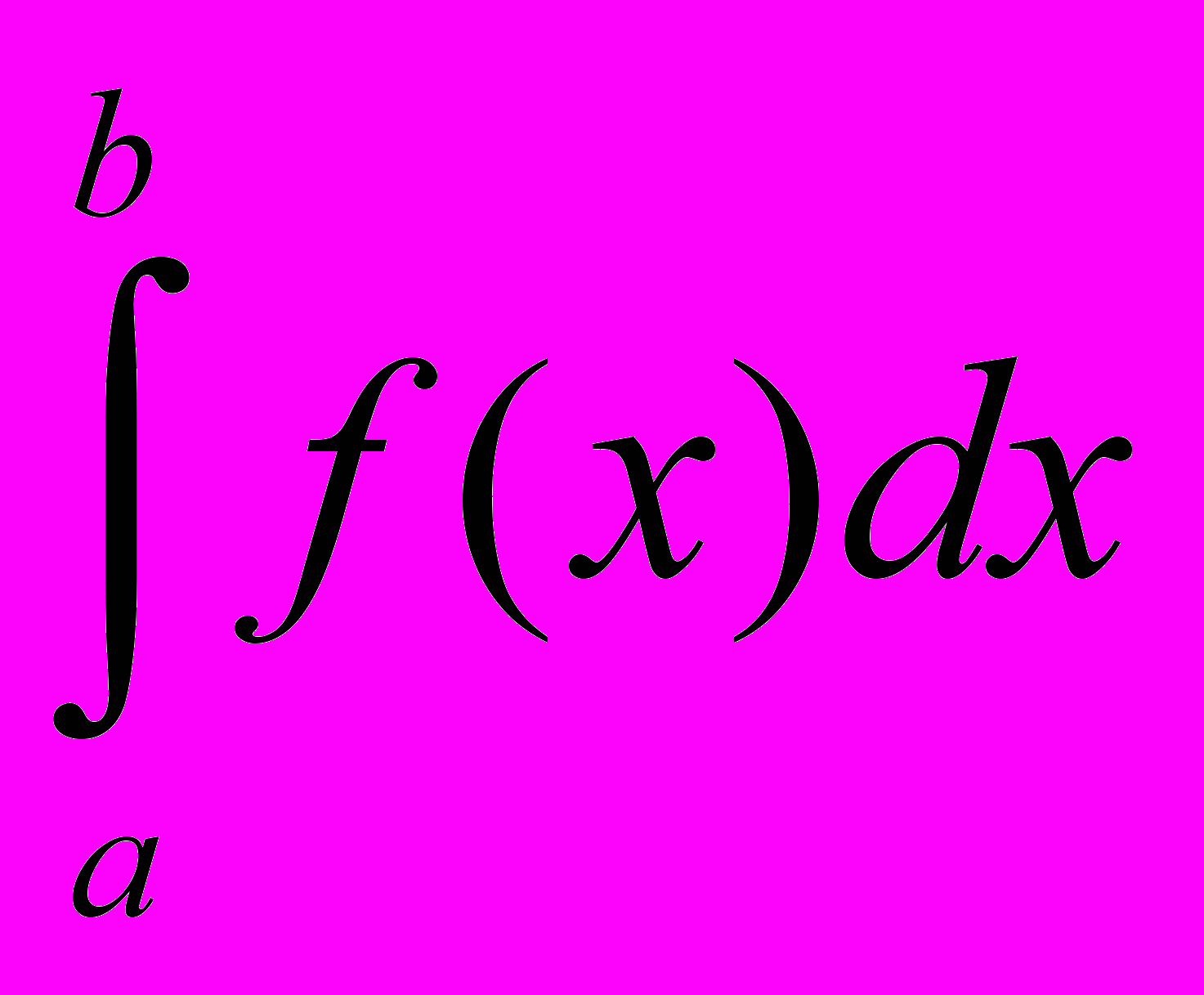существует, то интеграл 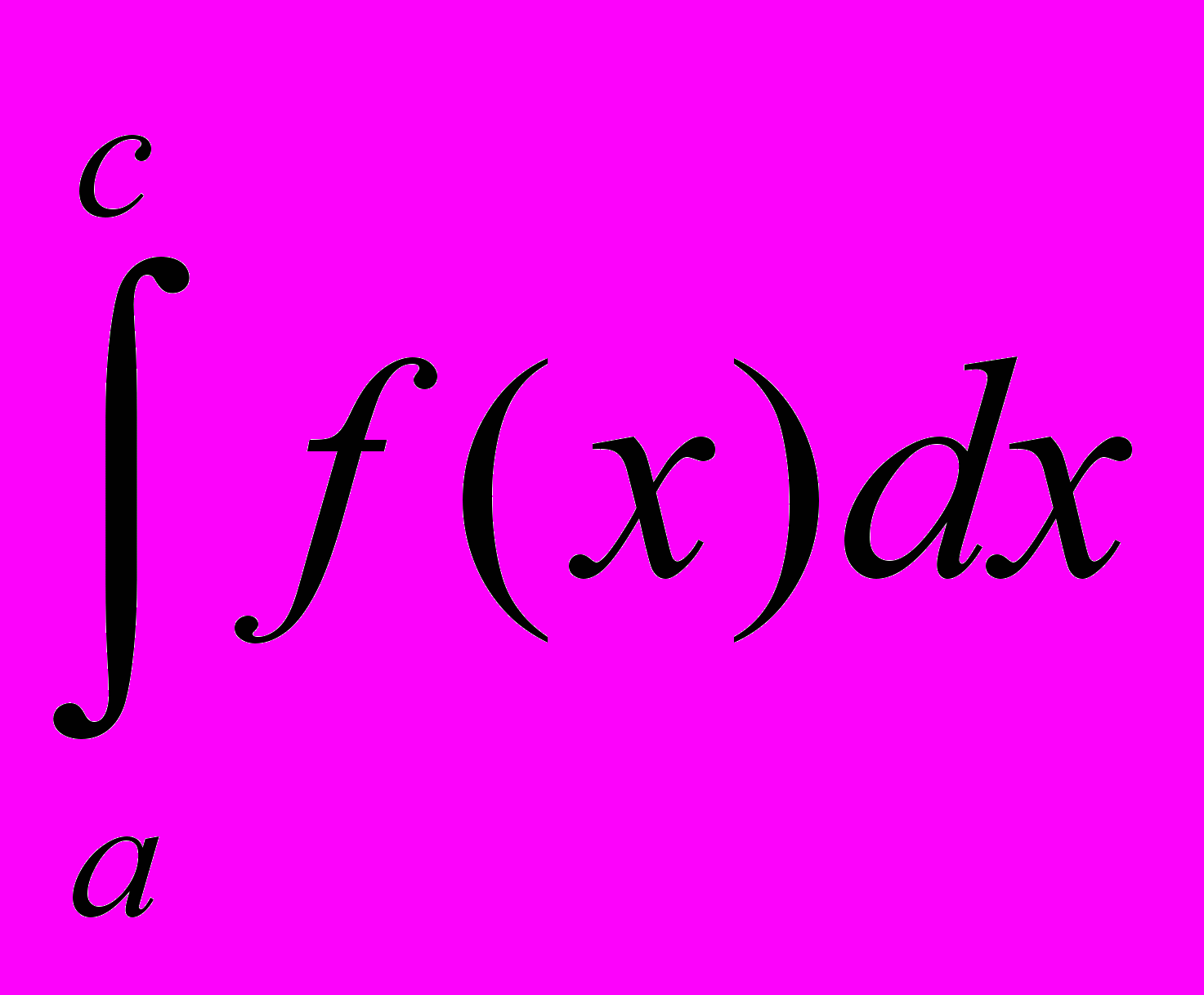- сходится, если интеграл 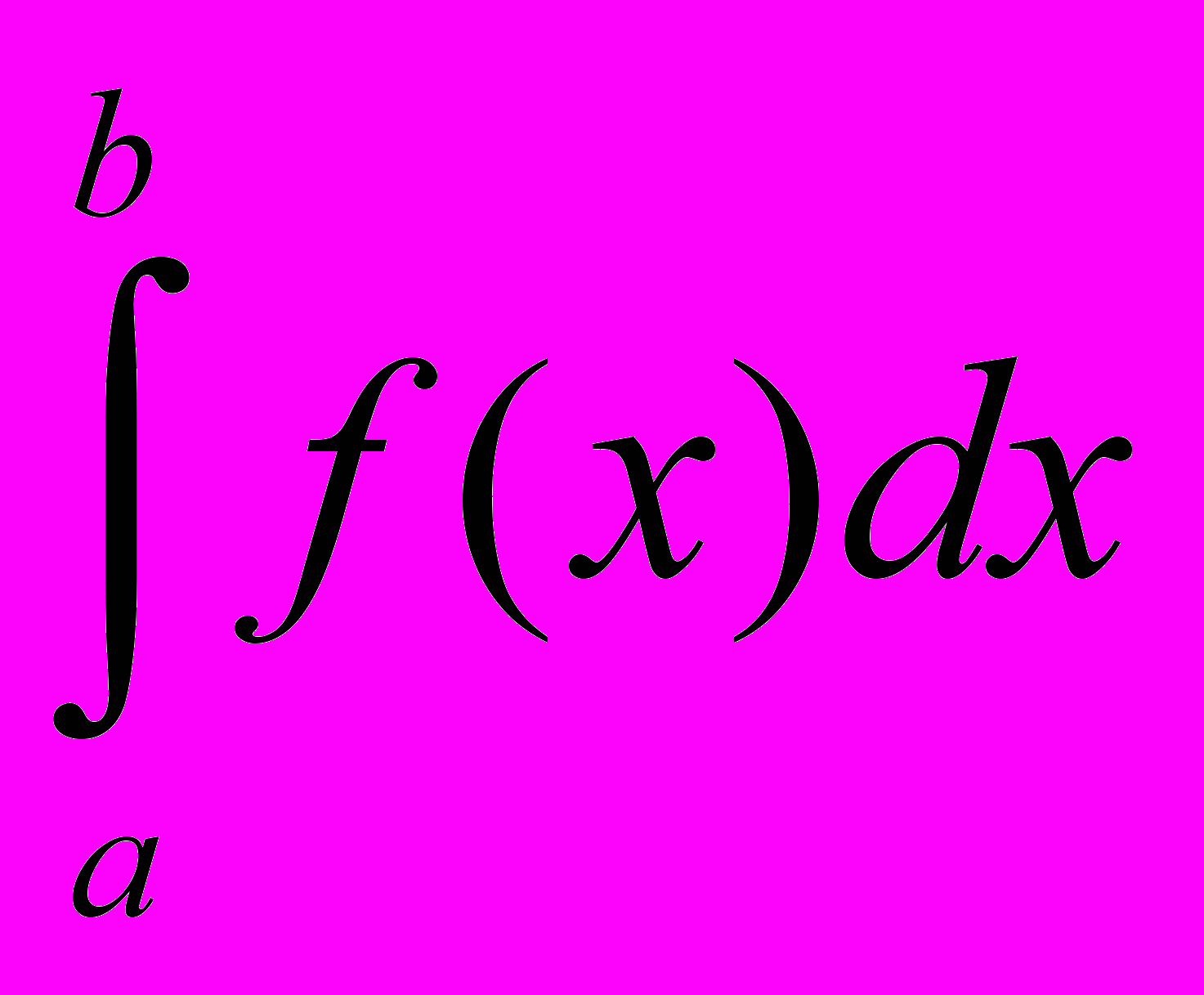не существует, то 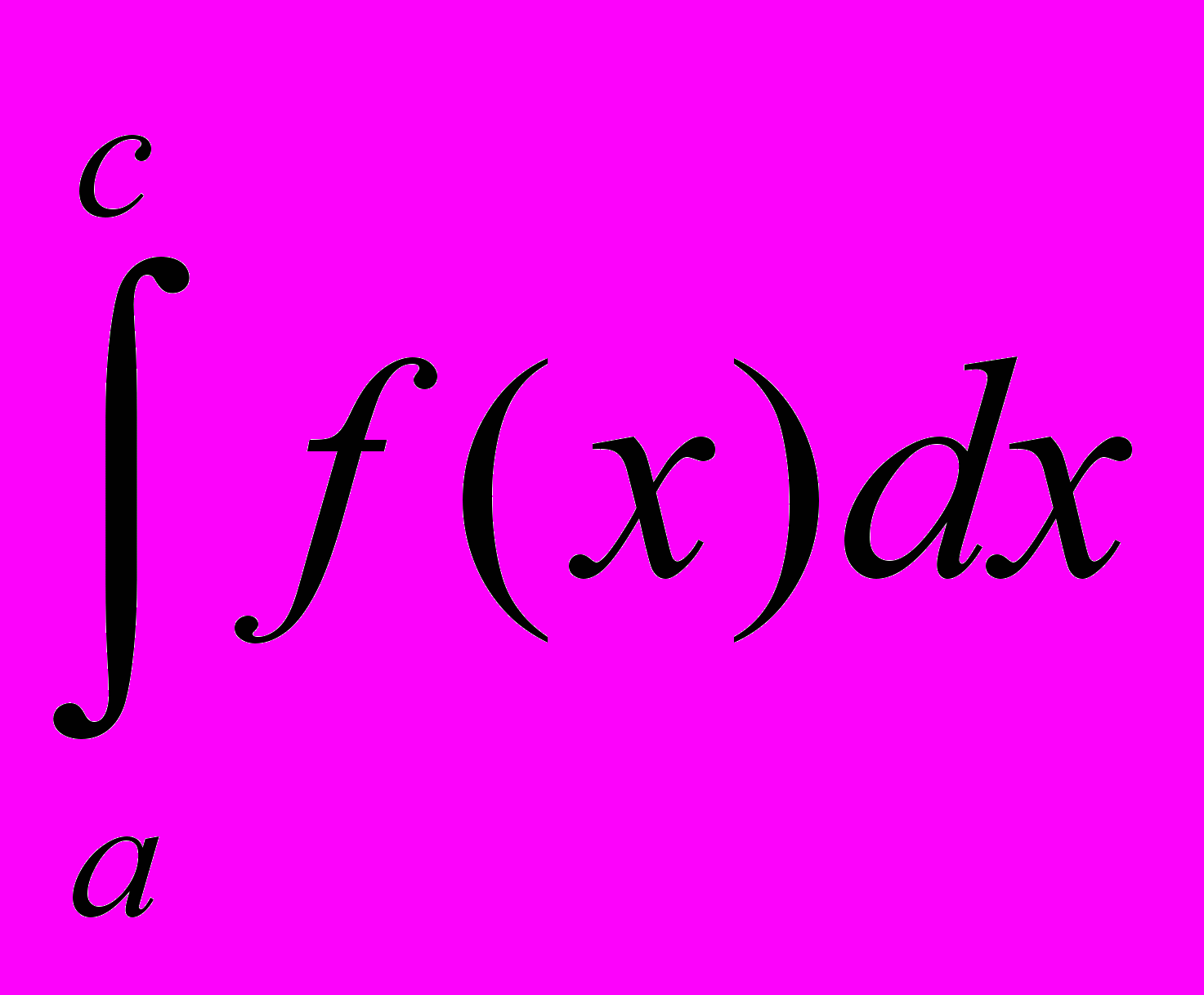- расходится.


Если в точке х = а функция терпит разрыв, то .

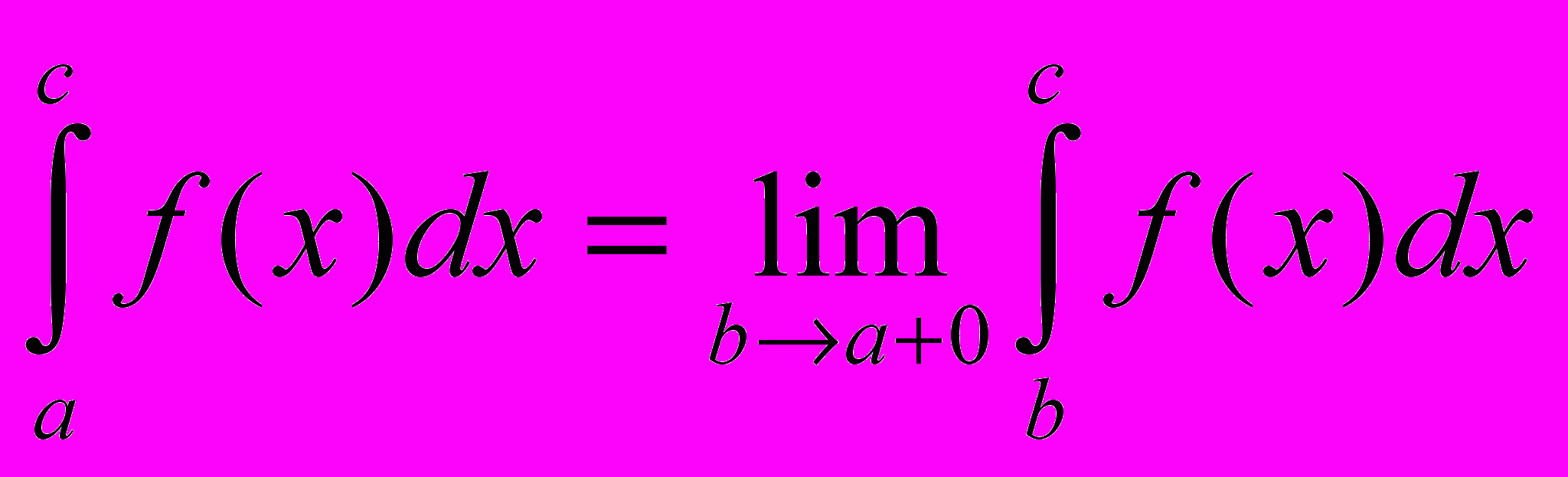Если функция f(x) имеет разрыв в точке b на промежутке [a, с], то



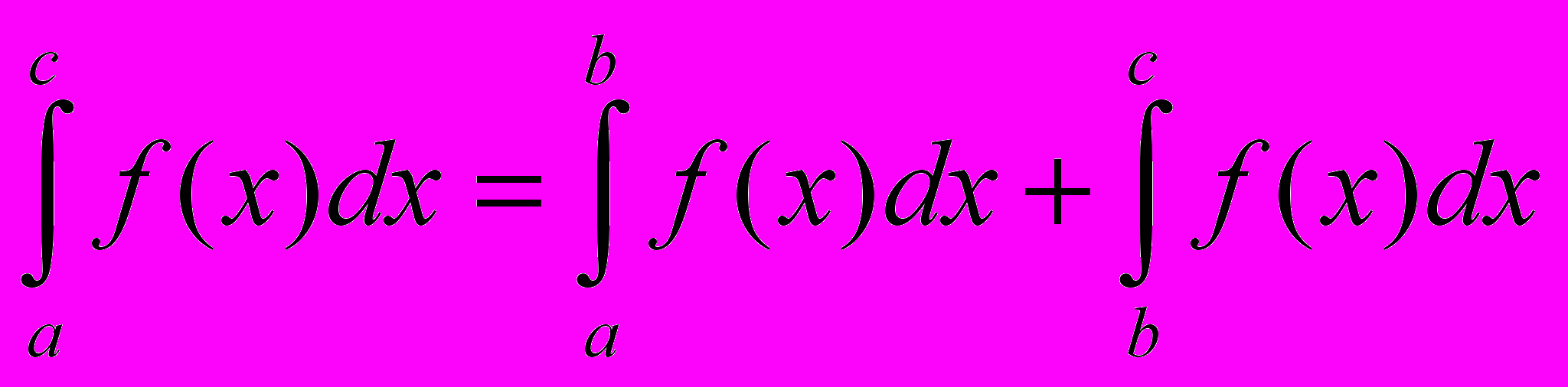
Таких точек внутри отрезка может быть несколько.

Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.