Г в в аудитории 406 (Ленинградский просп., д. 49) состоится очередное заседание
| Вид материала | Заседание |
- Агентство Городского Развития состоится очередное заседание, 18.85kb.
- «Специфика организации мероприятий в розничной торговле на примере сети «Пятерочка», 118.99kb.
- Фото Олега Паршина 23 ноября 2011 года в Доме русского зарубежья состоялось очередное, 44.14kb.
- Моделирование конкуренции на рынке информационных технологий, 30.72kb.
- Совета Безопасности Республики Татарстан от 17. 08. 2007 №30 о мерах по противодействию, 78.84kb.
- 14 октября Заседание регионального отделения Общественного совета, 13.86kb.
- 8 июля в Киеве прошло очередное заседание Центра социально-консервативной политики, 42.54kb.
- Электронная газета русской диаспоры в Швеции, 225.26kb.
- Коваленко Елены Игоревны. Разное научная часть 22 октября 2007 года в 14. 00 час, 18.73kb.
- Аналитическая записка о состоянии и проблемах законотворчества, 257.67kb.
22 марта 2011 г. в
в аудитории 406 (Ленинградский просп., д.49) состоится очередное заседание научного семинара кафедры «Математика» «Современная математика и концепции инновационного математического образования»
под руководством проф. С.Е. Степанова
Докладчик:
Юрген Аппель (Университет Вюрцбург, ФРГ)
Тема: «Теория и приложения уплотняющих операторов: старое и новое»
Аннотация.
Теория уплотняющих операторов тесно связана с понятием меры некомпактности. Хотя первая конкретная мера некомпактности была введена К. Куратовским еще в 1930 году, в основном теория мер некомпактности и уплотняющих операторов была построена за последние 50 лет. Оказалось, что уплотняющие операторы во многом похожи на компактные. В частности, для отображений вида
, где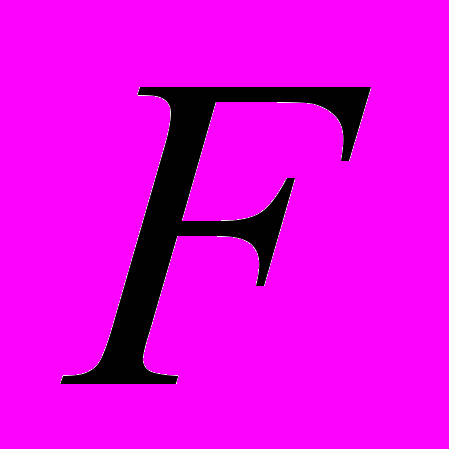 
– уплотняющий (линейный или нелинейный) оператор, можно корректно определить топологическую степень, доказать разные теоремы о неподвижных точках или построить теорию Фредгольма-Рисса-Шаудера.Настоящий доклад по замыслу должен служить двум целям: во-первых, дать, возможно, более простое и краткое описание идейной стороны теории таких операторов, и, во-вторых, продемонстрировать некоторые типичные (в том числе, новые) примеры и приложения теории к нелинейным проблемам, в которых естественным образом возникают некомпактные уплотняющие операторы. Подчеркнем, что изложение результатов и примеров будет совсем элементарным и не требующим глубоких знаний по нелинейному анализу.