Geum.ru

Возможность использования искусственных спутников Земли для обнаружения гравитационных волн

Вид материалаРешение
Подобный материал:
Возможность использования искусственных спутников Земли для обнаружения гравитационных волн.


Н.Т. Сайнюк


Существования квантовых эффектов в гравитации является одним из следствий гипотезы о полевом строении элементарных частиц (mtokma.narod.ru). В работе (mtokma.narod.ru›solar.doc) был проведен квантово механический расчет элементов орбит планет Солнечной системы, который показала, что энергия планет солнечной на орбите их движения является величиной квантовой также как и энергия электронов в атомах. Поэтому можно надеяться, что при движении искусственных спутников в гравитационном поле Земли эти квантовые эффекты также могут проявить себя.

Рассмотрим движение искусственного спутника в гравитационном поле Земли с точки зрения квантовой механики.

Уравнение Шредингера для движения сферического искусственного спутника в гравитационном поле Земли по круговой орбите можно представить в виде:

(1);


где m - масса спутника;

M - масса Земли;

G - гравитационная константа.


Решение уравнения (1) будет:

(2)


Где

Энергию можно пересчитать в квантовые радиусы орбит спутника:

(3);

Учитывая, что для спутника, движущегося в гравитационном поле Земли, значение постоянной Планка определяется выражением:


(4)

где - масса спутника

- диаметр этого спутника

- скорость света

Тогда выражение (3) примет вид:

(5)

Где - радиус спутника

Для спутника радиусом 1м значения квантовых чисел 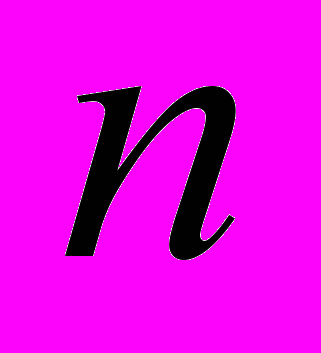, радиусов квантовых орбит, высота орбит над уровнем моря , а также расстояние между двумя соседними орбитами , рассчитанными по формуле (5) представлены в таблице 1.


Таблица 1.

Значение квантового числа,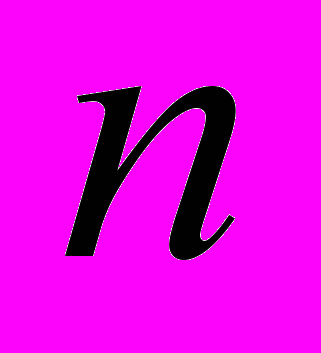

Радиус круговой орбиты спутника , Км
Высота орбиты над уровнем моря , Км
Разница по высоте между соседними орбитами , Км

…
…
…
…

530
6432,61
61,31
 

531
6456,88
85,58
24,27

532
6481,24
109,94
24,36

533
6505,64
134,34
24,4

534
6530,07
158,77
24,43

535
6554,55
183,25
24,48

536
6579,08
207,78
24,53

537
6603,65
232,35
24,57

538
6628,27
256,97
24,62

539
6652,93
281,63
24,66

540
6677,64
306,34
24,71

541
6702,39
331,09
24,75

542
6727,2
355,9
24,81

543
6752,04
380,74
24,84

544
6776,93
405,63
24,89

545
6801,87
430,57
24,94

546
6826,86
455,56
24,99

547
6851,89
480,59
25,03

548
6876,96
505,66
25,07

549
6902,08
530,78
25,12

550
6927,25
555,95
25,17

551
6952,46
581,16
25,21

552
6977,72
606,42
25,26

553
7003,03
631,73
25,31

554
7028,38
657,08
25,35

555
7053,77
682,47
25,39

556
7079,21
707,91
25,44

557
7104,7
733,4
25,49

558
7130,24
758,94
25,54

559
7155,82
784,52
25,58

560
7181,44
810,14
25,62

…
…
…
…


Если гравитационные волны существуют, то при снижении спутника с одной квантовой орбиты на другую можно ожидать, что часть его энергии будет расходована на гравитационное излучение. В идеальном случае энергия гравитационной волны равнялась бы разнице в энергиях между соседними квантовыми уровнями, рассчитанными по формуле (2). Но в реальности большую часть энергии на орбите спутник теряет в результате действия других факторов – трения в верхних слоях атмосферы, существования неоднородностей в атмосфере, активности солнца, давления света и т.п. Точно учесть все эти факторы, чтобы определить, какая часть энергии была расходована на гравитационное излучение, вряд ли удастся. Но если гравитационные волны существуют, и спутник их излучает, то это должно приводить к проявлению другого эффекта – замедления скорости потери высоты спутника при его нахождении на квантовых орбитах. Этот эффект легче заметить даже если он существует на уровне помех. Как видно из таблицы, разница между радиусами соседних квантовых орбит при больших значениях квантового числа очень слабо меняется с высотой орбит. Поэтому замедление скорости потери высоты будет почти периодически повторяться при пересечении спутником квантовых орбит на пассивном участке полета (когда двигатели коррекции орбиты и стабилизации спутника в пространстве не включены). В точках пересечения орбиты спутника с квантовыми орбитами первая производная по времени от высоты должна иметь минимумы.

Возможно, этот эффект можно обнаружить обработав уже имеющиеся данные наблюдений за параметрами орбит существующих искусственных спутников Земли или даже тех спутников, которые уже прекратили свое существование, но данные измерений их орбит сохранились. Но при этом необходимо иметь в виду, что большая часть спутников запущенных на низкие орбиты движутся по эллипсу. На значение главного квантового числа это не влияет, но может проявиться при пространственном квантовании орбит из-за влияния на движение спутника Луны и Солнца. Для учета этого эффекта необходимо использовать дополнительно другое квантовое число . Хотя квантовое число ответственно за тонкую структуру спектра и в первом приближении его можно и не учитывать. Кроме того, как это видно из формулы (5) значения радиусов квантовых орбит сильно зависит от размеров спутника . Вследствие чего для конкретного спутника набор квантовых радиусов орбит будет отличаться от тех значений, которые приведены в таблице 1. Поэтому квантовые орбиты нужно рассчитывать по формуле (5) для каждого спутника отдельно с учетом его реальных размеров.

Те, кто имеет доступ до данных по измерению параметров орбит спутников, могут обработать эти данные с учетом выше изложенного. Много времени на это не потребуется. Но если указанный эффект существует и он заметен, то результаты могут быть интересными.

>