2 Найпростіші випадки зниження порядку в диференціальних рівняннях вищих порядків

Вид материала

Документы

Подобный материал:

• Теми та плани практичних занять з курсу “Вища математика”, 53.52kb.
• Правила диференціювання. Диференціал. Похідні та диференціали вищих порядків. Теореми, 16.56kb.
• Нтд у сучасній теорії диференціальних рівнянь актуальними є питання якісної теорії, 101.01kb.
• Питання з курсу “Диференціальні рівняння”, 59.17kb.
• Секція математичного аналізу та диференціальних рівнянь, 14.84kb.
• План Лінійна однорідна система диференціальних рівнянь з постійними коефіцієнтами Лінійна, 186.96kb.
• Рекомендація, 29.8kb.
• Анал І з захворюваності з твп за 2011рік по комунальній 6 міській поліклініці м. Львова, 74.1kb.
• Висновок про направлення на навчання, 108.26kb.
• Оди), у тому числі наукових досліджень з цих питань, а також заходів, спрямованих, 29.79kb.

2.3. Найпростіші випадки зниження порядку в диференціальних рівняннях вищих порядків

Розглянемо деякі типи диференціальних рівнянь вищого порядку, що допускають зниження порядку.

1) Рівняння не містить шуканої функції і її похідних до 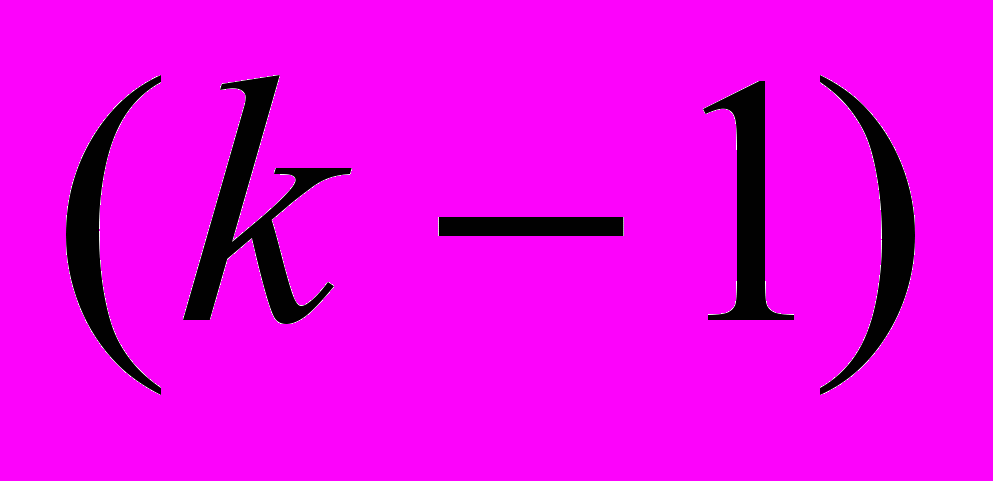-порядку включно

.

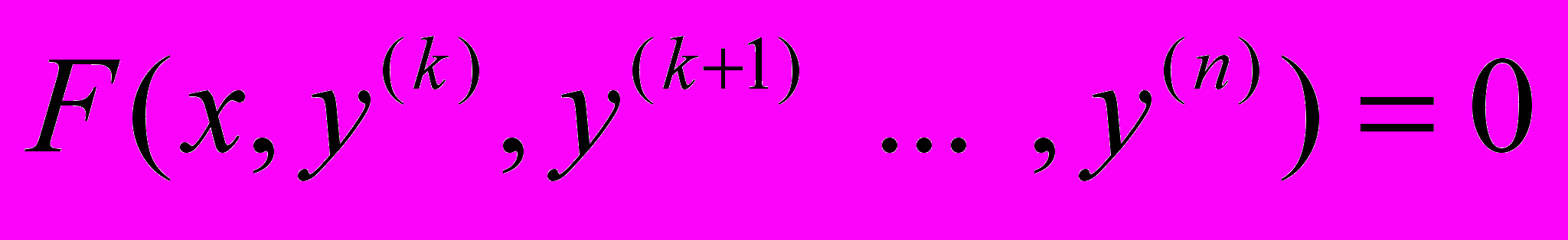Зробивши заміну: ,

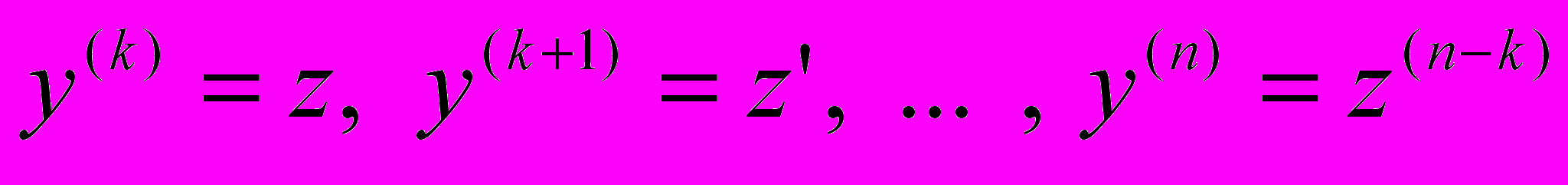одержимо рівняння 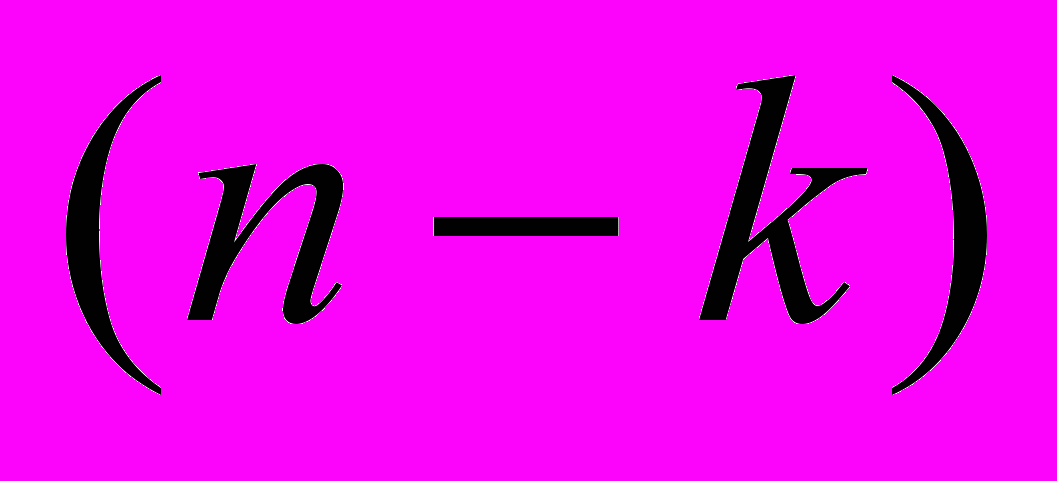-порядку .

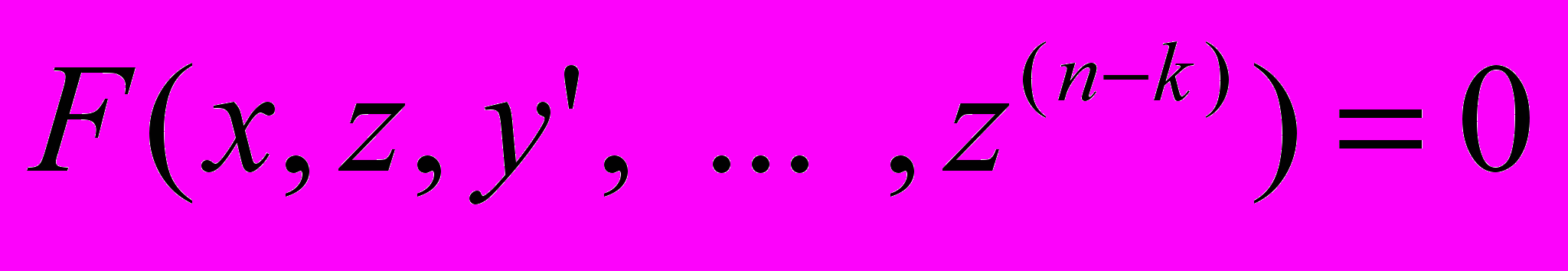2) Рівняння не містить явно незалежної змінної

.

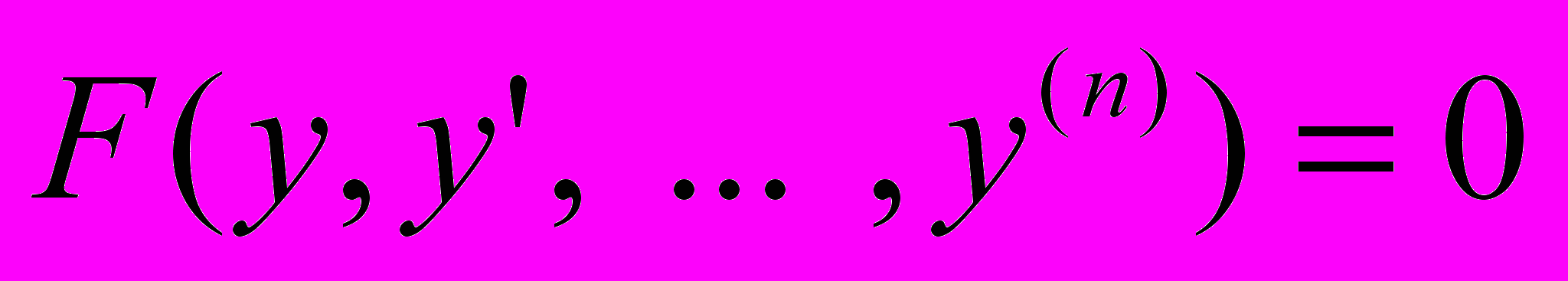Будемо вважати, що 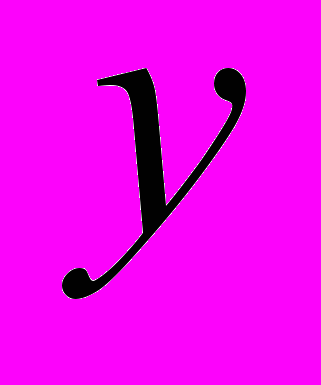- нова незалежна змінна, а - функції від 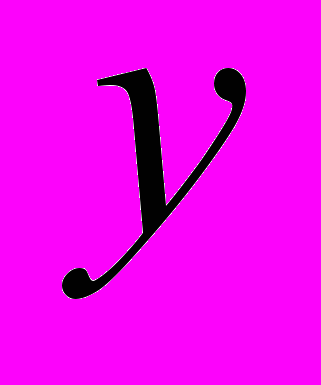. Тоді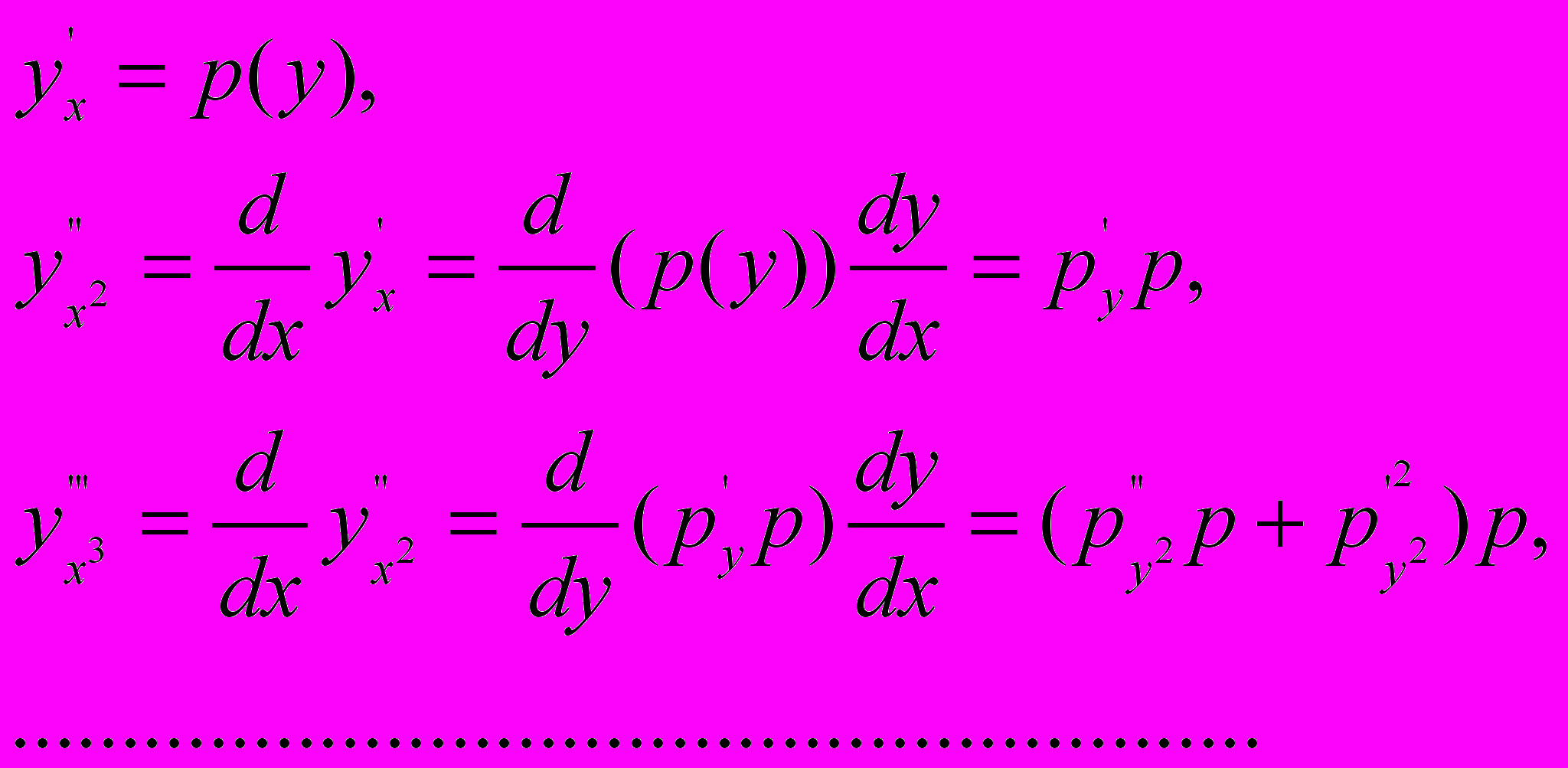



Після підстановки одержимо 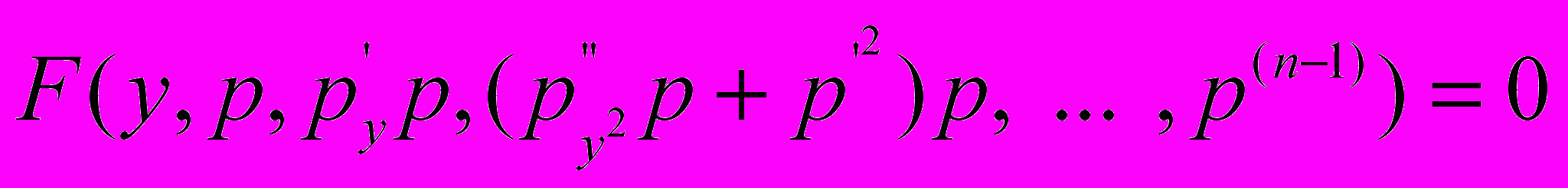диференціальне рівняння -порядку.

3) Нехай функція диференціального рівняння



є однорідної щодо аргументів .

Робимо заміну 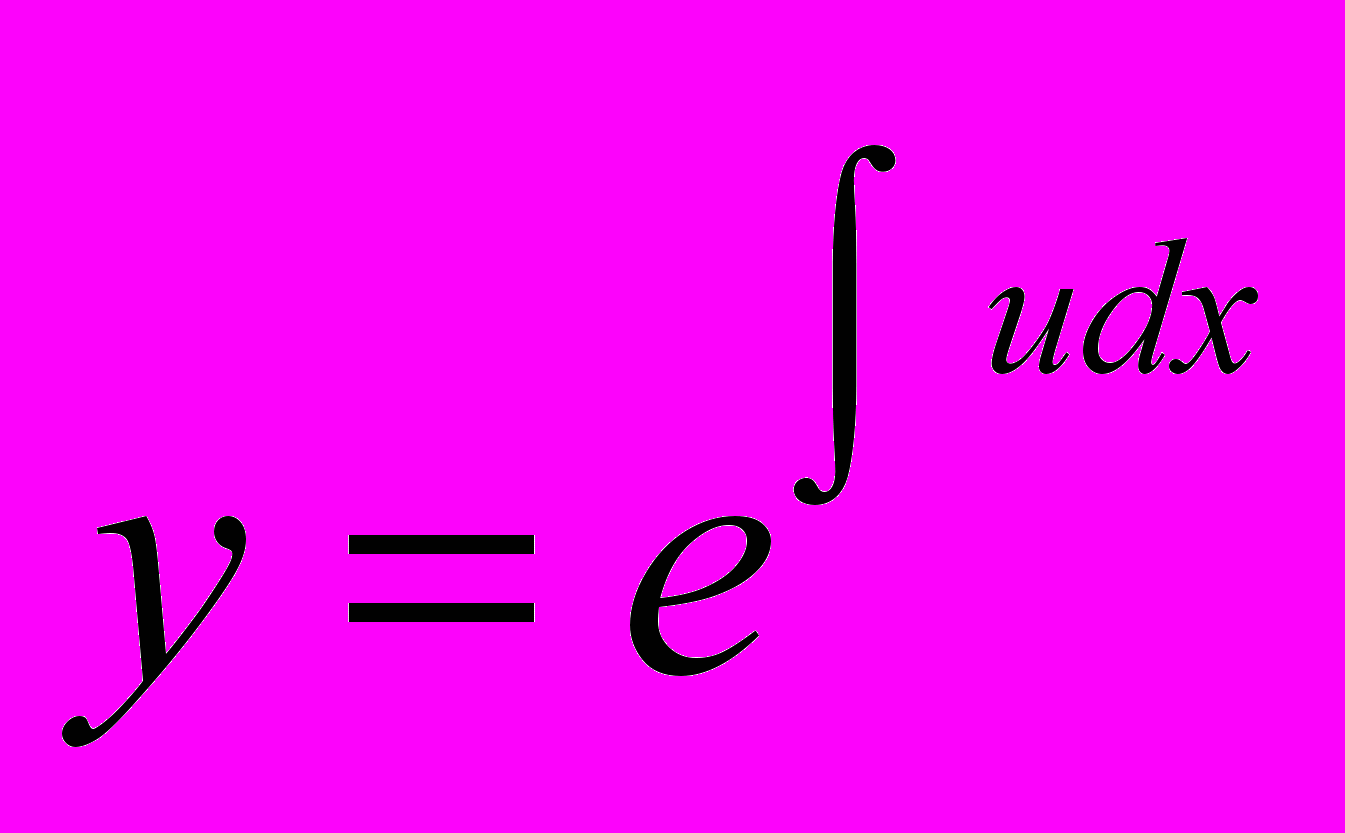, де 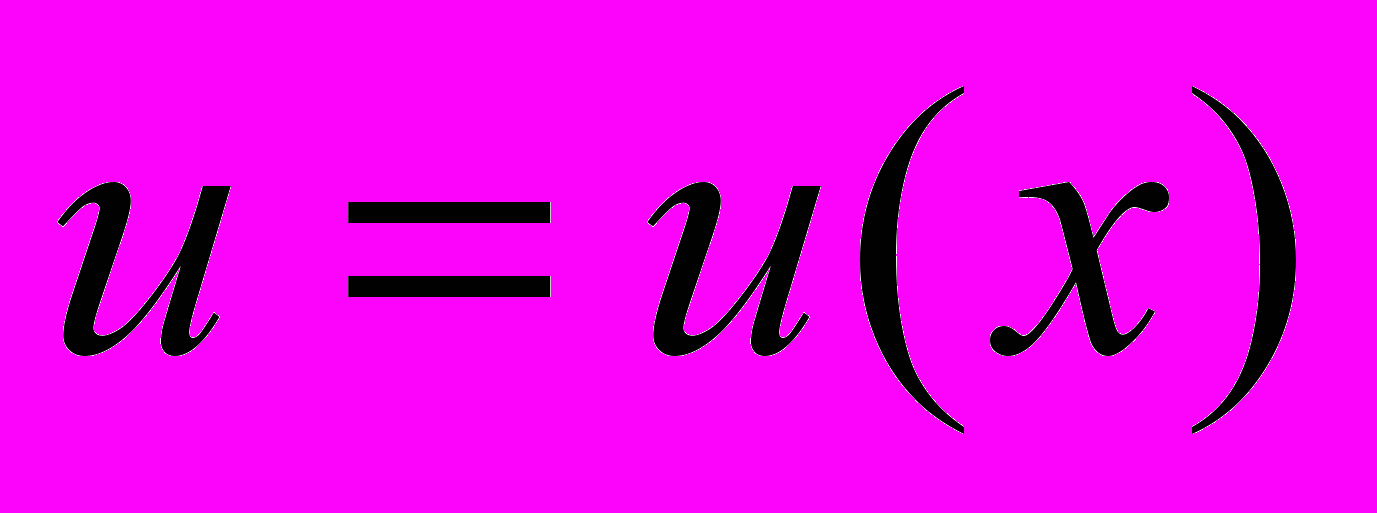- нова невідома функція. Одержимо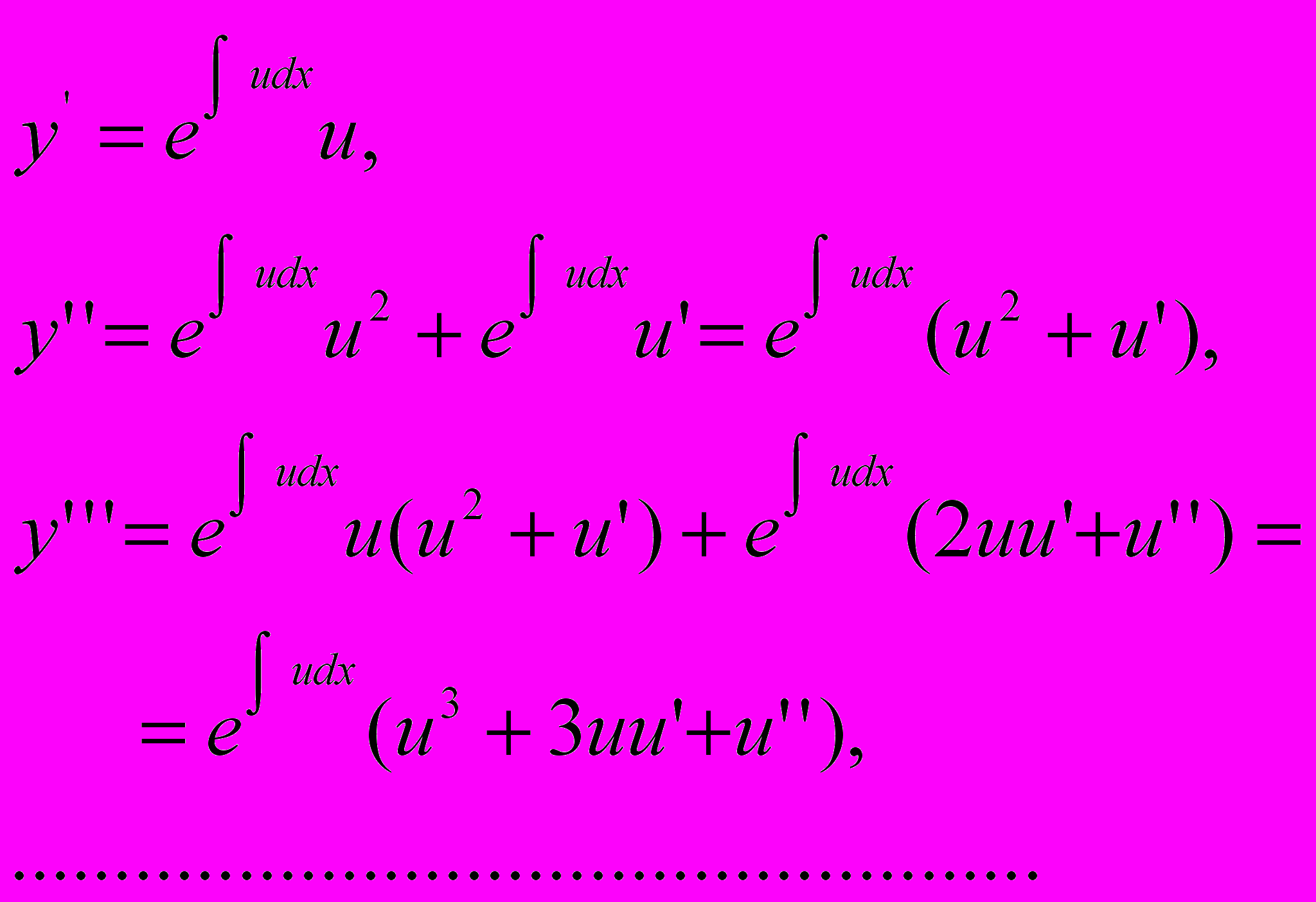



Після підстановки одержимо

.

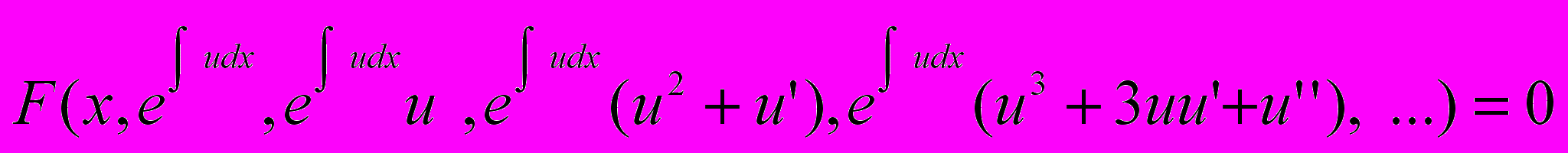Оскільки рівняння однорідне відносно 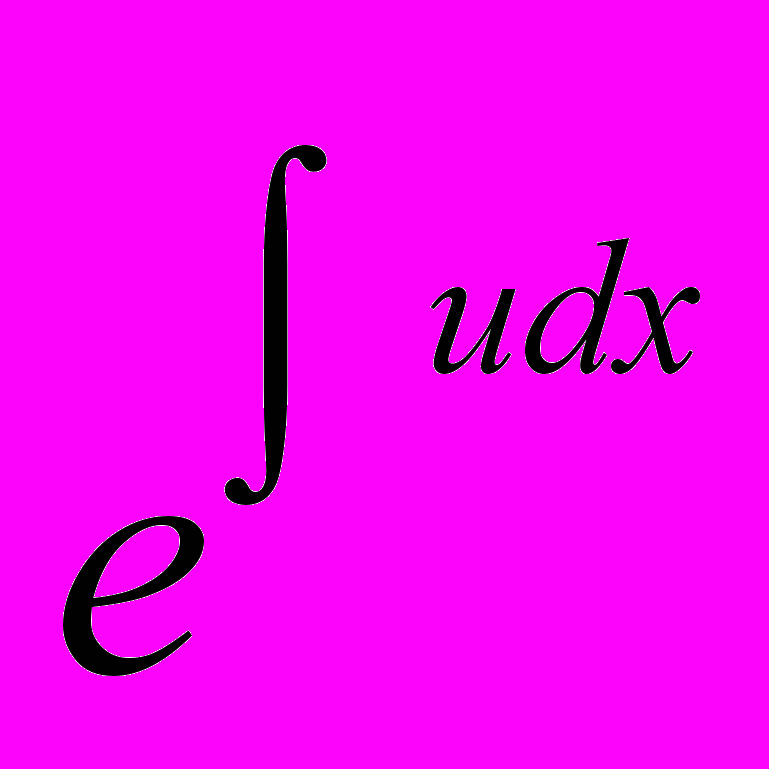, то цей член можна винести і на нього скоротити. Одержимо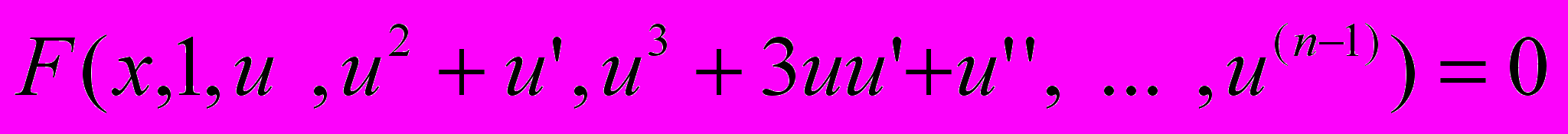



диференціальне рівняння -порядку.

4) Нехай ліва частина рівняння



є похідної деякого диференціального вираза ступеня , тобто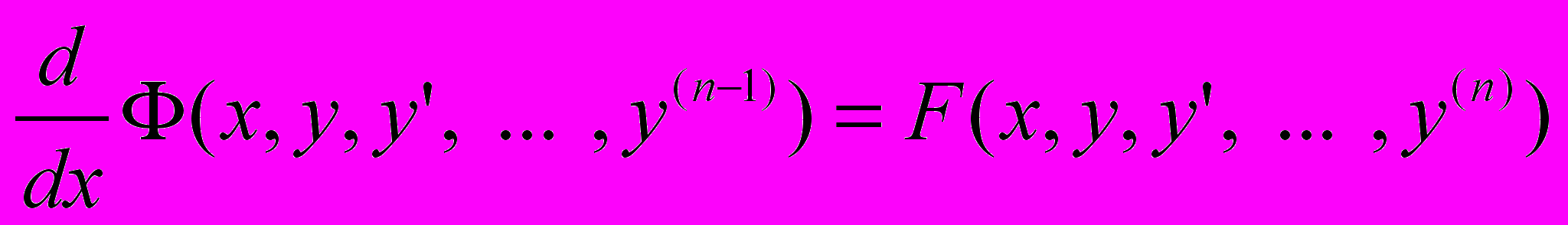

.

У цьому випадку легко обчислюється, так званий, перший інтеграл

.

5) Нехай диференціальне рівняння

,

розписано у вигляді диференціалів



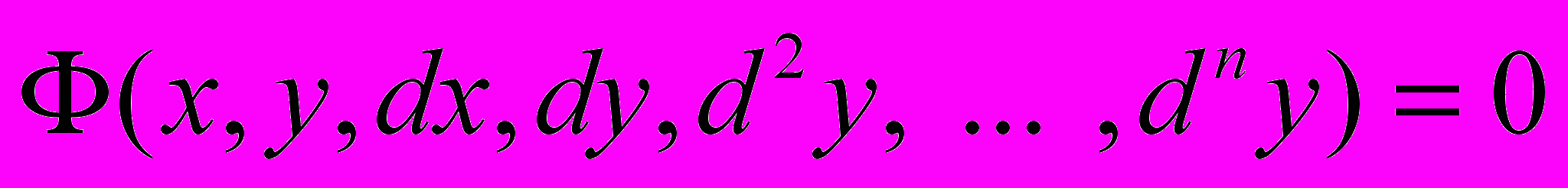
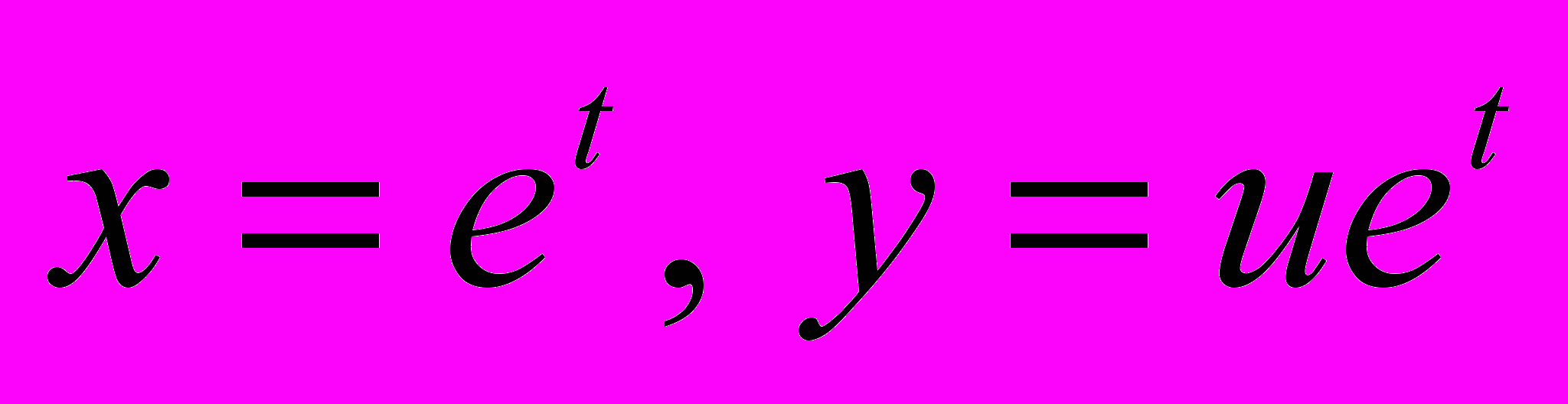і - функція однорідна по всім перемінним. Зробимо заміну , де 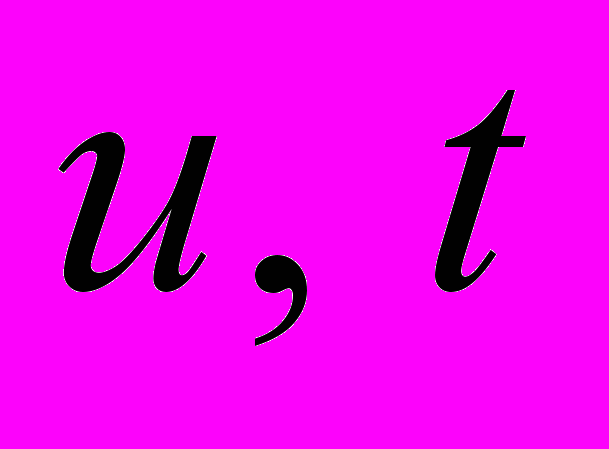- нові змінні. Тоді одержуємо

, ,



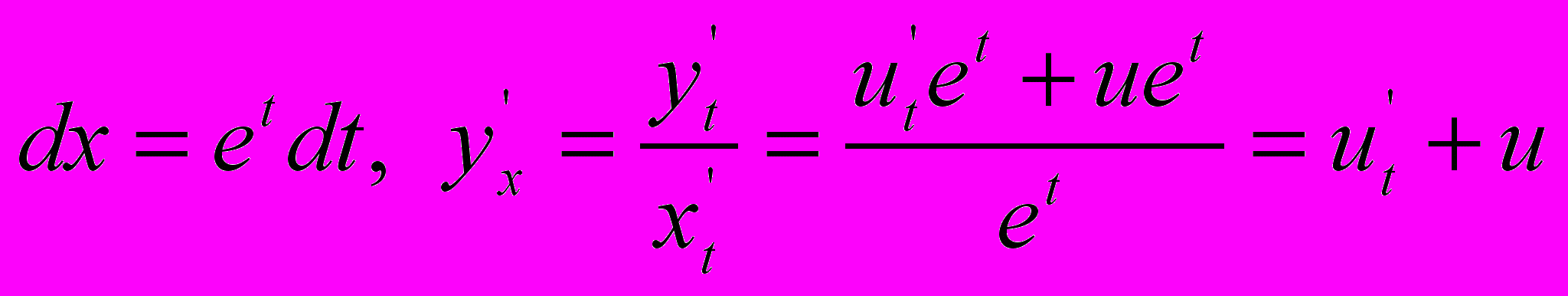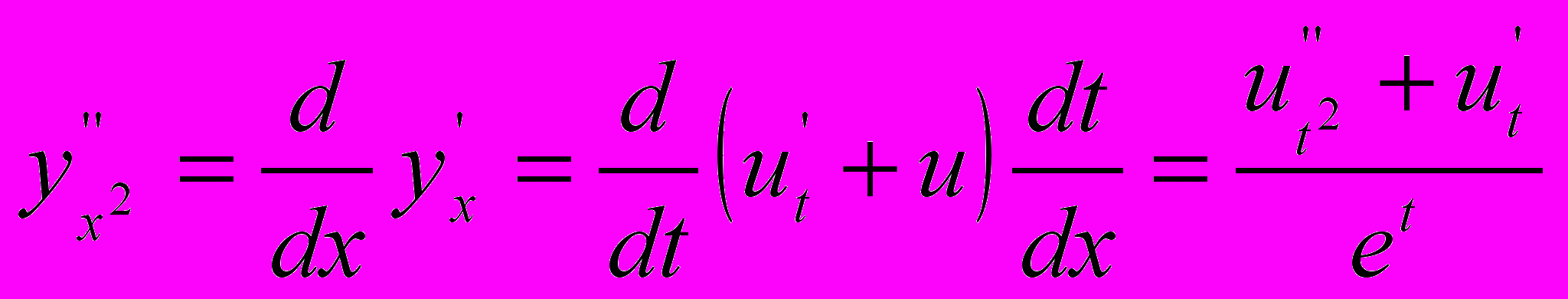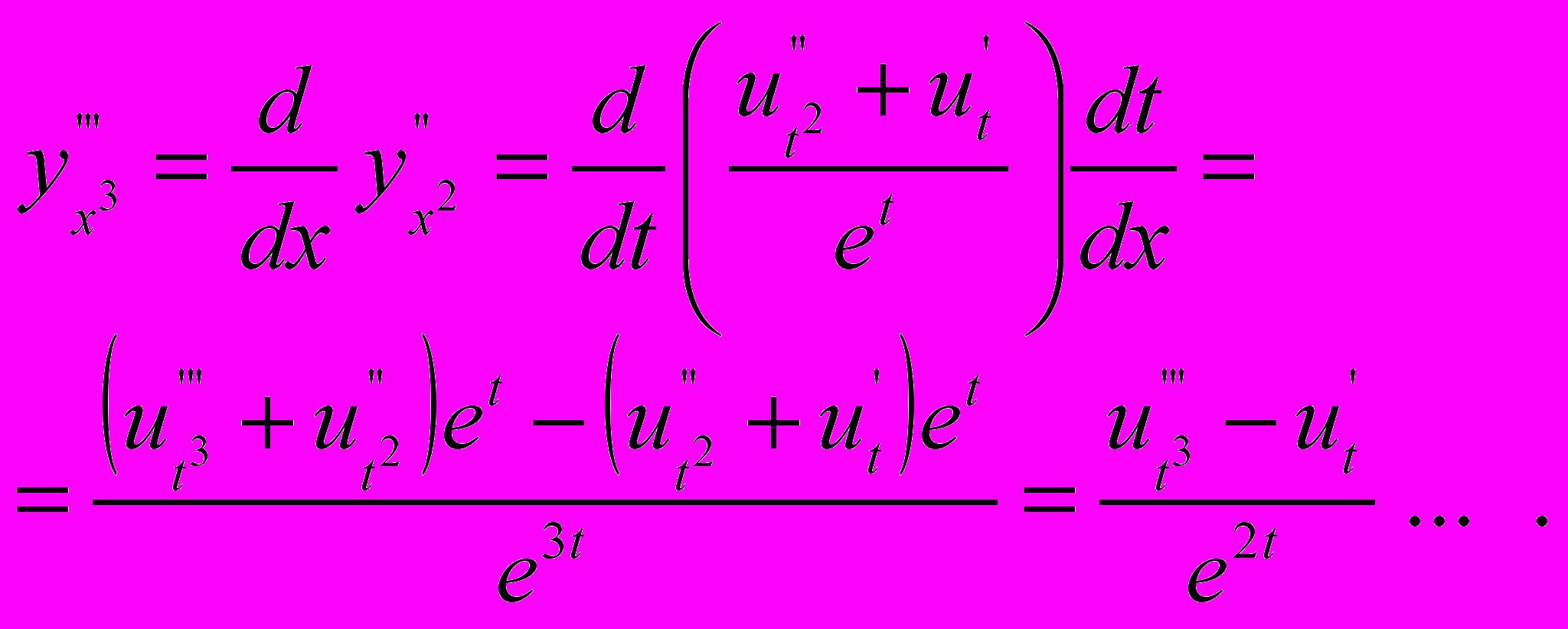
Підставивши, одержимо



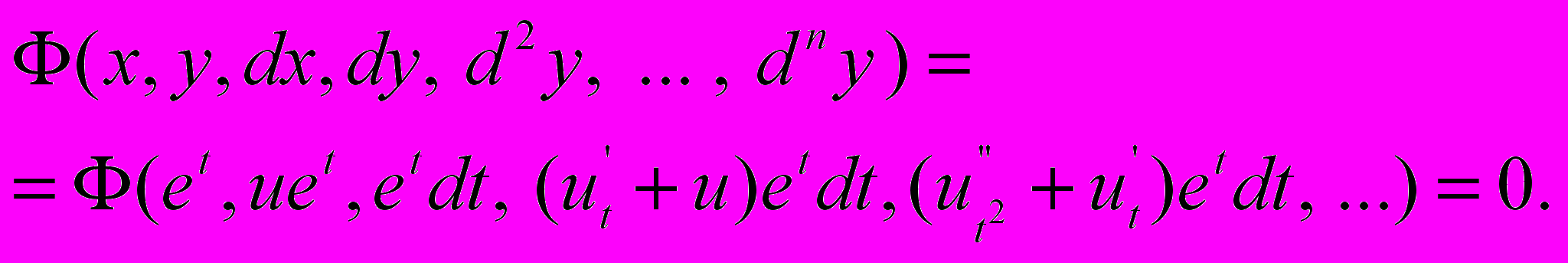
Скоротивши на одержимо .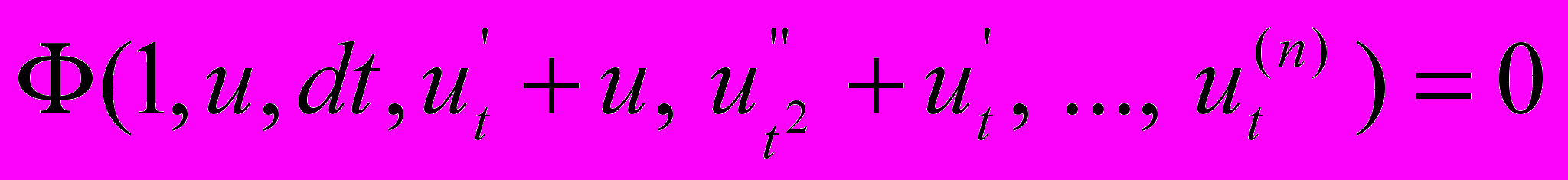

Тобто одержимо диференціальне рівняння, що не містить явно незалежної змінної, або повертаємося до другого випадку.