Geum.ru

Удк 669. 168 Применение математического моделирования для решения задач сложного теплообмена процесса электрокальцинации

Вид материалаДокументы
Подобный материал:
УДК 669.168

ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧ СЛОЖНОГО ТЕПЛООБМЕНА ПРОЦЕССА ЭЛЕКТРОКАЛЬЦИНАЦИИ

Дикарева Алевтина Викторовна, Герасименко Татьяна Евгеньевна


Северо-Кавказский горно-металлургический институт (государственный технологический университет), г. Владикавказ, ул. Николаева, 44, e-mail: dikarka.88@mail.ru


Рассмотрены основные уравнения математической модели процесса электрокальцинации и описаны тепловые и физико-химические процессы, влияющие на формирование кристаллической решетки графита и качество готовой продукции


Электрокальцинаторы являются сложными агрегатами, в которых протекает значительное количество тепловых процессов и физико-химических превращений, сущность которых заключается в развитии и формировании кристаллической решетки графита [1]. Процессы теплообмена, протекающие в электрокальцинаторе, являются основным звеном, которое в значительной степени оказывает влияние на интенсивность и оптимизацию данного процесса. Это связано с тем, что для формирования кристаллической решетки графита электрокальцинация углеродных материалов, в основном антрацитов, проводится при температуре 2000 – 2500 0С.

В электрокальцинаторе взаимосвязаны различные виды теплопередачи в совокупности с локальными источниками выделения тепла. Источником выделения тепла является сам углеродный материал, который выгорает под воздействием высоких температур. Особым вопросом для металлургических процессов в настоящее время является экономия дефицитного топлива и энергетических ресурсов. В связи с этим оптимизация процесса электрокальцинации является актуальной задачей. Однако оптимизировать этот процесс, решая только задачи сложного теплообмена невозможно, так как в кальцинаторе протекает значительное количество физико-химических превращений, влияющих на передачу тепла.

Эффективным методом исследования процессов и определения оптимальных условий его проведения является вычислительный эксперимент, основанный на использовании математических моделей. Сложность рассматриваемых явлений и соответственно описывающих их уравнений математических моделей вынуждает обращаться к численным методам их решения с помощью ЭВМ. В этом случае проведенный анализ носит расчетно-теоретический характер. Поэтому для корректного описания процесса обязательно требуется идентификация математической модели, которая может быть проведена только с использованием практических данных, полученных на действующем агрегате.

Анализ литературных источников показал, что в настоящее время отсутствует полный объем необходимых сведений о процессе кальцинации для точного его описания с помощью математической модели. Это связано с тем, что в электрокальцинаторе взаимосвязаны различные виды теплопередачи в совокупности с локальными источниками выделения тепла, с движением материала и выделением летучих. Для создания комплексной модели необходимо выявить те процессы, которые оказывают определяющее воздействие на конечный результат.

Тепловое поле в электрокальцинаторе во внутреннем пространстве распределено крайне неравномерно, однако установлено, что концентрация силовых линий тока и наибольший разогрев (свыше 2500 0С) проходит в слое материала, расположенном в межэлектродном пространстве вблизи осевой линии (см. рис). Остальной материал нагревается (от 800 до 1200 0С) за счет потока тепла, идущего от центральной нагретой электрическим током зоны к стенкам печи. Часто этого тепла бывает недостаточно для нагрева периферийных участков слоя материала до температуры, обеспечивающей необходимое качество готового материала на выходе из агрегата.

Устранить этот недостаток можно несколькими способами. Во-первых, за счет увеличения количества электроэнергии, затрачиваемой в единицу времени, что регулируется изменением напряжения питания. Во-вторых, за счет скорости перемещения массы материала по объему электрокальцинатора, что регулируется количеством выгрузки прокаленной продукции. И, в-третьих, изменением конструкции внутреннего пространства кальцинатора за счет установки дросселя [2].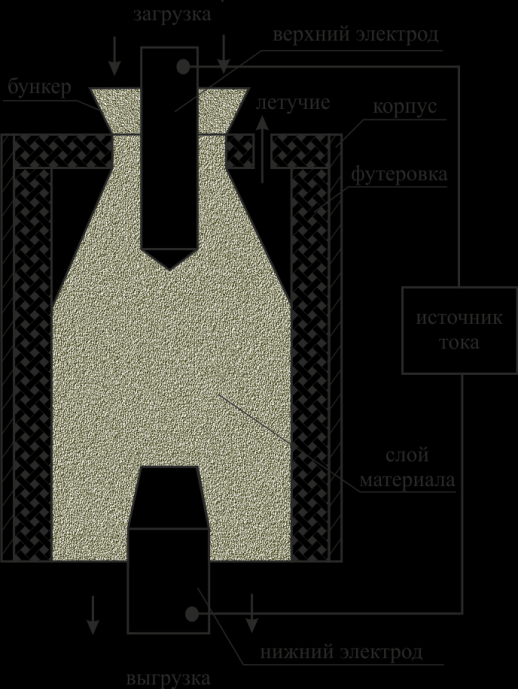


Рис. Схема электрокальцинатора

Однако у каждого из этих способов есть недостатки. Повышение энергетических затрат приводит к увеличению материальных, а понижение скорости перемещения материала или установка дросселя приводят к снижению производительности агрегата. В связи с этим поиск оптимальных режимных и эксплуатационных параметров является актуальной задачей.

Для математического описания процесса кроме базовых свойств материалов необходимо количественно описать комплексный процесс изменения свойств перемещающегося слоя с учетом влияния изменения электрического, теплового, газодинамического полей электрокальцинатора, а также кинетики химических реакций (горения углерода в слое, выделения летучих и т.д.).

Основными физико-химическими свойствами материала, изменяющимися в процессе термообработки, используемыми при оптимизации процесса кальцинации, являются удельная электропроводность (УЭП), теплопроводность, плотность, теплоемкость, степень графитации и содержание летучих.

Электропроводность материала является одной из важнейших характеристик процесса кальцинации и качества продукции. В работе [3], на основе экспериментальных данных, получено интегральное кинетическое уравнение определения удельной электропроводности  и установлено, что рост кристаллов является фактором, определяющим повышение УЭП

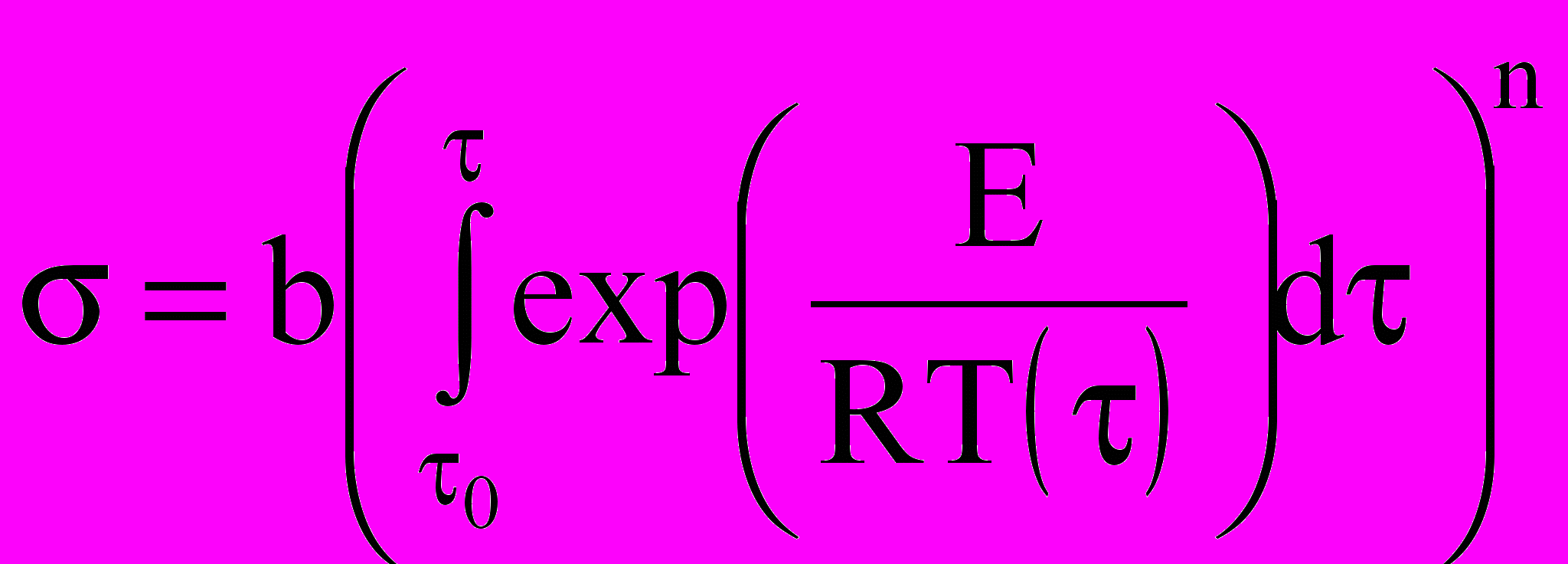(1)

где  - продолжительность изотермической выдержки, мин; Е – кажущаяся энергия активации, кДж/моль; R – универсальная газовая постоянная, кДж/(моль∙К); Т – абсолютная температура, К; b и n – постоянные.

Известно, что существенные колебания значений УЭП возникают в силу неоднородности физико-химических свойств исходного материала, а именно из-за широкого интервала гранулометрического состава, при котором самопроизвольно возникают в объеме зоны с различной газопроницаемостью и, следовательно, с различными температурами. Кроме того грансостав оказывает влияние и на контакт между отдельными зернами материала, при котором электрическая и тепловая энергия переходят от одного зерна к другому. В связи с этим в месте контакта возникает перегрев материала, который оказывает влияние на УЭП в целом. Используя исследования, проведенные в работе [4] можно вывести зависимость УЭП от падения напряжения в точке контакта, температурой перегрева и теплопроводностью материала

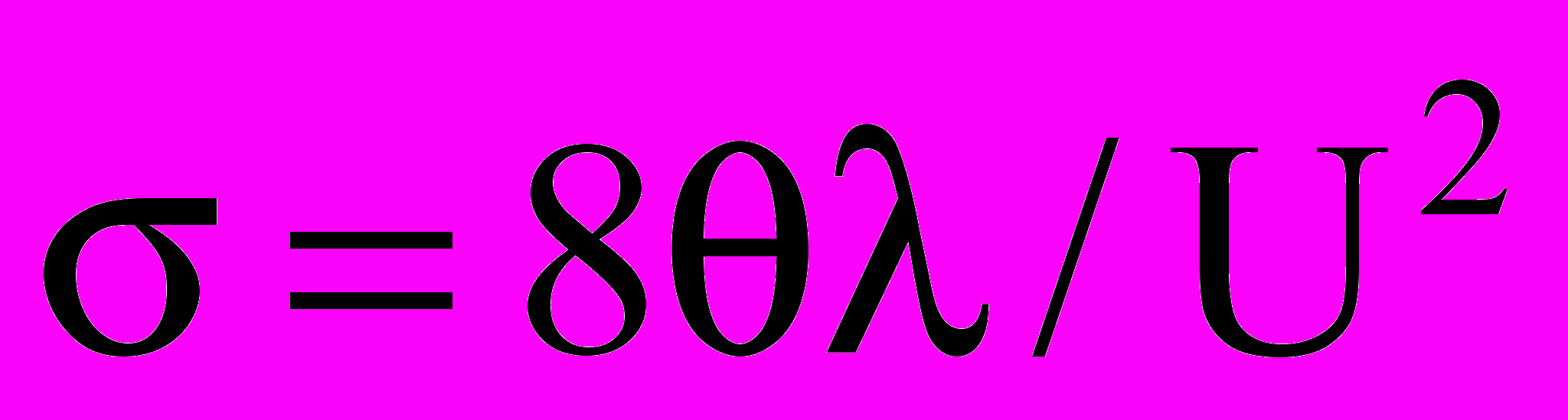(2)

где  - температура перегрева приконтактного места, К;  - коэффициент теплопроводности, Вт/(м∙К), U – контактное напряжение, В.

Другим важнейшим фактором, наряду с УЭП, определяющим работу электрокальцинатора, является эффективная теплопроводность, которая определяется с учетом газовой фазы, расположенной между кусками материала и может быть выражена уравнением 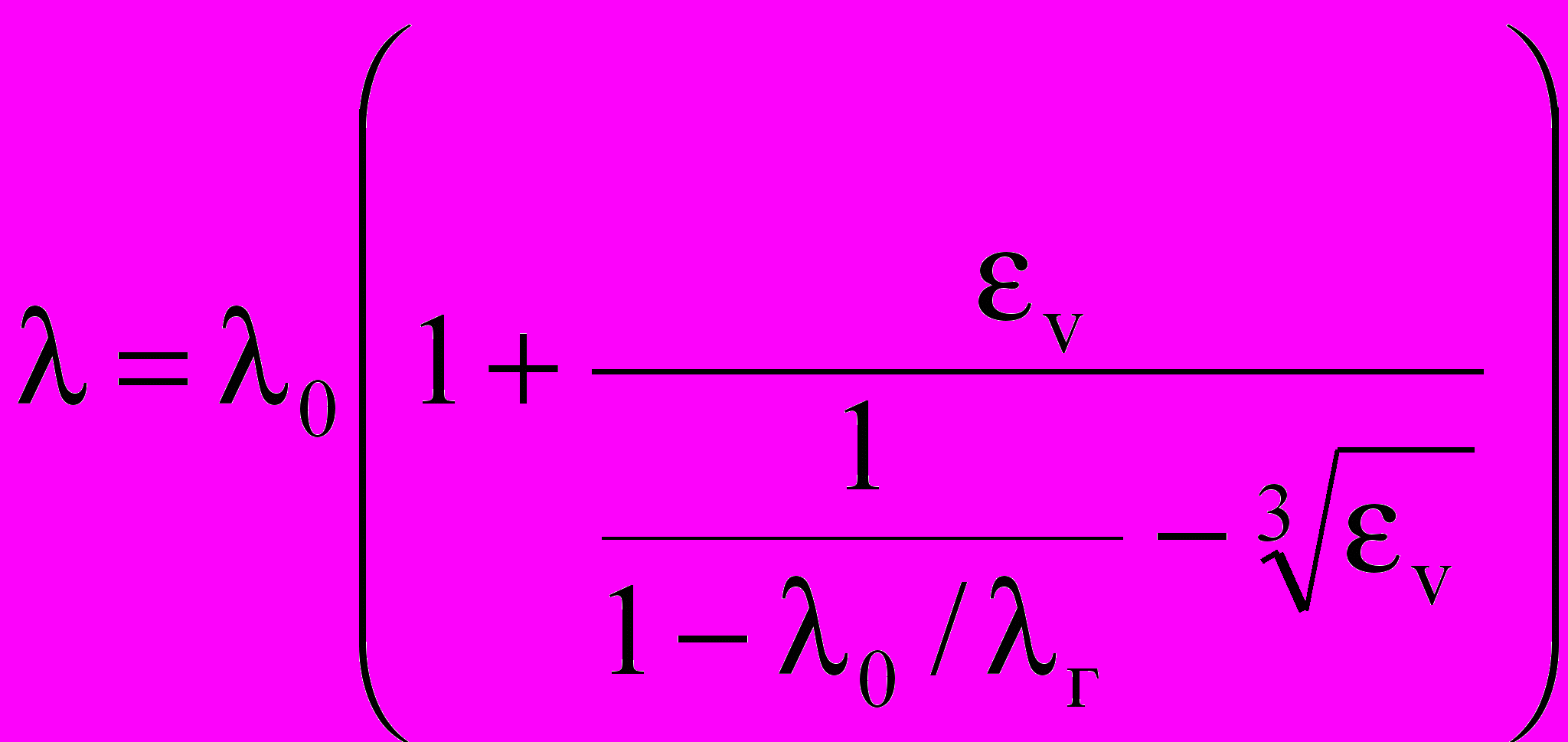[3]

(3)

где 0 и г – теплопроводность материала и средняя теплопроводность газов в пространстве между кусками соответственно, Вт/(м∙К); v – пористость слоя.

Так как электрокальцинатор это агрегат, в котором протекает сложный теплообмен, то помимо теплопроводности необходимо учитывать и конвекцию и излучение. Коэффициент теплопередачи  между поверхностью материала и газовой фазой определяют по уравнению

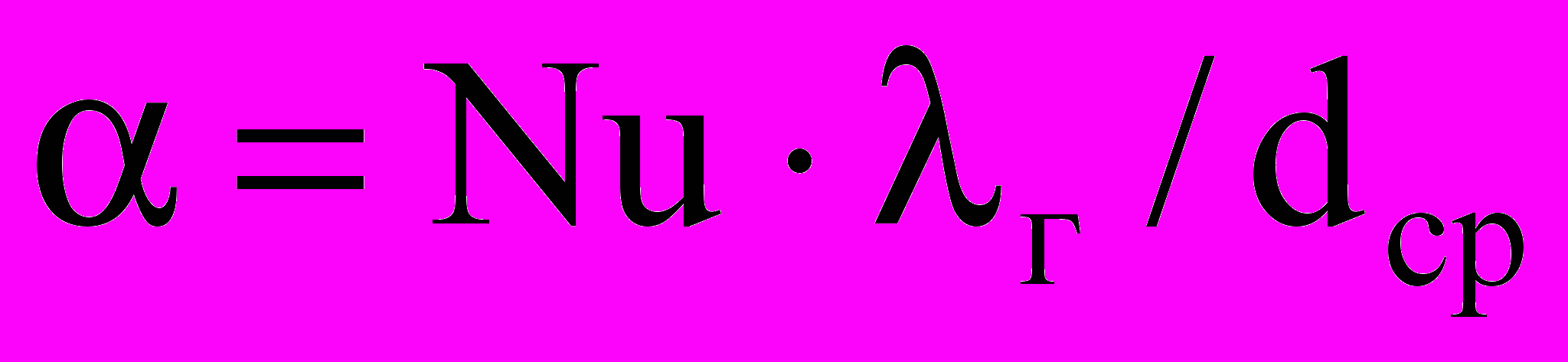(4)

где Nu – приведенное число Нуссельта, dср – средний эквивалентный диаметр кусков материала, м.

Влияние радиационного теплообмена можно определить по уравнению М.М. Гасика для системы свободно насыпанных тел

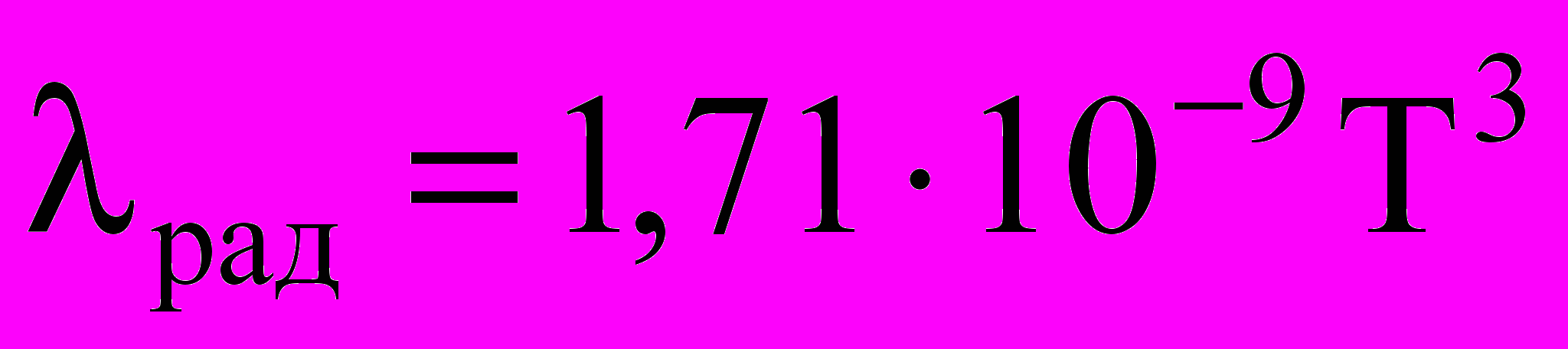(5)

при  = 0,4 и интегральной степени черноты рад = 0,8-0,9, где Т - абсолютная локальная температура материала, К.

Приведенные зависимости позволяют создать математическую модель электрокальцинатора, с помощью которой можно с достаточной точностью получить значительный объем информации, который будет в дальнейшем использован для определения оптимальных режимных параметров и конструкций агрегата, а также практического применения полученных результатов.


Библиографический список

1. Чалых Е.Ф. Технология и оборудование электродных и электроугольных предприятий // М.: Металлургия, 1972.

2. Петров Б.Ф., Кутузов В.А. и др. Физическое моделирование процесса электрокальцинации антрацита // Цветные металлы, № 9, 2006.

3. Гасик М.М., Гасик М.И. и др. Комплексная модель прокаливания антрацита в электрокальцинаторе // Электрометаллургия, № 2, 2007.

4. Лакомский В.И., Быковец В.В. О контактном нагреве термоантрацита в электрокальцинаторе // Цветные металлы, № 1, 2004.


THE APPLICATION OF MATHEMATICAL MODELLING FOR THE PROBLEMS OF DIFFICULT HEAT EXCHANGE ELECTROCALCINATION PROCESS DECISION

Dikareva Alevtina Viktorovna, Gerasimenko Tatyana Evgenjevna

The North Caucasian Mountain-Metallurgical Institute (the State Technological University), 44 Nikolaeva St., Vladikavkaz, e-mail: dikarka.88@mail.ru


The basic equations of mathematical model electrocalcination process are viewed. The thermal, physical and chemical processes which influence the formation of a graphite crystal lattice and the quality of ready-made goods are described.