Московский государственный университет инженерной экологии Кафедра “Высшая математика”

Вид материала

Курсовая

Подобный материал:

• «Московский государственный университет инженерной экологии», 355.46kb.
• Десульфурация нефтепродуктов под действием ультразвука, 270.84kb.
• Влияние типа керамической кольцевой насадки на процесс абсорбции газов, 211.58kb.
• Комплексная утилизация отходов многослойных упаковочных материалов, 211.36kb.
• Организационно-экономические и институциональные основы ресурсного обеспечения развития, 611.9kb.
• Московский Государственный Университет Инженерной Экологии доклад, 94.99kb.
• Московский Государственный Институт Электроники и Математики (Технический Университет), 763.07kb.
• Темы курсовой работы по дисциплине "дискретная математика" (Приложение к рабочей программе, 128.96kb.
• Московский Государственный Институт Международных Отношений (Университет) мид россии,, 39.44kb.
• Закатов Владислав Павлович Оглавление московский государственный институт международных, 623.88kb.

Московский государственный университет инженерной экологии


Кафедра “Высшая математика”


Курсовая работа №3


Вычисление тройных и криволинейных интегралов


Группа М-23

Студент:

Калимулин А.

Преподаватель:

Еникеев И.Х.


Москва 2005

З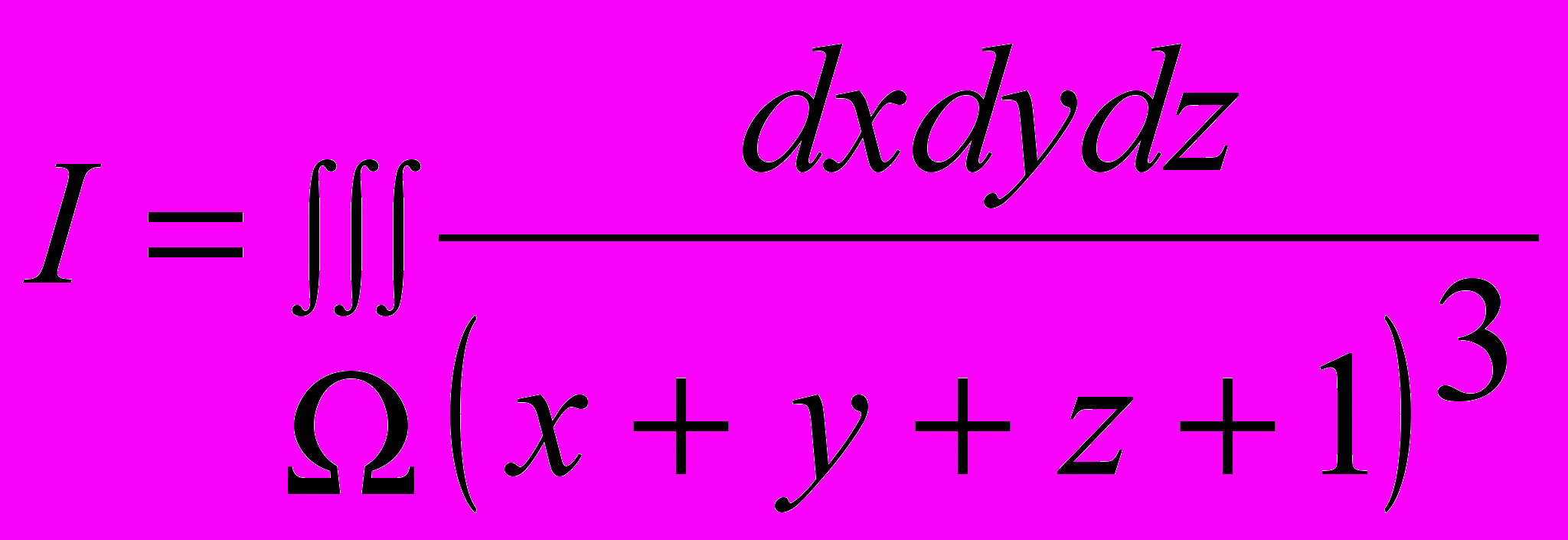адача №1 вычислить интеграл:


Где область имеет вид: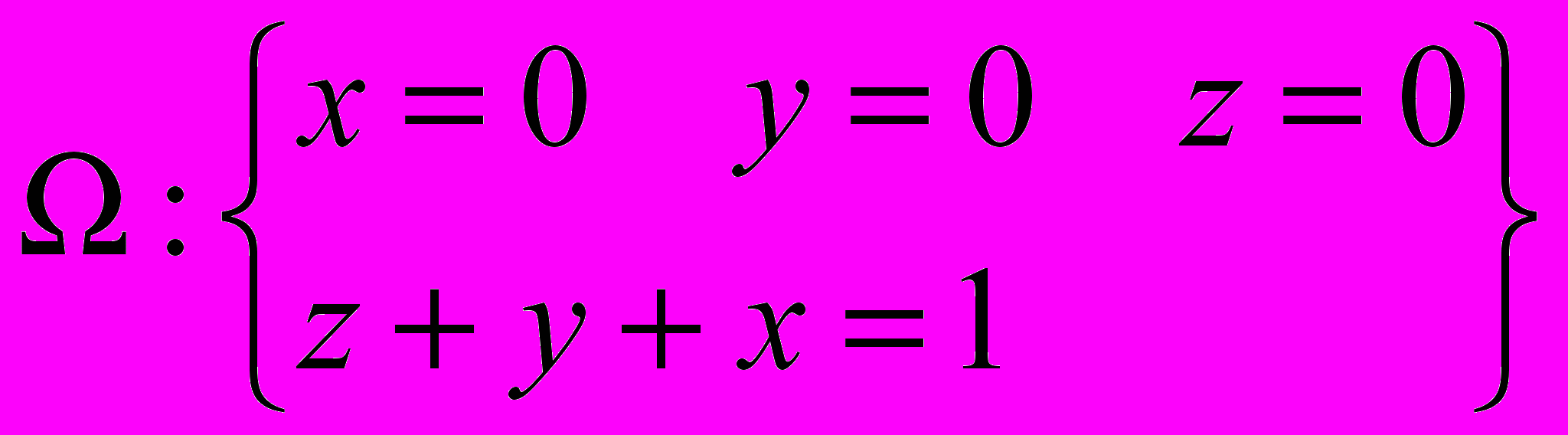

Решение:

Область - пирамида с вершиной в точке О и гранями 1,1,1:

Н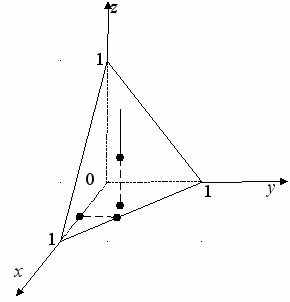аходим уравнение плоскости:

Z=1-x-y

Определяем пределы интегрирования

и 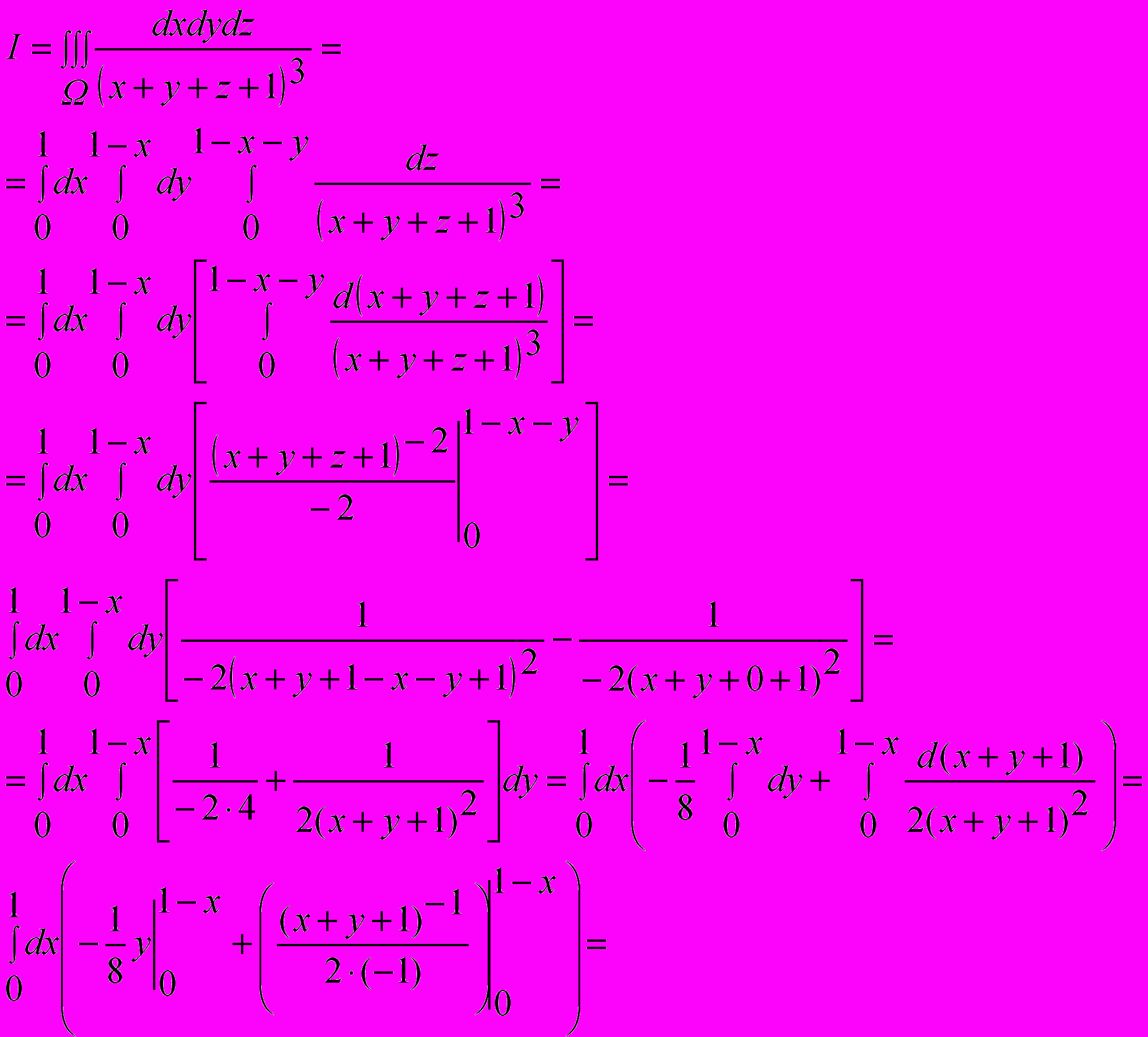решаем данный тройной интеграл:




Ответ:


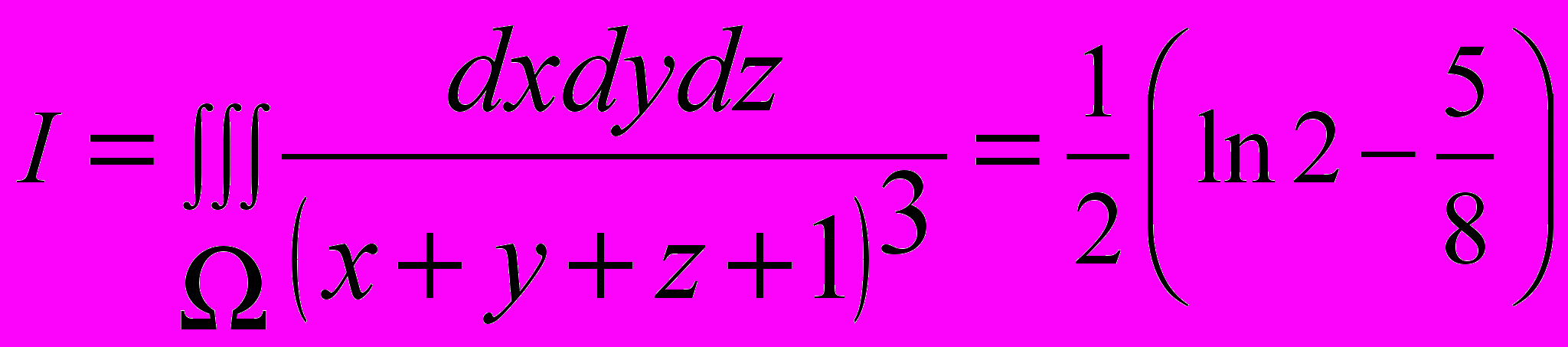
Задача №2 Вычислить в цилиндрической системе координат тройной интеграл: , Где область


П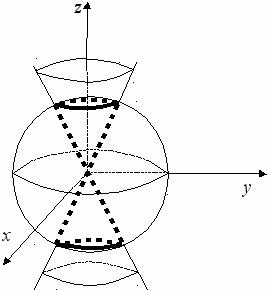оскольку - тело вращения вокруг

Оси Z , удобно перейти к цилиндрическим

координатам:



при этом , а искомый

интеграл будет определяться формулой





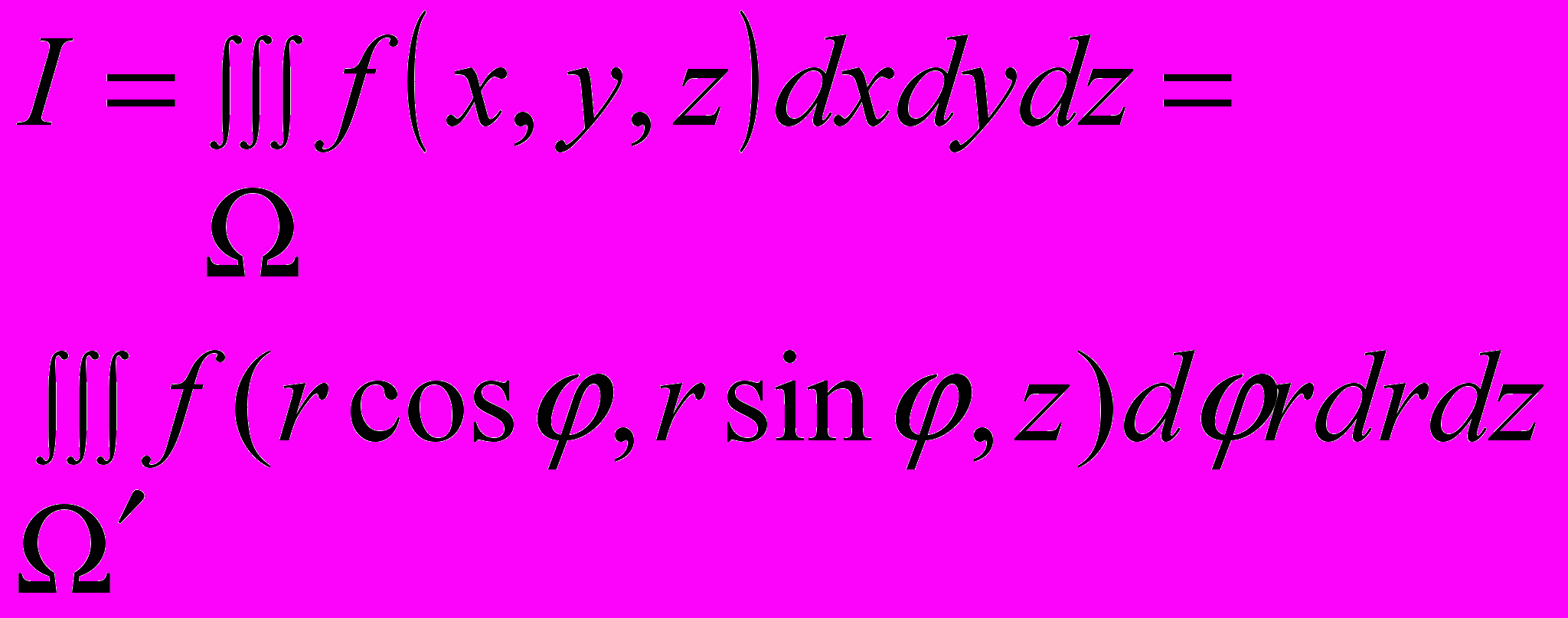
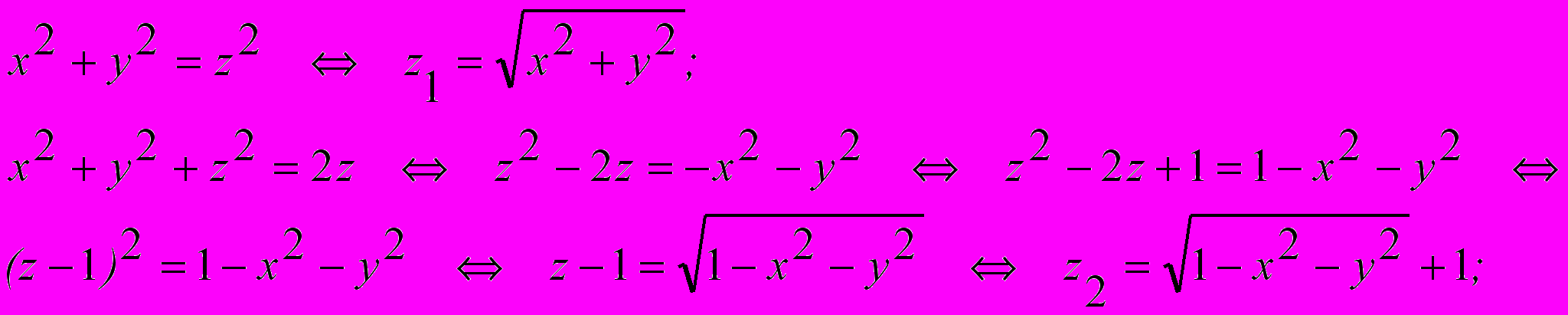
Зададим область неравенствами:
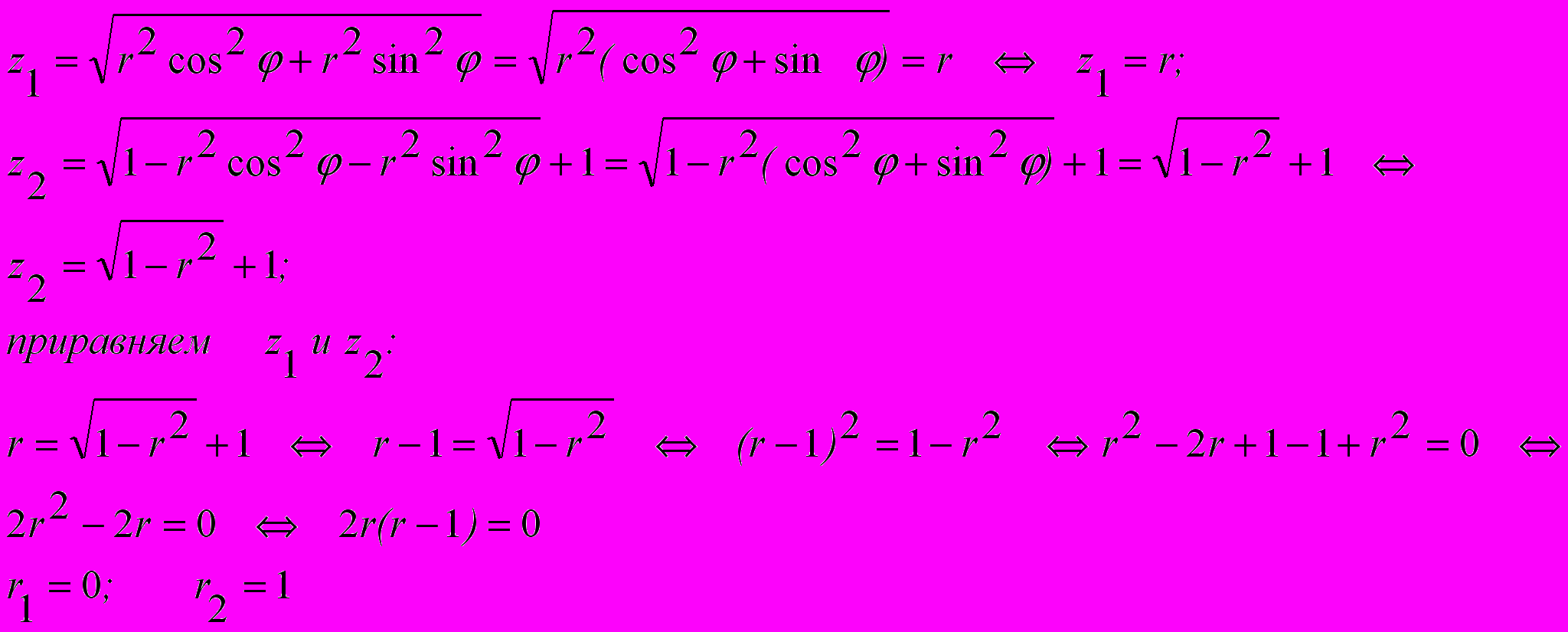определим какая функция больше на промежутке :

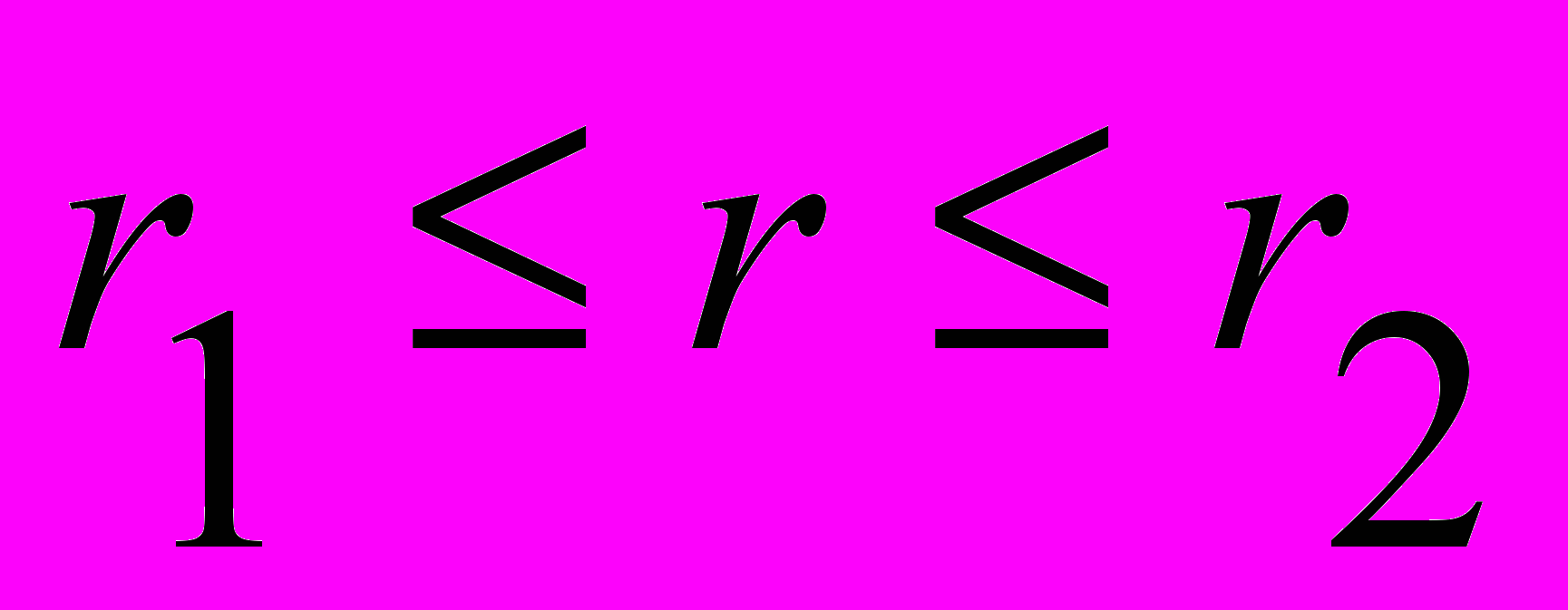на этом промежутке.

Тогда область определяется системой неравенств: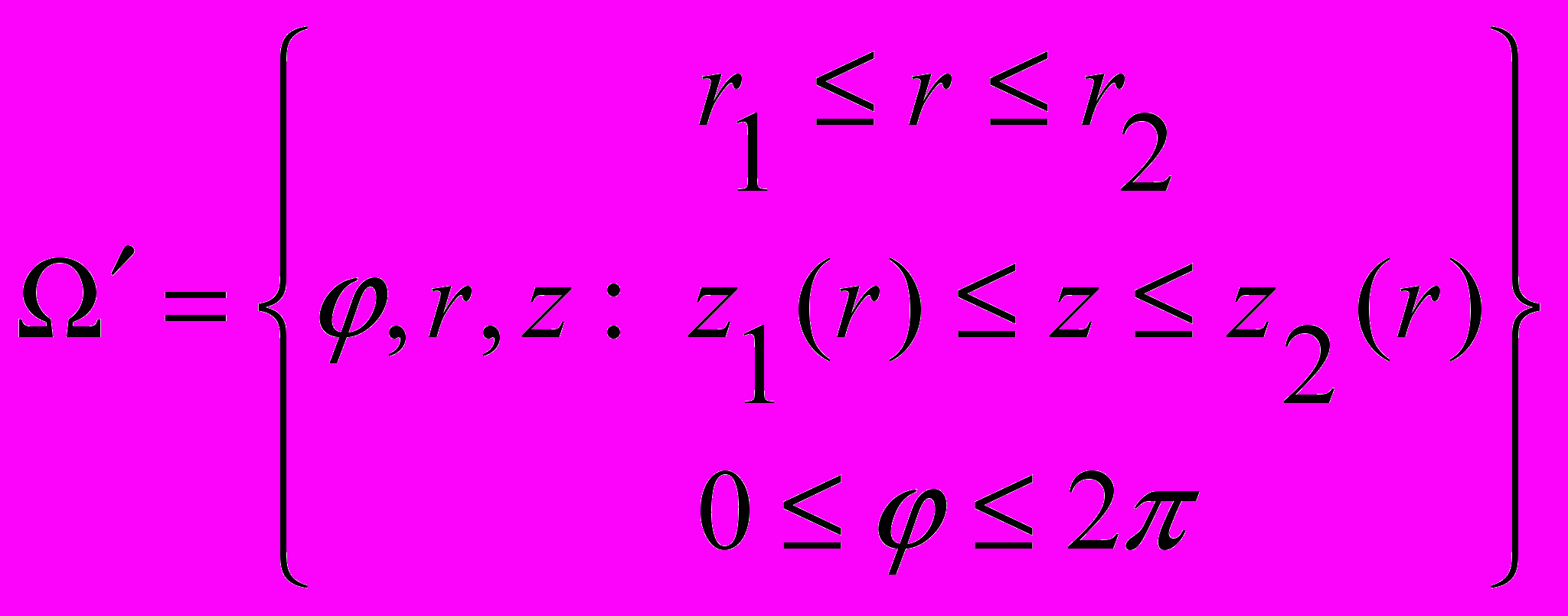



переходим от тройного интеграла к повторному:



Ответ:


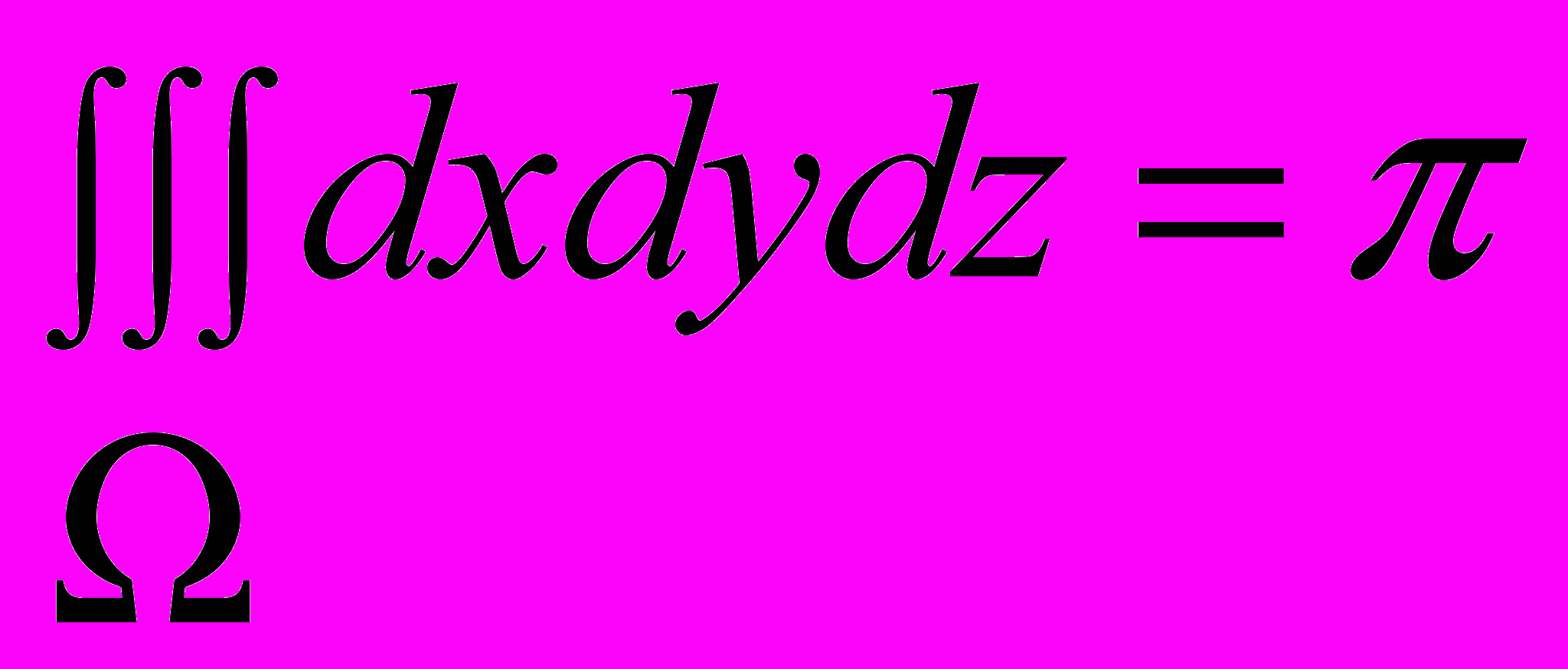
Задача №3 Вычислить интеграл по контуру L:



Решение:

Изобразим график функции

Определим производную этой функции:



Тогда:



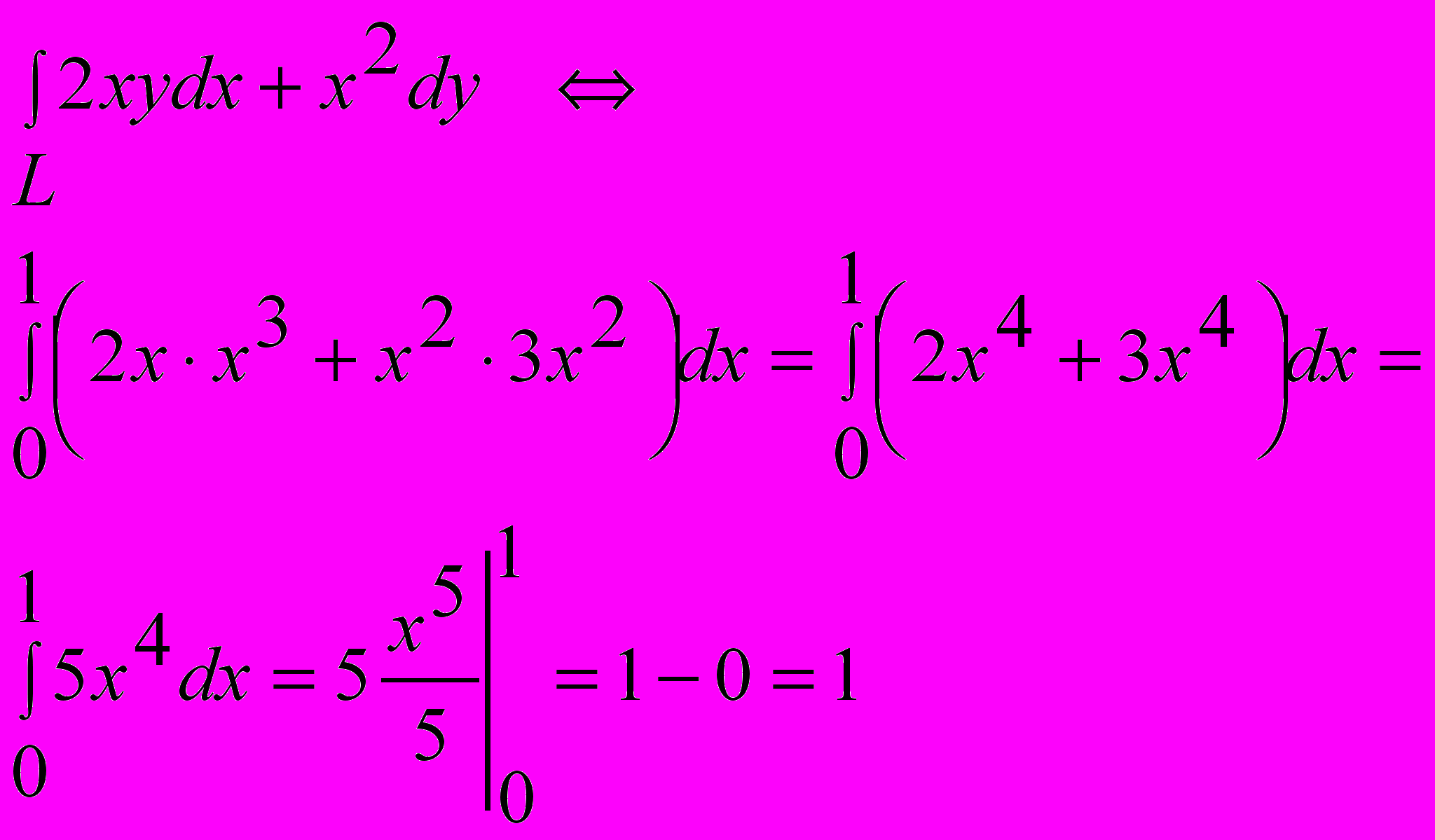
Ответ:

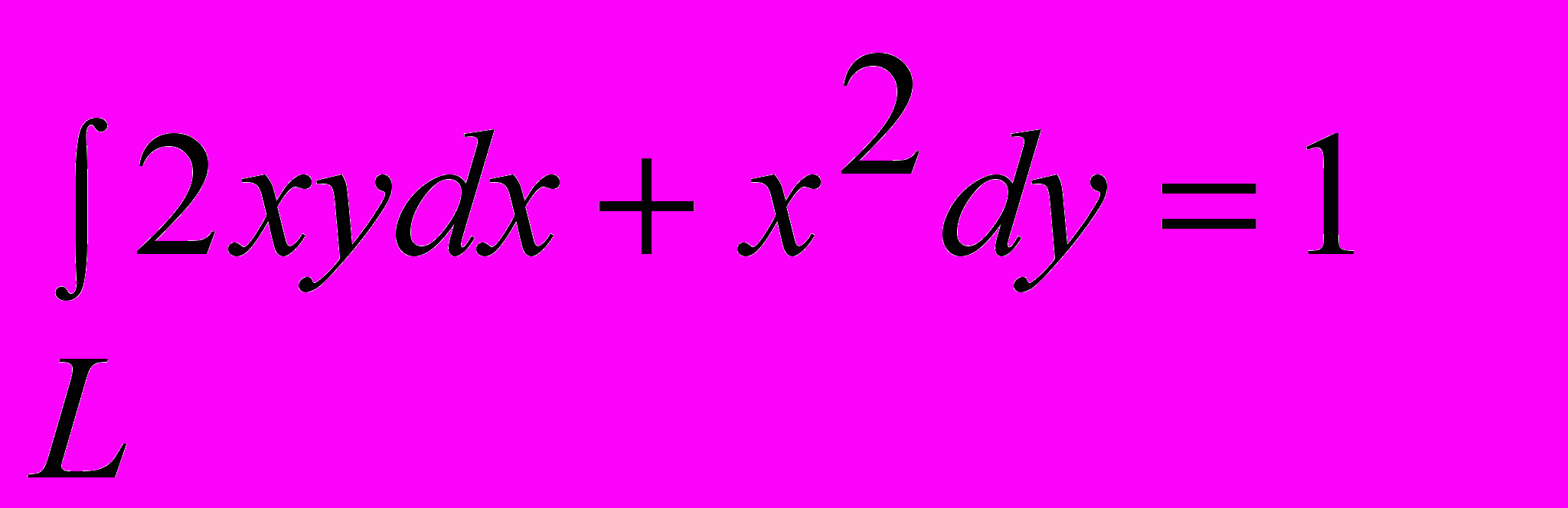
З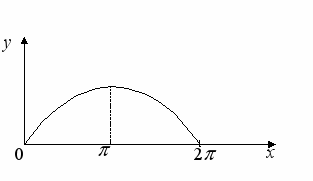адача №4 Вычислить интеграл 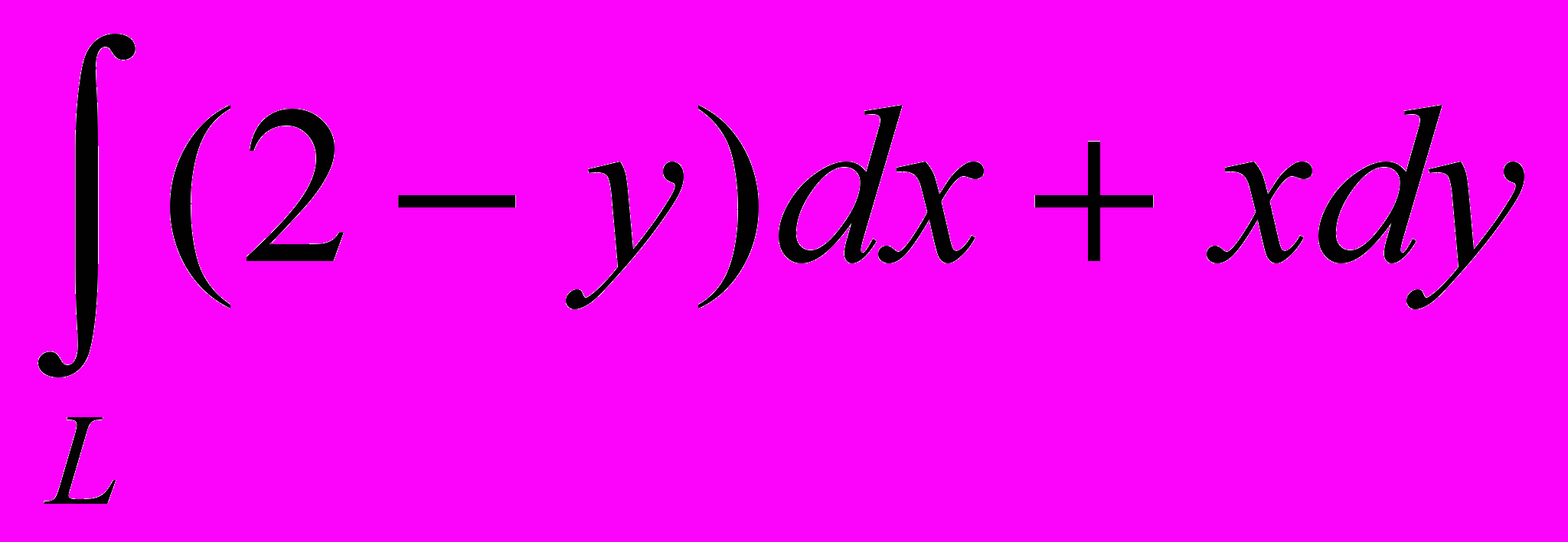по контуру L, заданному параметрически.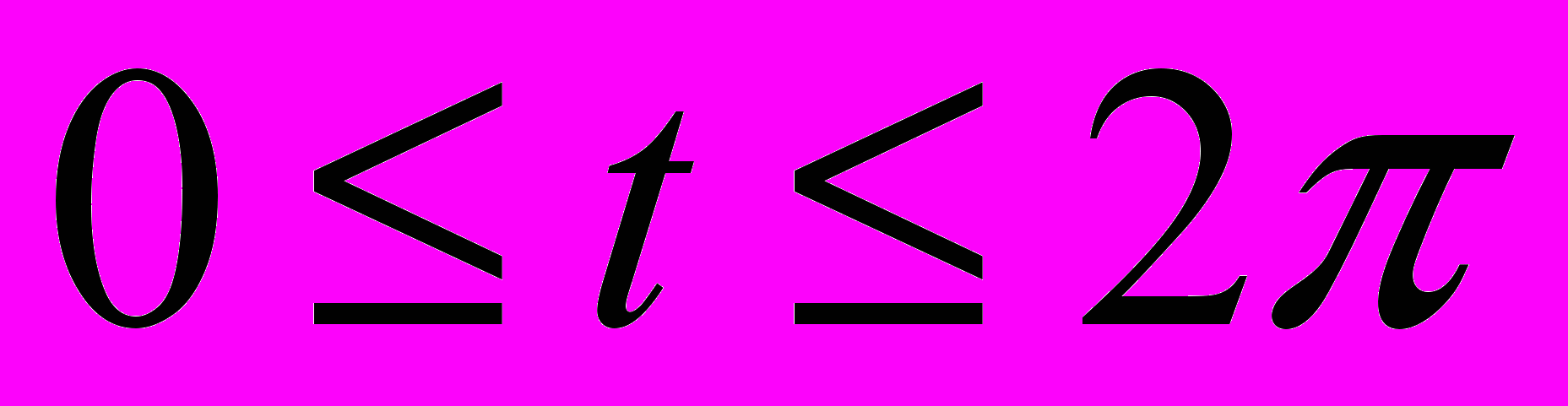



определим производные функций:



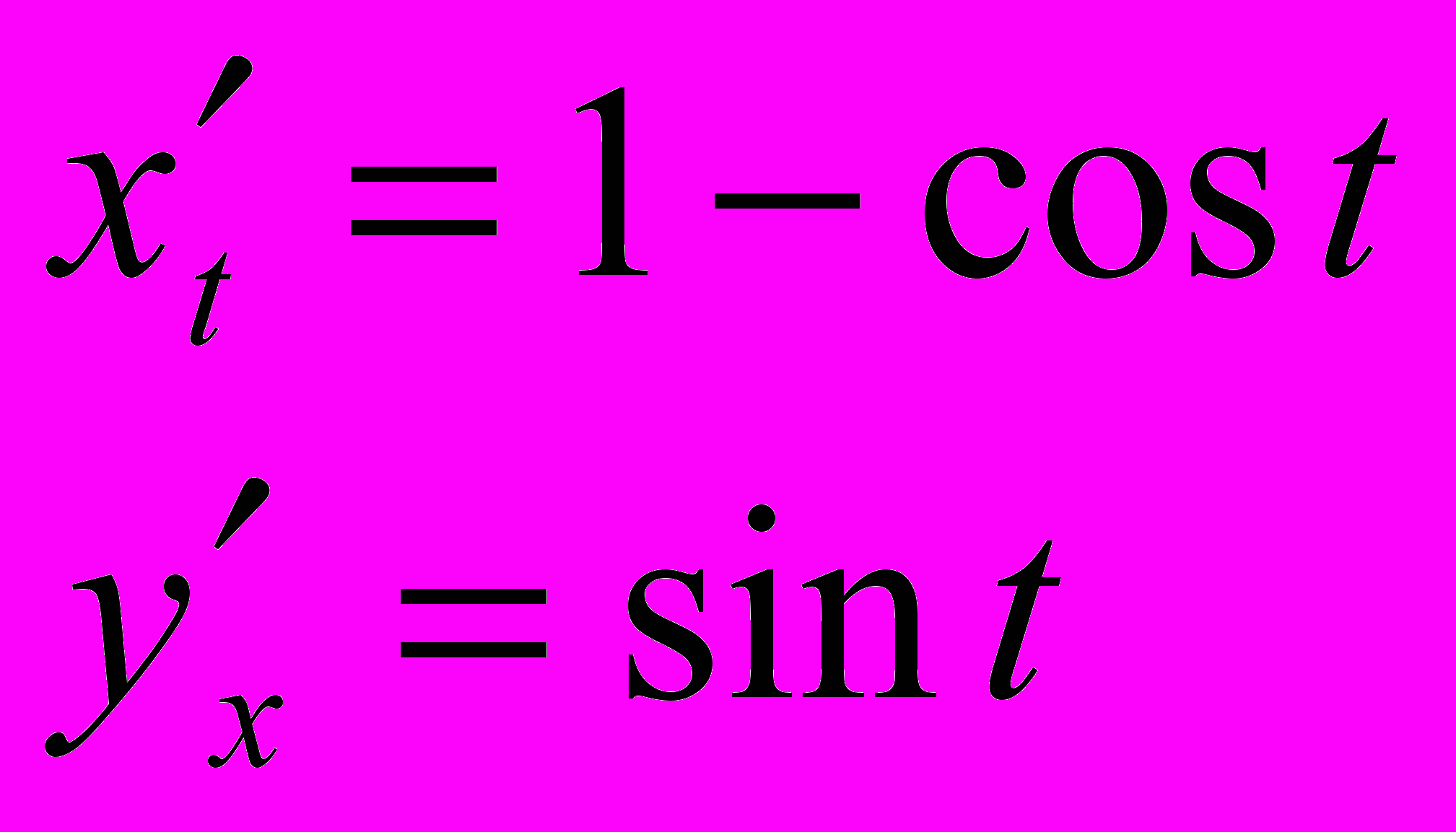
Согласно формуле:

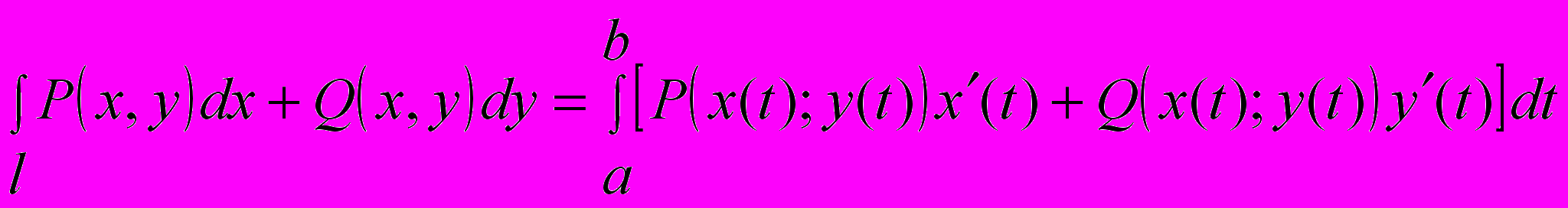
Интеграл 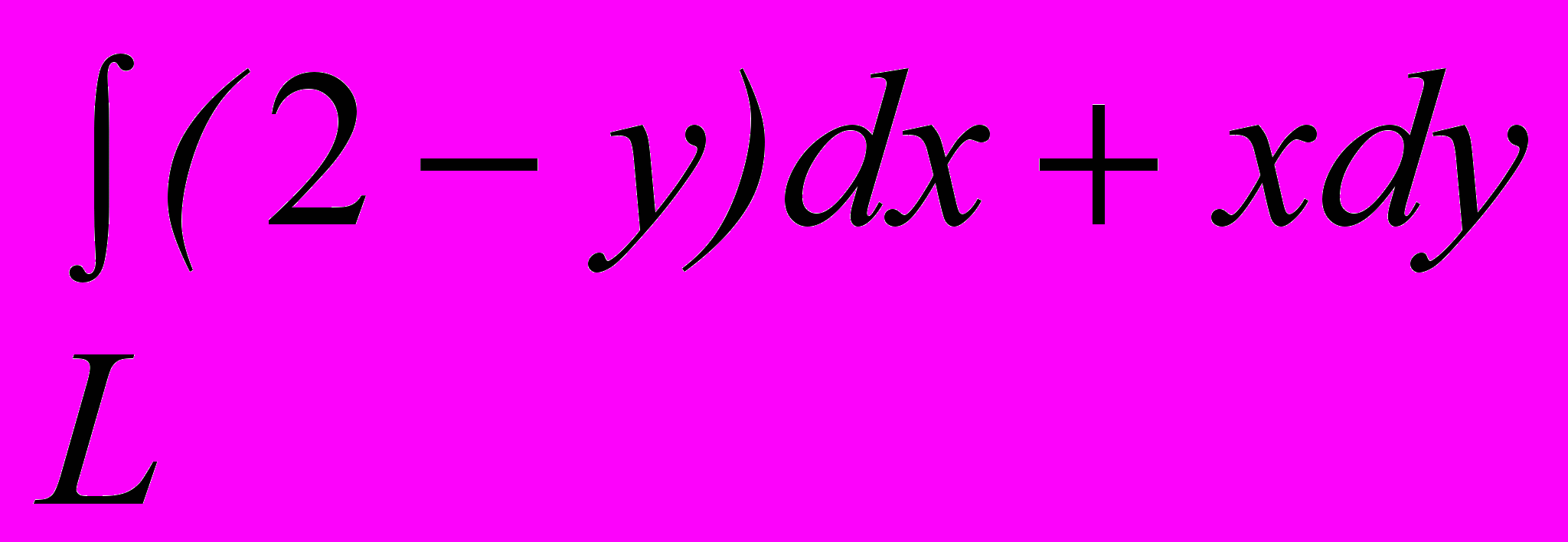примет вид: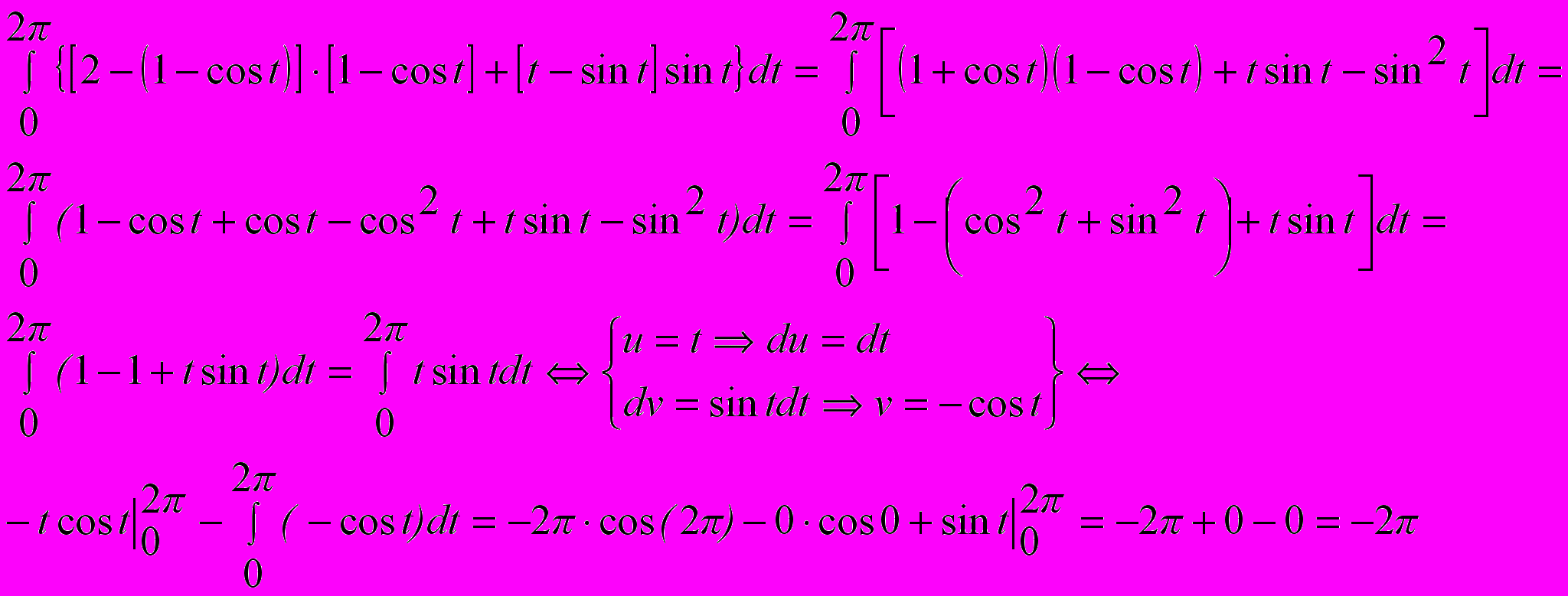

Ответ:


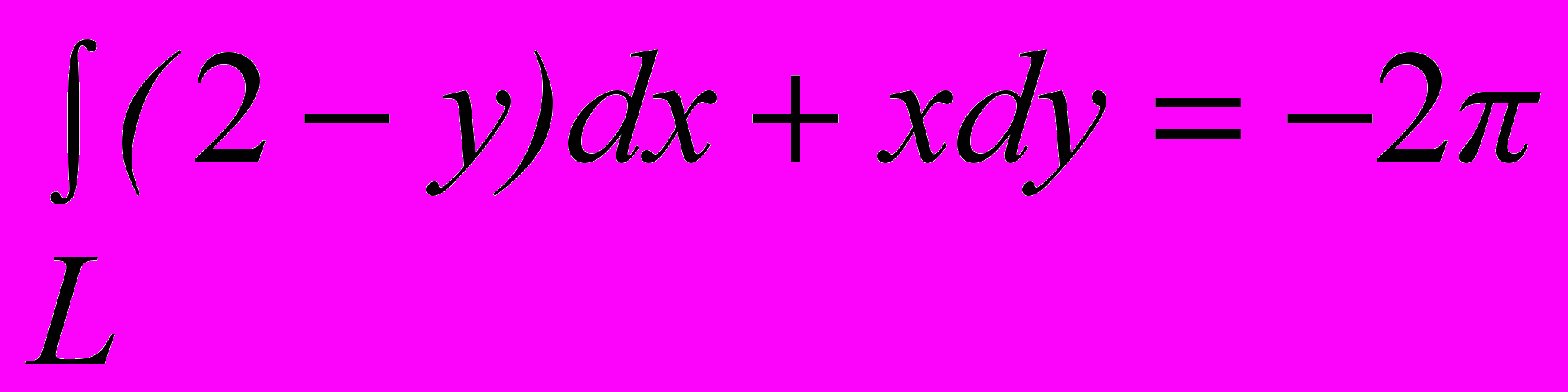
Задача №5

При помощи формулы Грина вычислить интеграл:



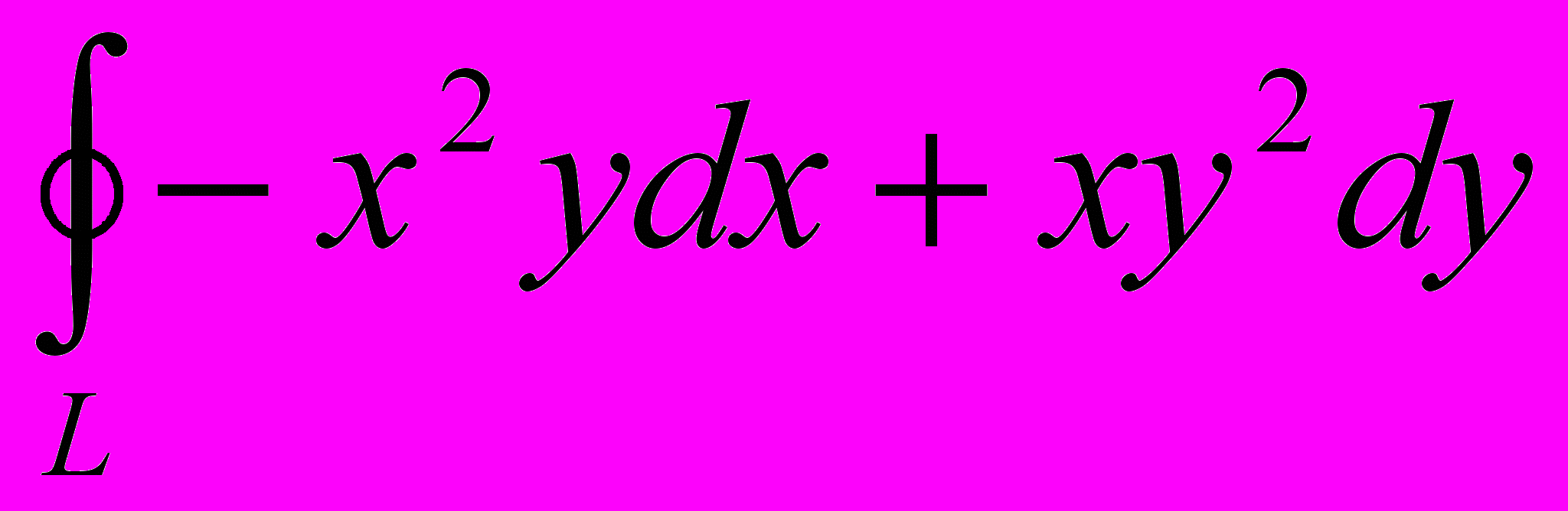
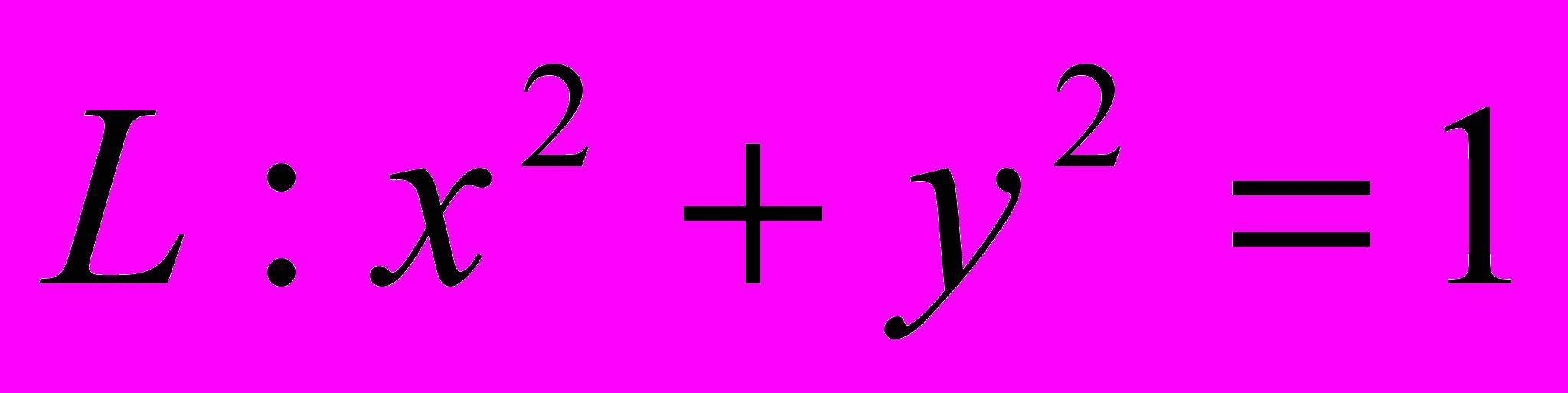
Решение

Согласно формуле Грина:



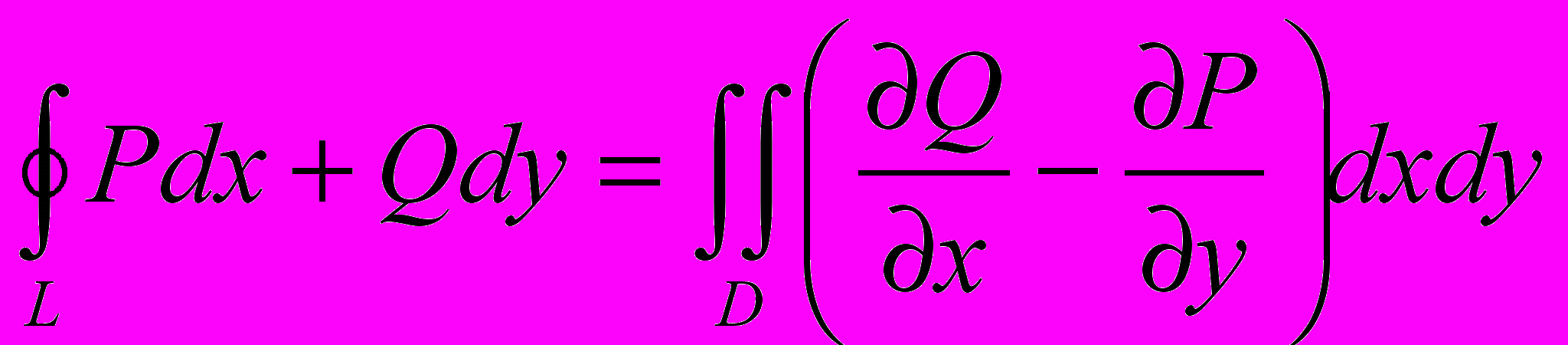
, тогда: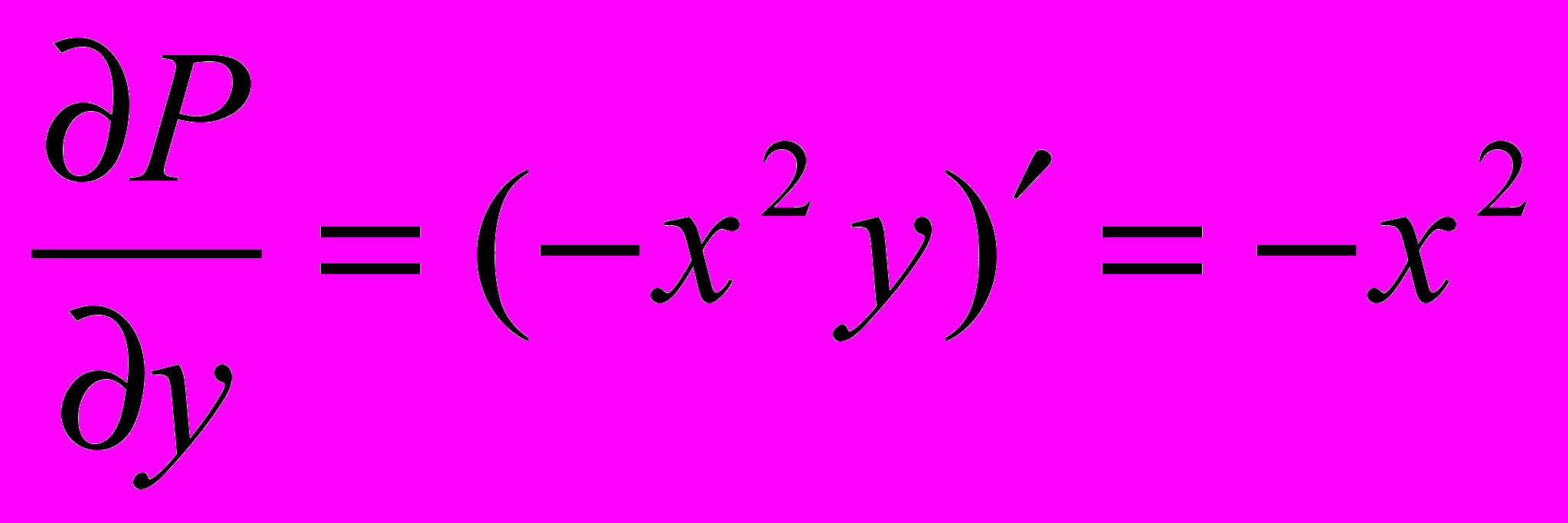

;

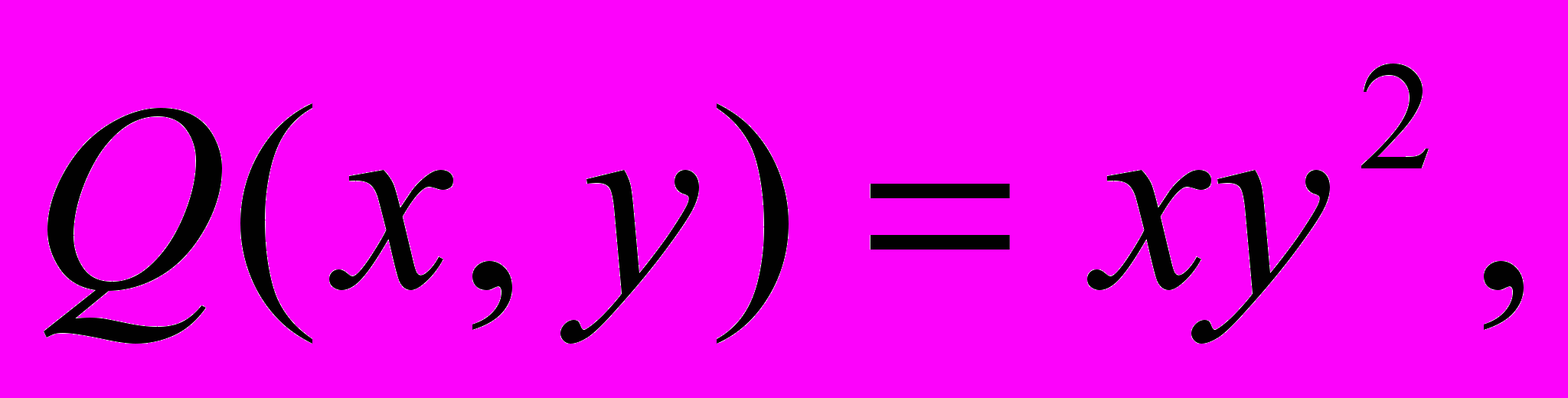тогда:

;

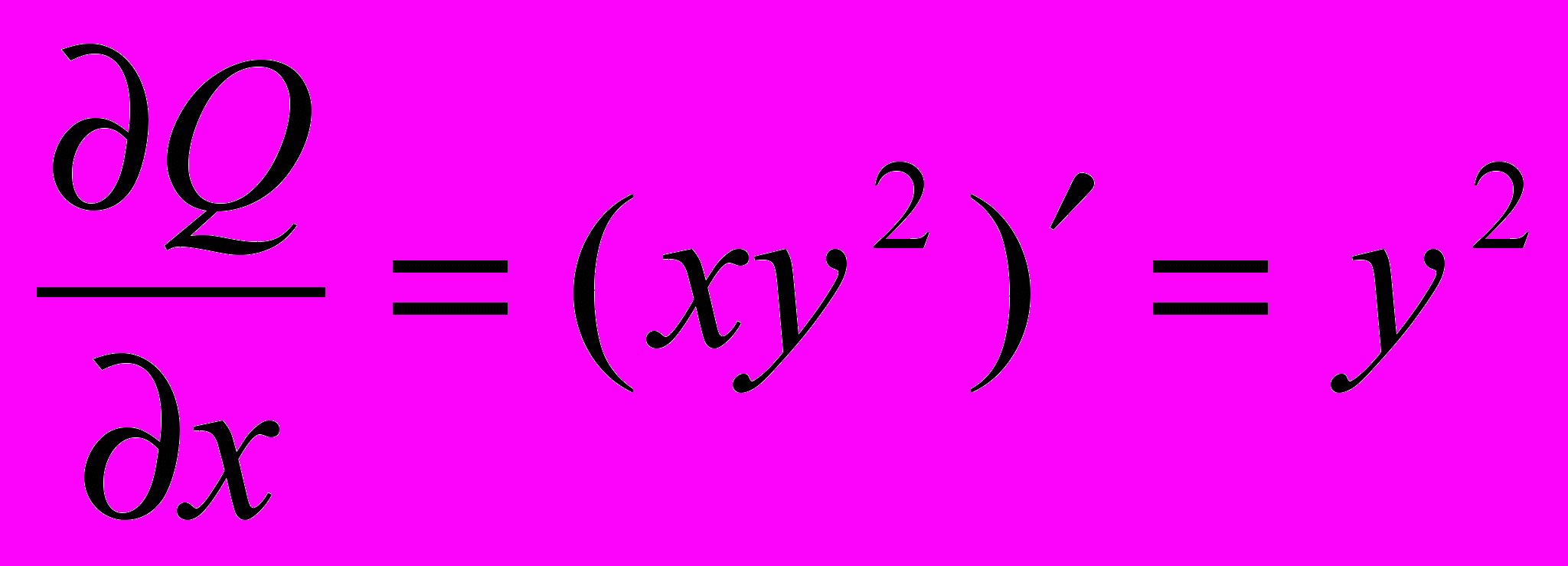применяя формулу Грина получим:



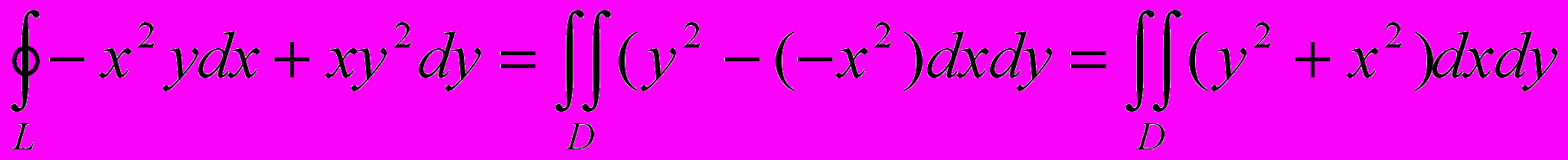
Полученный интеграл удобнее вычислять в полярной системе координат.





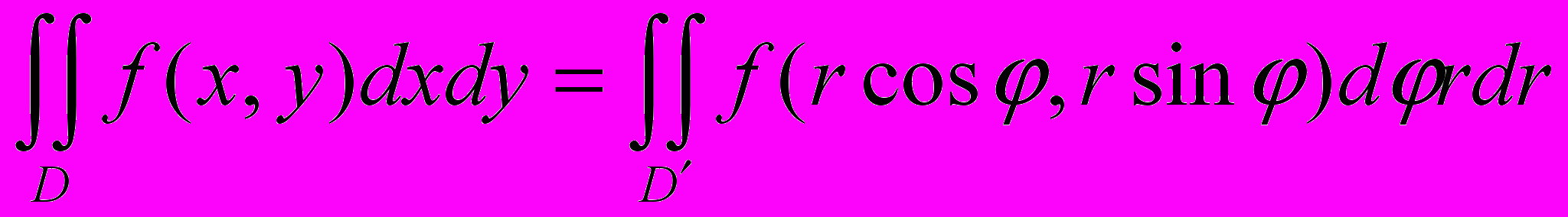
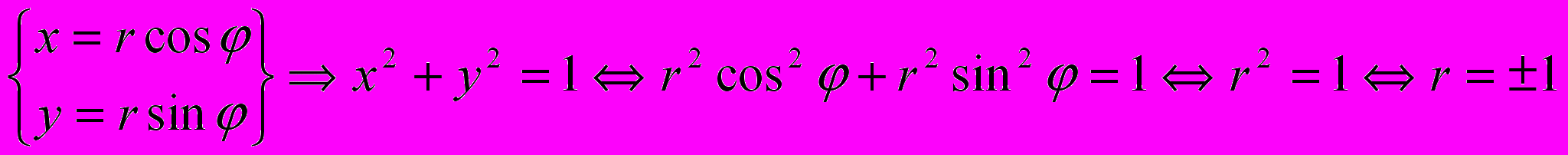
Тогда область 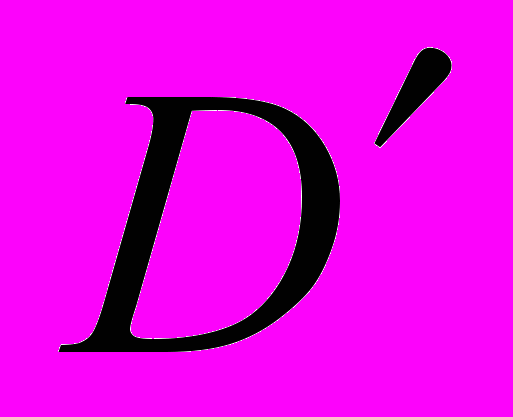будет задаваться неравенствами: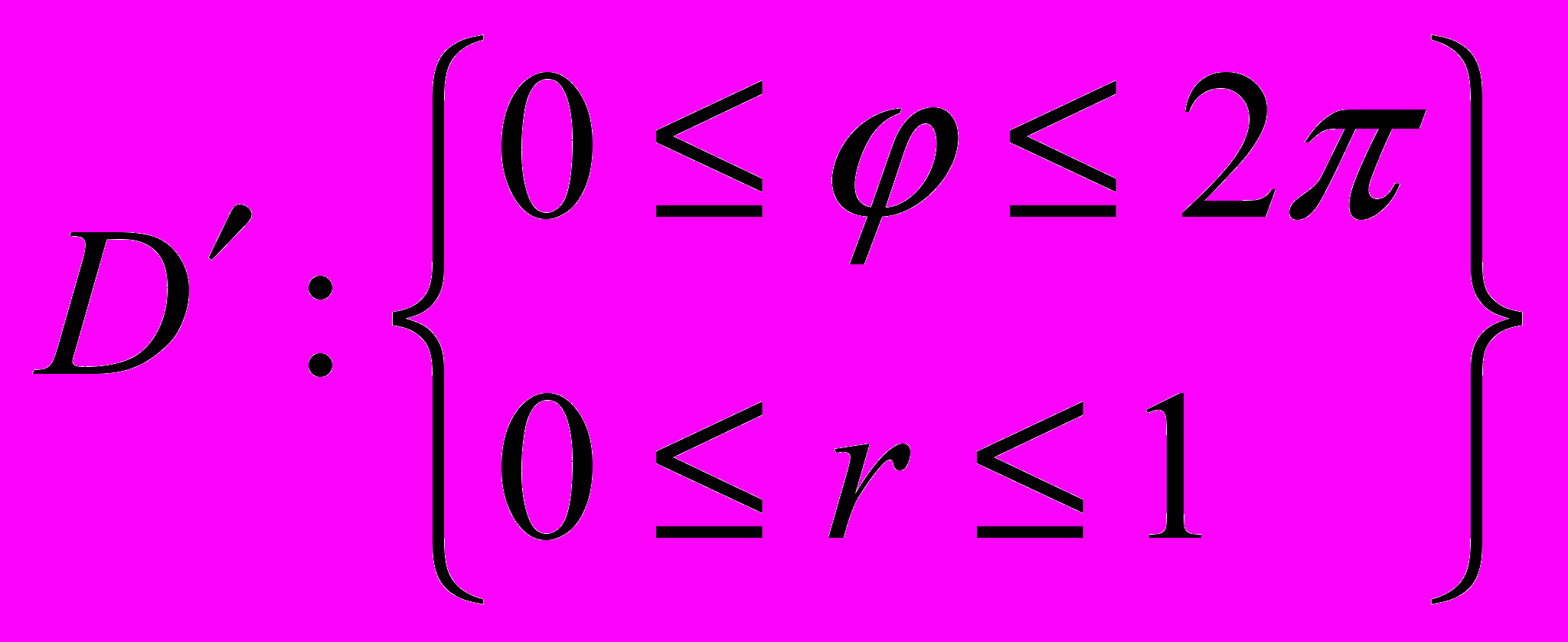



Получим:




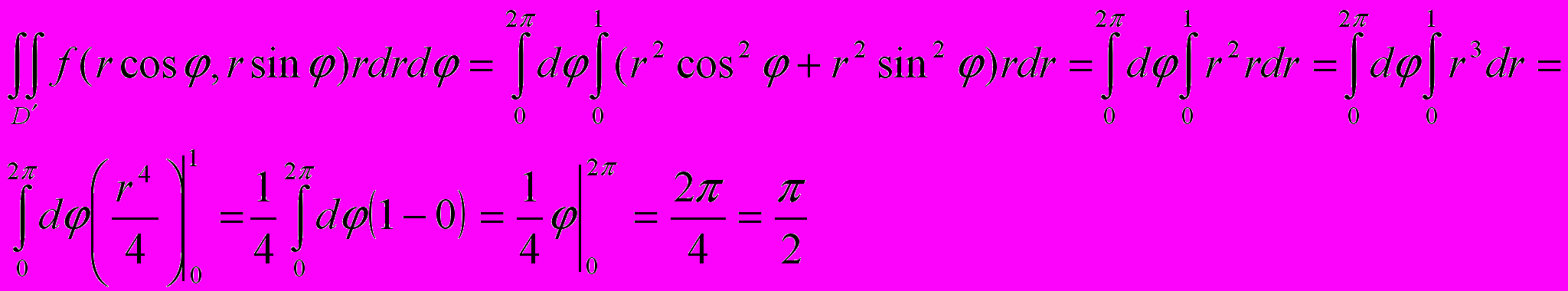
Ответ