Авторефераты по всем темам  >>  Авторефераты по экономике

Моделирование и оптимизация инновационно-инвестиционных процессов

Автореферат докторской диссертации по экономике

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

 

Матвеев Роман Иванович

Моделирование и оптимизация

инновационно-инвестиционных процессов

08.00.13 - Математические и инструментальные методы экономики

Автореферат

диссертации на соискание ученой степени

доктора экономических наук

Кисловодск - 2011

Диссертация выполнена в НОУ ВПО Кисловодский институт экономики

и права

Научный консультант:аа доктор экономических наук, профессор

Курдюков Сергей Иванович

Официальные оппоненты:	доктор экономических наук, профессор Арженовский Сергей Валентинович доктор физико-математических наук, профессор Наталуха Игорь Анатольевич доктор экономических наук, профессор Попова Елена Витальевна
Ведущая организация:	ГОУ ВПО Ставропольский государственный университет

Защита состоится 9 июля 2011 года в 10 часов на заседании объединенного диссертационного совета ДМ 521.002.01 по экономическим наукам при НОУ ВПО Кисловодский институт экономики и права (357700, г. Кисловодск, ул. Р. Люксембург, 42).

С диссертацией можно ознакомиться в научной библиотеке НОУ ВПО Кисловодский институт экономики и права

Автореферат разосланаа аиюняа 2011 года

Ученый секретарь

диссертационного совета аа Бостанова А.И.

Общая характеристика работы

Актуальность темы исследования. Активизация инвестиций в производственный капитал и, особенно, в инновации является одной из приоритетных стратегий роста национальной экономики России на современном этапе. Определение условий оптимального инвестирования и характер влияния на них неопределенностей, присущих экономическим процессам, является значимой задачей для экономико-математического моделирования.

Возможности инвестиций в реальный капитал, в отличие от инвестиций на фондовом рынке, редко предоставляется отдельному предприятию в изоляции. Большинство инвестиционных проектов открыты для фирм с конкурирующими инвестиционными интересами. В некоторых случаях у фирм имеются равные возможности осуществления инновационно-инвестиционных проектов. В таких случаях выбор оптимального момента и объема инвестирования становится для компании важнейшим вопросом. Рассмотрение оптимального инвестирования компании с учетом поведения конкурирующих инвесторов и определение стратегии компромиссного поведения являются актуальным направлением расширения традиционного аппарата оценок, основанных только на анализе финансовых потоков субъекта. Моделирование конкуренции в сфере научно-исследовательских разработок представляет интерес с точки зрения анализа технического прогресса, инноваций и экономического роста. Риск инвестирования в производственные проекты связан со случайными колебаниями спроса на выпускаемую продукцию и цен на ресурсы. Помимо этих рисков, в условиях нестабильной экономики важно учитывать неопределенность налоговых условий, в которых будет функционировать предприятие. Решение этих проблем требует разработки адекватных экономико-математических моделей инвестиционных решений в условиях неопределенности и конкуренции при различных состояниях рынка.

Ключевым условием превращения инноваций в действенный фактор модернизации производства и повышения конкурентоспособности продукции является решение проблем отношений интеллектуальной собственности в сфере инновационных разработок, совершенствования госрегулирования инновационных процессов и формирования эффективных механизмов стимулирования разработки инноваций. Компании, успешно разработавшие инновационные продукты или инновационныеа технологии, часто оказываются неспособными присвоить всю прибыль от результатов научно-исследовательских разработок. Одним из основных путей решения этой проблемы является система патентов. Патент является важнейшим объектом интеллектуальной собственности. Система патентов обеспечивает реализацию двуединой цели: во-первых, поощрение изобретательства и изобретателей взять на себя риск и расхонды по открытию новых путей в науке и производстве, что компенсируется временнными монопольными правами патентообладателя на всю принбыль от результатов инновационных разработок. Во-вторых, это способнствует распространению инновационной технонлогии. Система патентной защиты позволяет обществу располагать полной и регулярнной информацией о существе создаваемых изобретений, которые при отсутствии патентов либо держались в секрете, либо вовсе не создавались. Публикуемые данные патентнной статистики говорят о роли отдельных стран в создании новых технологий и их позиции в международной передаче технонлогий. Тем не менее, злоупотребление монопольной занщитой, которую дает патент, может привести к искусстнвенному созданию препятствий для распространения инноваций.

В частности, анализ оптимальных условий патента на изобретение (оптимального срока действия патента, форвардной и лаггированной защиты патента) должен основываться на достаточно представительной модели конкуренции научно-исследовательских фирм.

Надежные результаты, касающиеся построения оптимальных стратегий реализации инновационно-инвестиционных проектов при наличии упомянутых выше факторов и оптимизации антимонопольной и патентной политики с учетом кумулятивного характера инновационного процесса, могут быть получены в рамках строгих экономико-математических моделейа инвестиционных процессов в производственном и научно-исследовательском секторах в стохастических условиях при наличии межфирменнойа конкуренции, что и обуславливает актуальность проведенных исследований.

Степень разработанности проблемы. Исследованию экономической сущности и классификации корпоративных инвестиций, анализу сущности и задачам управления инвестициями и инвестиционной политике предприятия, вопросам планирования и прогнозирования объемов и структуры инвестиционных ресурсов, управлению их формированием, а также методикам оценки инвестиционного климата посвящены труды отечественных ученых: Р.С.Александрова, А.И.Анчишкина, В.В.Бочанова, С.В.Картышева, В.В.Ковалева, Б.А.Колтынюка, И.И.Мазура, Я.С.Мелкумова, В.М.Павлюченко, А.В.Постникова, В.П.Семенова, Р.А.Фатхутдинова, В.Д.Шапиро, В.В.Шеремета, Е.Г.Ясина, П.Л.Виленского, Н.В.Игошина, Л.Л.Игониной, А.В.Идрисова, М.И.Кныша, Б.А.Колтынюка, А.А.Конопляника, В.П.Красовского, В.Н.Лившица, В.Д.Миловидова, И.В.Сергеева, В.М.Серова, М.А.Субботина и др., а также зарубежных ученых: Д.Аакера, И.Ансоффа, Г.Бирмана, Ю.Бригхэма, Р.Дамари, Э.Джонса, К.Друри, Т.Коллера, Ч.Ли, М.Миллера, Ж.Перара, Р.Оуэна, Б.Санто, С.Шмидта и др.

Управлению инвестициями в инновации и в физический капитал, требованиям к разработке видам инвестиционных проектов, определению стоимости инвестиционного проекта и обоснованию схем его финансирования, оценке эффективности корпоративных инвестиций и управлению реализацией инвестиционных проектов посвящены труды В.М.Аньшина, В.Г.Белолипецкого, Г.Бирмана, Ю.Блеха, В.В.Бочарова, Р.Брейли, П.Л.Виленского, В.А.Воронцова, Д.Ван Хорна, Дж.Ваховича, Х.Виссемы, У.Гетце, Л.Гитмана, В.Н.Глазунова, М.Джонка, Л.В.Ивиной, В.А.Кардаша, А.Д.Касатова, В.В.Ковалева, Л.Крушвица, И.В.Липсица, С. Майерса, Н.Н.Матиенко, Д.Норткотта, Г.А.Панферова, С.Росса, П.Самуэльсона, Д.Сигела, А.Л.Смирнова, Е.С.Стояновой, А.А.Татуева, Т.В.Тепловой, Н.Х.Токаева, В.К.Фальцмана, Дж.Хэмптона, Г.Н.Хубаева, Е.М.Четыркина, Д.Шима, В.И.Якимца и др.

Экономической сущности и оценке рисков реальных инновационно-инвестиционных проектов, методам обоснования управленческих решений в условиях риска и неопределенности посвящены работы А.Абеля, Л.Альвареса, В.И.Аркина, С.В.Арженовского, И.Т.Балабанова, Г.Бирмана, В.М.Гранатурова, А.В.Грачева, М.В.Грачевой, П.Г.Грабового, А.М.Дуброва, Д.Зигеля, В.А.Кардаша, В.Ю.Катасонова, В.Н.Кочеткова, Л.Крушвица, М.Г.Лапусты, О.И.Ларичева, Р.Макдональда, И.А.Наталухи, В.А.Перепелицы, Р.С.Пиндайка, Е.В.Поповой, А.Ф.Рогачева, К.Рэдхэда, А.Д.Сластникова, В.Л.Тамбовцева, Е.Л.Торопцева, Л.Тригеоргиса, Д.Ферера, Н.В.Хохлова, Е.Ю.Хрусталева, Г.Н.Хубаева, С.Хьюса, С.Шмидта и др.

Широкий круг теоретических и практических проблем повышения эффективности производства в результате осуществления инновационной деятельности исследован в трудах А.И.Абалкина, А.И.Анчишкина, Л.С.Бляхмана, Т.Г.Бунича, Л.М.Гатовского, С.Ю.Глазьева, Н.Д.Кондратьева, Д.С.Львова, В.И.Маевского, Е.С.Майминаса, В.К.Фальцмана, А.Ю.Юданова, Ю.В.Яковца и др., а также зарубежных ученых Р.Акоффа, В.Беренса, С.Брю, П.Дасгупты, Э.Кларка, У.Нордхауса, Р.Фостера, К.Фримена, Й.Шумпетера, К.Эрроу и др. Экономическому содержанию инновационной деятельности и проблемам отношений собственности в сфере инноваций посвящены работы Богданова А.И., О.Водачковой, А.Вольского, Г.М.Гроссмана, В.В.Зубчанинова, Р.И.Капелюшникова, Д.И.Кокурина, Н.В.Чайковской, М.Мэлоуна, Т.Сакайя, Б.Санто, Б.Твисса, Э. Хэлпмена, Л.Эдвинсона и др.

Вместе с тем, недостаточно исследованы вопросы моделирования и оптимизацииа инновационно-инвестиционных процессов в условиях стохастических изменений характеристик рыночной и инвестиционной среды при наличии неопределенности, связанной с поведением компаний-конкурентов, которые имеют возможность реализации аналогичных инвестиционных проектов. Практически не изучены проблемы оптимизации патентной и антимонопольной политики в инновационной сфере с учетом кумулятивного характера процесса инновационных разработок. Решение этих проблем требует разработки адекватных экономико-математических моделей инвестиционной и инновационной деятельности в условиях неопределенности и конкуренции, что и определило тему и постановку задач диссертации.

Объект и предмет исследования. Объектом исследования являются производственные предприятия и научно-исследовательские организации. Предметом исследования являются процессы инвестиционной и инновационной деятельности.

Цель и задачи исследования. Цель работы состоит в развитии теории инвестиционных и инновационных процессов в стохастических условиях с учетом конкуренции. Для достижения поставленной цели поставлены и решены следующие задачи:

• разработка и анализ экономико-математической модели инвестицийа в инновационные технологии в условиях различных видов рыночной конкуренции и случайных колебаний инвестиционной среды;
• выявление характеристик равновесных инновационно-инвестиционных стратегий конкурирующих компаний и разработка эффективной реализацииа инвестиционногоа процесса в роли лидера и последователя;
• расчет оптимального времени осуществления корпоративных инвестиций в инновационные технологии и оценка целесообразности модернизации и реструктуризации производственных активов в нестабильных условиях;
• разработка модели инвестиционного процесса в условиях дифференцированной олигополии, анализ равновесных стратегий реализации инновационного процессаа и исследование условий и последствий реализации каждого из видов равновесия в зависимости от микро- и макроэкономических условий;
• выявление влияния инвестиционных процессов в условиях стратегических взаимодействий хозяйствующих субъектов на национальное благосостояние;
• оптимизация динамических траекторий инновационного развития конкурирующих производств на основе теоретико-игровой модели вхождения компании в рынок инновационных разработок в условиях дифференцированной олигополии конкуренции;
• разработка методов прогнозирования лидерства на рынках инноваций в зависимости от случайных колебаний прибыли компаний и стохастических параметров инвестиционной среды;
• качественный и количественный анализ влияния неопределенности инвестиционной налоговой политики на оптимальный инвестиционный процесс в зависимости от характеристик производственной технологии и товарного рынка;
• разработка и анализ стохастической модели олигополистическойа конкуренции в инновационной сфере за получение патента и оптимизация на ее основе срока действия патента;
• оценка эффективности корпоративных объединений патентообладателей на последовательные изобретения и целесообразности проведения государственной антимонопольной политики в сфере инновационных разработок.аа

Теоретическая и эмпирическая база исследования. Теоретической основой диссертационного исследования являются следующие разделы экономической теории: теория инвестиционного процесса и инновационной деятельности, теория олигополистической конкуренции, теория равновесия. Математический аппарат исследования включает методы экономико-математического моделирования, теорию стохастической оптимизации, теорию игр, теорию стохастических дифференциальных уравнений.

Информационно-документальной базой исследования являются статистические материалы Федеральной службы государственной статистики, законодательные акты Президента, Государственной Думы, Правительства РФ, решения и нормативные акты Министерства экономического развития РФа и Федеральной службы по интеллектуальной собственности, патентам и товарным знакам, регулирующие нормативно-правовое обеспечение инвестиционного процесса и инновационной деятельности и осуществление государственной инвестиционно-инновационной политики, федеральные целевые программы развития наукоемких отраслей экономики; материалы научно-практических конференций, публикации отечественных и зарубежных экономистов, тематические Интернет-ресурсы.

Диссертация выполнена в соответствии с п. 1.4 Разработка и исследование моделей и математических методов анализа микроэкономических процессов и систем: отраслей народного хозяйства, фирм и предприятий, домашних хозяйств, рынков, механизмов формирования спроса и потребления, способов количественной оценки предпринимательских рисков и обоснования инвестиционных решений и п. 1.6 Математический анализ и моделирование процессов в финансовом секторе экономики, развитие методов финансовой математики и актуарных расчетов паспорта специальности 08.00.13 - Математические и инструментальные методы экономики.

Научная новизна работы заключается в разработке широкого класса экономико-математических моделей корпоративных инвестиционных процессов и инновационной деятельности в стохастических условиях. Получены следующие основные результаты:

• разработана экономико-математическая модель инвестицийа в создание и внедрение в производственный процесс инновационных технологий, учитывающая различные структуры рыночной конкуренции (дуополистической, олигополистической и монополистической), случайныеа колебания инвестиционных затрат и параметров спроса на товарных рынках, а также неопределенность инвестиционной политики, позволяющая выявлять оптимальные инвестиционные стратегии компаний и устанавливать области параметров, в которых инвестирование не целесообразно;
• построены и проанализированы, методами теории стохастических дифференциальных игр, равновесные инновационно-инвестиционные стратегии конкурирующих компаний (ожидаемая прибыль от внедрения и использования инновационных технологий, оптимальное время и оптимальная динамическая траектория осуществления капиталовложений), что позволяет фирмам-конкурентам разрабатывать эффективную стратегическую реализациюа инвестиционногоа процесса в роли лидера, последователя, или осуществлять одновременное инвестирование;
• рассчитаны, в аналитическом виде, в зависимости от волатильности рыночной среды оптимальное ожидаемое время осуществления инвестиций компании в инновационные технологии и вероятность, с которой инвестиционный порог начала реализации инвестиционного процесса достигается в пределах временного интервала заданной длины, что позволяет оценивать целесообразность модернизации и реструктуризации производственных активов в нестабильных условиях;
• предложено обобщение модели инвестиционного процесса на конкуренцию в условиях дифференцированной олигополии, когда существенное значение имеет различие затрат между конкурирующими компаниями на осуществление капиталовложений, и доказано существование трех типов равновесных стратегий реализации инновационного процессаа (доминантной стратегии, стратегии последователя и одновременной стратегии), что позволило выявить условия и последствия реализации каждого из видов равновесия и преимущества компании-лидера в зависимости от степени дифференциации инвестиционных затрат компаний и таких макро- и микропараметров рыночной среды, как волатильность, динамика спроса и краткосрочная процентная ставка в экономике;
• выявлены качественные и количественные особенности воздействия реализации инвестиционных процессов в условиях стратегических взаимодействий конкурирующих хозяйствующих субъектов на национальное благосостояние, что позволяет оценивать целесообразность осуществления государственной инвестиционной политики, воздействующей на доступ фирм к новым рыночным сегментам и инновационным технологиям;
• установлено существование порогового значения инвестиционных затрат, ниже которого национальное благосостояние в конкурентном равновесии в доминантных и последовательных стратегиях всегда превосходит национальное благосостояние, соответствующее равновесию в одновременных стратегиях, что позволяет сделать вывод о том, что равный доступ компаний-конкурентов к инновационной технологии или новому сегменту товарного рынка может оказаться не оптимальным с точки зрения максимизации национального благосостояния;
• разработана стохастическая теоретико-игровая модель вхождения компании в рынок инновационных разработок в условиях олигополистической конкуренции, позволяющая установить, что присутствие постоянных затрат входа в рынок инноваций является источником эффекта гистерезиса в оптимальных динамических траекториях инновационного развития конкурирующих производств, которыйа усиливается при повышении издержек компаний на вхождение в рынок инновационных разработок и неопределенности доходности компаний и ослабевает с ростом коэффициента корреляции доходности конкурирующих фирм;
• выведены, методами стохастической оптимизации, аналитические формулы для медианы интервала времени, в течение которого каждая иза конкурирующих компаний может занимать доминирующую позицию на рынке инновационных разработок, а также для вероятности сохранения доминирующего положения компании на этом рынке в течение конечного интервала времени, что позволяет компаниям оптимизировать стратегии капиталовложения и прогнозировать лидерство на рынках инноваций в зависимости от случайных колебаний прибыли компаний и стохастических параметров инвестиционной среды;
• выявлено, что более высокая рыночная нестабильность приводит к снижению медианных значений продолжительности доминирования компаний, конкурирующих в рамках дифференцированной олигополии, а вероятность того, что компания будет занимать ведущее положение на рынке инновационных разработок на определенном временном отрезке, растет с повышением волатильности прибыли компаний;
• построена динамическая модель оптимальных траекторий реализации инвестиционного процесса в условиях случайных изменений инвестиционной (налоговой) политики, стохастических изменений спроса, цен на выпускаемую продукцию и интенсивности износа физических производственных активов с учетом специфики технологического процесса, что позволило провести качественный и количественный анализ влияния неопределенности инвестиционной налоговой политики на оптимальный инвестиционный процесс в зависимости от параметра, характеризующего интенсивность конкуренции, а также характеристик производственной технологии и товарного рынка;
• разработана стохастическая модель дифференцированной олигополистическойа конкуренции в инновационной сфере за получение патента, на основе которой рассчитан оптимальный с точки зрения максимизации национального благосостояния срок действия патента в зависимости от различия между частным и общественным выигрышами от использовании инновационной разработки в период времени существования патента, постоянных и переменных затрат на осуществление НИР, невозвратных потерь (связанных с монопольным правом автора патента), прибыли компании-инноватора и эффективности инновационной разработки (сокращения удельных производственных затрат при ее использовании);
• предложены модели кумулятивного процесса разработки и внедрения инновационных продуктов и технологий компаниями-инноваторами, позволяющие оценивать эффективность корпоративных объединений патентообладателей на последовательные изобретения и целесообразность проведения государственной антимонопольной политики в инновационной сфере.аа

Практическая значимость исследования. Практическая значимость работы определяется тем, что разработанные в диссертации модели и методы позволяют решать стратегические и тактические задачи управления и стимулирования инновационно-инвестиционной деятельности конкурирующих компаний в условиях микро- и макроэкономической неопределенности. Разработанная модель инвестиционного процессаа в создание и внедрение в производство инновационных технологий позволяет строить оптимальные инвестиционные стратегии компаний и устанавливать области параметров, в которых инвестирование не эффективно. Построенная модель инвестиционного процесса в условиях дифференцированной олигополии, когда существенное значение имеет различие затрат между конкурирующими компаниями на осуществление капиталовложений, позволяет выявлять условия и последствия реализации равновесных инвестиционных стратегий и оценивать целесообразность осуществления государственной инвестиционной политики, стимулирующей доступ фирм к новым рыночным сегментам и инновационным технологиям. Разработанная стохастическая модель вхождения компании в рынок инновационных разработок в условиях олигополистической конкуренции позволяет компаниям оптимизировать стратегии капиталовложения и прогнозировать лидерство на рынках инноваций. Модель конкуренции в инновационной сфере за получение патента позволяет рассчитывать оптимальный с точки зрения национального благосостояния срок действия патента, оценивать эффективность корпоративных объединений патентообладателей на последовательные изобретения и целесообразность проведения государственной антимонопольной политики в инновационной сфере.аа

Апробация и внедрение результатов исследования. Основные положения и результаты диссертационного исследования докладывались автором на Всероссийской научно-практической конференции Механизмы эффективного управления в рыночной экономике (г. Кисловодск, 2004), V Всероссийском симпозиуме по прикладной и промышленной математике (Сочи, 2004, осенняя сессия), VI Всероссийском симпозиуме Математическое моделирование и компьютерные технологии, (г. Кисловодск, 2004), II Всероссийской научно-практической конференции Корпоративное управление в условиях переходной экономики: теория и практика (Ставрополь, 2004), Международном симпозиуме Математическое моделирование и компьютерные технологии (г. Кисловодск, 2005), V Международной конференции Новые технологии в управлении, бизнесе и праве (Невинномысск, 2005), VIII Международной конференции Экономико-организационные проблемы проектирования и применения информационных систем (Ростов-на-Дону, 2005), IV Международной научно-практической конференции Проблемы регионального управления, экономики, права и инновационных процессов в образовании (Таганрог, 2005), VII Всероссийском симпозиуме по прикладной и промышленной математике (г. Йошкар-Ола, 2006, зимняя сессия), Всероссийской научно-практической конференции Экономика современной России (Волгоград, 2006), Всероссийском симпозиуме Математические модели и информационные технологии в экономике (г. Кисловодск, 2007), IV Международной научно-практической конференции Проблемы регионального управления, экономики, права и инновационных процессов в образовании (Таганрог, 2007), IХ Всероссийском симпозиуме по прикладной и промышленной математике (г. Кисловодск, 2008, весенняя сессия), Всероссийской научной конференции Актуальные проблемы социально-экономического развития (г. Кисловодск, 2009), VI Международной научно-практической конференции Экономическое прогнозирование: модели и методы (Воронеж, 2010), Всероссийских научных чтениях Математическая экономика и экономическая информатика (г. Кисловодск, 2010), Международной научно-практической конференции Математика и ее приложения. Экономическое прогнозирование: модели и методы (Орел, 2011).

Публикации. Основные результаты исследования отражены в опубликованных автором 42 печатных работах общим объемом 35,3 п.л., в том числе 33,65 п.л. - лично автора, включая 2 монографии и 10 работ в изданиях, рекомендованных ВАК для публикаций основных результатов докторской диссертации.

Объем и структура работы. Диссертация состоит из введения, шести глав, заключения и списка использованной литературы.

ОСНОВНЫЕ НАУЧНЫЕ ПОЛОЖЕНИЯ, РЕЗУЛЬтаты И ВЫВОДы

Во введении обоснована актуальность темы исследования, дана характеристика степени изученности проблемы, сформулированы цель и задачи исследования, научная новизна и практическая значимость.

В первой главе Моделирование инвестиционных и инновационных процессов в стохастических условиях рассматриваются экономическая сущность и классификация инвестиций предприятия, формы реальных инвестиций и особенности финансового управления ими, а также виды инвестиционных проектов и требования к их разработке. Рассмотрены методы определения стоимости инвестиционного проекта и обоснования схемы его финансирования. Дается характеристика методов оценки эффективности реальных инвестиционных проектов. Обсуждаются соотношения относительных измерителей финансовой эффективности, проводится сравнение результатов оценки эффективности. Рассматриваются подходы к анализу инвестиционных проектов в условияха риска и неопределенности и особенности принятия решения по инвестиционному проекту в условиях неопределенности. Кратко излагаются основные принципы теории реальных опционов и их отличие от классических методов анализа эффективности инвестиций. Сделан обзор работ, посвященных исследованию экономических аспектов содержания инновационной деятельности, вопросам реализации отношений собственности в инновационной сфере, дается характеристика патента как объекта интеллектуальной собственности. Обсуждаются проблемы совершенствованияа госрегулирования инновационной деятельности.

Во второй главе диссертации Моделирование процессов инвестирования в создание и внедрение инновационных технологий построена непрерывная по времени модель инвестирования, в которой фирма принимает решение о замене существующих производственных активов новыми, более эффективными. Для того, чтобы исследовать влияние стратегических взаимодействий между фирмами, функционирующими в условиях несовершенной конкуренции и неопределенности, предложена модель рынка как дуополии Курно со стохастическим параметром спроса. Обратная линейная функция спроса имеет вид , где аесть мера объема спроса, а а- количество продукции, поставляемой на рынок. Для каждого момента времени апредставляет собой цену товара (услуги), предлагаемого компанией, и может интерпретироваться как мгновенный денежный поток в расчете на единицу проданной продукции. Прибыли фирм описываются геометрическим броуновским движением

, аа а(1)

где а- мгновенная тенденция (тренд стохастического винеровского процесса (1)), а- мгновенное среднее квадратическое отклонение (волатильность), а- приращение винеровского процесса.

Первоначальные постоянные предельные издержки производства единицы продукции составляют , а внедрение новой технологии снижает эти издержки до . Для того, чтобы начать использовать новые производственные мощности, фирма адолжна понести невозвратные затраты . Мгновенные прибыли компании , (соперничающая фирма обозначается ) определяются следующим образом

ааа (2)

Верхний индекс ав выражениях для обозначает фирму, которая произвела замену (не произвела замену) существующих производственных мощностей (индекс обозначает рассматриваемую фирму, а а- конкурирующую фирму). Из соотношений (2) нетрудно установить, что выполняется цепочка неравенства .

Существуют три возможности осуществления компанией аинвестирования относительно решения конкурента (компании ). Во-первых, фирма может инвестировать раньше компании аи, тем самым, стать лидером. Напротив, фирма аможет инвестировать раньше компании , и фирма астановится последователем. Наконец, обе компании могут инвестировать одновременно. Начнем с определения оптимальной стратегии компании-последователя. Далее будет проанализировано оптимальное инвестиционное решение компании-лидера. Затем будет обсужден случай, когда инвестирование осуществляется одновременно. Рассмотрим фирму, которая осуществляет замену существующих производственных мощностей второй (фирму-последователя). Поскольку фирма-лидер уже осуществила замену производственных мощностей, решение последователя о замене не испытывает воздействий стратегических взаимодействий (последователь выбирает свой оптимальный порог в условиях, когда роли фирм предопределены). Из (2) получаем, что после замены производственных активов лидером стоимость компании-последователя в момент аосуществления инвестирования компанией-лидерома равна

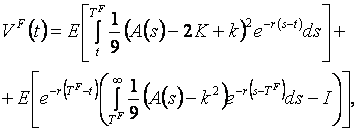а (3)

где а- оператор математического ожидания, а- случайное время остановки, связанное с заменой производственных мощностей последователем. Первое слагаемое в выражении (3) представляет собой ожидаемый дисконтированный денежный поток, получаемый до замены производственных мощностей, В момент апоследователь осуществляет замену и с этого момента производит при более низких предельных издержках . Ожидаемый дисконтированный денежный поток после замены производственных мощностей описывается вторым слагаемым и в (3).

Определены типы равновесия игры двух фирм, сформулированной в рамках теории реальных опционов. Показано, что для фирм оптимально заменять свои производственные мощности последовательно, когда связанные с этим издержки относительно низки, и одновременно в противном случае.

Исследовано влияние волатильности спроса на оптимальный порог инвестирования компанией-последователем в замену производственных активов и оптимальный порог при одновременном инвестировании обеих фирм. Оптимальное пороговое значение, соответствующее инвестированию , может быть выражено следующим образом 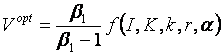, где а- положительный корень уравнения . Проверка показывает, что

так что оптимальные инвестиционные пороги компании-последователя и одновренменного инвестирования возрастают с ростом неопределенности.

Выяснено влияние волатильности на оптимальный инвестиционный порог акомпании-лидера. Оптимальный порог инвестирования компании-лидера равен , где - наименьший корень уравнения . Для выяснения влияние неопределенности рынка на авычислим производную от функции апо , которая может быть представлена в следующем виде

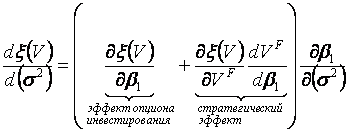а (4)

(а- оптимальное пороговое значение , соответствующее фирме-последователю). Доказано, что имеют место неравенства

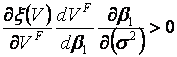, .а а (5)

Анализ показал, что прямой эффект, описываемый первым неравенством (5), доминирует, независимо от значений входных параметров. Доказано, что с ростом неопределенности на товарном рынке барьерное значение спроса, при котором фирма-лидер осуществляет инвестирование в замену производственных мощностей, также возрастает. Из этого утверждения можно заключить, что качественная зависимость порога инвестирования лидера от аподобна зависимости инвестиционного порога от ав нестратегической постановке, т.е. порог инвестирования возрастает с ростом неопределенности (т.е. с ростом ). Причина этого результата состоит в слендующем. Во-первых, в построенной модели учитывается возможность откладывания инвестирования в замену производственных мощностей. Увеличение неопределенности повышает прибыльность замены производственных мощностей лидером (поскольку последователь производит такую замену позже), однако стоимость опциона инвестирования повышается еще больше. Во-вторых, неопренделенность могла бы быть выгодной для более ранней замены производственных мощностей в силу выпуклости функции чистой прибыли. Однако в рассматриваемой модели функция чистой прибыли всегда линейна по стохастической переменной .

Проанализировано влияние неопределенности и стратегических взаимодействий фирм на оптимальный момент инвестирования. Хотя пороговое значение инвестирования имомент инвестирования взаимосвязаны, в общем случае нельзя заключить, что зависимость между этими характеристиками монотонна. Установлено, что ожидаемое время инвестирования компании в замену производственных мощностей растет с ростом неопределенности благодаря двум эффектам:

(6)

Во-первых, для любого данного инвестиционного порога связанное с ним ожидаемое время до момента оптимальной остановки (оптимального момента инвестирования) возрастает с ростом неопределенности (см. первую составляющую правой части в выражении (6)). Во-вторых, для фиксированного уровня неопределенности увеличение оптимального инвестиционного порога приводит к увеличению ожидаемого времени для достижения этого порога (см. вторую составляющую в правой части выражения (6)). Основываясь на анализе неравенства (6), можно заключить, что, когда инвестиционный порог увеличивается благодаря большей неопределенности, ожидаемое время до момента оптимального инвестирования также увеличивается.

Явление гистерезиса наблюдается в случаях, когда равновесное положение экономической системы зависит от траектории

Альтернативный подход для измерения влияния неопределенности на оптимальный момент инвестирования состоит в установлении вероятности, с которой оптимальный инвестиционный порог достигается в пределах временного интервала заданной длины . Знание вероятности оптимальной замены производственных активов в пределах заданного интервала особенно полезно, если этот интервал совпадает с бюджетным периодом. Кумулятивную функцию распределения времени остановки можно записать следующим образом

, (7)

где а- время достижения оптимального порога инвестирования, а а- стандартная функция нормального распределения Лапласа.

Вначале проиллюстрируем соотношение между моментом оптимальной остановки, случайными колебаниями спроса и соответствующими вероятностями для оптимального инвестиционного порога компании-последователя, поскольку этот порог не испытывает влияния стратегических взаимодействий. Далее представим результаты численных расчетов оптимального инвестиционного порога компании-лидера.

Из рис. 1 можно заключить, что форма соотношения между неопределенностью и вероятностью достижения оптимального инвестиционного порога зависит от длины заданного временного интервала. Для достаточно больших временных интервалов вероятность достижения оптимального инвестиционного порога убывает с ростом волатильности. С интуитивной точки зрения этот результат может быть объяснен тем, что плотность распределения вероятностей моментов оптимальной остановки сдвигается вправо (см. (7)), и большие времена достижения уровня спроса, соответствующего оптимальному инвестированию, становятся более вероятными. Кроме того, барьерное значение уровня спроса само возрастает с ростом неопределенности .

При низких значениях авероятность достижения оптимального инвестиционного порога сначала возрастает, а затем убывает. При авероятность достижения инвестиционного порога в определенном интервале времени равна нулю, когда оптимальный момент инвестирования лежит вне этого интервала. Увеличение априводит к разбросу значений плотности распределения

 

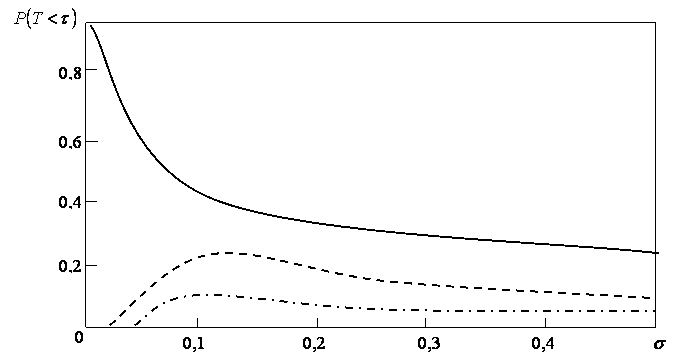
Рис. 1. Кумулятивная вероятность достижения оптимального порога инвестирования компании-последователя как функция неопределенности спроса; , , , , аи . Сплошная кривая - , пунктир - , штрих-пунктир - а(авторская разработка)

 

Рис. 2. Кумулятивная вероятность достижения оптимального порога инвестирования компании-последователя как функция инвестиционного горизонта; , , , , аи . Сплошная кривая - , пунктир - , штрих-пунктир - а(авторская разработка)

вероятностей, так что вероятность достижения порога спроса становится положительной для строго положительных значений . Большийа разброс при увеличении асначала эквивалентен более высокой вероятности достижения оптимального порога инвестирования в замену производственных мощностей. Однако при дальнейшем увеличении волатильности в определенный момент влияние сдвига плотности распределения вероятностей вправо начинает доминировать над эффектом разброса. Вследствие этого кумулятивная вероятность достижения оптимального порога инвестирования вновь уменьшается.

Несмотря на присутствие стратегических эффектов, вероятность замены производственных мощностей компанией-лидером в пределах заданного временного горизонта реагирует на изменения неопределенности и на длину этого интервала аналогично тому, как соответствующая вероятность компании-последователя. При низких уровнях неопределенности авероятность инвестирования возрастает более быстро с ростом длины временного горизонта, чем для высокиха уровней неопределенности. Кроме того, для больших временных горизонтов авероятность замены существующих производственных мощностей всегда убывает с ростом неопределенности, в то время как для более коротких временных горизонтов эта вероятность ведет себя немонотонным образом.

Зависимость между неопределенностью, временем остановки и вероятностями достижения инвестиционного порога лидера иллюстрируетсяа табл. 1.

Таблица 1. Кумулятивная вероятность (в процентах) достижения оптимального порога инвестирования компании-лидера как функция неопределенности спроса для следующего набора параметров:

а

а
0,05	0,06	2,39	24,11	54,32	71,17	80,97
0,10	0,61	5,93	26,79	47,94	59,70	67,24
0,20	0,62	5,14	21,00	36,47	45,10	50,72
0,30	0,46	3,97	16,50	28,66	35,31	39,55
0,40	0,39	3,30	13,57	23,22	28,29	32,39
0,50	0,36	2,93	11,55	19,23	23,02	25,21

Источник: авторская разработка

Определим , акак точку на временной оси, в которой инвестиционный порог адостигается в детерминированном случае. В диссертации доказано утверждение, которое определяет длины временных горизонтов, разделяющих монотонное и немонотонное соотношение между неопределенностью и вероятностью инвестирования. При авероятность достижения инвестиционного порога адо момента авозрастает с ростом неопределенности при относительно низком уровне неопределенности и убывает при достаточно высоком уровне неопределенности, в то время как при авероятность достижения оптимального инвестиционного порога до моментаа авсегда убывает с ростом неопределенности. В табл. 1 параметры выбраны так, что оптимальный момент инвестирования в замену производственных мощностей в детерминированном случае равена . Поэтому соотношение между инвестированием и неопределенностью в столбцах 2-4 немонотонно, в то время как оно монотонно (отрицательно) в столбцах 5-7.

В третьей главе Влияние межфирменной конкуренции на национальное благосостояние аисследованы оптимальные стратегии исполнения опционов инвестирования в условиях несовершенной конкуренции в ситуации, когда инвестиционные затраты различаются между фирмами. Исследование проводилось на основе следующей экономико-математической стохастической модели инвестирования инновационные разработки в условиях дуополистической конкуренции. Две компании, характеризующиеся нейтральным отношением к риску, конкурируют на товарном рынке в условиях неопределенности спроса и несовершенной конкуренции. Неопределенность прибылей фирм описывается геометрическим броуновским движением

,аа (8)

где а- тенденция, а- приращение винеровского случайного процесса. Пусть а- детерминированная мгновенно безрисковая процентная ставка. Неопределенность в функции, описывающей прибыль, входит мультипликативно. Мгновенная прибыль компании авыражается следующим образом ,а где, для

.

Функция аописывает детерминированный вклад в функцию прибыли, причем . Неравенство аозначает, что прибыль компании, инвестирующей первой, превосходит при прочих равных условиях первоначальную прибыль. Кроме того, это инвестирование приводит к относительному снижению прибыли компании, которая к рассматриваемому моменту не осуществила инвестирование в проект, т.е. . Наконец, инвестирование компанией-последователем вдогонку за лидером увеличивает ее прибыль, так что , однако в то же самое время приводит к снижению прибыли лидера, т.е. . Последнее неравенство означает, что между фирмами присутствуют отрицательные экстерналии. Предложенная общая постановка в частных случаях может соответствоватьа дуополии Курно или Штакельберга.

Обозначим инвестиционные затраты компании , ачерез . Без потери общности нормируем инвестиционные затраты так, что а(инвестиционные затраты компании с низким уровнем издержек), а , где . Существуют три типа равновесия, которые могут возникнуть при выборе инвестиционных стратегий, а именно равновесие в доминантных, последовательных и одновременных стратегиях. В диссертации установлены особенности каждого типаа равновесия и представлены условия, при которых возникает каждый из

 

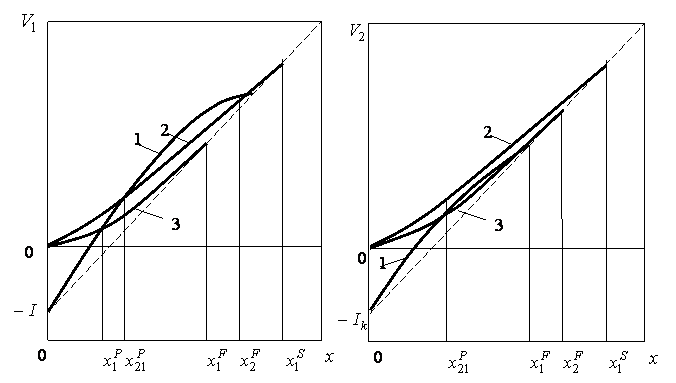
Рис. 3. Капитал компании 1 (рисунок слева) и компании 2 (рисунок справа), если результирующее равновесие есть равновесие в доминантных стратегиях; 1 - фирма в роли лидера, 2 - фирма в роли последователя, 3 - оптимальное одновременное инвестирование, пунктир - одновременное немедленное (не оптимальное) инвестирование (авторская разработка)

 

Рис. 4. Капитал компании 1 (рисунок слева) и компании 2 (рисунок справа), если результирующее равновесие есть равновесие в последовательных стратегиях; 1 - фирма в роли лидера, 2 - фирма в роли последователя, 3 - оптимальное одновременное инвестирование, пунктир - одновременное немедленное (не оптимальное) инвестирование (авторская разработка)

типов равновесия. Равновесие в доминантных стратегиях возникает в ситуации, когда обе компании имеют стимулы стать лидером, т.е. когда невыгодное положение компании 2, связанное с относительно более высокими инвестиционными затратами, относительно невелико. Поэтому фирма 1 должна принимать в расчет то обстоятельство, что фирма 2будет иметь цель опередить фирму 1, как только будет достигнуто определенное пороговое значение опциона инвестирования. Это пороговое значение, обозначаемое апредставляет собой наименьшую реализацию процесса , при которой фирма 2 безразлична между выбором позиции лидера и последователя. Формально аесть наименьшее решение уравненияа , где функция определяется следующим образом агде и аопределяются выражениями (3) и (4) соответнственно. Вследствие этого фирма 1 инвестирует приа агдеа - оптимальный порог инвестирования компании-лидера (компании 1). На первый взгляд может показаться неожиданным, что оптимальный порог инвестирования не зависит от момента инвестирования компании 2. Это объясняется тем, что инвестирование компании 2 в равной степени оказывает влияние на стоимость опциона инвестирования компании 1 ина современное значение стоимости ее проекта после осуществления инвестинрования.

Рис. 3 иллюстрирует выигрыши фирм, соответствующие позициям лидера и последователя, а также одновременному инвестированию на оптимальном одновременном пороге инвестирования компании 1 и немедленному инвестированию обеими фирмами. Фирма 1 инвестирует, как только процесс достигает наименьшей из двух величин: апри которой фирма 2 безразлична между занятием позиции лидера и последователя, и , при которой для компании 1 оптимально инвестировать при условии, что фирма 2 не инвестирует до тех пор, пока не достигается значение . Левая часть рис. 3 иллюстрирует случай, когда а< . Следовательно, в равновесии в доминантных стратегиях выигрыш компании 1 как лидера выше, чем выигрыш, полученный в том случае, если фирма 1 инвестирует второй. Из рис. 3 (правая часть) видно, что слева от аопцион компании 2 быть лидером ниже опциона быть последователем, в то время как вправо от значения аверно противоположное утверждение. Фирма 1 использует тот факт, что фирма 2 не имеет стимулов для инвестирования до , и опережает последнюю на мгновение.

Установлено, что при наличии асимметрии инвестиционных затрат между фирмами фирма 1 извлекает относительный излишек от пребывания в качестве лидера по сравнению с позицией компании-последователя, т.е.

а аа (9)

Равновесие в последовательных стратегиях возникает, если фирма 2 не имеет стимулов стать лидером, т.е. если уравнение ане имеет решений. В этом случае фирма 1 просто максимизирует величину опциона инвестирования, что всегда приводит к инвестированию на оптимальном пороге . Другими словами, фирма 1 ведет себя так, как будто имеет эксклюзивные права инвестировать в выгодный проект, но, конечно, инвестирование компанией 2 все еще влияет на прибыли компании 1.

Рис. 4 иллюстрируют прибыли фирм, соответствующие равновесию в последовательных стратегиях. Из рис. 4 (правая часть) можно сделать вывод, что фирма 2 никогда не выигрывает от занятия позиции лидера по сравнению с позицией последователя. Поэтому фирме 1 нет необходимости принимать в расчет возможность быть опереженной компанией 2. В результате фирма 1 в состоянии инвестировать на своем безусловном пороге а(рис. 4, левая часть). При авеличина опциона инвестирования гладко склеивается с чистым текущим значением приращений выигрыша от осуществления инвестирования. Как и в предыдущем случае, фирма 2 инвестирует на своем пороге последователя .

В диссертации доказано, что существует единственное значение аравное

,аа (10)

которое разделяет области равновесия в последовательных и доминантных стратегиях. При афирма 1 должна принимать в расчет возможное опережение в инвестировании компанией 2, в то время как при акомпании всегда инвестируют последовательно на своих оптимальных поронгах. На интуитивном уровне это утверждение устанавливает существование граничного уровня невыгодного положения компании 2, связанного с относительно более высокими инвестиционными затратами, выше которого фирма 1 может действовать как монополист при исполнении своего инвестиционного опциона.

Другой тип равновесия - равновесие в одновременных стратегиях. В этом случае две компании инвестируют в один и тот же момент времени. В равновесии в одновременных стратегиях одна из фирм должна применить стратегию, которая не оптимизирует ее выигрыш безусловно (заметим, что оптимальные пороги совместного инвестирования различаются). Поскольку оптимальный порог инвестирования компании 1 ниже соответствующего оптимального инвестиционного порога компании 2, единственным вариантом одновременного инвестиционного порога является значение , определяемое выражением 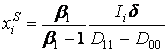. Для осуществления одновременного инвестирования выигрыш компании 1, связанный с ее пребыванием в качестве лидера, должен быть ниже выигрыша, являющегося результатом одновременного инвестирования при . В противном случае фирма 1 будет инвестировать либо при , либо при а(в зависимости от уровня асимметрии инвестиционных затрат между фирмами).

Возникновение конкретного типа равновесия определяется соотношением между относительными выигрышами, которые в свою очередь зависят от уровня асимметрии издержек, преимущества первого хода лидера и таких параметров рынка, как волатильность, скорость роста спроса и краткосрочная процентная ставка. В диссертации доказано, что существует единственное значение , равное

,аа (11)

 

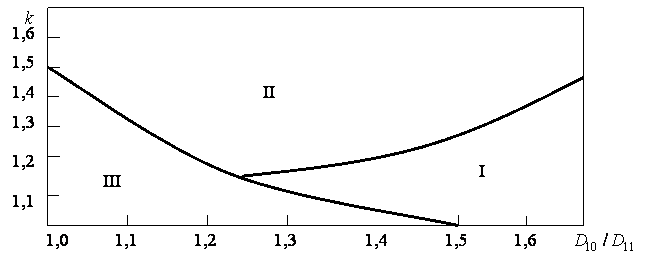
Рис. 5. Области равновесия в доминантных , последовательных аи одновременных астратегиях для следующих значений параметров:

(авторская разработка)

которое определяет области инвестиционного равновесия в одновременных стратегиях и инвестиционного равновесия в последовательных и доминантных стратегиях. При условии арезультирующее равновесие есть равновесие в одновременных стратегиях, а при авозникает равновесие в последовательных и доминантных стратегиях. Это означает, что при относительно высокой степени асимметрии инвестиционных затрат между фирмами (для заданного набора аи ) инвестиционное равновесие в одновременных стратегиях не оптимально, и возникает либо равновесие в последовательных, либо в доминантных стратегиях.

На рис. 5 представлена иллюстрация возникающих типов равновесия. На рис. 5 показаны инвестиционные стратегии как функции преимущества лидера аи асимметрии инвестиционных затрат . Когда асимметрия инвестиционных затрат относительно невелика, и нет существенного преимущества первого хода лидера, компании инвестируют одновременно (треугольная область слева внизу). Когда преимущество первого хода компании-лидера становится существенным, фирма 1 предпочитает позицию лидера одновременному инвестированию. Это приводит к равновесию в доминантных стратегиях (область справа внизу). Наконец, если асимметрия между фирмами значительна (для области значений параметров в верхней части рис. 5), компании инвестируют последовательно, и фирма 1 может действовать как единственный обладатель опциона инвестирования. В диссертации проведены многочисленные численные эксперименты, с целью установления воздействия неопределенности на границы областей существования различных типов равновесия. Эти вычислительные эксперименты показывают, что величина авозрастает, а аубывает с ростом , что означает, что область равновесия в доминантных стратегиях сокращается с ростом . Этот результат свидетельствует о позитивном воздействии неопределенности прибыли фирм на оптимальные инвестиционные пороги фирм и о том, что возрастание неопределенности, определяемой , может приводить к переключению от равновесия в доминантных стратегиях к равновесию, соответствующему оптимальности совместного инвестирования.

Исследовано воздействие степени асимметрии инвестиционных затрат фирм на стоимость каждой из фирм и, в частности, на современную (дисконтированную) стоимость опционов инвестирования фирм. Показано, что при наличии стратегических взаимодействий соотношение между фирмами соотношение между величинойа асимметрии инвестиционных затрат фирм и стоимостью фирм (опционов инвестирования фирм) оказывается в общем случае разрывным и немонотонным.

Чтобы получить лучшее представление о природе немонотонного соотношения между стоимостью компании ааи степенью асимметрии инвестиционных затрат , представима ав виде суммы трех составляющих. Во-первых, вычислим ожидаемую стоимость дисконтированных будущих прибылей в случае, когда инвестирование не осуществляется, что отражает стоимость имеющихся активов . Далее, выведем стоимость собственного опциона инвестирования компании при условии, что другая фирма не инвестирует, . И, наконец, определяется воздействие инвестирования компании-конкурента на прибыли компании, . Сумма ааиа аможет интерпретироваться как стратегическаяа инвестиционной возможности компанииа .

В табл. 2 представлено разложение стоимости компании 1 для различных значений параметра, характеризующего степень асимметрии инвестиционных затрат фирм. Из табл. 1 следует ряд выводов. Во-первых,а нетрудно заметить, что стоимость имеющихся активов не меняется с изменением степени асимметрии инвестиционных затрат. Это естественно, поскольку существующие производственные активы фирм идентичны. Во-вторых, стоимость опциона инвестирования компании 1а растет с ростом параметраа . Это отражает тот факт, что возрастающее конкурентное преимущество компании 1 позволяет фирме 1 удерживать

Таблица 2. Разложение стоимости компании 1 для различных значений параметра, характеризующего степень асимметрии инвестиционных затрат фирм; адля следующих значений параметров:

	1,1	аа 1,15	а 1,2	аа 1,25	1,33	аа 1,5
	57,14	57,14	57,14	57,14	а57,14	57,14
	14,19	15,14	17,16	18,15	18,15	18,15
	- 8,58	- 12,17	- 11,51	- 10,91	- 10,05	- 8,57
а	а 62,75	а 60,12	а 62,80	а 64,39	а 65,24	а66,72
					аа

Источник: авторская разработка

свою инвестиционную стратегию ближе к безусловному оптимумуа а(при котором значениеа ав рассматриваемом примере составляет 18,15). Следовательно, единственным источником немонотонности является взаимодействие инвестиционного решения компании 2 с прибылью компании 1 (см. значения ав табл. 2). Когда параметр, характеризующий степень асимметрии инвестиционных затрат, растет, т.е. когдаа , фирма 1 не имеет более стимулов ждать достижения оптимального порога одновременного инвестирования, и имеет целью опередить фирму 2. Как обсуждалось выше, результирующая игра на опережение приводит к снижению прибылей обоих фирм, и, вследствие этого, их стоимостей.

Для оценки целесообразности применения политики, воздействующей на доступ фирм к новым рыночным сегментам и технологиям, в диссертации исследован вопрос о том, как степень асимметрии инвестиционных затрат влияет на национальное благосостояние. Начнем анализ с вывода выражения для потребительского излишка. Далей обсудим, как инвестиционные стратегии фирм воздействуют на этот излишек. После этого будет представлено и проанализировано соотношение между инвестиционными стратегиями и национальным благосостоянием. Чтобы вывести выражение для потребительского излишка, определим механизм воздействия инвестирования на выгоду потребителя. Рассмотрим простую постановку, согласно которой после инвестирования фирмаа апредлагает товар, имеющий качество , где аобозначает первоначальное (до инвестирования) качество товара.а Поскольку компании предлагают одинаковое качество , они конкурируют в рамках модели Курно, а если фирма 1 инвестирует первой, она получает преимущество Штакельберга на рынке дифференцированного товара. Модель конкуренции Курно восстанавливается после того, как инвестирует фирма 2; тогда обе компании конкурируют на рынке товара одинакового качества.

На рассматриваемом рынке имеется континуум потребителей, характеризующихся мгновенной функцией полезности , где аа- специфический для потребителя параметр, характеризующийся равномерным распределением в интервале , параметр ахарактеризует качество продукции, аа аесть цена продукции в момент . Стохастический параметр , отражающий оценки потребителей, определяется геометрическим броуновским движением

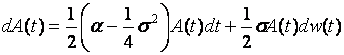,аа (12)

где , ааи аа- параметры и переменные, определенные в (8). Полезно заметить (применяя лемму Ито), что переменную аможно заменить на , посколькуа аточно следует процессу (8).

Если обе компании предлагают продукцию одинакового качества, то мгновенная функция спроса, соответствующая функции полезности , может быть представлена в следующем виде , гдеа аобозначает качество товара, предлагаемое компаниейа ав момента .

Выведем выражения для мгновенного потребительского излишка, обозначаемого , где аиа аотражают качество, предлагаемое фирмами. Чтобы проанализировать полную структуру игры, рассмотрим три случая. В первом случае обеспечивается только качество . Во втором случае одна из фирм обеспечивает качество товара , а другая обеспечивает качествоа , а в третьем случае обе компании предлагают товар качества . В первом и третьем случаяха максимизация мгновенных прибылей фирм, учет национального благосостояния и остаточного излишка даета .

Анализ показывает, что при равновесии в доминантных и последовательных стратегиях потребительский излишек всегда выше, чем при равновесии, соответствующем одновременному инвестированию. Следовательно, с точки зрения потребителей ситуация, когда компании инвестируют одновременно, нежелательна. Нетрудно понять, что, поскольку в этом случае компании оптимально инвестируют позже, товар более высокого качества недоступен потребителям в течение более продолжительного периода. Итак, существует критический уровень инвестиционных затрат, ниже которого национальное благосостояние всегда вышеа в равновесии в доминантных и последовательных стратегиях, чем в равновесии в одновременных стратегиях.

Следовательно, если инвестиционные затраты малы относительно потребительского излишка, наивысший уровень национального благосостояния достигается в равновесии в доминантных стратегиях. В этом случае воздействие на потребительский излишек более ранней поставки товара высокого качества преобладает над потерей стоимости фирм, возникающей в игре в доминирующих стратегиях. Это означает, чтоа в случае относительно низких инвестиционных расходов относительно невыгодное соотношение издержек для одной из фирм-конкурентов приводит к стратегиям, обеспечивающим общественно предпочтительный результат.

Напротив, относительно высокие инвестиционные затраты означают оптимальность одновременного равновесия с точки зрения национального благосостояния. Это объясняется тем, что равновесие в одновременных стратегиях предполагает более позднее возникновение инвестиционных затрат. Поскольку увеличения потребительского излишка, связанногоа с более ранним появлением товара более высокого качества, недостаточно для полной компенсации более высокой современной стоимости раннего инвестирования, откладывание инвестирования выгодно с точки зрения национального благосостояния. Поэтому при наличии высоких невозвратных инвестиционных затрат инвестиционные стратегии, возникающие в одновременном равновесии, максимизируют национальное благосостояние. Это, в свою очередь, означает, что асимметрия инвестиционных затрат фирм нежелательна. Итак, оптимальный с точки зрения максимизации национального благосостояния исход более вероятен, если инвестирование, требующее высоких невозвратных издержек, соответствует низкой асимметрииа инвестиционных затрат фирм, и инвестирование, требующее низких невозвратных издержек, соответствует высокой асимметрииа инвестиционных затрат фирм.

В четвертой главе Моделирование оптимального входа компании в рынок инновационных разработок построена экономико-математическая модель входа в рынок инновационных разработок в условиях, когда компании непосредственно конкурируют за один и тот же рынок, однако могут давать различные и неопределенные прибыли. Рассматривается рынок, достаточно большой только для одной компании (естественной монополии) и две конкурирующие компании аи , которые потенциально способны последовательно монополизировать этот рынок. Каждая фирма имеет свою собственную производственную технологию, и поэтому компании располагают различной операционной доходностью от пребывания на рынке в качестве активной компании. Обозначим через аи ачистый поток операционной доходности, которым располагает каждая из фирм в момент . Для аи азаписываем следующие стохастические дифференциальные уравнения Ито

,аа 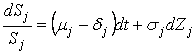,аа (13)

где , , , , аи а- постоянные. Операционная доходность каждой компании неопределенна и подвержена экзогенному шуму , . Возмущения аи амогут быть либо специфическими для компании (например, совершенствование предпринимательских способностей или инновации в производственной технологии компании, сокращающие издержки производства) или воздействовать на всю отрасль (например, неожиданный сдвиг рыночного спроса или изменение предпочтений потребителей). Для учета возможности воздействия общеотраслевых и специфических для компании экономических факторов на прибыль конкурирующих фирм предположим, что соответствующие броуновские движения коррелированны, т.е. , где а- коэффициент корреляции. Предполагается, что если компанииа ааилинаходятся в пассивном состоянии, то они могут войти на рынок ценой постоянных инвестиционныха затрат аи асоответственно.

Предположим, что существует фиктивный центральный планирующий орган, который в любой момент времени может мгновенно делегировать доминирование на рынке наиболее прибыльной из двух фирм. Очевидно, центральный планирующий орган выберет фирму а(фирму ) в качестве активной на рынке, если значения авысоки (низки) и/или значения анизки (высоки). Всякий раз, когда планирующий орган решает сменить доминирующую на рынке фирму, возникают издержки переключенияа аили ав зависимости от направления переключения. Центральный планирующий орган максимизирует свою ожидаемую текущую прибыль, получаемую от рынка за вычетом издержек переключения. Без потери общности можно предположить, что фирма ав данный момент занимает ведущую позицию на рынке и определить акак опцион планирующего органа приостановить деятельность компании ав качестве ведущей и активизировать на рынке фирму . В пространстве состояний фирма аактивна} планирующий орган должен обладать активом возможности переключения доминирующей компании. Доход по этому активу включает: (а) ожидаемый доход от прироста капитала апри изменении стоимости опциона ав зависимости от аи аи (б) дивиденда , потока операционной прибыли от компании , занимающей в настоящий момент времени ведущую позицию на рынке. Полный доход должен быть равен нормальному (требуемому) доходу, т.е. , где а- безрисковая процентная ставка. Применяя лемму Ито для вычисления математического ожидания и учитывая уравнения (13), преобразуем это условие равновесия активов к следующему дифференциальному уравнению второго порядка в частных производных, которому должен удовлетворять опцион

(14)

Установление границ между областями аи аопределяет оптимальную политику переключения для центрального планирующего органа. Оптимальные стратегии переключения аи аопределяются в форме двух независящих от времени значений переменной состояния : верхнего порогового значения и нижнего порогового значения , так что

аесли аактивна, переключение на

аесли аактивна, переключение на .а (15)

Значения аи адолжны быть определены эндогенно посредством условий оптимальности, применяемых на пороговых значениях. Для интерпретации условий (15) предположим, что фирма азанимает в данный момент ведущее положение на рынке и а(обе компании одинаково прибыльны). В такой ситуации планирующему органу безразлично, какая из фирм занимает ведущее положение на рынке, и он может решить активизировать фирму аи прекратить деятельность компании ав качестве ведущей на рынке. Однако, поскольку решение о переключении предполагает постоянные издержки (ав рассматриваемом случае), планирующий орган оптимально отложит это решение до тех пор, пока не будет достигнуто условие, соответствующее ситуации, при которой цена использования опциона авыгоднее рыночной. Другими словами, фирма ане находит оптимальным предпринять инвестирование, пока ее доходность не станет существенно выше доходности компании , так что следует ожидать, что фирма абудет лидировать на рынке еще в течение некоторого периода времени. Если фирма аявляется активной, планирующийа орган будет оптимально ждать, пока ане станет достаточно меньше единицы, так чтобы стало оптимальным вкладывание капитала аи делегирование ведущего положения на рынке фирме . Это разделение порогов оптимальной смены аи аесть проявление гистерезиса. Оптимальная стратегия инвестирования определяется двумя условиями непрерывности решения и двумя условиями гладкого склеивания решений, применяемых на оптимальных границах аи . Определим переменную а(отношение издержек переключения).а Эту переменную можно выразить в виде функции

аа .а (16)

Анализ показывает, что в присутствии неопределенности гистерезис возникает даже при очень малых невозвратных издержках. Этот вывод иллюстрируется рис. 6, на котором показана зависимость оптимальных исполнительных порогов опциона занятия компанией лидирующего положения на рынке от невозвратных издержек для симметричных соперничающих фирм (, , , =). Нетрудно видеть, что интервал между пороговыми значениями исполнения опциона растет с ростом постоянных инвестиционных издержек аи аи уменьшается с ростом коэффициента корреляции доходности соперничающих фирм. Горизонтальная пунктирная линия соответствуета общему пороговому значению исполнения опциона апри отсутствии постоянных инвестиционных издержек. В полном соответствии с интуитивными представлениями, компании проявляют меньшую готовность к занятию ведущего положения на рынке (гистерезис увеличивается) в присутствие более высоких инвестиционных издержек аи .

Далее рассмотрим влияние неопределенности. Нетрудно проверить, что для аимеют место неравенства , , т.е. зона инерции (сохранения на рынке statusquo) расширяется с ростом неопределенности. Однако, даже для экономически идентичных конкурирующих фирм (, , , =) влияние неопределенности на оптимальные пороги занятия компанией лидирующего положения на рынке не симметрично. Для любого уровня корреляции доходности двух соперничающих фирм, как показывает анализ, имеет место соотношение ,т.е. верхняя пороговая граница гистерезиса более чувствительна к изменениям волатильности, чем нижняя пороговая граница.

Анализ показывает, что чем выше волатильность доходностей конкурирующих фирм, тем больше интервал между оптимальными пороговыми

 

Рис. 6. Зависимость инвестиционных порогов аи аот инвестиционных затрат адля отрицательной (пунктирная кривая) и положительной (сплошная кривая) корреляции амежду доходностями фирм при ; . Горизонтальная пунктирная линия соответствует одному пороговому значению при отсутствии постоянных издержек (авторская разработка)

значениями. Корреляция изменений доходностей конкурирующих фирм также оказывает воздействие на оптимальные пороговые значения аи : амонотонно убывает (возрастает) по . Интервал гистерезиса увеличивается с ростом волатильности доходности соперничающих фирм и убывает с ростом коэффициента корреляции между доходностями.а

Для компании-лидера весьма важно знать, как долго продлится ее пребывание на рынке в таком качестве. Кроме того, при фиксированном временном горизонте важно знать, какова вероятность того, что фирма будет лидером на рынке еще в течение определенного времени . Выберем в качестве меры среднего времени пребывания компании ав активном состоянии медиану . Медиана времени пребывания компании ав качестве ведущей определяется решением следующего нелинейного уравнения

а

 

Рис. 7. Зависимость вероятности того, что доминирующая на рынке фирма сменится дважды до момента , от времени апри ; ; ; . При отсутствии входных издержек а(уравнение (18)) и вероятность =0,5 (прямая линия) (авторская разработка)

.а (17)

Медиана времени пребывания компании ав качестве ведущей на рынке увеличивается с ростом постоянных инвестиционных затрат . Медиана времени пребывания компании ав качестве ведущей на рынке убывает с ростом волатильности относительной доходности соперничающих фирм , т.е. чем большей волатильностью характеризуется доходность отрасли, тем меньше период времени, в течение которого ведущая фирма может сохранять свое монопольное положение.а После потери лидирующего положения на рынке фирме важно уметь вычислить вероятность возвращения на рынок в качестве ведущей, т.е. вероятность того, что фирма авновь займет лидирующее положение на рынке после конечного пребывания компании ав качестве ведущей:

 

Рис. 8. Зависимость вероятности того, что фирма Airbus останется лидером сегмента суперавиалайнеров рынка авиалайнеров, от времени при двух возможных ответных стратегиях со стороны компании Boeing: совершенствования существующей модели Boeing-747 (747Х) или создания собственного суперавиалайнера, аналогичного А380. Каждая из соперничающих фирм имеет вероятность 50% быть лидером на рынке через 18,76 лет и 11,18 лет после каждого из альтернативных ответов компании Boeing соответственно. Расчеты проведены по данным Kane, M., Esty, В., 2004. Airbus A3XX: Developing the world's largest commercial jet. WorkingPaper, HarvardBusinessSchool.

а.аа (18)

Очевидно, эта вероятность возрастает со временем. Для экономически симметричных фирм (, , , =) эта вероятность уменьшается с ростом постоянных инвестиционных затрат (см. рис. 6), однако возрастает с ростом волатильности относительной доходности фирм . Заметим, что при а(рис. 7) вероятность (18) превращается в горизонтальную линию 0,5, поскольку в этом случае оба пороговых значения сливаются в одно значение . Нетрудно видеть, что вероятность аочень мала, однако быстро возрастает со временем. Чем выше волатильность аотносительной доходности соперничающих фирм, тем больше вероятность того, что пороговые значения аи абудут достигнуты за меньшее время, что увеличивает вероятность смены ведущей компании на рынке.

Построенная модель применена к анализу данных по сегменту суперавиалайнеров рынка авиастроительной отрасли. Этот рынок представляет собой дуополию двух фирм (Airbus Industrie и Boeing Co.) с длительными периодами доминирования на рынке одной из соперничающих фирм, большими объемами необратимых инвестиций, большой неопределенностью доходности и сильной стратегической конкуренцией. Кроме того, эта отрасль в настоящее время претерпевает большие изменения после решения одной из фирм (Airbus) захватить сегмент суперавиалайнеров рынка авиастроительной отрасли путем крупного инвестирования в проект создания пассажирского лайнера А380. Применение построенной теории позволило выяснить, что оптимальным ответом компании Boeing на проект создания суперавиалайнера А380 компании Airbus является совершенствование существующей модели Боинга-747 как альтернативы более рискованному проекту создания компанией Boeing Co. собственного суперавиалайнера, аналогичного А380 (рис. 10). Установлено, что независимо от ответа компании Boeing Co. может потребоваться 10-20 лет, чтобы вернуть лидерство на рынке суперавиалайнеров.

В пятой главе Экономико-математическая модель инновационного процесса и оптимизация срока действия патента на основе предложенной стохастической модели конкуренции в научно-исследовательском секторе определен оптимальный срок действия патента с точки зрения максимизации национального благосостояния и исследовано влияние оптимального срока действия патента на инвестиции в разработку инноваций.аа

Исследование проводилось на основе следующей модели. В научно-исследовательском секторе предполагается олигополистическое равновесие с постоянными издержками разработки инноваций (открытий) и свободным входом. Компании инновационной отрасли конкурируют за разработку инновации (получение патента), которая затем лицензируется производственным фирмам. Инновация сокращает производственные издержки до уровня . Обозначим через адоход патентообладателя в течение срока действия патента ; а- дальнейшее

 

Рис. 9. Частные и общественные выгоды и ущербы, создаваемые патентом, при нерадикальной инновации (авторская разработка)

 

Рис. 10. Частные и общественные выгоды и ущербы, создаваемые патентом, при радикальной инновации (авторская разработка)

увеличение (если таковое имеет место) национального благосостояния, генерируемое инновацией в течение а(это увеличение благосостояния не присваивается патентообладателем; оно может использоваться потребителями и другими фирмами); а- чистая безвозвратная потеря, связанная с патентом, т.е. потенциальное увеличение национального благосостояния, которое становится доступным обществу только после окончания а(в течение аоно теряется благодаря монопольной власти патентообладателя). , аи апредполагаются стационарными потоками. Функцию спроса обозначаем . Если инновация не является радикальной (инновация считается радикальной, если монопольная цена, связанная с новыми предельными издержками , ниже, чем соответствующая прежним предельным издержкам ) и имеет место идеальная защита патента, так что инновация не может быть имитирована (копирование запатентованной технологии представляет собой создание производственными фирмами на основе информации о конечном продукте, полученном при запатентованной технологии, собственной технологии, как правило, уступающей запатентованной), патентообладатель будет лицензировать новую технологию при плате аза единицу выпуска продукции. Поэтому в постинновационном равновесии выпуск продукции аостанется на доинновационном уровне , и доход патентообладателя будет равен произведению сокращения издержек производства аи доинновационного выпуска. Это площадь ана рис. 9. После того, как азаканчивается, возникает свободный доступ к новой технологии, и уровень выпуска возрастает до , где цена равна новым предельным издержкам. Чистая безвозвратная потеря, создаваемая патентом,а определяется треугольником ана рис. 9. В случае, отраженном на рис. 9, в течение апатентообладатель присваивает полную общественную выгоду от инновации . Рассмотрим теперь случай радикальной инновации. В этом случае патентообладатель лицензирует новую технологию производственным фирмам, взимая платеж,а равный площади ана рис. 10. Основное отличие от случая нерадикальной инновации состоит в том, что в данной ситуации часть увеличения национального благосостояния, которым общество пользуется до того, как заканчивается а, не присваивается патентообладателем. Эта часть соответствует площади ана рис. 10.

Построим модель конкуренции за разработку патентоспособной инновации между анаучно-исследовательскими организациями. В момент акаждая фирма выбирает объем (программу) научно-исследовательских работ аи несет единовременные затраты , где а- предельные затраты на осуществление научно-исследовательской программы. В предположении, что срок разработки инновации компанией араспределен экспоненциально и не зависит от срока получения инновации другими фирмами, вероятность успешного завершения работ компанией ав момент аили до него составляет . Функция выигрыша компании аесть настоящая стоимость ожидаемых доходов за вычетом затрат на осуществление научно-исследовательского проекта, т.е.

, (19)

где а- процентная ставка, а- настоящая стоимость доходов, полученных компанией-инноватором, а- постоянные издержки научно-исследовательских работ, а- переменные издержки научно-исследовательских работ. Максимизация ожидаемых прибылей (19) определяет равновесное количество фирм

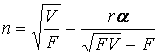.а аа(20)

Видно, что равновесное количество фирм в отрасли является убывающей функцией постоянных издержек научно-исследовательских работ . При анаучно-исследовательский сектор становится совершенно конкурентным. Совокупное инвестирование в научно-исследовательские разработки составляет

, а(21)а

где обозначает часть полных дисконтированных доходов , получаемую патентообладателем. Государство выбирает продолжительность , которая максимизирует национальное благосостояние, являющееся суммой излишка потребителя и доходов научно-исследовательского сектора за вычетом издержек разработки инноваций. Нормируя к нулю поток национального благосостояния до инновации, получаем ожидаемое дисконтированное национальное благосостояние в следующем виде

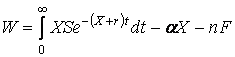, аа(22)

где а- общественная стоимость инновации, т.е. апредставляет собой полную дисконтированную общественную выгоду от новой технологии, которая равна адо истечения аи апосле истечения . Условие существования национального оптимума имеет вид

. (23)

Первый член в левой части уравнения (23) представляет собой непосредственное влияние изменения ана национальное благосостояние. При увеличении аобщество может присваивать все меньшую часть потенциальной дисконтированной выгоды . Другими словами, с ростом аобщество должно ждать дольше, чтобы присвоить треугольник благосостояния . Более того, поскольку прибыли научно-исследовательского сектора снижаются, частное вознаграждение инноватора сокращается (этот эффект усиливается с ростом ). Очевидно, что непосредственное влияние роста ана национальное благосостояние всегда строго отрицательно при условии , при аэто влияние исчезает. Оно является мерой предельных общественных издержек аболее продолжительного срока действия патента . Второй член в левой части уравнения (23) представляет собой неявное влияние ана апосредством аи определяет предельную общественную выгоду ав зависимости от . Чистая предельная общественная выгода от большей продолжительности действия патента пропорциональна сумме трех компонент: , части аот аи . Причина того, что только часть аот аи авлияет на предельную общественную выгоду, состоит в следующем: апредставляет собой компенсацию благодаря изменению издержек научно-исследовательских разработок (согласно условию нулевой прибыли), а аесть потеря, связанная с монопольным владением патента. Поскольку

,аа а(24)

предельная общественная выгода от увеличения срока действия патента авсегда положительна. Оптимальный срок действия патентаа аопределяется единственным решением условия первого порядка

, (25)

Доказано, что если оптимальный срок аконечен, то он: (1) растет по ; (2) возрастает по ; (3) возрастает по ; (снижается с ростом по , если ; (5)а снижается с ростом .Причина того, что растет с увеличением , ясна, т.к. аесть собой общественная выгода от инновации, которая не присваивается собственником патента и вследствие этого представляет собой положительный внешний эффект инновационной деятельности. Воздействие ана асложнее. Во-первых, рост авызывает уменьшение , и это снижает предельные общественные затраты, связанные с ростом . Во-вторых, динамика аоказывает влияние на : и , и аснижаются по , но их частное не меняется при изменении а, так что ане зависит от . Ростадолжен приводить к росту аи, следовательно, к повышениюа . При снижении аинвестиции в разработку инновацийа аувеличиваются, и это позволяет обществу снизить . Оптимальный срок легитимности патента убывает по аи . По смыслу аочевидно, что этот параметр негативно влияет на оптимальную продолжительность действия патента, поскольку аявляется мерой общественных издержек патентной защиты. Более высокие значения аусиливают частные стимулы для осуществления инноваций, и также делают инвестиции в научно-исследовательские разработки более целесообразными с точки зрения национального благосостояния. Как оказывается, аувеличивается существеннее, чем желательно с точки зрения национального благосостояния, так что регулирующие экономическую политику институты реагируют на это снижением продолжительности действия патента.

В диссертации установлено, что если инновация не является радикальной, убывает с ростом эффективности инновации , и становится бесконечным при достаточно малых инновациях (, аточно определено в диссертации). Этот результат дает ответ на вопрос о том, должны ли большие инновации быть защищены сильнее малых. Малые инновации должны быть защищены в течение более длительного периода по двум причинам: во-первых, большие инновации связаны с большими чистыми безвозвратными потерями, во-вторых, малые инновации требуют большей продолжительности действия патента, чтобы убедить компании инновационной отрасли инвестировать в исследования. Очевидно, очень малые инновации (соответствующие условию ) не способствуют стимулированию инвестиций в разработку инноваций и поэтому не требуют защиты. С ростом аоптимальный срок действия патента ауменьшается, если инновация не является радикальной. Возникает вопрос, как изменится ситуация, если инновация становится радикальной. Для радикальных инноваций аположительно. Более того, поскольку кривая предельного дохода наклонена вниз, авозрастает с ростом величины инновации. На основании этого в ряде работ делается вывод о том, что абольше для радикальных инноваций. Анализ, проведенный в работе, показывает, что это не обязательно верно, поскольку апродолжает возрастать с ростом величины инновации даже когда инновация радикальная, и это же может быть верно в отношении ; эти компенсирующие эффекты могут перевесить эффект положительности и возрастания .

Далее в диссертации на основе предложенной модели инновационного процесса как движения компании-лидера вверх по лестнице качества товара (компании, имитирующие инновационную продукцию, могут следовать по лестнице качества за лидером, однако они ограничены условиями патентов) исследуется влияние ана скорость инновационного процесса и на благосостояние потребителей. Найдены сроки действия патента, максимизирующие скорость инновационного процесса и национальное благосостояние, и проанализировано соотношение между ними.

Рассмотрим непрерывную лестницу качества с единственным лидером-инноватором. Предельные издержки создания инновации апредполагаются постоянными. Издержки прохождения расстояния авверх по лестнице качества товара (технологии) составляют . На рынке имеются потенциальные имитаторы, способность которых производить вдоль лестницы качества ограничена по времени сроком действия патента . А именно, если лидер создает инновационную продукцию в момент , потенциальные имитаторы не могут начать производство этой продукции до момента . Предполагаем, что, когда аазаканчивается, издержки копирования равны нулю. Удельные издержки производства продукции (отличающиеся от издержек на создание инновации) вдоль лестницы качества продукции предполагаются постоянными и равными . Пусть апредставляет множество всех товаров, существующим в момент , где аобозначает конкретный товар; аобозначает положение товара ана лестнице качества. Потребительская оценка качества товара апредставляется функцией , . Количество товара , потребляемое в момент , обозначаем . Задача потребителя состоит в выборе количества акаждого товара аиз множества доступных товаров в момент апри условии бюджетного ограничения, т.е.

а,а ,аа (26)

где а- цена товара ав момент , а а- экзогенно задаваемые полные расходы потребителя в течение каждого периода.

Пусть а- положение (на лестнице качества) товара наивысшего качества, существующего в момент , т.е. ; а- положение наиболее продвинутого товара, который может быть имитирован в момент апри данном патентном законе. При условии установления сдерживающих цен цена лидера, производящего только продукцию наивысшего качества, равна а(, );а аздесь и далее относится к цене наиболее продвинутой продукции, доступной в данный момент времени. Наиболее низкая цена, при которой (потенциальный) имитатор будет производить товар в положении , равна , где аесть цена наиболее продвинутой продукции, которая может быть имитирована. Чистый доход (без учета затрат на разработку инновации) компании-лидера в момент апоэтому составляет

.аа а(27)

После разработки инновации патентный закон определяет положение, соответствующее угрозе копирования. Полное описание угрозы копирования дается следующими уравнениямиа , ; , . Эти уравнения означают, что имитатораа не может начать движение по лестнице качества, пока не закончится срок действия патента ана первый продукт компании-лидера в момент . В дальнейшем положение имитатора на лестнице качества в момент асоответствует положению, которое лидер занимал апериодов времени назад (т.е. ). Фирма-лидер максимизирует текущую дисконтированную стоимость потока прибылей, определяемых выражением (27), выбирая положение на лестнице качества в каждый период времени, т.е. лидер максимизирует следующее выражениеа

,аа (28)

где а- дисконтный фактор; асуть предельные издержки на разработку инновации. В диссертации получено следующее прибылемаксимизирующее значение скорости инновационного процесса

.а (29)

Уравнение (29) является определяющим в описании скорости инновационного процесса в построенной модели. Анализ выражения (29) приводит к следующему необходимому условию, обеспечивающему положительную скорость инновационного процесса

.а (30)

В работе получено следующее выражение для благосостояния потребителей в зависимости от

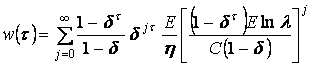.аа а(31)

Установлено, чтоа афункция аимеет максимум,ааи . Проанализировано соотношение между , максимизирующим скорость инновационного процесса , и , максимизирующим благосостояние потребителя . Установлено, что при всех значениях параметров срок действия патента, максимизирующий скорость инновационного процесса, превосходит срок действия патента, максимизирующего благосостояние потребителя.

Различие между сроками действия патента, максимизирующим благосостояние потребителя и скорость инновационного процесса, создает проблему выбора срока действия патента. Если, в соответствии с Патентным законом РФ, срок действия патента выбирать из условия из условия обеспечения ускорения технического прогресса, благосостояние потребителя будет субоптимальным.

Построенная модель позволила выявить фундаментальный механизм, ответственный заа существование максимизирующих скорость инновационного процесса и благосостояние потребителей сроков действия патента, который может реализоваться и в более сложных модельных формулировках. А именно, увеличение срока действия патента оказывает противоположное воздействие на величину и частоту инноваций. Более длительный срок патента увеличивает величину, но уменьшает частоту инноваций. Аналогично, срок патента, который максимизирует благосостояние потребителей, уравновешивает влияние величины и частоты инноваций с точки зрения национального благосостояния. Точки равновесия с точки зрения максимизации скорости инновационного процесса и благосостояния потребителей различаются в силу более существенного влияния частоты появления инноваций на благосостояние потребителей. Снижение частоты появления инноваций уменьшает благосостояние потребителей непосредственно через дисконтирование и неявно посредством своего влияния на скорость инновационного процесса. Следовательно, эффекты уменьшения частоты и увеличения величины инноваций уравновешивают друг друга при меньшем сроке действия патента с точки зрения максимизации благосостояния потребителей, чем с точки зрения максимизации скорости инновационного процесса. Построенная модель может быть также применена для исследования различий сроков действия патентов между отраслями.

В шестой главе Модели оптимальной патентной и антимонопольной политики при кумулятивном процессе разработки инноваций анализируется оптимальная степень форвардной патентной защиты в рамках модели конкуренции за разработку инновации и получение патента, состоящей из двух стадий.

Патентная система обеспечивает защиту патента тремя путями. Во-первых, некоторая защита неявно обеспечивается требованием новизны изобретения (патентоспособности). Во-вторых, защита патента обеспечивается границами патента, накладывающими ограничения на продукты (технологии), которые не могут производиться другими фирмами без лицензии патентообладателя. Нижняя граница препятствуета копирования, определяя продукты (технологии) ниже по качеству запатентованных, которые не могут производиться без лицензии. Форвардная граница ограничивает будущих инноваторов, определяя продукты (технологии) более высокого качества, чем запатентованные, которые не могут производиться без лицензии. Отмеченные два инструмента защиты патента - требование новизны изобретения (инновации) и форвардная граница - определяют стимулы кумулятивного инновационного процесса в целом, поскольку определяют распределение прибыли, создаваемой последовательными инновациями. При наличии указанных двух инструментов защиты патента: условия патентоспособности и форвардной границы в принципе существуют четыре режима патентной политики, соответствующих тому, является ли вторая инновация непатентоспособной и нарушающей условия патента на инновацию первого поколения (UI), непатентоспособной и не нарушающей условия патента на первую инновацию (UN), патентоспособной и нарушающей условия патента на первую инновацию (PN) и патентоспособной и не нарушающей условия патента на первую инновацию (PN). Режим UNа может быть исключен из рассмотрения, поскольку в этой ситуации отсутствуют стимулы для инвестирования во вторую инновацию (которая, будучи открытой, становится общедоступной). Если вторая инновация непатентоспособна и нарушает условия патента на первую инновацию, только первый инноватор может на законных основаниях использовать ее, так что только он имеет стимулы для инвестирования в инновацию. Поэтому в режиме UI межвременные экстерналии полностью интернализуются. В режиме PIвторой патент нарушает условия защиты первого, поэтому оба патента являются взаимно блокирующими, и ни один из инноваторов не может использовать вторую инновацию без согласия другого. Это позволяет первому инноватору получить некоторую ренту от второй инновации, даже если она разработана другой компанией. Когда второй патент не нарушает условия первого, первый патентообладатель не имеет прав контроля над второй инновацией, и поэтому в режиме PN первый инноватор не получает ренты от инновации второй стадии. Очевидно, обсуждаемые три режима следующим образом расположены по убыванию степени форвардной защиты: UI обеспечивает наиболее сильную защиту первому инноватору, PN наиболее слабую.

Обозначим через апоток дохода, приобретаемого первым инноватором. Тогда, предполагая для простоты бесконечный срок действия патента, получаем частную стоимость первой инновации в виде , где а- дисконтная ставка. Аналогично, апредставляет собой частную стоимость второй инновации. Считаем, что в начале каждой стадии конкуренции за разработку инноваций акаждая фирма апринимает программу научно-исследовательских работ аи несет единовременные издержки , где а- удельные затраты на разработку инновации на -ом этапе. Исследовательские проекты различных фирм предполагаются независимыми друг от друга, так что совокупная мгновенная вероятность успеха равна сумме индивидуальных вероятностей.

В диссертации доказано, что режим UIвсегда приводит к недоинвестированию во вторую инновацию, поскольку существование конкуренции в научно-исследовательском секторе на первой стадии исследования имеет тенденцию само по себе противодействовать межвременной экстерналии, делая поэтому полную интернализацию субоптимальной. Хотя движение от режима UI к PI или к PN предполагает дискретное, а не предельное изменение в инвестировании в научно-исследовательский сектор и поэтому не должно быть желательным с точки зрения национального благосостояния, имеется возможность увеличения благосостояния. Действительно, одним из результатов этой главы является то, что при симметричных инновациях (т.е. при , аи ) национальное благосостояние максимально в режиме PN и минимально в режиме UI.

Опуская предположение о симметрии инноваций, можно указать три главных фактора, определяющих ранжирование режимов с точки зрения национального благосостояния: отношение не присвоенных стоимостей двух инноваций а(поскольку функция национального благосостояния однородна первой степени по аи , только их отношение аимеет значение); удельные затраты на научно-исследовательские разработки аи а(которые могут рассматриваться как показатели неочевидности инноваций) и прибыльность инноваций аи . Идентифицированы различные факторы, препятствующие сильной форвардной защите патента. Во-первых, при условии свободного входа в научно-исследовательский сектор ожидаемое национальное благосостояние полностью определяется не присвоенной выгодой от инноваций. Следовательно, если не присвоенная выгода от второй инновации велика по сравнению с выгодой от первой инновации, становится общественно выгодным сдвигать стимулы к инвестированию от инновации на первой стадии к инновации на второй стадии путем снижения форвардной защиты патента. Во-вторых, если первая инновация становится более прибыльной, то частные выгоды обеспечивают более сильную мотивацию для инвестирования в первую инновацию; сдвиг рент к инноватору первой стадии становится менее привлекательным. Поэтому, по мере того как прибыльность первой инновации возрастает, следует ожидать, что режим PN будет привлекательнее режима PI, и режим PIпривлекательнее режима UI. Аналогичный аргумент объясняет, почему сильная форвардная защита становится менее желательной, если издержки на получение первой инновации снижаются. Напротив, форвардная защита становится более желательной по мере роста не присвоенной выгоды от первой инновации, увеличения прибыльности второй инновации или снижения издержек для разработки второй инновации. Наконец, если первая и вторая инновации являются субститутами, в режиме PN часть ренты первого периода переходит ко второму инноватору. Поскольку режим PN итак сдвинут в пользу последнего, это делает режим PI относительно более привлекательным.а

Подытожим основные результаты. Во-первых, анализ показывает, что слабая форвардная защита патента желательна во многих случаях. Во-вторых, важно различать присваиваемую и не присваиваемую патентообладателем прибыли от инноваций, поскольку они имеют противоположные применения в патентной политике: меньшая защита требуется высокодоходным инновациям, в то время как сильная защита желательна, когда большая часть прибылей от инновации являются не присваиваемыми. Следовательно, слабая форвардная защита желательна, когда не присваиваемый доход от второй инновации относительно высок, в то время как сильная защита необходима, когда частная прибыль от второй (первой) инновации высока (низка).

оСНОВНЫЕ ПУБЛИКАЦИИ

ПО ТЕМЕ ДИССЕРТАЦИОННОГО ИССЛЕДОВАНИЯ

1. Монографии

1. Матвеев Р.И. Модели конкуренции в инновационной сфере. - М.: МИСОН, 2009. - 7,3 п.л.
2. Матвеев Р.И. Стратегические взаимодействия фирм в стохастических условиях. - М.: МИСОН, 2010. - 7,1 п.л.

2.а Статьи в периодических изданиях, рекомендованных ВАК для публикации основных результатов диссертации на соискание ученой степени доктора наука

1. Матвеев Р.И. Моделирование кумулятивного инновационного процесса и патентной политики // Экономический вестник Ростовского государственного университета. - 2009, № 4. - 0,4 п.л.
2. Матвеев Р.И. Оптимизация инновационно-инвестиционых стратегий в условиях дуополистической конкуренции // Экономический вестник Ростовского государственного университета. - 2009, № 4. - 0,4 п.л.
3. Матвеев Р.И. Моделирование инвестирования в новые технологии в условиях неопределенности и конкуренции // Управление экономическими системами: электронный научный журнал. - 2010. - № 2 (22). URL: - 0,8 п.л.
4. Матвеев Р.И. Моделирование и оптимизация инновационно-инвестиционых стратегий в стохастических условиях // Управление экономическими системами: электронный научный журнал, 2010. - № 2 (22). - 0,8 п.л.
5. Матвеев Р.И. Моделирование и оптимизация срока действия патента  с учетом скорости инновационного процесса  // Управление экономическими системами: электронный научный журнал, 2010. - № 3 (23). - 0,6 п.л.
6. Матвеев Р.И. Моделирование оптимального входа конкурирующих фирм в рынок в стохастических условиях // Управление экономическими системами: электронный научный журнал, 2010. - № 3 (23). - 0,6 п.л.
7. Матвеев Р.И. Анализ влияния изменений экономической политики в отношении инвестиций на инвестиционную стратегию компании // Управление экономическими системами: электронный научный журнал, 2010. - № 4 (24). - 0,6 п.л.
8. Матвеев Р.И. Оптимизация инвестиционного процесса в условиях случайных колебаний спроса и налоговой политики // Бизнес. Образование. Право. Вестник Волгоградского института бизнеса. - 2011. - № 15. - 0,5 п.л.
9. Матвеев Р.И. Оптимальные инвестиционные стратегии фирм и типы равновесия в дуополистической игре // Управление экономическими системами: электронный научный журнал, 2011. - № 3 (24). - 0,6 п.л.
10. Матвеев Р.И. Стратегические взаимодействия фирм в модели асимметричной дуополии и национальное благосостояние // Управление экономическими системами: электронный научный журнал, 2011. - № 4 (25). - 0,7 п.л.

3. Статьи в центральных научных изданиях и в сборниках Международных и Всероссийских конференций

1. Матвеев Р.И. Прогнозирование стратегического лидерства в условиях дуополистической конкуренции // Материалы Всероссийской научно-практической конференции Механизмы эффективного управления в рыночной экономике. - Кисловодск, 2004. - 0,2 п.л.
2. аМатвеев Р.И. Оптимальные инвестиционные стратегии в условиях несовершенной конкуренции с учетом неопределенности спроса // Сборник научных трудов VI Всероссийского симпозиума Математическое моделирование и компьютерные технологии. Секция 2 Математическое моделирование в экономике и других общественных науках. - Кисловодск, 2004. - 0,1 п.л.
3. аМатвеев Р.И. Моделирование инвестирования в инновационные технологии в условиях стратегических взаимодействий компаний // Сборник научных трудов VII Международного симпозиума Математическое моделирование и компьютерные технологии. - Кисловодск, 2005. - 0,25 п.л.
4. аМатвеев Р.И. Моделирование оптимального входа компании в рынок и рыночного лидерства в стохастической дифференциальной игре // Сборник научных трудов VII Международного симпозиума Математическое моделирование и компьютерные технологии. - Кисловодск, 2005. - 0,25 п.л.
5. Матвеев Р.И., Бычкова М.М. Моделирование начала производства на новом рынке в условиях стратегической конкуренции // Современные научные исследования. - 2005, № 1. - 0,4 п.л. (в т.ч. автора 0,2 п.л.).
6. Матвеев Р.И., Тер-Акопов Г.Н. Анализ дуополистической конкуренции с учетом волатильности доходности конкурирующих фирм и оптимальных стратегий рыночного лидерства // Современные научные исследования. - 2005, № 1. - 0,7 п.л. (в т.ч. автора 0,35 п.л.).
7. Матвеев Р.И. Влияние структурных изменений экономической среды на оптимальное инвестирование в стохастических условиях // Современные научные исследования. - 2005, № 2. - 0,7 п.л.
8. Матвеев Р.И. Оптимизация инновационно-инвестиционных стратегий компании в условиях конкуренции // Современные научные исследования. - 2005, № 2. - 0,7 п.л.
9. Матвеев Р.И. Оптимальные инвестиционные стратегии в условиях несовершенной конкуренции с учетом неопределенности спроса // Современные научные исследования. - 2005, № 4. - 0,7 п.л.
10. Матвеев Р.И. Моделирование рыночного лидерства в стохастической дифференциальной игре // Современные научные исследования. - 2006, № 1. - 0,6 п.л.
11. Матвеев Р.И., Чепиков Э.В. Последовательные инновации и антимонопольная политика // Современные научные исследования. - 2006, № 4. - 0,7 п.л. (в т.ч. автора 0,35 п.л.).
12. Матвеев Р.И., Пышкин Н.И. аПатентная и антимонопольная политика при кумулятивном инновационном процессе // Современные научные исследования. - 2006, № 2. - 0,9 п.л. (в т.ч. автора 0,45 п.л.).
13. Матвеев Р.И. Сроки действия патента, оптимизирующие скорость инновационного процесса // Современные научные исследования. - 2006, № 2. - 0,6 п.л.
14. Матвеев Р.И., Бычкова М.М. Моделирование оптимальных стратегий корпоративного инвестирования в инновационные технологии в стохастических условиях // Современные научные исследования. - 2006, № 3. - 0,7 п.л. (в т.ч. автора 0,35 п.л.).
15. Матвеев Р.И. Моделирование оптимального срока действия патента с точки зрения национального благосостояния // Современные научные исследования. - 2006, № 3. - 0,6 п.л.
16. Матвеев Р.И. Конкуренция в инновационной сфере и оптимальный срок действия патента // Современные научные исследования. - 2007, № 1. - 0,8 п.л.
17. Матвеев Р.И. Моделирование рыночного лидерства в стохастических условиях // Сборник научных трудов Всероссийского симпозиума Математические модели и информационные технологии в экономике. - Кисловодск, 2007. Ца Т. 2. - 0,4 п.л.
18. аМатвеев Р.И. Моделирование влияния изменений инвестиционной политики на стратегию компании методами теории реальных опционов // Сборник научных трудов Всероссийского симпозиума Математические модели и информационные технологии в экономике. - Кисловодск, 2007. Ца Т. 2. - 0,4 п.л.
19. Матвеев Р.И. Стратегические взаимодействия компаний в модели асимметричной дуополии и национальное благосостояние // Современные научные исследования. - 2007, № 2. - 0,5 п.л.
20. Матвеев Р.И. Государственное регулирование интеллектуальной собственности и скорость инновационного процесса // Современные научные исследования. - 2007, № 4. - 0,5 п.л.
21. Матвеев Р.И., Чепиков Э.В. Оптимизация срока действия патента // Современные научные исследования. - 2007, № 3. - 0,5 п.л. (в т.ч. автора 0,25 п.л.).
22. Матвеев Р.И. Прогнозирование влияния скорости действия патента на скорость инновационного процесса и национальное благосостояние // Тенденции, проблемы и перспективы развития социально-экономических систем (межвузовский сборник научных трудов) - М.: МИСОН, 2008. - 0,5 п.л.
23. Матвеев Р.И. Моделирование и анализ олигополистической конкуренции в сфере научно-исследовательских разработок // Современные научные исследования. - 2008, № 1. - 0,5 п.л.
24. Матвеев Р.И. Модели оптимального инвестирования в условиях неопределенности // Тенденции, проблемы и перспективы развития социально-экономических систем (межвузовский сборник научных трудов) - М.: МИСОН, 2008. - 0,5 п.л.
25. Матвеев Р.И. Моделирование инвестирования в новые технологии в условиях неопределенности и конкуренции // Современные научные исследования. - 2009, № 4. - 0,8 п.л.
26. Матвеев Р.И. Экономико-математическая модель инвестирования в инновации в условиях монополистической конкуренции // Сборник научных трудов Всероссийской научной конференции Актуальные проблемы социально-экономического развития. - Кисловодск: Издат. Центр КИЭП, 2009. - 0,3 п.л.
27. Матвеев Р.И. Конкуренция в инновационной сфере и оптимальный срок действия патента // Современная экономика: проблемы и решения. Ц2010, № 3. Воронеж: Изд-во ВГУ.а - 0,5 п.л.
28. Дудов А.С., Матвеев Р.И. Прогнозирование рыночного лидерства в стохастических условиях // Международная научно-практическая конференция Экономическое прогнозирование: модели и методы. - Воронеж: ВГУ.а - Т. 1. - 2010. - 0,2 п.л. (в т.ч. автора 0,1 п.л.).
29. Дудов А.С., Матвеев Р.И. Анализ влияния срока действия патента на инвестиции в научно-исследовательский сектор // Сборник научных трудов Всероссийских научных чтений Математическая экономика и экономическая информатика. - Кисловодск: Изд-во РГЭУ (РИНХ), 2010. - 0,4 п.л. (в т.ч. автора 0,2 п.л.).
30. Матвеев Р.И. Равновесие Штакельберга в модели конкуренции за разработку инновации // Современные научные исследования. - 2010, № 2. - 0,7 п.л.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

     Авторефераты по всем темам  >>  Авторефераты по экономике