Все авторефераты докторских диссертаций
Все авторефераты докторских диссертаций
Теоретические основы экспериментальной реализации метода термомеханических аналогий для определения термонапряженного состояния в неоднородных элементах машиностроительных конструкций
Автореферат докторской диссертации
На правах рукописи
Иванов Андрей Сергеевич
Теоретические основы экспериментальной реализации метода термомеханических аналогий для определения термонапряженного состояния в неоднородных элементах машиностроительных конструкций
с объемным тепловыделением
Специальность 01.02.04 - Механика деформируемого твердого тела
Автореферат диссертации на соискание ученой степени
доктора технических наук
Москва 2012
а
Работа выполнена в Московском государственном открытом университете имени В.С. Черномырдина
Научный консультанта - доктор технических наук, профессор Федик И.И.
Официальные оппоненты:
- доктор технических наук, профессор Морозов Е.М.,
- доктор физико-математических наук, профессор Ивлев Д.Д.,
- доктор технических наук, профессор Гетман А.Ф.
а Ведущая организация - ОАО ОКБ ГИДРОПРЕСС, г. Подольск, Московская область, ул. Орджоникидзе, 21
а Защита состоитсяа л 29 аамаяаа 2012г. аав 15.00 часов на заседании
диссертационного совета Д 212.137.02 в Московском государственном открытом университете имени В.С. Черномырдина по адресу:
107996 Москва, ул. П. Корчагина, д.22;
Е-mail: msou@msou.ru.
С диссертацией можно ознакомиться в библиотеке МГОУ имени В.С. Черномырдина
Автореферат разослан л_____а апреляа 2012
Ученый секретарь
диссертационного совета Н.В. Лукашина
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
а Актуальность темы. Современный уровень развития промышленности и строительства характеризуется широким использованием технических конструкций, работающих в сложных условиях термического и силового нагружений. Прочностная надежность, безопасность эксплуатации и ресурс таких изделий определяется уровнем и характером распределения внутренних температурных напряжений, что требует анализа напряженно-деформированного состояния ответственных элементов конструкций. Также серьезной проблемой создания конкурентоспособной современной техники является обеспечение высокого качества и необходимой точности разрабатываемых конструкций. Для этого необходимо еще на стадии проектирования учитывать особенности комплексного цикла технология - конструкция - эксплуатация. Такой подход должен быть применим к изделиям, работающим в условиях высоких температур и давлений, к которым относятся машиностроительные конструкции с объемным тепловыделением.
Изделия атомной техники (например, тепловыделяющие элементы ядерных реакторов) работают в условиях температурных перепадов с высокими градиентами, облучения и химически активных сред. Жесткие условия эксплуатации сопровождаются необратимыми изменениями теплофизических, механических и прочностных характеристик используемых материалов.
В металлургическом производстве качество литейных изделий во многом зависит от выбора режимов теплообмена, который позволяет регулировать тепловыделение при формообразовании отливки, тем самым, обеспечивая направленную кристаллизацию жидкого расплава с последующим равномерным остыванием отливки. Распределение температурных напряжений в сформировавшейся твердой заготовке существенно влияет на качество литых изделий и вызывает немалый интерес у специалистов.
В связи с этим актуальным является разработка расчетно-экспериментального метода исследования и моделирования термонапряженного состояния элементов машиностроительных конструкций при объемном тепловыделении с учетом переменных свойств материала, особенностей геометрической формы и условий эксплуатации.
Проведение вышеуказанных исследований безусловно способствует повышению прочностной надежности, безопасности эксплуатации, увеличению эксплуатационного ресурса машиностроительных конструкций, работающих в условиях действия высоких температур и силовых факторов, созданию конкурентоспособной техники, что полностью соответствует Приоритетным направлениям развития науки, технологий и техники в Российской Федерации, и Перечню критических технологий Российской Федерации, утвержденным Президентом РФ от 7 июля 2011 года Пр-№ 899.
Одним из основных источников появления температурных напряжений в исследуемых конструкциях является неоднородная деформация, возникающая вследствие неоднородностей, к которым можно отнести физико-механические процессы (неоднородное тепловыделение, излучение и т.д.), геометрические неоднородности (форма конструкции, наличие различных отверстий, вырезов, перепады толщин, разностенность и пр.) и неоднородную структуру материала. Их определение в подобных системах встречает математические трудности. Существующие аналитические и численные методы не охватывают широкий спектр разнообразных причин появления неоднородной деформации материала и их характеристик, существенно влияющих на уровень температурных напряжений. Создание новых адекватных расчетных моделей исследуемых объектов позволяет применять аналоговые и экспериментальные методы исследования термонапряженного состояния. Дальнейшая разработка таких методов и их сочетание в исследованиях требуют строгого теоретического обоснования на основе единого математического аппарата. Такой подход при определении температурных напряжений основан на математических аналогиях в механике деформируемого твердого тела. Использование единого математического формализма при описании физических явлений и напряженно-деформированного состояния в различных конструктивных схемах позволяет использовать математические аналогии для решения конкретных задач. При этом определяющим направлением исследований является экспериментальная реализация термомеханических аналогий, которая позволяет моделировать термонапряженное состояние и проводить оценку предельных уровней температурных напряжений в машиностроительных конструкциях с объемным тепловыделением. Отсюда с очевидностью вытекает
Актуальность темы диссертационной работы.
а Целью работы является разработка, теоретическое обоснование и практическая реализация расчетно-экспериментального метода исследования температурных напряжений в машиностроительных конструкциях с объемным тепловыделением на основе математических аналогий в механике деформируемого твердого тела. Для достижения указанной цели поставлены и решены следующие основные задачи:
- дано математическое обоснование расчетно-экспериментального метода определения температурных напряжений в неоднородных элементах машиностроительных конструкциях с объемным тепловыделением на основе использования математических аналогий в механике деформируемого твердого тела;
- разработаны и практически апробированы тестовые системы при моделировании температурных напряжений в элементах конструкций с переменными характеристиками, такими как, свойства материала, параметры эксплуатации, геометрическая форма;
- разработаны оригинальные методики экспериментального моделирования температурных напряжений и средства технического оснащения для проведения модельных экспериментов;
- проведены экспериментальные исследования термонапряженного состояния машиностроительных конструкций с переменными характеристиками и неоднородной структурой материала с учетом условий объемного тепловыделения на основе метода термомеханических аналогий.
а Научная новизна результатов работы заключается в следующем:
- теоретически обоснован и экспериментально реализован метод определения температурных напряжений в неоднородных элементах машиностроительных конструкциях с объемным тепловыделением путем использования математических аналогий в механике деформируемого твердого тела;
- осуществлен единый подход к моделированию температурных напряжений в элементах конструкций с отверстиями и вырезами различной конфигурации путем изменения координатных осей внутреннего контура эллиптического профиля;
- разработан и математически обоснован аналоговый метод определения температурных напряжений в изделиях с переменными характеристиками и неоднородной структурой материала;
- впервые предложена и экспериментально обоснована методика определения термонапряженного состояния корпусных элементов энергоаппаратов с учетом реальной конструкции наиболее ответственных узлов моделируемой системы.
а Достоверность полученных результатов обеспечивается корректностью моделирования температурных напряжений в различных конструктивных схемах на основе использования математических аналогий в механике деформируемого твердого тела. Тестовые примеры, компьютерная проверка разработанных алгоритмов, а также хорошая корреляция теоретических и модельно экспериментальных исследований с максимальной погрешностью, не превышающей 10%, в достаточно полной мере гарантируют обоснованность и достоверность результатов диссертационной работы.
а Практическая значимость диссертационной работы заключается в разработке расчетно-экспериментального метода определения температурных напряжений в неоднородных элементах машиностроительных конструкциях с объемным тепловыделением с использованием математических аналогий в механике деформируемого твердого тела. Проведено строгое математическое обоснование корректности разработанной методики экспериментальной реализации математических аналогий при определении температурных напряжений в неоднородных конструкциях с объемным тепловыделением. На основе проведенных исследований выработаны практические рекомендации по снижению уровня термонапряжений в изделиях атомной техники.
а Результаты диссертационной работы внедрены в расчетную практику заинтересованных организаций и используются при проектировании изделий новой техники, что подтверждено актами и справками внедрения от предприятий: 1. ОАО НИКИЭТ, г. Москва, 2011 г. 2. ЗАО НТЦ Бакор, г. Щербинка Московской области, 2011 г. 3. Филиал ГУП КБП ЦКИБ СОО, г. Тула, 2011 г. 4. ЗАО Сибкабель г. Подольск Московской области, 2011 г. 5. Филиал ОАО Центротрансжелезобетон Силикатненский завод ЖБК г. Подольск Московской области, 2011 г. 6. ООО ЭКОТЕКА, г. Лыткарино Московской области, 2011 г.
На защиту выносятся:
- математическое обоснование расчетно-экспериментального метода определения температурных напряжений в неоднородных элементах машиностроительных конструкциях с объемным тепловыделением элементах конструкций на основе использования математических аналогий в механике деформируемого твердого тела;
- единый подход к анализу температурных напряжений в изделиях атомной техники с переменными характеристиками, включая свойства материала, параметры эксплуатации, геометрическую форму, а также неоднородность структуры материала;
- результаты экспериментальной реализации термомеханических аналогий в механике деформируемого твердого тела при моделировании напряженно-деформированного состояния элементов конструкции атомной техники, металлургического производства и крупногабаритных строительных конструкций;
- практические рекомендации по снижению уровня температурных напряжений в изделиях новой техники для обеспечения прочностной надежности и увеличения ресурса эксплуатации.
Апробация работы. Основные положения и результаты диссертационной работы докладывались и обсуждались на следующих конференциях и семинарах: 1. XII Международный семинар Технологические проблемы прочности, г. Подольск, 2005 г. 2. XIII Международный семинар Технологические проблемы прочности, г. Подольск, 2006 г. 3. XIV Международный семинар Технологические проблемы прочности, г. Подольск, 2007 г. 4. XV Международный семинар Технологические проблемы прочности, г. Подольск, 2008 г. 5. XVI Международный семинар Технологические проблемы прочности, г. Подольск, 2009 г. 6. XVII Международный семинар Технологические проблемы прочности, г. Подольск, 2010 г. 7.V Международная научная конференция Прочность и разрушение материалов и конструкций, г. Оренбург, 2008 г. 8. II Международная научная конференция Современные проблемы математики и механики, г.Львов, 2008 г. 9. ХVIII Петербургские чтения по проблемам прочности и роста кристаллов г. Санкт-Петербург, 2008 г. 10. V Международная конференция Фазовые превращения и прочность кристаллов, г. Черноголовка, 2008 г. 11. Международная научно-техническая конференция Нанотехнологии и наноматериалы, г. Москва, 2009 г. 12. Первые Московские чтения по проблемам прочности, г. Москва, 2009 г. 13. Х Всероссийский Симпозиум по прикладной математике, г. Санкт-Петербург, 2009 г. 14. Х Всероссийский Симпозиум по прикладной математике, г. Дагомыс, 2009 г. 15 ХХ Петербургские чтения по проблемам прочности, г. Санкт-Петербург, 2010 г. 16. V-я Евразийская научно-практическая конференция Прочность неоднородных структур, г. Москва, 2010 г. 17. ХI Всероссийский Симпозиум по прикладной математике, г. Кисловодск, 2010 г. 18. VI Всероссийская научно-практическая конференция Актуальные задачи математического моделирования и информационных технологий, г. Сочи, 2010 г. 19. ХI Всероссийский Симпозиум по прикладной математике, г. Дагомыс, 2010 г. 20. 3-й Международный форум по интеллектуальной собственности EXPOPRIORITY-2011, г. Москва. 21. Общеуниверситетский научный семинар Механика неоднородных структур и систем при МГОУ, 2011 г.
Публикации. По теме диссертации опубликовано 43 работы, включая 23 статьи, входящих в перечень ведущих рецензируемых научных журналов и изданий, рекомендованных ВАК РФ, а также 2 монографии.
Структура и объем работы. Диссертация изложена на 264 листах машинописного текста, состоит из введения, шести глав и списка литературы из 149 наименований и приложения, в котором представлены акты и справки внедрения результатов проведенных исследований, включая 22 таблицы и 76 рисунка.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
а Во введении обосновывается важность актуальной темы диссертационной работы, сформулирована цель диссертации и новизна проведенных исследований. Приведено краткое изложение содержания диссертации по главам.
а В первой главе диссертации приведен исторический обзор и анализ работ, посвященных исследованию термонапряженного состояния в данной тематике, рассмотрены основные конструктивные схемы, используемые материалы и условия эксплуатации неоднородных элементов машиностроительных конструкций с объемным тепловыделением. Основное внимание уделяется элементам конструкций атомной техники, изделиям металлургического производства. Необходимость такого выбора обусловлена следующими соображениями. Во-первых, перечисленные элементы конструкций работают в условиях температурных и силовых нагрузок. Поэтому прочностная надежность и их ресурс эксплуатации определяется уровнем и характером внутренних температурных напряжений. Во-вторых, упомянутые элементы конструкций в подавляющем большинстве допускают моделирование напряженно-деформированного состояния (НДС) в рамках механики деформируемого твердого тела (состояние плоской деформации или плоское напряженное состояние). И, наконец, последняя особенность таких конструктивных схем позволяет использовать математические аналогии в механике деформируемого твердого тела для определения соответствующих внутренних температурных напряжений.
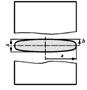
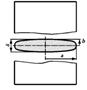
Основным конструктивным элементом ядерного реактора является активная зона, где размещены каналы с тепловыделяющими элементами. Форма и геометрические размеры последних зависят от назначения ядерного реактора. Наиболее распространенной формой является длинный цилиндрический стержень, заключенный в металлическую оболочку. Отдельные варианты сечений тепловыделяющих элементов приведены на рис.1.

Рис.1. Типовые конструкции тепловыделяющих элементов
а Для определения внутренних температурных напряжений в подобных конструктивных схемах вполне приемлемы соотношения плоской деформации теории упругости и термоупругости. Отдельные элементы конструкций атомной техники представляют собой перфорированные пластины (рис. 2). При этом характерный размер отверстий превышает толщину пластины. НДС таких систем определяют на основе использования соотношений для плоского напряженного состояния.
Для снижения уровня внутренних температурных напряжений предполагается использовать переменные характеристики изделия: свойства материала, параметры эксплуатации, геометрическую форму. Решение задач термоупругости для произвольно изменяющихся характеристик изделия представляет значительные математические трудности. Поэтому предполагается использовать математические аналогии в механике деформируемого твердого тела. Подробнее этот вопрос рассматривается в оригинальной части диссертационной работы.

Рис. 2. Пластины, перфорированные отверстиями; h<d; h<a<b
а Математические аналогии в механике деформируемого твердого тела дают возможность применять подобные системы при моделировании длинных стержней с внутренними цилиндрическими отверстиями. Если отверстия перфорированной пластины изменяют свою форму, то ее можно аппроксимировать эллиптическим сечением, которое моделирует достаточно широкий спектр сечений от круга до эллиптической трещины.
Изделия литейного производства широко применяются в современном машиностроении. Качество последних существенно зависит от тепловыделения в процессе формообразования литой заготовки, обеспечения направленной кристаллизации жидкого расплава посредством выбора оптимальных режимов теплообмена. Образование структурных дефектов приповерхностного слоя материала во многом зависит от возникающих температурных напряжений и приводит к снижению прочностных характеристик. Исследование термонапряженного состояния литых заготовок является сложной многофункциональной задачей. Поэтому возникает необходимость в разработке расчетно-экспериментального метода анализа температурных напряжений на основе математических аналогий в механике деформируемого твердого тела. Такой метод позволит определять с приемлемой для практических целей точностью напряженно-деформированное состояние изделий литейного производства.
Анализ конструктивных схем рассматриваемых изделий и условий их эксплуатации позволяет выделить некоторые особенности, которые являются для них общими. Это возникновение температурных напряжений при объемном тепловыделении. Данный процесс существенно влияет на прочностную надежность и ресурс эксплуатации рассматриваемых конструкций. Неоднородная структура материала также является источником внутренних напряжений при силовом и температурном нагружениях. Показана принципиальная возможность использования математических аналогий механики деформируемого твердого тела для определения внутренних температурных напряжений различной физической природы. Дается постановка задачи проведения исследований термонапряженного состояния выбранных элементов конструкций на основе экспериментальной реализации метода термомеханических аналогий.
Некоторые обобщенные конструктивные схемы для исследования НДС элементов рассматриваемых изделий приведены в итоговой таблице 1.
Таблица 1. Обобщенные конструктивные схемы для исследования напряженно-деформированного состояния элементов конструкций с учетом эксплуатационных, теплофизических и геометрических свойств
№ пп |
Конструктивная схема |
Область применения |
||
1. |
Поверхности второго порядка
|
Изделия атомной техники, материалы с переменными свойствами |
Продолжение таблицы 1
№ пп |
Конструктивная схема |
Область применения |
||||||
2. |
Цилиндрические поверхности
|
Изделия атомной техники с переменными характеристиками: -эксплуатационные, -теплофизические, -геометрические. Крупногабаритные строительные конструкции. Новые материалы
|
||||||
3 |
Оболочечные конструкции
|
Изделия атомной техники, элементы конструкций литейных изделий |
||||||
4. |
|
Изделия атомной техники, элементы конструкций литейного производства, элементы крупногабаритных строительных конструкций, композитные материалы |
||||||
а Вторая глава диссертационной работы посвящена описанию различных методов определения температурных напряжений в механике деформируемого твердого тела. Рассмотрены физические механизмы образования внутренних напряжений при изготовлении и эксплуатации элементов машиностроительных конструкций. Основными типами внутренних напряжений в условиях объемного тепловыделения являются температурные, поскольку рассматриваемые изделия подвергаются значительному тепловому воздействию. Источником внутренних напряжений являются также структурные неоднородности материала, которые наиболее отчетливо проявляются в наноматериалах.
Для теоретического обоснования разрабатываемого метода рассмотрены общие уравнения термоупругости. Получены условия, при выполнении которых, имеет место аналогия квазистатической задачи термоупругости изотермическим задачам теории упругости.
Рассмотрены преимущества и недостатки основных методов определения температурных напряжений (аналитических, численных, экспериментальных) с позиции математических аналогий механики деформируемого твердого тела.
Под внутренними температурными напряжениями в механике деформируемого твердого тела понимают разновидность напряжений, появление которых обусловлено взаимодействием системы с различными физическими полями. Такие напряженияа рассматривают в качестве дополнительных к основному напряженному состоянию. Соответствующие уравнения теории упругости для изотропного случая записываются в виде
![]() ;
; ![]()
![]() ;
; ![]() аа(1)
аа(1)
![]() ;
; ![]() ,
,
где eхх , eуу , ezz , gху , gуz , gzx - компоненты тензора деформаций; sхх , sуу , szz , tхy, tуz , tzx - компоненты тензора напряжений; Е - модуль Юнга, m - модуль сдвига; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() а- дополнительные деформации, обусловленные структурными, фазовыми и другими превращениями, a - коэффициент температуропроводности,
а- дополнительные деформации, обусловленные структурными, фазовыми и другими превращениями, a - коэффициент температуропроводности, ![]() - коэффициент Пуассона, Т - температура.
- коэффициент Пуассона, Т - температура.
Численный анализ внутренних температурных напряжений в неоднородных элементах конструкций на основе соотношения (1) встречает существенные математические трудности. Аналитические методы определения внутренних температурных напряжений наиболее эффективны при анализе элементов конструкций простой геометрической формы: сферической, цилиндрической, эллиптической. Координатные и временные зависимости неоднородной деформации могут быть получены из решения уравнений теплопроводности и диффузии. Начальные и граничные условия соответствующих уравнений гарантируют однозначность полученных решений и достоверность определения внутренних температурных напряжений в рамках механики деформируемого твердого тела. Полученные решения могут использоваться в качестве тестовых примеров при реализации численных или экспериментальных методов определения внутренних напряжений.
Для иллюстрации рассмотрена задача определения температурных напряжений в тепловыделяющем элементе эллиптического поперечного сечения (состояние плоской деформации). Выбор такой модельной системы обусловлен тем, что за счет изменения полуосей эллипса удается получить весьма широкий спектр сечений: от округлости до тонкой пластины. Соответствующая задача определения термонапряженного состояния математически формулируется следующим образом
![]() ,
, ![]() апри
апри ![]() ,
,
![]() ,аа (2)
,аа (2)
где F - функция напряжений; ![]() а- коэффициент температуропроводности; Е - модуль Юнга;
а- коэффициент температуропроводности; Е - модуль Юнга; ![]() а- мощность объемного тепловыделения, a иb - полуоси эллипса;sхх , sуу , szz - компоненты тензора напряжений;
а- мощность объемного тепловыделения, a иb - полуоси эллипса;sхх , sуу , szz - компоненты тензора напряжений; ![]() а- коэффициент теплопроводности. Величина szz справедлива для свободных торцевых поверхностей. Граничные условия на границе эллиптического сечения записаны для свободных от нагрузок боковых поверхностей.
а- коэффициент теплопроводности. Величина szz справедлива для свободных торцевых поверхностей. Граничные условия на границе эллиптического сечения записаны для свободных от нагрузок боковых поверхностей.
Задача (2) имеет точное аналитическое решение (табл. 2) и поэтому может служить тестовым примером при использовании математических аналогий механики деформируемого твердого тела.
Таблица 2. Аналитический метод определения внутренних напряжений в тепловыделяющих элементах атомной техники
№ п.п. |
Конструктивная схема |
Уравнения к решению поставленной задачи |
Точные аналитические решения |
1 |
2 |
3 |
4 |
1 |
ТВЭЛ шаровидной формы
|
|
|
2 |
ТВЭЛ с поперечным сечением круговой формы
|
при
|
|
3 |
ТВЭЛ с поперечным сечением эллиптической формы
|
при
|
|
4 |
ТВЭЛ с попе-речным сечением эллиптической формы, переходящий в пластину
|
а >> b |
|
а Для многосвязной области (длинные каналы произвольного сечения) функция напряжений должна удовлетворять условиям Митчелла термоупругой задачи: однозначность перемещений и угла поворота на границе внутренних контуров. Если постоянные правой части бигармонического уравнения зависят от координат, то получение аналитического решения уравнения (2) не представляется возможным. В этом случае применяются численные методы или используют математические аналогии.
Среди перспективных методов определения внутренних температурных напряжений заслуживает внимания математические аналогии механики деформируемого твердого тела. Математическая формулировка задачи (2) с точностью до обозначений совпадает с задачей изгиба жестко защемленной по внешнему контуру пластины идентичной конфигурации.
![]() ,
, ![]() апри
апри ![]() ,а (3)
,а (3)
где w - функция прогиба пластины, P(x,y) - распределенная нагрузка. D - жесткость пластины. Задачи (2) и (3) математически идентичны. Поэтому из решения задачи (3) можно получить компоненты тензора напряжений.
![]() ,
, ![]() ,а (4)
,а (4)
где ![]() а- коэффициент для сохранения размерности
а- коэффициент для сохранения размерности ![]() . При этом закон нагружения модельной пластины определяется соотношением
. При этом закон нагружения модельной пластины определяется соотношением
![]() (5)
(5)
Точные решения аналитического метода определения внутренних напряжений в выбранных конструктивных схемах представлены в таблице 2. Если осуществляют моделирование многосвязной области, то к внутренним контурам прикладывают сосредоточенные силы и моменты (по аналогии с условиями Митчелла термоупругой задачи).
Для экспериментальной реализации термомеханических аналогий предложено модельную пластину нагрузить по закону (5) и далее измерить прогиб пластины w. Функцию прогиба аппроксимируют наиболее приемлемым выражением и для определения компонент тензора термонапряжений применяют соотношения (4). Построение искомой функции прогиба по экспериментальным точкам осуществляется в том случае, когда неизвестно аналитическое решение задачи.
Рассмотрены математические аналогии в решении задач термоупрости для оболочечных конструкций. Показано, что наиболее эффективным методом определения температурных напряжений в них является метод термомеханических аналогий, основанный на решении несвязанной задачи термоупругости в квазистатической постановке, когда известное распределение температур в исследуемых объектах при соблюдении соответствующих граничных условиях позволяет определить компоненты вектора смещения.
Третья глава диссертационной работы посвящена теоретическому обоснованию метода термомеханических аналогий при определении внутренних температурных напряжений в элементах конструкций с переменными характеристиками. Многие реальные конструкции выполнены из материалов, обладающих анизотропными свойствами. К последним относятся конструкционные материалы ядерной техники. Анизотропия присуща теплофизическим и механическим характеристикам материала. Определение температурных напряжений в исследовании таких материалов позволяет математическая аналогия, когда с точностью до обозначений задача термоупругости совпадет с задачей изгиба пластины. Появляются возможности на основе метода термомеханической аналогии моделировать термонапряженное состояние в ортотропном длинном цилиндре, В табл.3. приведено решение задачи прямоугольной анизотропии.
Среди теплофизических свойств материала определяющая роль принадлежит коэффициенту линейного расширения. Эта характеристика материала определяет уровень температурных напряжений при тепловом нагружении элементов конструкций. Объемное тепловыделение в изделиях атомной техники, строительных конструкций, изготовленных в полевых условиях, также приводит к появлению термонапряжений, величина которых зависит от коэффициента линейного расширения. Его величина изменяется в достаточно широком диапазоне по сравнению с упругими свойствами, которые также характеризуют термонапряженное состояние изделий различных изделий.
Таблица 3. Экспериментальная реализация термомеханических аналогий для анизотропных материалов
№ п.п. |
Переменный параметр |
Экспериментальная реализация термомеханических аналогий при [F]=[?w] |
||
Математическая аналогия |
Модельные нагрузки |
|||
1 |
Прямоугольная анизотропия |
Пластина Односвязная область
|
Функция напряжений
Функция прогиба
|
|
Пластина Многосвязная область
|
Функция напряжений
Функция прогиба
|
|
||
Неоднородность рассматриваемой теплофизической характеристики изменяет характер распределения термонапряжений. Показана принципиальная возможность снижения уровня термонапряжений в тепловыделяющем цилиндре с переменным коэффициентом линейного расширения, изменяющимся по закону
![]() , (6)
, (6)
где R - радиус цилиндра.
В соотношении (6) бигармоническое уравнение для функции напряжений имеет точное аналитическое решение в виде
![]() .аа (7)
.аа (7)
Соответствующие компоненты тензора термонапряжений определяются из соотношений (цилиндрическая система координат)
![]() ;аа
;аа ![]() ;
;
![]() ;
; ![]() .а (8)
.а (8)
Выражение для ![]() справедливо для свободных от нагрузок торцевых поверхностей цилиндра. Используя соотношение
справедливо для свободных от нагрузок торцевых поверхностей цилиндра. Используя соотношение ![]() , приведено сравнение термонапряжений
, приведено сравнение термонапряжений ![]() адля постоянного и переменного значения
адля постоянного и переменного значения ![]() . Графические зависимости
. Графические зависимости ![]() (постоянное значение
(постоянное значение ![]() ) и
) и ![]()
![]() а(переменное значение
а(переменное значение ![]() ) приведены на рисунках 3 и 4.
) приведены на рисунках 3 и 4.
Рис. 3.Температурные напряжения: |
|
Рис.4. Приведенные термонапряжения для цилиндрического твэла с учетом изменения коэффициента линейного расширения.
а При прочих равных условиях переменные значения ![]() аснижают уровень температурных напряжений. Согласно математической аналогии в механике деформируемого твёрдого тела, функция напряжений F соответствует функции прогиба w жёстко защемленной по внешнему контуру пластины идентичной конфигурации. Координатная зависимость функции прогиба соответствует выражению (7) с учётом коэффициента размерности c соотношения
аснижают уровень температурных напряжений. Согласно математической аналогии в механике деформируемого твёрдого тела, функция напряжений F соответствует функции прогиба w жёстко защемленной по внешнему контуру пластины идентичной конфигурации. Координатная зависимость функции прогиба соответствует выражению (7) с учётом коэффициента размерности c соотношения ![]() . Закон нагружения модельной пластины подчиняется параболической зависимости и возрастает по мере продвижения к границе области. Такая зависимость имеет вид
. Закон нагружения модельной пластины подчиняется параболической зависимости и возрастает по мере продвижения к границе области. Такая зависимость имеет вид
![]() ,а (9)
,а (9)
Точное аналитическое решение задач термоупругости и изгиба пластины может служить тестовым примером при моделировании внутренних напряжений при произвольном изменении коэффициента линейного расширения.
Мощность объёмного тепловыделения в изделиях атомной техники является параметром эксплуатации. Этот параметр также определяет уровень и характер распределения температурных напряжений. При изменении координатной зависимости объёмного тепловыделения происходит изменение соответствующих термонапряжений.
Принципиальная возможность снижения уровня температурных напряжений при использовании эксплуатационной характеристики иллюстрируется на примере тепловыделяющего цилиндра с постоянным коэффициентом линейного расширения. Если мощность объёмного тепловыделения описывается параболической зависимостью от радиальной координаты
![]() а(10)
а(10)
то соответствующая функция напряжений для состояния плоской деформации принимает вид
![]() а(11)
а(11)
где ![]() а- постоянный коэффициент линейного расширения. Остальные обозначения остаются неизменными. Отличие соотношений (11) и (7) обусловлено разными значениями правых частей бигармонических уравнений для соотношений (6) и (10), которые получают из решения уравнений теплопроводности. Для выражений (6) и (11) правые части бигармонических уравнений записываются соответственно
а- постоянный коэффициент линейного расширения. Остальные обозначения остаются неизменными. Отличие соотношений (11) и (7) обусловлено разными значениями правых частей бигармонических уравнений для соотношений (6) и (10), которые получают из решения уравнений теплопроводности. Для выражений (6) и (11) правые части бигармонических уравнений записываются соответственно
![]() аиа
аиа ![]() .а а(12)
.а а(12)
Компоненты тензора термонапряжений для переменной мощности объемного тепловыделения в цилиндре определяется соотношениями по аналогии с (8)
![]() ;
; ![]() ;
;
![]() ;
; ![]() .аа а(13)
.аа а(13)
Точное аналитическое решение задачи термоупругости для принятого закона объёмного тепловыделения может служить тестовым примером при моделировании внутренних температурных напряжений на основе математических аналогий в механике деформируемого твердого тела. Функцияа напряжений F соотношения (11) соответствует функции прогиба жёстко защемленной пластины w идентичной формы.
Экспериментальная реализация термомеханических аналогий для исследования изделий с переменными характеристиками приведены в табл. 4.
Среди переменных характеристик элементов конструкций заслуживают внимания геометрическая форма соответствующих систем. При изменении геометрии изделия меняется и характер распределения температурных напряжений. Математические аналогии наиболее приемлемы при моделировании термонапряжений в элементах конструкций эллиптического поперечного сечения (состояние плоской деформации).
В качестве иллюстрации рассмотрено термонапряженное состояние тепловыделяющего цилиндра эллиптического поперечного сечения. Такую геометрию можно рассматривать как изменение формы цилиндрического сечения при сохранении площади поперечного сечения и мощности объемного тепловыделения. Эллиптическая форма поперечного сечения дает возможность рассматривать достаточно широкий диапазон изменения геометрии элементов конструкции (от круга до протяженной эллиптической трещины).
Приведены аналитические зависимости для компонент тензора термонапряжений в тепловыделяющих цилиндрах кругового и эллиптического поперечных сечений. Показано, что при сохранении площади поперечного сечения и мощности объемного тепловыделения максимальные термонапряжения возникают в тепловыделяющих элементах кругового поперечного сечения.
Таблица 4. Экспериментальная реализация термомеханических аналогий для переменных параметров коэффициента линейного расширения и объемного тепловыделения
№ п.п. |
Переменный параметр |
Экспериментальная реализация термомеханических аналогий при [F]=[?w] |
||
Математическая аналогия |
Модельные нагрузки |
|||
1 |
Коэффициент линейного расширения a |
Круглая пластина Односвязная область
|
Функция напряжений
Функция прогиба
|
При ?=?0
При ???0
|
2 |
Объемное тепловыделение q |
Круглая пластина Односвязная область
|
Функция напряжений
Функция прогиба
|
При q=q0
При q?q0
|
а Компоненты тензора термонапряжений для кругового и эллиптического сечений получают из решения задач термоупругости для упомянутых областей. Если границы области описываются кривыми второго порядка (окружность, эллипс), то бигармоническое уравнение для функции напряжений имеет точное аналитическое решение. Сравнительный анализ соответствующих компонентов тензора напряжений приведен для sхх. Отношение двух значений термонапряжений описывается выражением
 ,аа (14)
,аа (14)
где ![]() аЦтермонапряжение для эллиптического сечения,
аЦтермонапряжение для эллиптического сечения, ![]() - соответствующее термонапряжение для кругового сечения; а и b - полуоси эллипса. Анализ соотношения (14) показывает, что при одинаковых свойствах материала и параметров эксплуатации уровень термонапряжений при изменении формы из круга в эллипс уменьшается. Указанная особенность распределения термонапряжений позволяет управлять термонапряженным состоянием изделий путем изменения их геометрической формы
- соответствующее термонапряжение для кругового сечения; а и b - полуоси эллипса. Анализ соотношения (14) показывает, что при одинаковых свойствах материала и параметров эксплуатации уровень термонапряжений при изменении формы из круга в эллипс уменьшается. Указанная особенность распределения термонапряжений позволяет управлять термонапряженным состоянием изделий путем изменения их геометрической формы
а В четвертой главе диссертационной работы рассмотрено применение математических аналогий в механике деформируемого твердого тела для определения внутренних напряжений в элементах конструкций с неоднородной структурой материала. Среди неоднородностей структуры ведущее место занимают выделения новой фазы произвольной конфигурации и широкого диапазона характерных размеров. В окрестности подобных структурных неоднородностей возникают поля внутренних напряжений. Для улучшения прочностных характеристик изделий применяют покрытия. Материал покрытия характеризуетсяа свойствами, которые отличаются от свойств материала изделий. При термосиловом нагружении возникают внутренние напряжения, которые могут снижать преимущества покрытий.
Во многих случаях рассматривают структуры, состоящие из мелких зерен (наноразмерного диапазона) и крупных зерен (микронного характерного размера). Такое сочетание характерных размеров рассматривается как неоднородная структура материала. При этом крупные зерна находятся в окружении наноразмерных зерен с иным набором теплофизических, упругих и прочностных характеристик. Несогласованность свойств сопровождается появлением внутренних напряжений. Для определения внутренних напряжений в материалах с неоднородной структурой вполне применимы математические аналогии в механике деформируемого твердого тела.
Рассмотрено выделение новой фазы произвольного поперечного сечения (состояние плоской деформации) с другим параметром кристаллической решетки. Несогласованность последних сопровождается появлением внутренних напряжений в окружающей матрице и в самой новой фазе. Параметр кристаллической решетки является непрерывной функцией радиальной координаты (рис.5-а) и описывается соотношением
![]() ,а аа(15)
,а аа(15)
где ![]() а- параметр кристаллической решетки в центре структурной неоднородности,
а- параметр кристаллической решетки в центре структурной неоднородности, ![]()
![]() а- угловая зависимость радиуса неоднородности, r
а- угловая зависимость радиуса неоднородности, r![]() аугловая зависимость текущего размера рассматриваемой области. Отклонение
аугловая зависимость текущего размера рассматриваемой области. Отклонение ![]() аменяется непрерывно при переходе через межфазную границу.
аменяется непрерывно при переходе через межфазную границу.
Функция напряжения для непрерывного изменения параметра кристаллической решетки находится из решения бигармонического уравнения в односвязной области
 , аа
, аа![]() апри аr = R,а (16)
апри аr = R,а (16)
где R - внешняя граница рассматриваемой области.
Предполагается, что эти характеристики материала одинаковы для выделения и окружающий матрицы. Математические аналогии в механике деформируемого твердого тела позволяют сформулировать соответствующую задачу для функций прогиба жестко защемленной пластины такой же конфигурации
![]() ,
, ![]() при r=R,аа (17)
при r=R,аа (17)
где - w функция прогиба пластины, D - жесткость пластины, P(r,j) - закон изменения распределенной нагрузки. С точностью до размерного множителя соотношения ![]() азадачи (16) и (17) математически эквиваленты. Это позволяет экспериментально определить функцию прогиба модельной пластины и приближенно описать ее приемлемой аналитической зависимостью.
азадачи (16) и (17) математически эквиваленты. Это позволяет экспериментально определить функцию прогиба модельной пластины и приближенно описать ее приемлемой аналитической зависимостью.
Для определения компонентов тензора внутренних напряжений применяют известные соотношения. Закон нагружения модельной пластины находится из равенства правых частей бигармонических уравнений
 .а (18)
.а (18)
Графическая зависимость соотношений (18) для конкретного угла ? приведена на рис 5-б. Геометрическая форма новой фазы зависит от несоответствия параметров кристаллической решетки при переходе через многофазную границу. При малом отклонении в параметрах решетки образуются, как правило, выделения сферической формы. По мере увеличения рассогласованности параметров решетки форма выделения становится эллипсоидальной. Именно в этом случае возникает высокий уровень внутренних напряжений.
Аналитическое решение
а |
Закон нагружения модельной пластины
б |
Рис. 5. Математические аналогии в исследовании структурной стабильности наноматериалов
а Для увеличения ресурса эксплуатации изделий применяют покрытия. Изделия при их наличии принадлежат к неоднородным структурам. Определение внутренних напряжений в подобных системах осуществляется на основе математических аналогий в механике деформируемого твердого тела. Такое моделирование внутренних напряжений наиболее приемлемо для состояния плоской деформации, когда характерный размер элемента конструкции в одном направлении существенно превышает таковой в других направлениях.
В качестве иллюстрации выбраны оболочки тепловыделяющих элементов цилиндрической формы. При изменении геометрии (цилиндр > эллипс) в материале оболочек возникают внутренние напряжения. Для их определения также используют математические аналогии в механике деформируемого твердого тела. Приведены соответствующие зависимости и тестовые примеры моделирования внутренних напряжений в элементах конструкций с покрытиями произвольной формы.
Наноструктурные материалы занимают принадлежащее им место в различных технических системах. Среди многообразия последних следует отметить использование наностуктур в сочетании с макроскопическими параметрами. Так, например, наноструктурная прослойка материала может окружать обычный поликристаллический материал. Такая неоднородная структура характеризуется различными значениями теплофизических, упругих и прочностных свойств поликристалла и его окружения в виде наноструктурной оболочки. При силовом или температурном нагружениях в элементах конструкций с упомянутой неоднородной структурой возникают внутренние напряжения. Рассмотрены вопросы в моделировании последних на основе математических аналогий в механике деформируемого твердого тела. При этом предполагается, что все перечисленные свойства неоднородного материала плавно меняются при переходе через разделяющую границу. В этом случае при моделировании внутренних напряжений можно рассматривать односвязную область. При таком подходе существенно упрощается практическая реализация модельного эксперимента, так как в качестве модельных нагрузок не используются сосредоточенные силы и моменты. Распределенная нагрузка является непрерывной функцией координат.
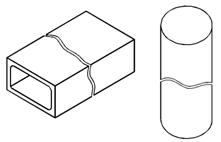
В пятой главе диссертационной работы теоретически обоснована адаптация метода термомеханических аналогий к расчетам элементов строительных конструкций. Ресурс эксплуатации крупногабаритных строительных конструкций зависит от распределения полей термонапряжений, которые возникают вследствие тепловыделения при затвердевании бетонной массы в полевых условиях, когда отсутствуют возможности проводить специальные технологии по снижению термонапряженного состояния изделия в заводских условиях. Крупногабаритные сооружения выполняют из бетона, железобетона и уникальных стальных металлоконструкций. Процессы раннего созревания бетона и неоднородности структуры являются источником внутренних температурных напряжений. Исследование термонапряженного состояния таких конструкций позволяет прогнозировать появление максимальных уровней термонапряжений и своевременно выявлять опасные сечения. Некоторые отдельные конструкции подобных сооружений приведены на рис. 6, 7.
Рис. 6. Некоторые конструкции плитного ростверка |
Рис. 7. Коробчатые и круглые аж/б элементы тоннелей |
а Приведены основы математической аналогии в исследованиях процессов объемного тепловыделения и термонапряженного состояния элементов строительных конструкций большой протяженности. Они заключаются в полном совпадении дифференциальных уравнений плоской теории термоупругости для функции напряжения F в брусе и функция прогиба пластины w. Показано, что метод термомеханических аналогий может быть успешно применен в определении полей термонапряжений и деформаций железобетонных конструкций при их изготовлении в полевых условиях с учетом особенностей неоднородностей геометрической формы.
Шестая глава диссертационной работы посвящается практической реализации термомеханических аналогий в механике деформируемого твёрдого тела при моделировании температурных напряжений в неоднородных элементах машиностроительных конструкций с объемным тепловыделением. Основное внимание уделяется анализу термонапряженного состояния тепловыделяющих элементов с переменными характеристиками. Рассматривается возможность регулирования термонапряжений путем использования переменных характеристик строительных конструкций.
Корректность проведения эксперимента при анализе термонапряженного состояния изделий обеспечивается тестовыми примерами, которые имеют аналитическое решение. Приведены соответствующие аналитические и графические зависимости для функции прогиба модельной пластины. Координатная зависимость функции прогиба при моделировании термонапряжений с переменной мощностью объемного тепловыделения представлена на рис. 8.

Рис.8. Координатная зависимость прогиба пластины
а Рассмотрена практическая реализация термомеханических аналогий на конкретных примерах. Это позволяет осуществлять определение термонапряжений на модельных пластинах при комнатной температуре, а тепловые нагружения исследуемой конструкции заменять силовыми нагрузками (распределенное давление, сосредоточенные силы и моменты).
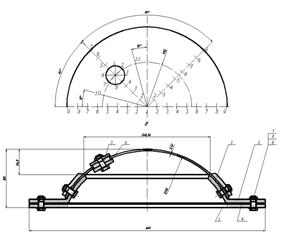
Приведена разработанная методика моделирования термонапряженного состояния панели корпуса энергоаппарата. Чертеж модели и монтажная схема измерительных датчиков представлены на рис. 9. Эпюры температурных напряжений в сечениях приведены на рис. 10. После нагружения модели системой нагрузок РК, ![]() , Му= 0 с помощью тензометрической аппаратуры замерялись главные деформации ех, еу. Температурные напряжения с учетом поправочного коэффициента к=РК/РМ определялись по формуле
, Му= 0 с помощью тензометрической аппаратуры замерялись главные деформации ех, еу. Температурные напряжения с учетом поправочного коэффициента к=РК/РМ определялись по формуле
 а, (19)
а, (19)
где y - тарировочный коэффициент, y = 0,0198 МПа/дел. прибора
панель корпуса
|
|
Аналоговая модель
|
Монтажная схема измерительных датчиков
|
Рис. 9. Панель корпуса энергоаппарата. Реальная конструкция, аналоговая модель и монтажная схема измерительных датчиков
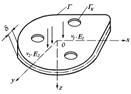
По результатам анализа выявлено, что внешний контур панели испытывает растягивающие напряжения, которые превалируют и в окрестностях контуров отверстий. В центральной части исследуемого объекта имеются сжимающие напряжения. Самым опасным сечением с точки зрения эксплуатационной характеристики является сечение Е-Е. Даются рекомендации по снижению уровня термонапряжений в этом сечении.

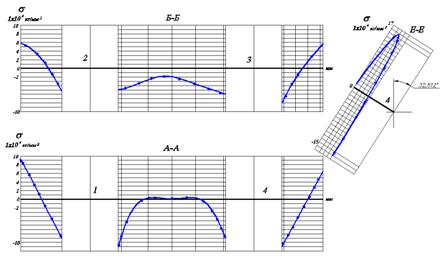

Рис. 10. Температурные напряжения в панели корпуса
а Осуществлено моделирование термонапряженного состояния литой заготовки оболочечной конструкции на примере отливки рефлектор (рис.11). Натурная конструкция имеет форму пологой оболочки с отверстиями на внешней поверхности. Модель выполнена из оргстекла, жестко защемлена по внешнему контуру, имеет абсолютно жесткие невесомые включения, моделирующие свободные от нагрузок отверстия, что позволяет обеспечивать строгое геометрическое подобие.
Производен выбор рабочих формул для нагружения модели механическими нагрузками, эквивалентными действию температурного поля.
Распределенные нагрузки |
Сосредоточенные нагрузки |
|
|
Отливка рефлектор
а |
Изотермическая модель
б |
Рис. 11. Натурная конструкция и изотермическая модель отливки рефлектор: а - аналоговая модель, б - монтажная схема установки тензодатчиков
Температурные напряжения для исследуемой оболочки определялись по формулам
 аа (20)
аа (20)
где ![]() а;
а; ![]() ,
, ![]() а- характерный размер и толщина модельной оболочки;
а- характерный размер и толщина модельной оболочки; ![]() аи
аи ![]() а- исследуемой оболочки.
а- исследуемой оболочки.
В ходе модельного эксперимента модель-оболочка была нагружена равномерным давлением р=0,04МПа, сосредоточенными силой Рмод = 2кГс, и моментом Ммод = 3кГс?см, приложенных к жестким включениям. Осуществлялись измерение деформаций ![]() аи
аи ![]() ана внутренней и внешней поверхности модели соответственно и пересчет их в температурные напряжения. Подсчитанные по формулам (20) температурные напряжения при
ана внутренней и внешней поверхности модели соответственно и пересчет их в температурные напряжения. Подсчитанные по формулам (20) температурные напряжения при
k =1 представлены на рис. 12.

Рис. 12. Распределение температурных напряжений свободного по контуру сферического сегмента от перепада температур по толщине оболочки с двумя отверстиями.
а Из графиков видно, что внешняя поверхность оболочки испытывает растягивающие температурные напряжения (кольцевые и радиальные), внутренняя поверхность наоборот - сжимающие. Наиболее опасным сечением в исследуемой конструкции будут сечения, проходящие от центра отверстий к внешнему контуру оболочки.
Универсальность разработанной методики позволяет моделировать температурные напряжения в сложных элементах конструкций с объемным тепловыделением. Приведены результаты моделирования напряженно-деформированного состояния крупногабаритных строительных конструкций при их сооружении в полевых условиях. Техника проведения эксперимента при моделировании температурных напряжений в бетонных сооружениях не отличается от рассмотренных ранее изделий атомной техники. Распределение температурных напряжений в сечениях ригеля приведены на рис.13.


Рис. 13. Температурные напряжения в сечениях ригеля
а Разработана методика экспериментального моделирования термонапряженного состояния исследуемого объекта, имеющего на внешней поверхности тонкие тоннельные вырезы, имитирующие теоретическую трещину. Исследования проводились на модели-аналоге рис.14, где контуры выреза имитировались невесомыми жесткими включениями. Рассматривалось два случая: 1случай - расположение выреза по радиусу пластины; 2 случай - по кольцу. Модель и монтажная схема эксперимента представлена на рис. В ходе эксперимента модель нагружалась распределенным давлением 0,3 Па, сосредоточенной силой - 3 кг, сосредоточенным моментом - 5кг?см. По измеренным деформациям были пересчитаны температурные напряжения. Графическое распределение температурных напряжений представлено на рис. 15.

Рис. 14. Экспериментальная модель и схема нагружения


Рис.15. Температурные напряжения при моделировании узких тоннельных вырезов
а Установлено, что радиальное расположение выреза, имитирующего теоретическую трещину увеличивает термонапряженное состояние исследуемого объекта, чем кольцевое. Такой результат можно использовать при проектировании изделий специального назначения атомной техники, когда капсулы с ядерным топливом в корпусах лучше располагать в кольцевом направлении.
Приведено экспериментальное моделирование термонапряженного состояния барабана теплозамедлителя, перфорированного отверстиями и имеющего геометрические неоднородности в виде разной толщины стенки. Эскизы барабана замедлителя и его модели приведены на рис. 16.
Барабан замедлителя
|
Аналоговая модель
Схема нагружения
|
Рис. 16. Экспериментальное моделирование температурных напряжений
ав барабане замедлителя
а Нагружение модели проводилось распределенной нагрузкой (р = 10кг) в виде металлической дроби и сосредоточенными моментами, приложенными к контуру невесомых включений для соблюдения условий Митчелла (М = 5кгсм). Распределение температурных напряжений в сечении исследуемого объекта приведено на рис. 17.
Выявлено, что максимальный уровень термонапряжений имеется в тонкой стенке внешнего диаметра изделия. Предложено заменить трехсвязную область сечения двухсвязной путем нанесения разрезов в тонких частях конструкции, тем самым, снижая уровень термонапряжений в три раза (рис. 18).

Рис. 17. Распределение температурных напряжений в сечении барабана замедлителя
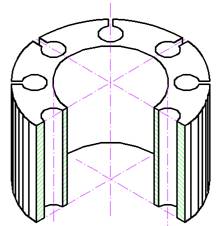
Рис. 18. Практические рекомендации для снижения уровня максимальных температурных напряжений
аа Результаты экспериментального исследования термоупругой задачи дают картину термоупругого деформированного состояния исследуемого объекта. Это свидетельствует о едином подходе при моделировании внутренних температурных напряжений в различных технических системах. Функциональное назначение системы определяет лишь значение исходных характеристик: свойства материала, параметры эксплуатации и геометрическая форма. Основу единого подхода при моделировании температурных напряжений в различных технических приложениях составляют математические аналогии в механике деформируемого твердого тела, а их сочетание является экспериментальной реализацией термомеханических аналогий.
ОСНОВНЫЕ ВЫВОДЫ
1. Разработан, математически обоснован и экспериментально реализован метод определения внутренних температурных напряжений в неоднородных элементах машиностроительных конструкций с объемным тепловыделением. Основу метода составляют математические аналогии механики деформируемого твёрдого тела, которые позволяют переходить при решении исходной задачи к другой с иным физическим содержанием, но допускающую экспериментальную реализацию моделирования термонапряженного состояния исследуемых конструкций, с учетом физических и геометрических особенностей.
2. Разработаны новые адекватные математические модели исследуемых объектов с учетом физико-механических и геометрических неоднородностей, позволяющие определять внутренние температурные напряжения в элементах конструкций с объемным тепловыделением расчетно-экспериментальными методами.
3. Получено точное аналитическое решение задачи распределения температурных напряжений в тепловыделяющих элементах сферической, цилиндрической и эллиптической форм. Установлено, что термонапряжения на поверхности цилиндрического ТВЭЛа являются растягивающими, и при прочих равных условиях их величина превышает соответствующее значение для шарового ТВЭЛа.
4. Проведен сравнительный анализ термонапряженного состояния в стержневых тепловыделяющих элементах с круговым и эллиптическим поперечными сечениями на основе решения плоской задачи термоупругости. Получено точное аналитическое решение определения температурных напряжений в цилиндрических координатах. Установлено, что уровень возникающих термонапряжений зависит от геометрической формы твэла.
5. Теоретически обоснован аналоговый метод определения температурных напряжений в элементах конструкций с переменными характеристиками, к которым относятся свойства материала, геометрическая форма и параметры эксплуатации. Его основу составляют математические аналогии механики деформируемого твердого тела.
6. Проведен сравнительный анализ термонапряженного состояния сплошного тепловыделяющего цилиндра с учетом и без учета координатной зависимости коэффициента линейного расширения и мощности объемного тепловыделения. Установлено, что при прочих равных условиях переменные характеристики изделий приводят к снижению среднего уровня термонапряжений примерно в два раза. Показана принципиальная возможность управления термонапряженным состоянием изделий путем изменения указанных характеристик.
7. Получены точные аналитические решения определения температурных напряжений в элементах конструкций односвязной области с заданными параболическими зависимостями изменения коэффициента линейного расширения и мощности объемного расширения, которые могут быть использованы в виде тестовых примеров в экспериментальной реализации метода термомеханической аналогии.
8. Приведено теоретическое обоснование метода термомеханических аналогий, основанного на решении несвязанной задачи термоупругости в квазистатической постановке, когда известное распределение температур в исследуемых объектах при соблюдении соответствующих граничных условиях позволяет определить компоненты вектора смещения.
9. Разработана и реализована методика экспериментального моделирования термонапряженного состояния отливок оболочечного типа. Выявлена закономерность появления температурных напряжений в элементах конструкций, имеющих геометрические особенности в виде отверстий и вырезов. Установлено, что несимметричное расположение отверстий существенно влияет на распределение полей деформаций и термонапряжений. Показана возможность регулирования уровня термонапряжений путем изменения конструктивных характеристик с целью повышения качества литых изделий.
10. Разработаны универсальная методика, измерительная аппаратура, нагрузочные устройства и приспособления для проведения экспериментальных работ при моделировании термонапряженного состояния элементов конструкций стержневой геометрической формы с произвольным поперечным сечением, как для односвязной, так и для многосвязных областей. Основу экспериментального моделирования составляет метод термомеханической аналогии.
11. Проведены лабораторные исследования и определены температурные напряжения в выбранных конструктивных схемах изделий атомной техники и крупногабаритных строительных конструкций. Моделирование температурных воздействий осуществлено нагружением экспериментальных моделей эквивалентными механическими нагрузками и измерением деформаций, которые затем пересчитаны в температурные напряжения. Выявленные закономерности распределения полей деформаций и термонапряжений позволяют еще на стадии проектирования изделий выявлять опасные сечения. Даны практические рекомендации к снижению максимальных уровней термонапряжений путем изменения геометрических, физико-механических и эксплуатационных характеристик.
12. Достоверность полученных результатов обеспечивается тщательным выбором устройств нагружения и инструментальных средств измерения параметров, использованием автоматических систем контроля и управления в процессе проведения эксперимента. Приведены тестовые примеры на основе точных аналитических решений задач термоупругости и теории пластин.
13. На основе разработанного расчетно-экспериментального метода определения внутренних температурных напряжений исследован и решен ряд актуальных задач механики деформируемого твердого тела. Основные результаты и рекомендации настоящей работы позволили повысить прочностную надежность проектируемых и эксплуатируемых элементов конструкций атомной техники, литейного производства и крупногабаритных строительных сооружений, что подтверждено соответствующими актами внедрения.
14. Результаты настоящего исследования в сочетании с аналитическими методами определения внутренних температурных напряжений и экспериментальным моделированием термонапряженного состояния исследуемого объекта позволяют практически реализовать математические аналогии в механике деформируемого тела. Такой подход получил развитие в экспериментальной реализации метода термомеханических аналогий.
Полученные в диссертации научные и практические результаты можно квалифицировать как решение научной проблемы определения термонапряженного состояния в неоднородных элементах машиностроительных конструкций с объемным тепловыделением на основе теоретически обоснованного и экспериментально реализованного метода термомеханических аналогий, что позволило выработать инженерно- технические решения в обеспечении прочностной надежности и безопасности эксплуатации изделий атомной техники, металлургического производства, внедрение которых вносит значительный вклад в развитие экономики страны и создания конкурентоспособной современной техники.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ ИЗЛОЖЕНЫ В СЛЕДУЮЩИХ ПУБЛИКАЦИЯХ
1. Иванов А.С. Обоснование использования пластиночной аналогии для определения термических напряжений в телах с трещинами. - Проблемы машиностроения и автоматизации. №1, 2000, с.88-89 (Перечень ВАК РФ).
2. Пахомов А.М., Иванов А.С., Никулин А.А., Савельев В.В. Моделирование термонапряженного состояния изделий с переменным модулем упругости. - Проблемы машиностроения и автоматизации. №4, 2000, с.53-56 (Перечень ВАК РФ).
3. Иванов А.С., Пахомов А.М., Никулин А.А., Булычев А.А.Определение технологических температурных напряжений в керамических изделиях, ослабленных вырезами различной формы. - Проблемы машиностроения и автоматизации. №1, 2001, с. 53-56 (Перечень ВАК РФ).
4. Никулин А.А., Иванов А.С., Гудыно Д.А., Гизатулин Н.Г. Определение термонапряженного состояния с учетом различного расположения макротрещин в поперечном сечении исследуемых стержней. - Проблемы машиностроения и автоматизации. №4, 2001, с.41Ц45 (Перечень ВАК РФ).
5. Мельников А.М., Иванов А.С., Гаврушко М.Ю. Выбор режима термообработки в зависимости от вязкопластично-упругого состояния жаропрочных тугоплавких отливок. - Проблемы машиностроения и автоматизации. №2, 2006, с.99-102 (Перечень ВАК РФ).
6. Миронова Л.И., Иванов А.С. Расчет температурного поля формообразующих частей прессформ в процессе формования литой заготовки. - Проблемы машиностроения и автоматизации. №1, 2007, с. 110-114 (Перечень ВАК РФ).
7. Миронова Л.И., Иванов А.С., Ковалев В.И. Оценка тепловых условий и термических напряжений затвердевания заготовки. - Проблемы машиностроения и автоматизации. №3, 2007, с.75-77 (Перечень ВАК РФ).
8. Иванов А.С., Ковалев В.И., Цаповская О.А. Температурные напряжения в сплошном длинном цилиндре с переменным объемным тепловыделением. - Проблемы машиностроения и автоматизации. №1, 2008, с.111-114 (Перечень ВАК РФ).
9. Чернышев Г.Н., Иванов А.С. Основы моделирования упругой пространственной среды. - Проблемы машиностроения и автоматизации. №4, 2008, с. 65-69 (Перечень ВАК РФ).
10. Иванов А.С., Цаповская О.А., Челяпина О.И. Моделирование внутренних напряжений при фазовых превращениях. - Проблемы машиностроения и автоматизации. №1, 2009 (Перечень ВАК РФ).
11. Иванов А.С. Математические аналогии в термомеханике. - Обозрение прикладной и промышленной математики. Том 16, выпуск 5, 2009, с.648-649 (Перечень ВАК РФ).
12. Миронова Л.И., Иванов А.С. К вопросу о выборе оптимальных размеров элементов конструкций форм литья. - Проблемы машиностроения и автоматизации. №2, 2009, с.70-73 (Перечень ВАК РФ).
13. Иванов А.С., Миронова Л.И. Моделирование температурного изгиба пластины. - Обозрение прикладной и промышленной математики. Том 16, выпуск 2, 2009, с.1069-1070 (Перечень ВАК РФ).
14. Иванов А.С. Моделирование внутренних напряжений в элементах конструкций с переменными физико-механическими свойствами. - Проблемы машиностроения и автоматизации. №4, 2009, с.116-117 (Перечень ВАК РФ).
15. Иванов А.С., Миронова Л.И. Математическое обоснование эксперимента для определения функции напряжений в плоской задаче термоупругости. - Обозрение прикладной и промышленной математики. Том 17, выпуск 2, 2010, с.268-269 (Перечень ВАК РФ).
16. Иванов А.С. Температурные напряжения при изменении формы тепловыделяющих элементов. - Проблемы машиностроения и автоматизации. №2, 2010, с.97-100 (Перечень ВАК РФ).
17. Иванов А.С., Ковалёв В.И., Челяпина О.И. Тестовые примеры при моделировании температурных напряжений в элементах конструкций с переменными характеристиками. - Обозрение прикладной и промышленной математики. Том 17, выпуск 3, 2010, с.410-411 (Перечень ВАК РФ).
18. Иванов А.С., Миронова Л.И., Челяпина О.И. Математические аналогии для определения внутренних напряжений в плоской задаче термоупругости. - Обозрение прикладной и промышленной математики. Том 17, выпуск 4, 2010, с.558-559 (Перечень ВАК РФ).
19. Иванов А.С. Внутренние напряжения в прикладных задачах механики деформируемого твердого тела. - Проблемы машиностроения и автоматизации. №3, 2010, с.94-96 (Перечень ВАК РФ).
21. Иванов А.С. температурные напряжения при изменении сферической формы тепловыделяющих элементов. - Проблемы машиностроения и автоматизации. №1, 2011, с.110-112 (Перечень ВАК РФ).
22. Иванов А.С. Моделирование температурных напряжений в элементах конструкций с учетом переменных теплофизических свойств материала. - Обозрение прикладной и промышленной математики. Том 18, 2011 (Перечень ВАК РФ).
23. Иванов А.С. Тестовые примеры при моделировании внутренних напряжений в изделиях с неоднородной структурой материала. - Проблемы машиностроения и автоматизации. №3, 2011, с.107-110 (Перечень ВАК РФ).
24. Доброславский А.В., Иванов А.С., Савельев В.В. Исследование процесса остывания отливки в условиях свободного теплообмена с окружающей средой. ТрудыVII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2000 с.116-120.
25. Доброславский А.В., Иванов А.С., Савельев В.В. Исследование нестандартного поля напряжений в отливке с трещиной. Труды VII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2000 с.120-125.
26. Доброславский А.В., Иванов А.С. Исследование стационарных полей температур и напряжений в тепловыделяющем цилиндре с туннельными разрезами. Труды VII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2000 с.177-181.
27. Иванов А.С., Гизатулин Н.Г. Температурные напряжения в тепловыделяющих элементах с учетом микротрещин. Труды VII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2000 с.181-195.
28. Иванов А.С., Егоров П.Е., Старостин С.А. Выбор геометрии крышки графитовой. Труды VII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2000 с.204-207.
29. Пашуков С.А., Иванов А.С. Дифференциальный шариковый фрикционный вариатор. Труды XI международного семинара Технологические проблемы прочности. Москва, МГОУ, 2004, с.199-208.
30. Толкачев В.М. Мельников А.М., Иванов А.С. Идея трехточечного опорного контура. Труды XI международного семинара Технологические проблемы прочности. Москва, МГОУ, 2004, с.109-116.
31. Рыков Ю.М., Толкачев В.М., Иванов А.С. Температурный изгиб пластин по цилиндрической поверхности. Труды XI международного семинара Технологические проблемы прочности. Москва, МГОУ, 2004, с.125-135.
32. Иванов А.С. Критерии предельных напряженных состояний конструкционных материалов. Учебно-методическое пособие. Москва, МГОУ, 2005, 79 с.
33. Тараторин Б.И., Иванов А.С., Гаврушко М.Ю. Сопротивление хрупких материалов разрушению. Труды XIII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2006, с.189-193.
34. Иванов А.С., Мельников А.М., Гаврушко М.Ю. Определение температурных напряжений оболочек сложного очертания. Труды XIII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2006, с.244-246.
35. Иванов А.С. Определение термопрочности керамических изделий на основе их предельных состояний. Монография, Москва, МГОУ, 2007, 190с.
36. Иванов А.С., Миронова Л.И., Ковалев В.И. Оценка температурного поля заготовки. Труды XIV международного семинара Технологические проблемы прочности. Москва, МГОУ, 2007,с.151-159.
37. Иванов А.С., Мельник М.В., Ковалев В.И. Классические теории прочности и области их применения и ограничения. Труды XIV международного семинара Технологические проблемы прочности. Москва, МГОУ, 2007,с.68-74.
38. Иванов А.С., Цаповская О.А. Влияние формы тепловыделяющих элементов на уровень и характер распределения температурных напряжений. Труды XV международного семинара Технологические проблемы прочности. Москва, МГОУ, 2008,с.65-72.
39. Иванов А.С., Куликов В.Г., Гаврушко М.Ю. Определение температурных напряжений в реакторах с помощью статико-геометрической аналогии. Труды XV международного семинара Технологические проблемы прочности. Москва, МГОУ, 2008,с.73-85.
40. Иванов А.С. Внутренние напряжения при фазовых превращениях. Труды XVI международного семинара Технологические проблемы прочности. Москва, МГОУ, 2009,с.113-118.
41. Иванов А.С. Математические аналогии в механике сплошной среды. Монография. Москва, МГОУ, 2009, 180с.
42. Иванов А.С., Миронова Л.И. Особенности разрушения биметаллических элементов конструкций. Сборник материалов ХХ Петербургские чтения по проблемам прочности. Санкт-Петербург, 2010, с.186-188.
43. Иванов А.С. Экспериментальная реализация термомеханических аналогий в механике деформируемого твердого тела. Труды XVII международного семинара Технологические проблемы прочности. Москва, МГОУ, 2010,с.12-13.

Усл. печ. л. 2,7. аТираж 100 экз. Заказ №202К.
Издательство Московского государственного открытого
Университета им. В.С. Черномырдина.
107996, Москва, ул. Павла Корчагина, д.22.
Типография МГОУ
а
 Все авторефераты докторских диссертаций
Все авторефераты докторских диссертаций