Авторефераты по всем темам  >>  Авторефераты по экономике

Моделирование процессов управления рыночным равновесием с применением нечетко-возможностных математических методов

Автореферат докторской диссертации по экономике

 

а На правах рукописи

 

РАДИОНОВ Николай Васильевич

 

 

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ

РЫНОЧНЫМ РАВНОВЕСИЕМ

С ПРИМЕНЕНИЕМ НЕЧЕТКО-ВОЗМОЖНОСТНЫХ

МАТЕМАТИЧЕСКИХ МЕТОДОВ

 

Специальность 08.00.13 - Математические

и инструментальные методы экономики

 

 

 

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора экономических наук

 

 

 

 

 

Санкт-Петербург - 2011

Работа выполнена в Государственном образовательном учреждении высшего профессионального образования "Санкт-Петербургский государственный университет экономики и финансов"

доктор экономических наук, профессор

Соколов Дмитрий Викторович

а 

Научный консультант Ца

доктор экономических наук, профессор

Давнис Валерий Владимирович

а 

Официальные оппоненты:

доктор экономических наук, профессор

Торопцев Евгений Львович

ааа

доктор технических наук, профессор

Бурлов Вячеслав Георгиевич

аа

 

а

Федеральное государственное образовательное учреждение высшего профессионального образования "Санкт-Петербургский государственный университет"

а 

Ведущая организация -

 

 

Защита состоится "_10_" ____марта____ 2011 года в ____ часов на заседании диссертационного совета Д 212.237.03 при Государственном образовательном учреждении высшего профессионального образования "Санкт-Петербургский государственный университет экономики и финансов" по адресу: 191023, Санкт-Петербург, ул. Садовая, 21, ауд. ______.

а

С диссертацией можно ознакомиться в библиотеке Государственного образовательного учреждении высшего профессионального образования "Санкт-Петербургский государственный университет экономики и финансов"

а

Автореферат разослан "____" ____________ 2011 года

а

Ученый секретарь диссертационного совета

А. В. Завгородняя

а 

 

 

 

 

 

 

 

 

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы исследования. В современной макроэкономической теории, базирующейся в основном на фактах реальной экономической жизни, при исследовании процессов формирования совокупного спроса и предложения прочно утвердился системно-научный или модельный подход к решению важнейшей задачи экономики - согласованию ограниченных производственных возможностей и неограниченных потребностей людей. Логическим следствием применения такого подхода явилась возможность предвидеть развитие исследуемых процессов и оценивать возможный результат, исходя из известных условий и логики поведения элементов экономической системы.

Растущая глобализация экономики, которая наблюдалась всю вторую половину ХХ века, вместе с углубленными исследованиями и обобщением базовых макроэкономических моделей классической и кейнсианской школ, накоплением эмпирических данных и охватом макроэкономической теорией новых сфер экономической жизни - все это постепенно формирует новый взгляд на роль макроэкономики в российской экономической науке. В настоящее время макроэкономическая теория становится одним из важнейших инструментов в процессе принятия не только национальных и глобальных (макроуровень), но и региональных (мезоуровень) и даже локальных (микроуровень) социально-экономических решений. Эти тенденции привели к серьезному теоретическому переосмыслению требований к макроэкономическим моделям.

Очевидно, что, независимо от формы описания модели, результативность модельного подхода зависит от степени адекватности отражения этим описанием реальной экономической жизни. Однако уровень соответствия наиболее распространенного математического инструментария (в основном детерминированного концептуального или графо-аналитического) новым требованиям к современным макроэкономическим моделям остается весьма низким. Даже учет "поведенческого аспекта" в теоретической макроэкономике, с помощью которого был достигнут значительный прогресс в описании теории общего равновесия, лишь частично решает проблему адекватности.

Следует отметить, что современная рыночная экономика относится к классу смешанных. В ней производство развивается под воздействием собственных рыночных эффектов, вызывающих, зачастую, не вполне логически обоснованную потребительскую активность домашних хозяйств. При этом государство регулирует этот процесс: устанавливает правовую структуру бизнеса и контролирует ее соблюдение, опираясь на данные статистики производства и потребления, обычно имеющей аслучайный характер. Макроэкономическая модель такой экономики должна представлять собой сложнейший аппарат, в частности учитывающий и разнообразные описания неопределенности рыночного и государственного, внутреннего и внешнего регулирования. Однако, в отличие от естественных наук (физика, химия и др.), в экономике возможности проведения "натурных" экспериментов весьма ограничены. Поэтому применение традиционного вероятностно-статистического модельного подхода, требующего многократности и повторяемости в одинаковых условиях явлений экономической жизни, часто оказывается малопродуктивным или вовсе невозможным. Совершенствование этого аппарата прежде всего нуждается в тех идеях и тех подходах, с помощью которых можно реализовать математическую методологию, более полно учитывающую "поведенческие" аспекты при описании процессов развития рыночной экономики в кризисных и переходных условиях. Это позволит получить сбалансированные соотношения в макроэкономических моделях, учитывающих не только агрегированные слабо управляемые процессы установления равновесных состояний, но и субъективные факторы, отражающие возможное, полезное или наиболее достоверное и приемлемое при данной информации поведение экономических агентов.

Следует также отметить, что практическая ценность традиционных стохастических и оптимизационных макроэкономических моделей из-за вынужденного упрощения становится сомнительной. В то же самое время имитационные модели выполняют роль инструмента для решения сложных практических (микроэкономических) проблем, но не могут служить основой для решения задач макроэкономического характера. Таким образом, возникает противоречие, разрешение которого может способствовать формированию нового взгляда на основополагающие концепции макроэкономических теоретических исследований с учетом многообразия и скорости изменения экономической действительности и привлечения аппарата как микро, так и макроэкономического моделирования, за счет чего может быть расширена аксиоматика и обеспечена полнота макроэкономических моделей. а

Предлагаемый в диссертации подход к усовершенствованию математических макроэкономических моделей основан на использовании молодого и бурно развивающегося направления математики - нечеткой математики. Рамки данного исследования требуют актуализации основных вопросов, связанных с: 1) выявлением и обобщением причин неустойчивости детерминированных результатов базовых моделей классической и кейнсианской школ относительно правдоподобных вариаций исходных предпосылок; 2) корректным применением теории нечеткой меры ав азадачах аобработки арыночной информации, апредставленной ав авиде анечеткого множества, отношения, отображения и развитием на этой основе методов нечеткого макроэкономического анализа; 3) разработкой методов прогнозирования и обоснования решений по управлению национальной экономической системой в целях обеспечения долгосрочного поддержания равновесия рыночной экономики в современных геополитических и экономических условиях.

Степень разработанности проблемы. Несмотря на достаточно длительную историю развития самой макроэкономической теории, ее прочные математические основы были заложены только в ХХ веке классическими фундаментальными исследованиями А. Маршалла, Дж. М. Кейнса, В. Леонтьева, М. Самуэльсона и других. Эти исследования привели к обоснованию основных детерминированных макроэкономических моделей: классических моделей круговых потоков, моделей AD-AS и IS-LM, кривых О. Филипса и А. Лаффера, "креста" Дж. Кейнса, моделей экономического роста Р. Солоу, моделей Т. Сарджента, Р. Лукаса, Н. Уоллеса, Дж. фон Неймана, моделей конкурентной экономики К. Эрроу, Ж. Дебре и других. Однако, еще в середине XX века макроэкономические модели формулировались в основном в концептуальной форме, так как постулат эмерджентности функционирования экономики делал бессмысленным формальное описание целей и критериев этого функционирования. Примером могут служить концептуально противоположные модели, известные лишь как закон Сэя и "парадокс сбережений" Кейнса. Выдвинутые в дальнейшем идеи послужили основой для развития двух противоположных концептуальных макроэкономических моделей - классической и кейнсианской.

Базой классического направления явились работы К. Маркса, Л. Вальраса, Ж.-Б. Сэя, В. Парето, А. Маршалла, экономистов "кембриджской школы" и других. Изложенные в этих работах важнейшие концептуальные постулаты позволили экономистам ХХ века получить четко формализованные макроэкономические модели, в определенной степени обобщающие микроэкономический закон спроса и предложения. Учитывая, что классический подход использует в качестве параметров моделей измеримые и наблюдаемые величины, можно говорить о детерминированности и объективности такого подхода.

Основным постулатом "Общей теорииЕ" Кейнса явилось утверждение о большей жесткости заработной платы по сравнению с ценами. Вначале это привело к полному отказу от классической концепции и модели несовершенной конкуренции с полностью жесткими ценами и заработными платами. Наиболее логичным кейнсианская модель IS-LM связи выглядит в известной интерпретации Дж. Хикса. Появление кейнсианства существенно поколебало позиции классической макроэкономики и макроэкономика в данном направлении постоянно развивалась всю вторую половину ХХ века, трансформируясь в неоклассическую концепцию рациональных ожиданий Р. Лукаса. При условии абсолютно гибких цен и ставок процента экономика рациональных ожиданий становится устойчивой при любых возмущениях денежной массы (саморегулируемой при совершенной конкуренции). Это, в свою очередь, привело к модели с полной независимостью реального рынка от рынка денег (классическая дихотомия), либо к модели с аукционером рынка, который ликвидирует неравновесие, возникающее за счет эффекта реальных денежных остатков (неоклассическая неправильная дихотомия).

Идеи и методические приемы классического и неоклассического направлений макроэкономической теории были использованы при построении экономико-математических моделей с использованием аппарата линейного динамического прогнозирования и стационарных случайных процессов. Исследованиям возможностей применения этого аппарата посвящены работы А. Г. Аганбегяна, А. Г. Гранберга, Г. Б. Клейнера, В. Л. Макарова, Н. Н. Моисеева, В. С. Немчинова, В. В. Новожилова, Н. Я. Петракова, В. М. Полтеровича, В. Л. Рубинова, Ю. Н. Черемных и других. Большой вклад в разработку макроэкономических моделей, ориентированных на статистический подход к описанию экономических процессов, был сделан С. А. Айвазяном, Дж. Боксом, С. В. Вишневым, П. А. Ватником, Дж. Джонстоном, Г. Дженкинсом, Н. К. Дружининым, И. И. Елисеевой, М. Дж. Кендаллом, Э. К. Маленво, П. Ньюболдом, С. А. Саркисяном, А. Стюартом, Г. Тейлом, Я. Тинбергеном, Г. Тинтнером, Е. М. Четыркиным и другими.

Особое значение в развитии макроэкономики сыграл переход от концептуальных статических к математическим динамическим моделям с учетом анализа характера поведения экономических субъектов. Большую роль в выявлении таких закономерностей внесло внедрение в макроэкономику методов кибернетики и системного анализа. Развитию этого направления в технической области было посвящено особенно много работ в момент зарождения направления в 50-70х годах ХХ века. Однако в последующем многие системно-кибернетические идеи были применены и в области микро- и макроэкономики. Особую роль в широком внедрении кибернетических методов в экономические исследования сыграли работы И. М. Сыроежина. В дальнейшем прикладные исследования в этом направлении были развиты в работах А. В. Воронцовского, В. М. Гальперина, О. Г. Голиченко, аП. И. Гребенникова, А. И. Леусского, А. В. Луссе, И. В. Лысенко, Ю. А. Львова, А. Н. Миронова С. Г. Светунькова, Д. В. Соколова, Б. А. Резникова, Л. С. Тарасевича, В. П. Чернова и других, что свидетельствует об актуальности постоянного поиска новых подходов в математической макроэкономике.

Постоянный интерес вызывают также вопросы применения вероятностных и статистических методов в макроэкономическом моделировании. Теоретической базой этого направления стали результаты фундаментальных исследований Р. Беллмана, Е. С. Вентцель, Л. Заде, А. Н. Колмогорова, М. Миллера, Ф. Модильяни, Дж. Саридиса, У. Шарпа, Я. З. Цыпкина и других. Однако, зачастую, эти результаты либо развивали только математическую теорию, либо предназначались для решения только технических задач. Экономическое направление в большинстве этих работ охватывало лишь частные примеры, отдельные секторы экономики или отдельные рынки, что не позволяло корректно распространить полученные результаты в целом на макроэкономическое моделирование.

В последнее время большое развитие получило направление адаптивного прогнозирования экономических явлений, реализующее подход совместного использования адаптивных принципов и методов имитационного моделирования. В рамках этих моделей впервые была поставлена проблема комбинирования стохастических и субъективных оценок. Новейшие разработки в области адаптивного моделирования опираются не только на априорные зависимости между макропеременными, но и на поведенческие модели агентов и теорию общего равновесия. Исследование экономического прогнозирования на принципах адаптации было начато Р. Брауном, П. Винтерсом, К. Негойцэ, И. И. Перельманом, Ч. Хольтом, Р. Ягером и продолжено В. П. Бородюком, В. Г. Бурловым, В. В. Давнисом, Е. М. Левицким, А. И. Орловым, П. В. Севастьяновым, Д. П. Севастьяновым, Г. Б. Шильманом, Е. Л. Торопцевым, Ю. Н. Эйсснером и другими.

Несмотря на достигнутые значительные успехи, в развитии макроэкономической теории на современном этапе прослеживаются две характерные негативные тенденции, указанные, например, в работах В. М. Полтеровича:

• Большинство детерминированных и стохастических результатов неустойчивы относительно правдоподобных вариаций исходных предпосылок.
• Обнаруженные эмпирические закономерности не накапливаются, а, напротив, опровергаются последующими исследованиями.

Преодоление первой тенденции, как правило, связано с применением все более и более сложных методов динамического моделирования, в том числе, с использованием принципа Р. Бира включения "черного ящика" того или иного "оттенка" в цепь управления.

Идеи преодоления второй тенденции развиваются на основе учета особого свойства активности экономических систем. В таких системах принятие окончательных решений принадлежит только человеку, а не машине, какой бы совершенный алгоритм в нее не был заложен. Именно в рамках этого направления в последнее время идет бурное развитие методов комплексного адаптивного прогнозирования и построения адаптивно-имитационных моделей. В частности, разработке этого направления посвящены труды В. В. Давниса, Е. М. Левицкого и других.

Однако, применительно к макроэкономическим моделям, идеи создания математического аппарата, обладающего высокой степенью адекватности, не в полной мере учитывали двойственность самого свойства активности макроэкономических систем. Так, с одной стороны, при самой высокой степени адекватности a-posteriori, существенно снижается правдоподобность оценок с использованием аппарата динамического прогнозирования. С другой стороны, использование только субъективных оценок a-priori ограничивает математический аппарат лишь до уровня графо-аналитических малоразмерных и качественных моделей.

К сожалению, идеи комбинирования экстраполяционных и субъективных оценок пока что ограничиваются рамками адаптивно-рациональных моделей микроэкономики (отдельных процессов, в лучшем случае - рынков) и используют лишь один (либо поссибилический, либо аксиологический) аспект двойственности в моделях выбора экономических агентов.а аа

В настоящее время известно достаточно ограниченное количество исследований в данной области. Анализ результатов этих исследований, проведенный, например, в работах Дж. Армстронга, И. Махуда, А. О. Недосекина, В. И. Тиняковой, показал, что в основном они относятся к начальному уровню понимания и разработки проблемы учета двойственности в экономических системах при макроэкономическом моделировании. В них явно преобладает поисковый характер, что и выводит на первый план проблему построения адекватных моделей рыночной экономики с применением нечетко-возможностных математических методов для учета двойственности свойства активности макроэкономических систем.а

Объект исследования - рыночный механизм установления общего равновесия в экономической системе на макро- и мезоуровне .

Предмет исследования - современный аппарат моделирования процессов установления и поддержания общего экономического равновесия и возможности его применения.

Цель исследования - развитие аппарата макроэкономического моделирования с использованием нечетко-возможностных математических методов анализа микроэкономических процессов, моделирования мотивации фирм, домашних хозяйств и механизмов уравновешивания спроса и предложения, расширяющих прикладные возможности современной макроэкономики.аа

Анализ условий достижения этой цели показал необходимость решения нескольких взаимосвязанных задач в следующей постановке:

• Выявить основные проблемы повышения адекватности моделей и методов макроэкономического моделирования и разработать концепцию нечеткого макроэкономического моделирования, учитывающую экономико-математическую формализацию понятий возможности и полезности в описаниях закономерностей макроэкономических взаимосвязей.
• Разработать средства макроэкономического моделирования, прикладные возможности которых ориентированы на широкое применение нечетко-возможностного математического аппарата для описания неопределенности макроэкономических взаимосвязей:
• в случае моделирования мотивации рыночного поведения основных макроэкономических агентов;
• в случае моделирования рыночных процессов установления общего экономического равновесия.
• Исследовать возможности применения инструментария нечеткой алгебры для расчетов:
• в макроэкономических моделях произвольной линейно-аддитивной структуры;
• в макроэкономических моделях с нечеткой мерой.
• Исследовать прикладные аспекты нечетко-возможностного подхода в целях повышения адекватности описания макроэкономических явлений в условиях неопределенности в случае:
• инейных динамических макроэкономических моделей экономического роста;
• агрегированных динамических макроэкономических моделей;
• моделей установления рыночной стоимости фирм.
• Разработать методическое обеспечение для решения макроэкономических задач с применением нечетко-возможностного математического инструментария:
• задач выбора структуры акционерного капитала при наличии нечеткой информации о доходности ценных бумаг (теория Миллера-Модильяни);
• задач линейного лингвистического распознавания состояния экономических агентов при нечетком описании финансово-экономических параметров.

Область исследования. Содержание диссертации соответствует п.1.2 Теория и методология экономико-математического моделирования, исследование его возможностей и диапазонов применения: теоретические и методологические вопросы отображения социально-экономических процессов и систем в виде математических, информационных и компьютерных моделей специальности 08.00.13 - Математические и инструментальные методы экономики - паспорта специальности ВАК РФ.

Теоретической и методологической основой исследованияа послужили современные достижения экономической и математической наук, содержащиеся в трудах отечественных и зарубежных ученых по макроэкономике, экономической динамике, теории фондовых и финансовых рынков, менеджменту, теории фирмы, теории систем, исследованию операций, теории вероятностей, теории нечетких множеств, теории возможностей, эконометрическому моделированию, экспертному оцениванию.

Эмпирическую базу исследования составили:

• данные, опубликованные Федеральной службой государственной статистики, а также Территориальным органом Федеральной службы государственной статистики по Санкт-Петербургу и Ленинградской области;
• данные, предоставленные аналитическим информационным центром (АИЦ) при Администрации Санкт-Петербурга, Комитетом по экономическому развитию Санкт-Петербурга;
• архивы фондовой информации российских компаний, размещенные на сайтах Российской торговой системы (

Научная новизна исследования состоит в разработке и реализации концепции анализа макроэкономических процессов и создания макроэкономических моделей на основе применения нечетко-возможностной математической методологии, позволяющей более полно учитывать "поведенческие" аспекты при описании процессов развития рыночной экономики в различных условиях. В отличие от существующих подходов, предложенный подход позволяет получать такие сбалансированные соотношения в макроэкономических моделях, которые учитывают не только агрегированные слабо управляемые процессы установления равновесных состояний, но и субъективные факторы, отражающие возможное, наиболее достоверное, либо полезное при данной информации поведение экономических субъектов. Построенные в рамках такой концепции макроэкономические модели дают наиболее полное и адекватное представление об ожидаемых вариантах макроэкономических взаимосвязей и предпочтительных решениях по обеспечению и поддержанию общего экономического равновесия.

Научная новизна разработанной концепции и подхода к ее реализации заключается в следующих результатах, полученных лично автором:

1. Проведено теоретическое обоснование подхода к макроэкономическому моделированию процессов установления и поддержания общего экономического равновесия с широким учетом факторов субъективной неопределенности, описываемой нечеткими множествами. Это закладывает экономико-математическую основу для наиболее полного учета поведенческого аспекта при описании процессов в рыночной экономике. Предложенный подход позволяет получать сбалансированные соотношения в макроэкономических моделях, учитывающих не только агрегированные слабо управляемые процессы установления равновесных состояний, но и субъективные факторы, отражающие возможное, полезное или наиболее достоверное и приемлемое при данной информации поведение экономических агентов.

2. Предложены основные направления реализации методов моделирования мотивации экономических агентов, учитывающие различные факторы неопределенности при решении задач оптимального выбора.

3. Разработан новый подход к использованию неаддитивной нечеткой меры при оценивании субъективного аспекта в экономических моделях. Это позволяет согласовывать процедуры обработки информации с особенностями человеческого мышления.

4. Предложены новые методики обработки информации о рыночной статике и динамике, представленной в виде нечеткого множества, отношения, отображения, позволяющие развивать на этой основе методы нечеткого макроэкономического анализа.

5. На основе использования неаддитивной нечеткой меры обоснованы решения по анализу, прогнозированию и управлению экономической системой на макро или мезоуровне, реализация которых обеспечит долгосрочное поддержание равновесия рыночной экономики.

6. Разработана методическая база логико-алгебраических вычислений в экономических моделях с нечеткими параметрами на основе нечетких бинарных алгебраических операций, заданных на базовых множествах линейными уровневыми функциями аргументов. На примерах нескольких наиболее распространенных функций транзитивной смеси типа функций "пессимистического оптимиста" или мини-максных смесей показано, что "свертка" цепочки высказываний макроэкономического субъекта, выполняемая с целью адаптивно-рационального определения единого показателя выбора, может осуществляться аналогично выполнению нечетких арифметических операций на основе новой математической конструкции - предикатных смесей. Разработан программно-математический аппарат реализации этого подхода в макроэкономических моделях.

7. Предложен новый методический подход к обоснованию магистральных экономических моделей с применением нечетко-возможностного инструментария. Показано, что трудности, связанные с построением традиционных стохастических моделей и решением соответствующих магистральных задач в M-постановке, могут быть преодолены с использованием нечетких моделей, развиваемых в рамках той же M-постановки. Разработана концепция трансформирующего I-подхода к задаче нечеткой оптимизации, с использованием которого по аналогии со стохастическими можно сформулировать две сопряженные (прямая и "условно" двойственная) нечеткие модели в M-постановке. При этом в модели расчетных цен для однообразного применения индикатора неравенства может быть принято условие слабой эквивалентности операции отрицания нечеткого числа.

8. Проведена практическая апробация разработанной концепции на данных, отражающих динамику оценок стоимости фирм на фондовых рынках. Для этого проведено детальное рассмотрение условий и методики доказательства первой теоремы Миллера-Модильяни. Предложен новый подход к доказательству этой теоремы с использованием нечетких множеств для моделирования субъективных рыночных факторов, позволяющий преодолеть известные трудности теоретического объяснения правдоподобных отклонений статистических данных.аа а

9. Проведена практическая апробация разработанной концепции для статистики оценивания банкротств. С этой целью предложена методика решения задач линейного лингвистического распознавания состояния экономических агентов при нечетком описании финансово-экономических параметров. Верификация методики на данных РФ последних 10 лет показала, что,а в отличие от существующих методик, использующих принципы гиперплоскостного разделения данных, предложенная методика позволяет получать более надежный инструмент распознавания состояния банкротства.

Теоретическая значимость работы определяется тем, что разработанная в ней новая концепция макроэкономического моделирования процессов установления и поддержания общего экономического равновесия с широким учетом факторов субъективной неопределенности, описываемой нечеткими множествами, задает в макроэкономике новое направление комплексного использования различной информации о макроэкономических процессах.

Практическая значимость результатов исследования заключается в возможности применения разработанного научно-методического обеспечения и его математической реализации для получения ряда новых экономических и математических решений, направленных на совершенствование макроэкономических моделей. За счет этого обеспечивается повышение адекватности прогнозирования процессов в национальной или региональной экономике. Разработанный научно-методический аппарат позволяет решать разнообразные макроэкономические задачи с учетом факторов неопределенности при сохранении требуемых значений целевых характеристик макроэкономических моделей.

Свидетельством значимости результатов выполненных исследований и, одновременно, их достоверности служит тот факт, что на протяжении последних пяти лет как в Российской Федерации, так и за рубежом проводятся интенсивные исследования и разработки, направленные на внедрение методологии нечетко-возможностного моделирования различных макроэкономических процессов и систем. Самостоятельное практическое значение имеют:

макроэкономические решения:

• методика учета факторов двойственности макроэкономических явлений при разработке математического аппарата моделирования процессов установления общего экономического равновесия в целях повышения адекватности макроэкономических моделей реальным процессам в национальной экономике.
• методика макроэкономичекского моделирования с использованием линейных динамических нечетко-возможностных макроэкономических моделей открытой экономики, которые позволяют реализовать концепцию многофакторного учета неопределенности объективного и субъективного характера при моделировании экономического роста.а

математические решения:

• математический аппарат нечетких логико-алгебраических вычислений с кусочно-линейными уровневыми функциями нечетких чисел, позволяющий с заданной точностью аппроксимировать операции над нечеткими числами с произвольным описанием уровневых функций;
• математический аппарат нечетких логических операций для решения задач оптимизации, решения неравенств и распознавания при нечетком описании экономических параметров.

Апробация и внедрение результатов исследования. Основные результаты работы прошли апробацию и получили положительную оценку на семинарах в Санкт-Петербургском государственном университете экономики и финансов "Конкурентоспособность российской экономики (проблемы и перспективы)" (Санкт-Петербург, 2003), на ХIII Всероссийской научно-практической конференции в РАРАН "Актуальные проблемы защиты и безопасности" (Санкт-Петербург, 2010), на конференции в Санкт-Петербургском государственном Горном институте им. Г. В. Плеханова (техническом университете) "Устойчивое развитие отечественных компаний: проблемы, перспективы" (Санкт-Петербург, 2010), на VI Московской международной конференции по исследованию операций "ORM 2010" (Москва, 2010), на региональных и ведомственных конференциях в Санкт-Петербургском государственном университете экономики и финансов и Военно-космической академии им. А. Ф. Можайского.

Основные результаты исследования нашли отражение в учебно-методических комплексах по следующим дисциплинам, преподаваемым в Военно-космической академии им. А. Ф. Можайского: "Основы военной экономики", "Электромеханика и электропривод" (имеется акт внедрения).

Программно-методический аппарат линейного лингвистического распознавания состояния экономических агентов при нечетком описании финансово-экономических параметров реализован в НИИ-4 МО при проведении анализа экономических проблем строительства космических войск на период до 2011 г. и разработке методики определения первоначальной стоимости объектов космических войск, на которую отсутствует бухгалтерская документация (имеется акт внедрения).

Нечетко-возможностные математические модели для задач оценки финансовой реализуемости федеральных космических программ использованы при оценивании эффективности проектов модернизации и эксплуатации космической техники в условиях ограниченного финансирования в Военно-научном комитете Космических войск РФ (имеется акт внедрения).

Публикации. По теме диссертации опубликовано 27 работ (вклад автора составляет 96,1 п.л.), в том числе 3 монографии и 10 статей в научных журналах, рекомендованных ВАК РФ для публикации основных результатов диссертаций на соискание ученой степени доктора наук.а

Структура работы обусловлена целью, составом решаемых задач и логикой исследований. Диссертация состоит из введения, пяти разделов, заключения, списка литературы из более чем 300 наименований и приложений.

В первом разделе излагаются основные проблемы разработки адекватных моделей рыночной экономики. Проводится детальный анализ методологических и методических аспектов проблемы анализа макроэкономических взаимосвязей. На основе рассмотрения особенностей современной методологии макроэкономических исследований изложены общие понятия и дана классификация макроэкономических моделей, разработанных к настоящему времени. В результате анализа моделей и методов макроэкономического моделирования выявляются некоторые важные проблемы использования математической теории выбора в условиях неопределенности в макроэкономических моделях. Излагаются методологические основы современных и перспективных макроэкономических концепций. Вначале по отдельности рассматриваются основы и проблематика концепций высшего (макроэкономического) и низшего (микроэкономического) уровней. Далее, как результат композиции этих концепций, рассматривается проблематика моделей общего экономического равновесия и методология теории общественного выбора. При этом детализируется концептуальная модель общего экономического равновесия и математическая модель общественного выбора. В заключение на основании анализа существующих моделей выявляется проблематика синтеза моделей общего экономического равновесия, синтеза макроэкономических концептуальных моделей, а также проблематика исследования закономерностей макроэкономических взаимосвязей с учетом факторов неопределенности.

Во втором разделе рассмотрены нечетко-вероятностные методы исследований и глобальная проблема оценивания возможностей в задачах моделирования макроэкономики. На основании анализа экономико-математическойа методологииа моделированияа са использованием методов декомпозиции отношений, а также с использованием методов декомпозиции отображений рассматриваются подходы к формализованному представлению моделей общего экономического равновесия. Обосновывается переход от классической формализации моделей общего экономического равновесия к формализованным неоклассическим и неокейнсианским моделям, что позволяет учитывать различные факторы неопределенности и обеспечить корректность сближения микро- и макроэкономических моделей. С этой целью разрабатывается концепция нечеткой меры, а также обобщенный нечетко-возможностный подход к моделированию макроэкономики. На основе анализа категорий неопределенности, используемых при исследовании сложных систем, предлагается соответствующая математическая структура в задачах моделирования экономических систем с учетом факторов неопределенности. Анализируются основные пути и методы решения задач нечеткой оптимизации в моделях мотивации экономических субъектов.

В третьем разделе с учетом выбранных во втором разделе направлений и сформулированных требований к макроэкономическому моделированию излагаются основы создания специального математического инструментария нечеткой алгебры в целях моделирования процессов в сложных экономических системах. Для этого на основе понятия нечеткого числа и операций с нечеткими числами разрабатывается математическое описание бинарных алгебраических и логических операций с нечеткими числами. В качестве обобщения этих математических конструкций разрабатывается инструментарий нечеткой алгебры на основе предикатных смесей. При этом общие определения основных алгебраических операций на смесях конкретизируются разработкой нечетких бинарных алгебраических операций, заданных на базовых множествах линейными уровневыми функциями аргументов. Далее проводятся исследования разработанного математического инструментария. Вначале исследуется методика логико-алгебраических вычислений в экономических моделях с нечеткими параметрами. Затем анализируются основные свойства нечетких алгебраических бинарных операций.

В четвертом разделе на основе методического аппарата второго и третьего разделов рассматриваются вопросы создания линейных динамических нечетко-возможностных моделей национальной экономики. На основе анализа моделей долгосрочного планирования и прогнозирования, учитывающих динамику рыночной экономики с продолжительным временным промежутком, и моделей с использованием магистрального подхода разрабатывается динамическая модель экономики в матричной форме. Вначале в целях учета фактора двойственности в макроэкономических моделях разрабатываются динамические модели на основе простого межпроцессного обмена - динамические производственные модели и динамические стоимостные модели. Далее в целях учета факторов неопределенности разрабатывается нечетко-вероятностные магистральные модели по типу Неймана в постановке с математическим ожиданием, по типу Вальраса с учетом нечетко-возможностного разброса (аналогов дисперсии), а также динамические нечетко-возможностные межотраслевые модели. В заключение проводится анализ основных подходов к учету факторов двойственности и неопределенности в агрегированных макроэкономических динамических моделях по типу Солоу.

В пятом разделе на основе методологии, изложенной в предыдущих разделах, рассматриваются некоторые важные прикладные результаты применения нечетко-вероятностного подхода к решению макроэкономических задач. В частности, рассматривается решение задач выбора структуры акционерного капитала при наличии нечеткой информации о доходности ценных бумаг, обобщенное в теореме Миллера-Модильяни (ММ). На основе анализа классической формулировки теоремы ММ и таких факторов современной экономической действительности, как влияние индивидуальной ставки по кредитам для инвесторов и влияние различий в процентных ставках по облигациям дается новая нечеткая формулировка теоремы ММ, лишенная недостатков традиционных детерминированной и стохастической постановок. В заключение рассматривается решение задач линейного лингвистического распознавания состояния экономических агентов при нечетком описании финансово-экономических параметров. Разрабатываются общие положения метода лингвистического распознавания и предлагаются новые взаимосвязанные подходы с использованием как двухмерных, так и многомерных моделей неопределенных параметров распознавания. Рассматриваются вопросы применения разработанного в третьем разделе инструментария оперирования с нечеткими числами для формирования линеаризованного представления шкалы качества лингвистического распознавания. аа

В заключении приводится перечень результатов диссертационного исследования, делаются выводы о возможности их практического использования и рассматриваются возможные направления дальнейшего развития этих исследований.

2. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ, ааВЫНОСИМЫЕ НА ЗАЩИТУ

1) Проведено теоретическое обоснование концепции макроэкономического моделирования процессов установления и поддержания общего экономического равновесия с широким учетом факторов субъективной неопределенности.

В настоящее время на базе критического рационализма происходит сближение двух основных направления экономической науки - теоретического и технологического исследования. С одной стороны, теоретические макроэкономические исследования пытаются распознать внутреннюю структуру, заложенную в многочисленных формах проявления экономической реальности, сформулировать по возможности простые и обобщенные гипотезы о причинно-следственных связях и закономерностях, проверить их эмпирически и воплотить в разъяснительных и прогнозных моделях. При этом научная ценность макроэкономического исследования не зависит от практической значимости объекта исследования: главное, чтобы оно проводилось методически чисто и логически правильно.

С другой стороны задачей технологических исследований в макроэкономике является содействие принятию решений менеджерами. Это означает, что макроэкономические модели принятия решений по целям и средствам должны разрабатываться как рекомендательная основа для действий по решению практических проблем фирм.

Обычно классические разъяснительные и прогнозные макроэкономические модели строятся таким образом, чтобы можно было использовать оптимизационный алгоритм и получить оптимальную практическую рекомендацию. Их недостаток заключается в вынужденном упрощении действительности, поскольку определение параметров модели связано с агрегированием и должно быть ориентировано на обеспечение самой возможности выработки решения. Отсюда рекомендации макроэкономического исследования могут потерять практическую ценность. Тем не менее, можно отметить и положительные стороны таких моделей: они не допускают логических ошибок, так как могут быть математически проверены на наличие нарушений логики. Кроме того, они являются бескомпромиссными и не содержат ничего лишнего: сводят экономическую проблему к ее сути и содействуют выражению основополагающих взаимосвязей целей и средств.

Близкие к практике рекомендации могут быть получены, если при построении модели принятия решений изначально отказаться от применения оптимизационных алгоритмов и придать большее значение учету существенных частных элементов наблюдаемого фрагмента экономической реальности. В результате будет формироваться противоположная оптимизационной имитационная модель. Такая модель уже не может быть представлена аналитически, а рассчитывается численно с применением компьютерных технологий. Однако такие модели часто опираются на интуитивные и умозрительные заключения конкретных менеджеров и могут не отражать перспективу развития экономической реальности. Поэтому для того, чтобы учесть возможности изменения действительности, часто в качестве базы имитационных моделей выступают оптимизационные модели.

Таким образом, практическая ценность оптимизационных макроэкономических моделей из-за вынужденного упрощения становится сомнительной. В то же самое время имитационные модели выполняют роль инструмента для решения сложных практических проблем, но не могут служить основой для решения задач макроэкономического характера. Это позволяет сформулировать проблему разработки путей сближения микро- и макроэкономических моделей. Такое сближение позволит, с одной стороны, учесть многообразие и скорость изменения экономической действительности в макроэкономических теоретических исследованиях. С другой стороны, за счет взаимного привлечения аппарата микро- и макроэкономического моделирования может быть расширена аксиоматика и обеспечена полнота этих экономических моделей. В качестве метода решения поставленной проблемы в данной диссертационной работе предлагается усовершенствование аппарата математических моделей макроэкономики, позволяющее приблизить результаты этих моделей к нуждам практики.

В различных областях науки математика и в особенности ее современная кибернетическая отрасль является бесспорным рабочим и связующим инструментом. Дальнейшее развитие многих дисциплин без внедрения системно-кибернетических методов просто невозможно. Вместе с тем в среде экономистов-практиков принято ставить этот факт под сомнение, поскольку такая оценка роли математических методов в экономике игнорирует тот факт, что даже самый лучший менеджер мыслит абстрактными моделями, поскольку постоянно может держать в поле зрения лишь немногие и сильно агрегированные взаимосвязи окружающей его реальности. В настоящее время учет экспертных мнений в экономических моделях осуществляется на основе традиционнойа теорииа вероятности, однакоа сама теория вероятности основана на системе аксиом, которые зачастую неадекватны решаемой задаче. Для этой теории характерна частотная интерпретация вероятности события, основанная на знании доли того или иного исхода во множестве всех возможных исходов эксперимента, многократно поставленного при неизменных начальных условиях. Если же внешние условияа постоянно изменяются, а эксперимент проводится однократно, то данный подход сталкивается с существенными затруднениями. Поэтому экспертныеа оценки вероятности того или иного события, вообще говоря, некорректны. Другая проблема состоит в том, что в теории вероятности предполагается, что случайные величины распределены по некоторому "хорошему" распределению (обычно распределению Гаусса). В этом случае расчеты существенно упрощаются. Такое предположение не лишено оснований при моделировании физических процессов (существует теорема оа том,а чтоа среднееа ота независимых случайных величин, распределенных по произвольным законам, распределено по Гауссу), но совершенно необоснованно в макроэкономике. Более того,а даже на финансовых рынках, где играет множество игроков, и заключается огромное число сделок, случайные величины не всегда подчиняются распределению Гаусса. Поэтому экспертные оценки среднего значения и стандартного отклонения случайной величины некорректны по крайней мере по трем причинам: во-первых, делается совершенно необоснованное и в большинстве случаев совершенно неверное предположение о характере распределения случайной величины, во-вторых, эксперт оказывается в ситуации, когда ему необходимо оценить трудно понятные с человеческой точки зрения параметры, в-третьих, иная информация, которой может обладать эксперт по крайней мере на подсознательном уровне (например, об истинном характере распределения) полностью игнорируется.

Предлагается новый подход к усовершенствованию математических макроэкономических моделей с использованием молодого и бурно развивающегося направления математики - нечеткой математики. Такой подход свободен от большинства недостаткова традиционных методов, изложенных выше.

В отличие от обычных понятий в рамках классической теории множеств, принципиальныма свойством понятия нечеткого множества является существование размытой границы между различными градациями того или иногоа качества экономического явления. Для описания этих качеств в нечеткой математике используются нечеткие множества, уровневые функции (характеристические функции или функции принадлежности) которых могут принимать значения из интервала [0, 1]. Такойа подхода позволяет полнее учитывать лингвистическую природу концепции субъективной вероятности, более корректно и эффективно использовать метод экспертных оценок, чем традиционная теория вероятностей. Однако применение такого подхода на практике привело к несовместимости решаемых таким образом задач с методами теории вероятности. С одной стороны, задачи теории нечетких множеств имеют характерную лингвистическую окраску и не связаны с процессами, имеющими вероятностный характер. С другой стороны, вводимые в теории нечетких множеств количественные оценки (уровни четкости, степени принадлежности, характеристические значения) не имеют ничего общего с оценками теории меры и, в частности, с вероятностной мерой.

Таким образом, математической проблемой в рассмотренной ситуации является поиск путей совместного использования методов теории систем и теории нечетких множеств для получения адекватных реальной экономической действительности математических моделей в макроэкономике.

В диссертационной работе предлагается разрешать указанные противоречия экономическо-математической теории за счет обобщения и совершенствования научно-методического аппарата исследования моделей и математических методов анализа микроэкономических процессов, методов моделирования мотивации фирм, домашних хозяйств и механизмов формирования спроса и предложения.

В качестве основного методологического положения решения проблемы предлагается использование концепции неаддитивной нечеткой меры. На базе этой концепции можно:

• получать новые результаты в областях, связанных с концепцией субъективной вероятности, в которых важно согласовать процедуры обработки информации с особенностями человеческого мышления, результирующие оценки которого не подчиняются аксиоме аддитивности;
• применить теорию нечеткой меры к задачам обработки информации о рыночной статике и динамике, представленной в виде нечеткого множества, отношения, отображения и развить на этой основе методы нечеткого макроэкономического анализа;
• обосновать решения по анализу, прогнозированию и управлению национальной экономической системой, реализация которых обеспечит долгосрочное поддержание равновесия рыночной экономики в современных геополитических и экономических условиях.

2) Проведено теоретическое обоснование применения нечетко-возможностного подхода к моделированию двойственности экономических явлений для решения проблемы повышения адекватности моделей общего экономического равновесия.

В большинстве макроэкономических задач приходится иметь дело с ситуациями, в которых следует учитывать множество онтологических аспектов и при этом обязательно принимать во внимание гносеологию сложных целостных экономических систем (ЦЭС).

Существует объективная двойственность в использовании математических структур при макроэкономическом моделировании ЦЭС: с одной стороны, как моделей для множества истинных формул, с другой стороны, как содержательно интерпретируемой модели реальной ЦЭС (рисунок 1).

 

Рисунок 1 - Математическая интерпретация двойственности

макроэкономических моделей

Основным инструментом теоретического разрешения данной двойственности выступает требование адекватности модели и реальной ЦЭС, а формализованными методами обеспечивающими адекватность модели и ЦЭС являются методы декомпозиции и агрегирования.

Существует два противоположных направления (школы) обеспечения требования адекватности макроэкономических моделей и ЦЭС: классическое и кейнсианское.

В классическом направлении (рисунок 2) возможность получения неформально-формальной декомпозиции и агрегирования макроэкономической модели может быть обоснована с использованием принципа единства учетной политики, который выполняется всеми структурными элементами в макроэкономической модели постоянно (принципы Вальраса и Сэя). При этом однако возникает не вполне адекватный реальным процессам эффект "нейтральности" денег и эффект неправильной дихотомии.

 

Рисунок 2 - Классическая двойственная схема макроэкономических взаимосвязей

Центральным моментом кейнсианского направления является введение в модели мотивационных механизмов ЦЭС классического принципа рыночного обмена "товар-деньги-товар" ("деньги-товар-деньги"). Однако при этом требуется выполнение перехода к рассмотрению неравновесного состояния экономики, не вполне адекватного реальным процессам.

В действительности невозможность полного выполнения условий адекватности концептуальных моделей и математически записанных эмпирических зависимостей зачастую приводит к ослаблению требований к истинности получаемых математических макромоделей. аМножество известных и описанных в настоящее время макроэкономических эффектов требуют более детального описания с помощью методов, составляющих формальный подход к макроэкономическому моделированию. Для этого следует формализовать основные макроэкономические концепции (концептуальные модели макроэкономических элементов), входящие в общий контур реакции производителей и потребителей на изменение цен.

Основу всех современных макроэкономических концепций составляют некоторые важные микроэкономические концепции, на основе которых и формируются макроэкономические концепции низшего уровня - концепции мотивации экономических агентов БФ и ДХ.

Во-первых, все ЦЭС ДХ сообразуют управление потреблением товаров и услуг как с собственным, так и с общим понятием об экономической полезности потребления, состоящей из двух аддитивных частей:

,

где а - полезность, соответствующая вектору потребительных свойств товаров ав количестве , определяет технологические или социально-психологические предпочтения;

а - полезность, соответствующая вектору стоимостных характеристик товаров , определяет предпочтения, основанные на мере стоимости;

авесовые коэффициенты.

При использовании данной функции полезности формулируется утверждение ("золотое правило потребления"): товары, для которых потребительная ценность оказывается меньше их цены, полностью исключаются из оптимального набора (набора количеств товаров, на котором достигается экономическое безразличие). Математическим выражением концепции мотивации потребления служит система уравнений Слуцкого:

аа аас функцией потребительной ценности:

. (1)

Во-вторых, концепция мотивации ЦЭС БФ основана на возможности отражения в понятии экономической эффективности производства (предложения) товаров присущей всем ЦЭС рациональной цели получения прибыли от экономической активности и формирование физического объема производства исходя из технологической (социальной) полезности потребления ресурсов (или факторов производства). Формально требуется найти компоненты вектора , обеспечивающие

апри,

где аэлемент матрицы удельных затрат ресурсов.

В результате решения этой задачи формулируется утверждение ("золотое правило производства"): при формировании физического объема производства ЦЭС исходя из технологической (социальной) полезности потребления ресурсов (или факторов производства) в производство включаются только те виды товаров, для производства которых характерно . То есть удельные производительности ресурсов в любом режиме (нормальном аи предельном ) обеспечивают не более единичного выпуска для данной технологической его ресурсоемкости. При этом формализованным выражением концепции мотивации производства служит система уравнений по математической конструкции аналогичных уравнениям Слуцкого:

аа

где аа 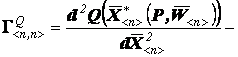агессиан функции предложения Q ЦЭС;

цены товаров и ресурсов соответственно.

Здесь по аналогии с (1) вводится функция возможности производства:

.а а (2)

Данный вывод подтверждает двойственность экономических явлений в отношении спроса и предложения в макроэкономических моделях.

Теперь для описания процессов установления и поддержания общего экономического равновесия (ОЭР) с учетом двойственности мотивации ДХ и БФ может быть использована концепция рационирования мотивации ЦЭС:

.аа (3)

Следует отметить, что выражение (3) для суперагрегированных моделей ОЭР представляют собой противоречивое уравнение связи нескольких параметров спроса в полезностном его аспекте и предложения в возможностном аспекте. При этом существуют и частные противоречия. С одной стороны, классическая теория явно исходит из микрооснов, однако не может объяснить некоторые важные макроэкономические явления, положенные в основу кейнсианского направления. С другой стороны, основные постулаты кейнсианского направления опираются лишь на эмпирические данные и не поддаются формализованному микроэкономическому описанию. При ближайшем рассмотрении макроэкономических рынков во всех его элементах: объектах рынка (товары и деньги), субъектах рынка (продавцы и покупатели), операциях субъектов рынка (продажи и покупки), механизмах рынка (предложение товаров и спрос на них), мотивации субъектов рынка и проч. проявляется двойственная природа экономических явлений. Поэтому можно предположить, что соединение нового (нечетко-возможностного) понимания двойственности экономических явлений с неоклассическим или неокейнсианским пониманием рыночных механизмов мотивации и определением роли рыночных агрегатов в процессе формирования стоимости товаров и полезности факторов позволит скорректировать обе теории и таким образом разрешить указанные противоречия.

3) Разработан новый методический аппарат макроэкономического моделирования с широким учетом целенаправленности моделей экономических агентов.

Математическая модель макроэкономической конъюнктуры (рыночных взаимосвязей макроэкономических субъектов) является математической структурой, заданной в виде совокупности отношений. Методы формальной декомпозиции макроэкономических моделей представляют собой в первую очередь методы декомпозиции отношений. Детерминированное теоретико-множественное описание макроэкономических взаимосвязей может быть получено с помощью методики проекционной декомпозиции отношения конечных счетных множеств бизнес-фирм (БФ), домашних хозяйств (ДХ) и слабо агрегированных рынков продуктов и услуг (РПУ) и факторов производства (РФП). Схема этих взаимосвязей представлена на рисунке 3. а

Микроэкономические взаимосвязи отдельных ДХ, БФ и рынков задаются восемью различными сечениями отношений предложения и спроса, связанными попарно и однозначно. Можно показать, что задание базовых условий, которым должны подчиняться сечения, полностью определит вид исходных бинарных отношений. В современных исследованиях рассматриваемого направления используются формулировки четырех базовых условий (известных как условия Бенасси-Бланчарда), отражающих жесткость разделения труда, жесткость структуры производства, равномерность структуры спроса на блага и равномерность структуры спроса на труд.

 

Рисунок 3 - Упрощенная схема взаимодействия рыночных агентов

Однако используемые в известных макроэкономических исследованиях модификации данных условий направлены в основном на сужение общего поля взаимосвязей, что приводит лишь к упрощенным моделям, удовлетворяющим каноническим условиям совершенного рынка.

Предлагается при переходе к моделированию более глубоких количественных взаимодействий макроэкономических субъектов рассматривать их как ЦЭС с моделями внутренней структуры (рисунок 4).

 

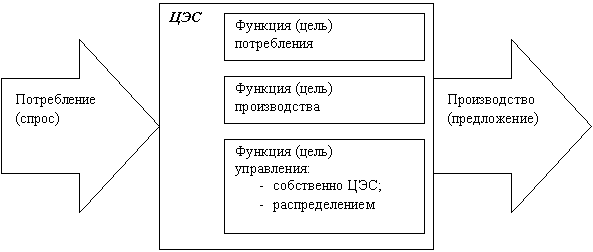
Рисунок 4 - Схема мотивационных моделей элементарной ЦЭС

Каждая из этих моделей отражает две главные сферы экономической активности: производство и потребление товаров и услуг и формирует входную (функцию спроса) и выходную (функцию предложения) передаточные функции ЦЭС. При этом переход от модели отношений супер-ЦЭС (производство-потребление) к количественным характеристикам отдельных ЦЭС связан с введением математического отображения и его горизонтальной декомпозиции. Основные свойства элементарной ЦЭС в макроэкономической модели можно записать в виде двух математических отображений: отображения (функция) спроса и предложения , заданных на множествах валового потребления элементарной ЦЭС (спрос) и валовых продуктов/услуг элементарной ЦЭС (производство/предложение). Пара отображений аопределяет условия и способы вовлечения фактор-множеств (элементов труда, земли, капитала, предпринимательской деятельности и стратегий управления ЦЭС) в экономическую активность и с практической точки зрения представляет собой передаточную функцию ЦЭС.

На моделях с передаточными функциями ЦЭС можно определить понятие общего экономического равновесия как состояния экономики, при котором на всех рынках одновременно достигнуто равновесие между спросом и предложением и ни одна из ЦЭС в рыночных сделках не имеет экономической мотивации к изменению объемов производства и пропорций обмена (покупок или продаж).

Применение правил горизонтальной декомпозиции передаточных функций ЦЭС (как математических отображений) позволяет определить необходимые и достаточные условия общего экономического равновесия, которые соответствуют известному закону Вальраса в широком смысле.

ТЕОРЕМА 1. Пусть выполнены условия горизонтальной декомпозиции

(4)

И сформулированы четыре основные задачи ЦЭС БФ и ДХ:

а аа (5)

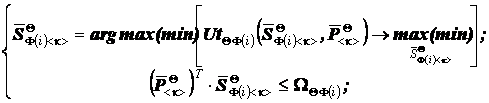а аа (6)

аа (7)

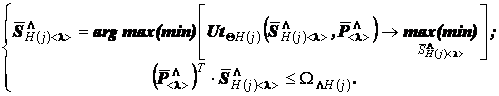(8)

Кроме того, выполнены следующие условия:

• все множества поиска экстремума в (5)-(8) замкнуты, выпуклы и имеют нижнюю границу;
• все целевые функции (обозначение Ut) в (5)-(8) дважды непрерывно дифференцируемы и вогнуты (при максимизации) или выпуклы (при минимизации) по всем аргументам;
• выполнены по крайней мере условия Бенасси-Бланчарда.а

аа Тогда для обеспечения ОЭР в декомпозиционной модели (4)-(8) в виде

(9)

необходимо и достаточно существование набора нечетких чисел

,

для которых выполняется:

а ааа

В диссертационной работе показано, что для рассматриваемых моделей ЦЭС существование общего экономического равновесия (ОЭР) связано с двойственностью взаимовлияния ДХ и БФ. При этом в результате анализа схемы экономической активности при установлении ОЭР выявлены следующие особенности макромоделей, полученных из решения (4)-(9):

• основное различие направлений макроэкономического моделирования заключается в методах аучета неопределенности при рассмотрении арезультирующего равенства валового национального дохода Y и суммы многопродуктового и инвестиционного спроса;аа
• синтез моделей ОЭР заключается в поиске по крайней мере двух передаточных функций обратной связи, характеризующих мотивацию ЦЭС, в результате которых модель экономики приобретает свойство замкнутости и, следовательно, саморегулируемости;
• производственная функция (ПФ) является единственной общей для любой макроэкономической концепции передаточной функцией обратной связи БФ. При этом в зависимости от требований к макромодели ПФ могут выбираться аиз атрех аклассов: астатические, аадаптивные аи арациональные. аВ условиях значительного влияния инфляции необходимо учитывать в ПФ в качестве факторов субъективной неопределенности мотивации БФ оценку будущей величины реальной и номинальной прибыли;
• традиционное определение в макромоделях инвестиционного предложения со стороны ДХ некорректно и должно быть заменено предложением инвестиций (инвестиционных проектов) со стороны БФ и спросом на "квазиденьги" в виде инвестиций со стороны ДХ. При этом в классических моделях следует рассматривать дополнительный рынок инвестиций - ФР(I), на котором в качестве цены выступает текущая скидка 1 - R на будущую стоимость инвестиций.

4) Разработан новый класс макроэкономических моделей - нечетко-возможностные модели на основе математических конструкций пространства с нечеткой мерой.

аа В результате анализа классической схемы введения неопределенности в макроэкономические модели финансового рынка выявлено следующее:

• полученные вероятностные математические модели легко трансформируются в классические детерминированные условия ОЭР в случае нулевых ковариаций между будущей стоимостью инвестицонных ценных бумаг (ИЦБ) и прогнозом будущего инвестиционного предложения. Для всего рынка условие ОЭР выводится в виде равенства сбережений (спрос) и предложения инвестиций со скидкой .
• в полученной математической модели явно выделяются составляющие безрисковой части спроса на ИЦБ и добавка за риск, связанный с ожидаемой полезностью стремления стоимости ИЦБ к будущей величине.

а(10)

где , - текущие и предполагаемые рыночные котировки всех рисковых бумаг;

- прогноз будущего инвестиционного предложения;

- мера склонности j-го ДХ к риску;

- детерминированная эффективность портфеля.

При этом в действительности рисковая добавка является суперпозицией показателя распределения случайной величины вариации стоимости ИЦБ и показателя субъективной полезности, связанной с обобщенной по всему рынку мерой склонности ДХ к риску спроса. Из последнего следует, что при анализе конкретной рыночной ситуации возможны два случая: преобладание в мотивации ДХ объективно непредсказуемой случайной составляющей, либо преобладание субъективной целенаправленной составляющей. От реализации того или иного случая существенно зависит и выбор математических методов и инструментов моделирования - классической теории вероятностей или теории возможностей Л. Заде (или их комбинации).

Однако согласно общим представлениям системного подхода неопределенность, как основной сопутствующий фактор при разрешении вопроса сложности, оказывается также сложно структурированным понятием и одним из важнейших инструментов обеспечения адекватности выводов исследований реально происходящим в экономике процессам. Вследствие многозначности факторов неопределенности операции с числовыми оценками неопределенности, если таковые можно представить в рамках теоретико-множественного подхода, имеют смысл только в том случае, когда эти оценки отражают один, и только один фактор (либо общую группу факторов) неопределенности для всех участвующих в операции операндов. Для учета этой особенности в экономической предметной области предложена новая трактовка парадигмы неопределенности (рисунок 5).

 

Рисунок 5 - Многомерная парадигма неопределенности

В такой трактовке детерминированность в необходимом смысле парадигм Канта и Л. Заде формируется двумя факторами: собственно фактором необходимости (правдоподобность) и аксиологическим фактором (нечетко-полезностный). При этом учитывается, что аксиологический фактор связан с нечеткой оценкой альтернатив, а поссибилический - с нечеткой оценкой структуры предмета. Переходы от возможности к действительности рассматриваются через лингвистическую неопределенность по любому из двух путей. При переходе собственно через неопределенность лингвистический аспект может включать как частный случай не только поссибилическую, но и вероятностную неопределенность. При переходе через детерминированность лингвистический аспект как частный случай включает правдоподобность (необходимость в смысле Канта) и аксиологическую (нечетко-полезностную) неопределенность.

Для формализации новой парадигмы неопределенности предлагается определение лингвистического возможностно-полезностного пространства, в котором исследуется преобразование возможности в действительность. Математическое описание этого пространства представляется в виде тройки , включающей лингвистическое множество произвольных символов (поле языковых, машинных, кодовых и проч. понятий ), семейство аподмножеств множества , замкнутое относительно заданных правил выполнения теоретико-множественных операций объединения, включения и пересечения, а также универсальное отображение , определенное на лингвистическом множестве . Предложена новая трактовка понятия нечеткого множества как элемента лингвистического возможностно-полезностного пространства или как нечеткой лингвистической структуры прикладной задачи. Для этого, по аналогии с подходом Колмогорова, строго определены основные аксиомы лингвистического нечеткого исчисления.

В качестве основного примера применения нечетких лингвистических структур в моделях макроэкономики в диссертации разработана концепция решения задач нечеткой оптимизации. Показано, что без потери общности можно рассматривать всего два основных подхода к решению задач нечеткой оптимизации (ЗНО): подход на основе трансформации ЗНО к задаче "четкой" оптимизации (приближенный подход в виде A-постановки или робастной постановки и интегральный подхода на основе I-постановки), а также прямой подход без перехода к задаче "четкой" оптимизации - подход на основе интегральной возможности (P-постановка) и подход на основе ожидаемой полезности (MU-постановка). Разработаны основные положения интегрального похода (I-постановка), основанного на возможности "свертывания" любого нечеткого числа с помощью интегрирования по Лебегу его уровневой функции на базовом множестве и получения двух типов функций с нечеткими аргументами и "четкими" значениями.

После трансформации ЗНО с использованием индикаторных функций LE и GE ЗНО можно представить в следующем "четком" виде:

а либо ,

при условиях ; или а,

где аа ? - заданное концепцией возможности (полезности) значение показателя предельного (приемлемого) ухудшения эффектов.

5) Разработан математический аппарат нечеткой алгебры для повышения адекватности моделирования процессов в сложных экономических системах с использованием нового понятия предикатных смесей.

В последнее время для математического описания нечетких чисел все шире используется понятие и соответствующий аппарат нечеткого предиката возможностей. Для выполнения практических расчетов с нечеткими числами необходимо задать две элементарные алгебры: алгебру арифметических бинарных операций ("сложение", "вычитание", умножение" и "деление") и алгебру логических бинарных операций ("больше", "меньше", "равно" и их производные). Предлагается в качестве основы алгебры арифметических операций с нечеткими числами применять принцип обобщения, согласно которому результатом любой нечеткой операции должно быть нечеткое число, определенное в той же форме.

Одним из конструктивных направлений практической реализации алгебры операций с нечеткими числами является задание предикатных смесей, которые удовлетворяют введенному принципу обобщения. Для его реализации введено понятие и математическое описание аппарата предикатных смесей с использованием транзитивного высказывания, истинность которого определяется специальной трижды вложенной математической функцией:

Mix@ = ,а (11)

где аа L@а - отображение ав общем случае многозначное в силу многозначности выражения апри различных операндах x и y и постоянном результате z.

M@ - однозначная функция многих переменных , обеспечивающая инъективность предиката апутем свертки множества значений L@ в единый показатель.

На примерах нескольких наиболее распространенных функций транзитивной смеси типа функций "пессимистического оптимиста" или мини-максных смесей можно показать, что "свертка" цепочки высказываний макроэкономического субъекта, выполняемая с целью адаптивно-рационального определения единого показателя выбора, может осуществляется аналогично выполнению нечетких арифметических операций на основе предикатных смесей (11).

Алгебра арифметических операций с нечеткими числами может служить математической моделью расчета показателя выбора в процессе принятия субъективного решения ДХ или БФ. При этом введение предикатной смеси в виде некоторой математической функции открывает широкие возможности к статистическому подтверждению адекватности введенной алгебры операций с нечеткими числами и реальному мыслительному процессу выбора конкретного макроэкономического субъекта. Однако применение менее точного и "надежного" субъективного выбора на практике оправдано лишь тогда, когда более точный и "надежный" объективный выбор по каким-либо причинам невозможен.

Основным отличием определенного на предикатных смесях математического аппарата алгебраических операций с нечеткими числами является наличие трех противоречий:

• неэквивалентность замены многократного умножения и деления нечетких чисел аналогами операций возведения в степень четких чисел, что требует в общем случае выполнения численно-аналитических алгоритмов;
• невозможность однозначного определения выражений аи для любых значений x;
• невозможность указать единое и однозначное выражение для нечетких чисел "ноль" и "единица". В общем случае можно лишь указать включение соответствующего четкого значения 0 или 1 в базовое множество аили а(здесь дополнительные трудности могут возникнуть при одновременном включении 0 и 1).

аа Данные противоречия приводят к невозможности в нечетком виде определить математическое понятие "уравнение". Поэтому в качестве конструктивного подхода предложено три направления разрешения указанных противоречий:

• оставить без изменения введенные определения, полагая, что числа "ноль" и "единица" формируются нечетким методом по контексту соответствующих арифметических операций;
• ввести исключения для операций деления и вычитания: аи 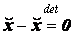. Данные исключения обеспечивают теоретическую возможность эквивалентных преобразований в алгебраических выражениях с нечеткими операндами. Однако это может привести к потере адекватности математической модели;
• перейти к лингвистическому определению нечетких чисел. При этом каждому конкретному числу присваивается уникальное наименование, связанное с качественным описанием экономических процессов или какой-либо качественной шкалой лингвистически определенных значений.

Для выполнения нечетких логических операций с нечеткими числами на предикатных смесях предложено использовать метод определения нечеткого логического числа на основе задания логического базового множества. Учитывая указанное выше свойство неэквивалентности переноса нечетких чисел в противоположные части неравенств, предложено заменять исходную задачуа азадачей поиска некоторого значения , допускающего диапазонное представление и в каком-то смысле характеризующего интервальное неравенство. На этой основе разработан обобщенный подход к реализации функции ас использованием теоретико-множественного понятия о соотношении мощности множеств. В результате определено понятие нечеткого логического числа в виде нечеткого множества . В качестве его практической реализации на основе вычисления характеристики амощности зависящего от неравенства множества апредложено -уровневое решающее правило выполнения нечеткого неравенства.

. (12)

Показано, что для этого правила нечеткое множество , объединяющее все пары значений аи определенное на базовом множестве-носителе , можно считать нечетким показателем выполнения нечеткого неравенства. Для упрощения практических расчетов предложен четкий индикатор выполнения нечеткого неравенства.

Для рассмотрения практических вопросов применения предложенного математического инструментария выполнена компьютерная реализация разработанных алгоритмов в виде программного комплекса "Нечеткий процессор". Результаты тестирования нечетких бинарных алгебраических операций с числами, заданными на базовых множествах элементарными линейными уровневыми функциями аргументов, показали справедливость только некоторых свойств, характерных алгебраических операций. Так, для сложения и вычитания выполняются свойства: коммутативность, обратимость и ассоциативность совместно с операциями умножения и деления; для операции умножения - возможность замены операций умножения на деление на обратное число; для операции деления нечетких чисел показана невозможность содержания числа "нуль" в базовом множестве делителя. Показано, что уровневая функция результата операции деления почти всегда содержит нелинейные участки с обратными функциями, несмотря на то, что ее аргументы имеют только линейные уровневые функции. Таким образом, после выполнения любой из операций умножения или деления в дальнейшем к результату операции возможно применение только приближенной кусочно-линейной методики.

6) Разработана нечетко-возможностная линейная магистральная модель рыночной экономики в матричной форме.

аа В рамках магистральной теории в работе подробно рассмотрен класс динамических моделей в матричной форме. Сформулированы основные допущения модели , представляющие собой утверждения, в которых дается (полное для математических целей) формальное описание соотношений между используемыми понятиями. На основании принятых допущений получены две группы векторно-матричных линейных неравенств: , описывающая производственную (технологическую) сферу модели ; , описывающая ценностную сферу модели . Модель апредставляет собой объединение своих частей: , что полностью соответствует рассматриваемой в работе проблеме учета двойственности в экономико-математических моделях.

Для модели , с учетом предложенных условий и постановок задач поиска стационарной траектории максимального экономического роста, сформулирована и доказана обобщенная теорема магистрального подхода вне зависимости от характера учета неопределенности.

ТЕОРЕМА 2 (о магистрали в M-постановке). Пусть рассматривается задача оптимизации вида:

; аа (13)

где аа а - заданный вектор приоритетов (весов, значимости и проч.) конечной интенсивности процессов;

азаданный начальный вектор интенсивностей процессов.

Если квадратные матрицы затрат аи выпуска аопределяются либо моделью , либо моделью анезависимых нормально распределенных величин, либо моделью анечетких чисел с симметричными уровневыми функциями и не зависят от номера t, то имеют место следующие утверждения:а

1) найдется номер , такой, что при любом номере t из диапазона атраектория решения задачи (13) с любой из перечисленных трех моделей (оптимальная траектория ) удовлетворяет равенству:

,

где функция M[*] для модели аозначает собственно элементы матрицы; для модели а - математическое ожидание элементов; для модели а - точка максимального уровня неопределенности элементов;

2) для любого сколь угодно малого числа анайдется номер , такой, что при любом номере t из диапазона атраектория решения задачи удовлетворяет неравенству:

,

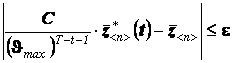где аа С - аскалярный множитель, зависящий от вектора а - решения задачи о магистрали , при выполнении условий октаэдрической нормировки начальных интенсивностей , аи условий надежности роста экономики:

- по неравенству для модели :

;а а (14)

- по вероятности для модели :

;а (15)

- по возможности для модели :

.аа (16)

Практические расчетные примеры подтвердили справедливость теоремы о магистрали в сформулированных условиях. Сравнение результатов решения задачи поиска нечеткой траектории экономического роста (рисунок 6) с оптимальным конечным состоянием с решениями в D-постановке и стохастической M-постановке показало очевидное их сходство.

7) Разработана нечетко-возможностная агрегированная динамическая модель многосекторной экономики.а

Предложена новая обобщенная нечетко-возможностная динамическая модель, учитывающая целевой характер матриц затрат и выпуска в магистральной модели, что определяет главный смысл экономической стороны общества в целом. В простейшем случае для этого предложено использовать идею Вальраса, связанную с двумя допущениями.

Рисунок 6 - Примеры решения задачи оптимального стационарного

экономического роста в нечеткой M-постановке

Во-первых предполагается, что для всех продуктов, БФ и ДХ определены строгие лингвистические границы. При этом продукты, БФ и ДХ связаны между собой рассмотренными в первом разделе работы отношениями конкуренции. Таким образом БФ и ДХ являются однородными потребителями.

Во-вторых, предполагается, что матрицы производственных возможностей и потребительской способности экономики обеспечивают общее условие достаточности производства для конечного потребления (допущение об открытой экономике). С использованием этих допущений на основе дополнительного определения задач целеполагания БФ и ДХ объединенная задача о магистрали с терминальными целями развития экономики, формулируется как многокритериальная задача оптимизации.

Показано, что без существенной потери общности динамическая межотраслевая модель (модель В. Леонтьева) определяется неравенством вектора будущих затрат продуктов и вектора текущего валового выпуска продуктов: .

Для фактического определения динамики межотраслевого обмена необходимо: провести факторный анализ затрат, в которых выделяется три основные части - потребление, инвестиции и накопление (добавленная стоимость); в первом приближении потребление представить как межотраслевой обмен прямыми затратами; в первом приближении инвестирование представить как мгновенный (за один период) процесс превращения текущего выпуска в планируемые на будущее капитальные затраты.

Если накопление добавленной стоимости в модели Леонтьева возможно представить двумя эквивалентными способами (способом "внутреннего" конечного потребления ДХ или способом экспортно-импортного сальдо), то в результате простого обозначения эта модель оказывается полным математическим аналогом модели Неймана (13)-(16) с измененными нечеткими условиями надежности роста экономики (блочно-матричный математический аналог модели Неймана):

- с использованием четких интегральных индикаторов неравенства

(17)

- с использованием нечетких интегральных индикаторов неравенства

(18)

- с использованием нечеткой ожидаемой полезности (нечеткого интеграла по нечеткой мере):

аа (19)

где а - нечеткая мера полезности нулевого значения разности величин, сравниваемых в нечетком предикате возможностей.

Следовательно, основная теорема магистрального подхода (теорема 2) в соответствующем смысле может быть применена и к модели В. Леонтьева.

Для получения макроэкономических моделей краткосрочного периода предложено использовать агрегированную модель односекторной экономики с распределенным лагом: полученный БФ со стороны ДХ в момент аденежный спрос IM далее осваивается, постепенно переходя в поток капиталовложений IK в соответствии с заложенной в БФ функцией стратегии развития БФ. В качестве элементарной стратегии предлагается стационарное распределение (элементарное бизнес планирование развития) при условии неизбежного освоения инвестиций. При этом динамика переходных процессов в агрегированной модели без учета банковской системы полностью определяется соотношением двух параметров запаздывания - темпа освоения (преобразования в фактор-капитал) инвестиций (параметр субъективной полезности) и сложным процентом, определяющим доходность инвестиций (параметр рациональной возможности). В простейшем случае два параметра могут быть заменены их соотношением, которое формально можно считать макроэкономической ценой (1 - R) капиталовложений на инвестиционном рынке ФР(I). Детерминированная модель односекторной экономики в относительных макроэкономических показателях обладает свойством устойчивости по Ляпунову для любой неоклассической макроэкономической производственной функции. Стохастический и нечеткий вид модели односекторной экономики зависит от принятия соответствующих законов распределения и уровневых функций для параметров запаздывания.

8) Разработана нечетко-возможностная модель функционирования фондового рынка, на основе которой предложено новое доказательство теоремы Миллера-Модильяни.

Известная классическая методикаа выбора структуры акционерного капитала на основе решения задач оценивания стоимости БФ сводится к доказательству инвариантности стоимости БФ по отношению к структуре ее капитала (теоремаа ММ), имеет не только сильные, но и слабые стороны. Предложена коррекция этого доказательства и формулировка теоремы ММ, основанная на введении допусков и применении методов нечеткой алгебры. Необходимость в некоторой корректировке классического доказательства (отмеченная еще самими авторами ММ) объясняется тем, что выполнить одно из основных допущений теоремы ММ на реальном рынке капитала оказывается невозможно. В результате доказательство, построенное, в частности, на том основании, что инвесторы (как ДХ) могут получать кредиты под те же проценты, что и юридические лица - БФ, или что ставки по облигациям сравняются со ставками по кредитам, становится неочевидным и вполне может быть опровергнуто.

В результате более подробного анализа условий теоремы ММ показано, что в идеальных детерминированных условиях для обеспечения выравнивания стоимостей в арбитражном процессе БФ с долговой нагрузкой должна иметь коэффициент левереджа , представляющий собой некоторую взвешенную сумму отклонений коэффициентов рентабельности собственного капитала БФ (отношение ) от соответствующих ставок по долговым обязательствам. При этом коэффициенты вариации рыночных ставок интегрально (или мультипликативно) отражают индивидуальные кредитные способности акционеров и кредитоспособность БФ в целом.

В условиях несовершенного рынка усредненная на достаточно большом промежутке времени стоимость "левереджных" БФ данного класса K всегда больше усредненной на том же интервале стоимости БФ, не имеющих долгов. Таким образом в рыночной экономике реализуется возможность постоянного роста стоимости денег во времени при сохранении общей стабильности в развитии. При этом ожидаемый уровень доходности на акциюj-й "левереджной" БФ данного класса зависит от используемого ею кредитного рычага аи является нелинейной функцией интервального типа с несимметричными к относительной стоимости фирмы аграницами интервалов . Предложена методика расчета коэффициентов ав стохастической постановке. Показано, что в случае нечеткой формулировки теоремы ММ для данного класса БФ K существует (единственная) нечеткая величина коэффициента капитализации , при которой выполняется соотношение:

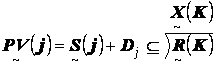адля всех ,

где справа от знака нечеткого подмножества аобозначено нечеткое отображение типа арифметической операции деления. Доказательство нечеткой теоремы ММ сводится к поиску нечеткой единицы, что на практике оказывается эквивалентно оценке выполнения нечеткого неравенства

.

9) Разработана методика нечетко-возможностного лингвистического распознавания экономического состояния рыночных агентов в макроэкономических моделях.

В сложившихся условиях слишком большого разнообразия числовых характеристик экономических аспектов деятельности БФ одним из наиболее результативных методов решения задачи определения некоторого качества БФ является двухэтапный метод лингвистического распознавания. В случае невозможности согласовать с выбранной целью конкретный состав и значения показателей для получения "конструктивной" классификации можно попытаться агрегировать некоторую совокупность этих показателей и их значений в ограниченное число лингвистически ясных качественных понятий путем опроса экспертов

Принимая во внимание тот факт, что эксперты (сознательно или подсознательно) в своих ответах уже оценили взаимосвязь параметров при определении их соответствия заданному качеству, задачу распознавания можно рассматривать на каком-либо априорном предположении о классе взаимосвязи параметров. В самом простом случае предполагается линейная взаимосвязь типа элементарного взвешивания. Это предположение может быть заложено в виде некоторого условия в опросные листы при получении экспертных мнений. Тогда предположение о классе взаимосвязи типа "взвешивание" может стать более обоснованным. В любом случае количественную связь параметров системы в заданном предположении можно записать в виде:

аа аа (20)

гдеа a1, a2, C - заранее неизвестные параметры взаимосвязи.

Учитывая, что (20) имеет в рассматриваемом контексте лишь условный смысл, обе части равенства (20) можно разделить на a2. Тогда в результате перегруппировки получим:

, ; .а (21)

Графически зависимость (21) можно изобразить в двух вариантах, представленных на рисунке 7.

 

Рисунок 7 - Особенности линейной взаимосвязи двух показателей качества

а Если положить C > 0, то коэффициенты в (21) можно определить по формулам:

в случае обратной зависимости а

в случае прямой зависимости

где

; ;

.

Тогда простейшая задача двухмерного распознавания качества экономической системы формулируется в виде:

а (22)

где аа ;

Смысл равенства (22) заключается в вычислении возможности присвоения экономической системе заданного значения лингвистического качества при условии, что функция [*] является уровневой функцией нечеткого числа , а показатели качества системы принимают известные значения x1, x2 и имеют устойчивую прямую или обратную взаимосвязь.

Для определения конкретного лингвистического значения качества системы достаточно построить некоторую лингвистическую шкалу аи для каждого лингвистического значения вычислить согласно (22) числовые значения возможностей , соответствующие конкретным значениям параметров x1 и x2.а Тогда максимальное значение в наборе абудет определять искомое качество системы.

На практике более "удобным" оказывается распознавание по единой для всех лингвистических градаций горизонтальной оси. Для этого в (22) можно использовать нечеткую величину , однозначно связанную с величиной . Тогда новая запись решения двухмерной задачи распознавания лингвистического качества экономической системы примет вид:

аа а аа (23)

гдеаа аа Смысл равенства (23) аналогичен (22). Однако теперь для решения задачи распознавания достаточно для каждого лингвистического значения из набора Q записать формулу нечеткого числа . Подставив в полученные формулы одно и то же значение показателя качества x2, можно вычислить соответствующие числовые значения возможностей . Максимальное значение в наборе абудет определять искомое качество системы.

Характерно, что полученное в (23) нечеткое число апо обозначению совпадает с числом, заданным исходными данными на рисунке 7. Однако при этом в (23) апредставляет собой одностороннее ?-число, как показано на рисунке 8.

Рисунок 8 - Односторонние решающие правила нечеткого распознавания

В отличие от рисунка 7 представленные на рисунке 8 графики можно назвать решающими правилами в задаче распознавания. Рассчитанные для всего набора значений лингвистической переменной Q решающие правила составляют относительную шкалу распознавания качества экономической системы на базе выбранного (опорного) показателя качества x2.аа

Трудности распознавания могут значительно возрасти при получении многомерных шкал по множеству показателей качества. Поэтому в диссертации также предложено несколько эффективных конструктивных методик получения (обучения) взаимосвязи нечетких показателей качества с линейными и кусочно-линейными уровневыми функциями.

Так, обобщая (22)-(23) на многомерный случай, вначале можно записать линейную связь параметров системы в виде:

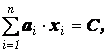а (24)

гдеа C, ai, i = 1,Е,n - заранее неизвестные параметры взаимосвязи.

Затем в результате перегруппировки получим:

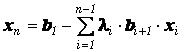,а а (25)

где а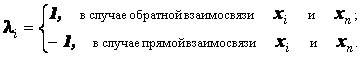а ; ;

а

При наличии исходных данных экспертного опроса в виде матрицы

алгоритм обучения распознавания для (25) примет следующий вид:

аЕ

аа (26)

где аа

Работоспособность предложенной методики (26) доказана теоретически и апробирована на примерах распознавания банкротства фирм в РФ за период с 2001 г. по 2009 г.

ОСНОВНЫЕ НАУЧНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИОННОГО ИССЛЕДОВАНИЯ

Монографии, брошюры, учебники и учебные пособия:

• Радионов Н.В. Модели эффективности инвестиций и кредитования. Часть 1. Основы финансового анализа: Монография. - СПб.: Наука, 2005. - 37,5 п.л.
• Радионов Н.В., Радионова С.П.а Оценка инвестиционных ресурсов предприятий: инновационный аспект: Монография. - СПб.: Изд-во Альфа, 2001. - 13 п.л.(авт. вклад - 3 п.л.).
• Радионов Н.В., Радионова С.П. Основы финансового анализа: математические методы, системный подход: Монография. - СПб.: Изд-во Альфа, 1999. - 37 п.л. (авт. вклад - 30 п.л.).

Статьи, опубликованные в ведущих рецензируемых научных журналах

и изданиях, рекомендованных ВАК России:

• Радионов Н.В., Антонов Г.А. Об одном подходе к анализу финансовых показателей ликвидности // Известия Санкт-Петербургского университета экономики и финансов. - 2004. - №3(39). - С. 67-77 - 0,8 п.л. (авт. вклад - 5 п.л.).
• Радионов Н.В. Письмо в редакцию // Аудит и финансовый анализ. - 2005. - №2. - С. 248-252. - 0,3 п.л.
• Радионов Н.В. О реальных опционах // Аудит и финансовый анализ, 2005. - №3. - С. 157-164. - 0,45 п.л.
• Радионов Н.В. Соколов Д.В. Об одной корректировке доказательства теоремы Миллера-Модильяни // Аудит и финансовый анализ. - 2006. - №1П. - С. 58-70. - 1 п.л. (авт. вклад - 0,5 п.л.).
• Радионов Н.В. Консультант на распутье // Аудит и финансовый анализ. - 2006. - №2П. - С. 122-127. - 0,4 п.л.
• Радионов Н.В. Тонкая грань: налоговая оптимизация или уклонение от налогов? // Аудит и финансовый анализ. - 2007. - №1. - С. 54-78. - 1 п.л.
• Радионов Н.В., Алябьева С.Г., Горбулин В.И., Макаров Ю.Н. аО задаче технико-экономического обоснованияа финансирования операций по развертыванию и наращиванию систем малых космических аппаратов // Успехи современной радиоэлектроники. - 2010. - №3. - С. 42-48. - 0,4 п.л. (авт. вклад - 0,1 п.л.).

Публикации в профессиональных журналах и научных сборниках:

• Радионов Н.В. Разработка и практическая реализация программ подготовки инвестиционных и финансовых менеджеров на продвинутом уровне // Сборник тезисов докладов 5-й ежегодной конференции по управлению, 1999. - С. 20-23. - 0,1 п.л.
• Радионов Н. В., Антонов Г.А. Нечетко-возможностный подход к анализу ликвидности // Регион: Политика, Экономика, Социология. - 2002. - а№5. - С.23-30. - 0,9 п.л. (авт. вклад - 0,5 п.л.).
• Радионов Н.В., Горбулин В.И., Панченко В.В. Выбор системы малых космических аппаратов и состава бортовой аппаратуры для комплексного наблюдения заданного района // Известия высших учебных заведений. Приборостроение. - 2009. - №1(52). - С. 26-32. - 0,45 п.л. (авт. вклад - 0,15 п.л.).
• Радионов Н.В., Соколов Д.В. Применение концепции нечеткой меры для решения экономических задач многокритериального оценивания и выбораа // Экономическая кибернетика: системный анализ в экономике и управлении: Сборник научных трудов. - 2010. - №21. - С. 45-53. - 0,4 п.л. (авт. вклад - 0,1 п.л.).
• Радионов Н.В., Соколов Д.В. Методика технико-экономического обоснования инвестиций в повышение безопасности функционирования промышленных предприятий // Экономическая кибернетика: системный анализ в экономике и управлении: Сборник научных трудов. - 2010. - №21. - С. 18- 27. - 0,5 п.л. (авт. вклад - 0,25 п.л.).
• Радионов Н.В., Антонов Г.А., Радионова С.П. Перспективы развития внешнеторговой деятельности в Санкт-Петербурге // Конкурентоспособность российской экономики (проблемы и перспективы): Сборник научных трудов. - СПб.: Изд-во СПбГУЭФ, 2003. - С. 59-65. - 0,4 п.л. (авт. вклад - 0,1 п.л.).

Доклады на научных конференциях и другие научные публикации:

• Радионов Н.В. Концепция нечеткой меры и ее применение для решения экономических задач многокритериального оценивания и выбора // VI Московская международная конференция по исследованию операций (ORM2010): Труды, 19-23 октября 2010 года. / Отв. Ред. П.С. Краснощеков, А.А. Васин. - М.: МАКС-Пресс,а 2010. - С. 192-194. - 0,1 п.л.
• Радионов Н.В., Радионова С.П. Методика технико-экономического обоснования инвестиций в повышение безопасности функционирования промышленных предприятий // VI Московская международная конференция по исследованию операций (ORM2010): Труды, 19-23 октября 2010 года. / Отв. ред. П.С. Краснощеков, А.А. Васин. - М.: МАКС-Пресс,а 2010. - С. 116-118. - 0,1 п.л. (авт. вклад - 0,05 п.л.).
• Радионова Н.В., Воробьев А.М., Долбенков В.Г., Макаров Ю.Н. аМетодика технико-экономического обоснования инвестиций в повышение безопасности функционирования стартовых комплексов ракет космического назначения // Актуальные проблемы защиты и безопасности: Труды ХIII Всероссийской научно-практической конференции РАРАН, 05-08 апреля 2010 года: Сборник докладов. - Т.1 - СПб.: Изд-во НПО Спецматериалы, 2010. - С. 438-454. - 1 п.л. (авт. вклад - 0,5 п.л.).
• аРадионова Н.В., Воробьев А.М., Долбенков В.Г., Макаров Ю.Н. Методические основы постановки задач технико-экономического проектирования // Актуальные проблемы защиты и безопасности: Труды ХIII Всероссийской научно-практической конференции РАРАН, 05-08 апреля 2010 года: Сборник докладов. - Т.1. - СПб.: Изд-во НПО Спецматериалы, 2010 - С. 455-471. - 1 п.л. (авт. вклад - 0,5 п.л.).
• Радионов Н.В., Соколов Д.В. Решение задач управления предприятием с применением инструментов нечеткой логики // Управление развитием отечественных компаний на основе инновационной активности: проблемы и перспективы: Материалы межвузовской научно-практической конференции 25 мая 2010 года / Под ред. Ю.П. Григорьева. - СПб.: Изд-во Политехн. ун-та, 2010. - С. 58-63. - 0,3 п.л. (авт. вклад - 0,15 п.л.).
• Радионов Н.В., Алябьева С.Г., Горбулин В.И., Макаров Ю.Н. аАнализ структурных свойств транспортных операций по развертыванию, наращиванию или восполнению орбитальных систем КАа // Рук. деп. в ЦВНИ МО РФ, 2010. - 0,45 п.л. (авт. вклад - 0,15 п.л.).
• Радионов Н.В., Алябьева С.Г., Горбулин В.И., Макаров Ю.Н. Методика технико-экономического обоснования инвестиций в повышение безопасности функционирования стартовых комплексов космодромов // Рук. деп. в ЦВНИ МО РФ, 2010. - 0,9 п.л. (авт. вклад - 0,6 п.л.).
• Радионов Н.В., Макагонов А.В., Макаров Ю.Н. Методика выбора варианта организации материально-технического обеспечения космических войск // Сборник научных трудов. - СПб.: Изд-во ВКА им. А.Ф. Можайского, 2010. - С. 157-164. - 0,3 п.л. (авт. вклад - 0,1 п.л.).
• Радионов Н.В. Разработка методики определения первоначальной стоимости ВВТ КВ, на которую отсутствует бухгалтерская документация // Исследование экономических проблем строительства КВ на период до 2011 г.: Отчет № 9903 МО РФ 4ЦНИИ, Шифр Полномочие-228 КВ. - М.: Изд-во ЭКА, 2008. - 8 п.л.
• Радионов Н.В. Разработка методики технико-экономического обоснования стратегии развертывания спутниковой системы с учетом новых возможностей космодромов РФ // Разработка математических моделей для программно-методического комплекса информационной поддержки эксплуатации объектов наземной космической инфраструктуры для подготовки и переподготовки специалистов ракетно-космической промышленности: Отчет 2М №0911 МО РФ ВКА им. А.Ф. Можайского шифр Эксплуатация КТ-2-ВКА. - СПб.: Изд-во ВКА им. А. Ф. Можайского, 2009. - 5,5 п.л.
• Радионов Н.В. Методика выбора вариантов стратегии развертывания орбитальных систем космических аппаратов, оптимально сочетающая качество решения социально-экономических, научных и оборонных задач и цену доставки космических аппаратов на орбиты // Разработка методик технико-экономического обоснования вариантов перспективных проектов и координации работ, связанных с созданием космических систем различного назначения: Отчет 2М №1034 МО РФ ВКА им. А.Ф. Можайского шифр Координатор-ВКА. - СПб.: Изд-во ВКА им. А. Ф. Можайского, 2010. - 1 п.л.

     Авторефераты по всем темам  >>  Авторефераты по экономике