 Все научные статьи
Все научные статьи
Пономарев Е.А., Седых П.А., Магер О.В., Урбанович В.Д. Условия возбуждения магнитосферной конвекции электрическим током, генерируемым в головной ударной волне
Научная статья
Электронный журнал ИССЛЕДОВАНО В РОССИИ
996
Условия возбуждения магнитосферной конвекции электрическим током, генерируемым в головной ударной
волне.
Пономарев Е.А., Седых n.A.fpvlsd@iszf.irk.ru), Магер О.В., Урбанович В.Д.
Институт солнечно-земной физики СО РАН, Иркутск, Россия
Абстракт.
В работе анализируются последствия генерации электрического тока на фронте Головной Ударной Волны (ГУВ) и зависимость направления этого тока от ММП. Обсуждаются условия замыкания этого тока через тело магнитосферы. Показано, что процесс проникновения стороннего тока в замагниченную плазму носит двухстадийный характер. Вначале, при изменении тока на границе возникает область поверхностного заряда, поле которого поляризует пристеночный слой толщиной порядка гирорадиуса протонов. В процессе поляризации формируется ток смещения, который образует амперову силу, ускоряющую плазму внутри двойного слоя. Когда скорость плазмы достигает скорости электрического дрейфа, (за время порядка обратной гирочастоты протонов), электрическое поле в ней исчезает, а в неподвижной системе координат, наоборот - достигает равновесных значений. Фронт изменения электрического поля проникает в плазму со скоростью быстрой магнитозвуковой волны. Изменение поля скоростей конвекции вызывает перераспределение плазменного давления. Появление соответствующих градиентов означает проникновение тока в плазму. Градиенты изменяются до тех пор, пока не установится новое стационарное состояние, которому соответствует новое поле скоростей конвекции и новое поле давления плазмы. Это новое состояние устанавливается за время Т2, которое оценивается. Для понимания зависимости конфигурации конвекции от направления внешнего тока, то есть от знака Bz -компоненты ММП, использована идеализированная модель магнитосферы в виде ограниченного в пространстве магнитного диполя с неэквипотенциальными силовыми линиями. Обсуждается вопрос о пределах применимости этой модели. Показана связь между мощностью, рассеиваемой внутри такой модельной магнитосферы и параметрами существующей в ней конвекции плазмы. Показано, в частности, что при южной В2-компоненте ММП конвекция должна быть двухвихревой, а при достаточно длительном существовании Bz ММП северного направления магнитосферная конвекция должна приобрести четырехвихревой характер. Дается оценка времени перехода от одного типа конвекции к другому.
Электронный журнал ИССЛЕДОВАНО В РОССИИ
997
ПОСТАНОВКА ЗАДАЧИ.
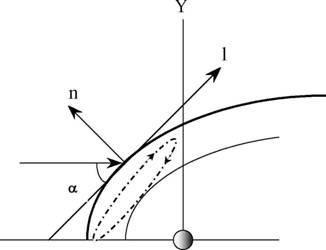
Головная Ударная Волна (ГУВ), отделяющая область Солнечного Ветра (СВ) от Переходного Слоя (ПС) является, как показано в [7,8] трансформатором, преобразующим кинетическую энергию солнечного ветра в электрическую. В результате под сводом ударной волны образуется токовый слой, отделяющий область Межпланетного Магнитного Поля (ММП) солнечного ветра от магнитного поля переходного слоя. Если вертикальная компонента ММП в солнечно эклиптической системе координат, Bz < 0, то ток под сводом ГУВ течет по часовой стрелке, если Bz>0, то - против. На рисунке 1 показан фрагмент головной ударной волны, переходного слоя и носовой части магнитосферы. Плоскость рисунка совпадает с плоскостью XY магнитосферной системы координат. Для удобства введена так же локальная система координат l,n,z, ось 1 которой направлена против потока плазмы в ПС, ось п - по нормали к линиям тока, так чтобы вместе с осью z образовать левостороннюю систему координат.
Все функции или параметры в СВ имеют индекс 0, в ПС -1 , а в магнитосфере -2, так что массовая скорость vo, vi, и V2 - это скорость плазмы в солнечном ветре, переходном слое и магнитосфере, соответственно.
Головную ударную волну мы будем аппроксимировать гиперболоидом вращения. Это не слишком хорошее приближение в смысле точности, но зато очень простое. Итак:
g = [k2(x-c)2-b2]1/2,а (1)
где г = [ х2 + g2]1/2, g2 = у2 + z2, к = Ь/а, с2 = а2 + b2; а, Ь, - полуоси гиперболоида с началом координат в фокусе.
Удобно выразить эти параметры через расстояние до носовой точки, г0 = х0 и гсаа =аа Ь/ -аа расстояниеаа отаа фокус доаа поверхностиаа гиперболоид по перпендикуляру.аа Ваа безразмерныхаа величинах, аакоторыеаа уаа насаа обозначены курсивом, например а = а/х0:
а = 1/[гс -2], Ъ =гст /[гс - 2]1/2, с = (гс-1)/(гс - 2)аа (2)
Обозначим угол между осью х и касательной к поверхности гиперболоида через а. Тогда: dr/dx=tga. Угол а меняется от л/2 до предельного значения а* = arctg(b/a), соответствующего асимптоте. Поскольку а* - угол Маха (практически мы здесь будем использовать Альфвеновский Мах):
sin а* = v0/VA = М"1, (3)
то параметры гиперболоида можно выразить также и через число Маха.
Электронный журнал ИССЛЕДОВАНО В РОССИИ
998
Bow shock Magnetopause
X
|
Bow shock Х>Magnetopause |
X
Рис.1. Расположение головной ударной волны(ГУВ), переходного слоя(ПС), магнитопаузы(МП). Если распределение полного (газовое+динамическое) давления по поперечному сечению ПС имеет максимум, то магнитосфера может "завернуть лишний ток" в переходном слое.
Электронный журнал ИССЛЕДОВАНО В РОССИИ
999
В некоторых случаях удобно использовать классическое уравнение для гиперболоида вращения:
г = у0/(1 + е coscp), (4)
где ф - угол между радиусом - вектором, направленным из начала координат в данную точку поверхности гиперболоида вращения, уо - расстояние от начала координат до поверхности гиперболоида в плоскости х=0, е =(уо - х0)/х0 -эксцентриситет гиперболоида, х0 - расстояние от начала координат до носовой точки ГУВ.
При переходе через фронт ударной волны, параметры плазмы модифицируются в соответствии со следующими соотношениями[1]:
Bno= Bniа (5)
PoVnO = PlVnl (6)
VnoBso - VsoBno = VniBsi - VsiBno (7)
PoVno2 = PoVnOVnl + Pi + Bsi2/87T (8)
PoVnOVso - Bn0Bs0/47r = poVnoVsi - Bn0Bsi/47Tа (9)
PoVno (v02 - V!2)/2аа = [уР1/(у- 1) + Bsl2/4:r] vnlа (10)
гдеаа индексыаа nа иа sаа обозначаюта нормальнуюаа илиа тангенциальную составляющие поля по отношению к поверхности гиперболоида - фронту ГУВ. В (8)-(10) учтено, что газовое и магнитное давление в солнечном ветре много меньше динамического. Из (7) и (9) находим:
Bsl = Bs0 а [1- Bno2/47rpoVno2]/[l-aBn02/47rpoVno2]аа (11)
vsi = vs0 -аа vn0(c) - l)Bs0Bno/47rp0vno2[l-C)Bno2/47rpovno2] (12)
Здесь под а подразумевается отношение (vn0/vni). Видно, что с ростом нормальной компоненты магнитного поля появляется опасность возникновения особенности в (11) и (12). Избежать бесконечного увеличения тангенциальных компонент магнитного поля и скорости за фронтом ударной волны можно, если устремить а к 1. Но тогда, по существу, исчезает ударная волна. Переход через фронт не сопровождается скачком скорости, плотности и т.д. По существу проблема сводится к отысканию величины скачка плотности или нормальной компоненты скорости течения при переходе через ударный фронт. Пусть a = Vno/vni, тогда исключив pi из (8) и (10), используя (11) и (12) найдем уравнение для а:
(a -l)(a-a*)(Mn2-a)2-a2(a-l)(Mn/Ms)2 - 2ctga-a2(a-l)(Mn2-a)(Mn/Ms)+
+(2-у)/(у-1>[а3 (Mn2 -l)2 ]/Ms2 = 0 (13)
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1000
Здесь приняты следующие обозначения:
Mn2 = (B0/Bn0)2M2sin2a,аа Ms2 = (B0/Bs)2M2sin2a.а (14)
В0 - значение модуля полного вектора магнитного поля солнечного ветра; Вп0-значение нормальной составляющей магнитного поля солнечного ветра в локальной системе координат (по оси n); Mn, Ms и М - локальные числа Маха и число Маха-Альфвена, соответственно; а* =(у+1)/(у-1). Остальные обозначения соответствуют ранее принятым. Из (13) видно, что при больших значениях Mn a=a*, а при Мп => а, сама а стремится к 3! Замечательно, что именно такое значение имеет а*, когда показатель адиабаты у становится равным двум, как для газа с двумя степенями свободы.
ПРОНИКНОВЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА В МАГНИТОСФЕРУ И ФОРМИРОВАНИЕ КОНВЕКЦИИ.
В локальной системе координат компоненты магнитного поля имеют вид:
Вц= a[Bx0cosa + (By0sim> Bz0cosu)sina]аа (15)
Bnl=аа Bx0sina - (Byosinu - Bz0cosu)cosa (16)
BTi= a[By0cosu + Bz0sinu], (17)
здесь и - угол между плоскостью {x,z} магнитосферной системы координат и плоскостью {1,п} локальной. Взяв ротор от магнитного поля в локальной системе координат, мы получим значение плотности тока в этой системе. В данном случае нас интересует только нормальная составляющая:
jm = с/4тг[авт1/а1 - авц/дт]аа (18)
Посколькуаа BTiаа неаа зависитаа отаа переменных,аа связанныхаа саа 1аа -координатой (например с а), то первый член в квадратных скобках в (18) равен нулю. Поскольку dx = gdu, для плотности нормального тока имеем:
jni= -(ca/47rg)-[By0cosD + Bz0smu]sina ,аа (19)
9аа 9аа 1/9
где g =(у + z ) определяется уравнением (1).
Таким образом, мы получили выражение для плотности электрического тока, который формируется под сводом головной ударной волны и направлен во внутрь полости, образованной ГУВ. По всем признакам, это тот самый ток, который питает электромагнитной энергией магнитосферные процессы. Во-первых, он зависит от Ву и Bz компонент ММП, во-вторых, он имеет составляющую утро-вечер, которая зависит только от Bz и составляющую север-юг, зависящую только от Ву. Именно такую связь с Ву ММП обнаруживают геомагнитные вариации [4]. В-третьих - численная оценка jni дает при a = 4, g = 10 см и В0 ~ 5 пТ значение плотности тока соответствующее значению плотности тока утро-вечер в эмпирических моделях [6]. На первый
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1001
взгляд, выражение (19) имеет неустранимую особенность при gЧ0, то есть в носовой точке. На самом деле это не так. Формула (19) описывает сразу два тока - выходящий под углом 7г/2- а и входящий под углом -(л/2- а) к оси х. При малом g разница этих углов тоже мала. В пределе эти, противоположно направленные токи совпадают, и результирующий ток отсутствует. Ясно, что при малых g токи замыкаются в переходном слое и не проникают в магнитосферу(рисЛа). Поэтому, следует ввести некоторый параметр -наименьшее значение gm , начиная с которого формула (19) применима для магнитосферы. Самый простой выбор: gm= d, где d - толщина ПС в носовой точке.
Прежде чем попасть в магнитосферу, ток jnl должен пройти переходный слой и, следовательно, необходимо обсудить вопрос о взаимодействии этого тока с плазмой ПС. По смыслу он играет роль нагрузки, которой сообщается часть электрической мощности, но может выступить и в качестве генератора, включенного последовательно. Все зависит от знака скалярного произведения в правой части уравнения:
pvdv/dt + vVp=jE (20)
Если jE >0, то имеет место потребление электромагнитной энергии в системе, если же jE<0, то , наоборот, генерация. Второй член в левой части равенства однозначно является генератором, поскольку vVp <0. Первый член -потребитель энергии, так как в процессе движения плазмы ПС по зазору между фронтом ГУВ и магнитопаузой ее кинетическая энергия растет. Таким образом, вопрос о том, будет ли плазма ПС генератором или нагрузкой зависит от соотношения величин первого и второго членов левой части (20). В работе [8] мы показали, что при определенных допущениях о вкладе свежей плазмы (т.е. только что проникшей через фронт в ПС), левая часть (20) может работать как генератор. Конечно, опираться на допущения всегда нежелательно. Поэтому, мы в данной работе вычислили jni непосредственно из значений трансформированного магнитного поля. В такой постановке задачи роль инерционного члена оказывается чисто пассивной. При отсутствии тока плазма ускоряется только за счет падения давления вдоль ПС, а при наличии тока - "доускоряется". При этом набор кинетической энергии не зависит от направления тока.
В то же время ясно, что магнитосфера не может получить ток больший, чем произведен ГУВ.
Коротко обсудим условия, которые должны удовлетворяться для прохождения тока внутрь магнитосферы. Пусть в исходном состоянии электрический ток однороден и направлен вдоль оси у. Если в некоторый момент ток j0 увеличится на Sj вне нашего объема, то на его границе начнет образовываться заряд с поверхностной плотностью: jli = j" Sj dt. Образующееся при этом электрическое поле Е вызовет появление тока смещенияа jc = (s/4n)-dE/dt,
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1002
создающего амперову силу, которая уравновешивается только силой инерции, поскольку соответствующий градиент давления еще не успел сформироваться:
p0dv/dt=[jcxB]/cаа (21)
9а 9
В условиях магнитосферы диэлектрическая проницаемость плазмы s = с / Va , тогда интегрирование (21 ) дает:
v = с[Е х В]/ В2 ,аа (22 )
( с учетом того, что квадратами возмущенных величин можно пренебречь, как имеющими второй порядок малости).
Физический смысл изложенного заключается в том, что электрическое поле
поляризации возникает внутри двойного слоя толщиной порядка ?, = 27гс8/сов =
с/сОрр , где cs - скорость быстрой магнитозвуковой волны, сорр - протонная
плазменная частота (такая толщина характерна для токовых слоев в
бесстолкновительнойаа лабораторнойаа иаа космическойаа плазме) Ваа процессе
становления это поле образует ток смещения, формирующий амперову силу, которая ускоряет плазму внутри этого слоя. Тогда как в процессе становления электрическое поле в системе координат плазмы падает до нуля, в лабораторной оно, наоборот, растет от нуля до величины [VxB]/c.
Поскольку после релаксации поля внутри элементарного слоя граница с поверхностным зарядом сместилась внутрь плазмы ( за время ii ~ 27г/сов ) на расстояние порядка ?,, то все вышеописанное повторяется. Очевидно, это означает проникновение импульса, связанного с электрическим полем, внутрь плазмы со скоростью звука. Так начинает формироваться конвекция (см. рис.2). Если в плазме нет потерь и divV=0, то на этом дело и заканчивается. Плазма получает импульс от электрического поля, соответствующий скорости установившейся конвекции.
Стационарный электрический ток при этом не возникает. Но если объем ограничен стенками, или в нем имеется неоднородное магнитное поле, то первичная конвекция перестраивается. При этом может образоваться градиент давления, существование которого означает, что в плазме возникает электрический ток. Это и означает проникновение внешнего тока в плазму. Рассмотрим теперь формирование градиента давления из-за сжимаемости газа. Из уравнения непрерывности:
p' = -p0jdivVdtа (23)
Интегрирование ведется по всему времени формирования конвекции Т2 Поэтому можно записать (23) в виде:
р' = Ро (VVpB/pB)x2 ~ Po(V/Lb)t2а (24)
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1003
уаа J2h
*'а Магнито пауза
Плазма
'3h
E=-[VB]/c
'см
С/Q
С
ms
т
Рис.2.а Схема проникновения стороннего тока в плазму и возбуждение магнитосферной конвекции.
ровнойа здание

Рис.3. Схема расположения функциональных блоков в магнитосфере:
I -а МГД-генератор, преобразующий кинетическую энергию солнечного
ветра в электромагнитную;
IIа - МГД-компрессор, преобразующий электрическую энергию в газовое
давление.
III - вторичные МГД-генераторы, преобразующие энергию сжатого газа
в электрический ток, питающий электроджеты в ионосфере.
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1004
Возмущение давления р' находим из уравнения состояния:
Р' = cs2 р\а (25 )
здесь cs - скорость быстрой магнитозвуковой волны, поскольку магнитная упругость очень существенна в магнитосфере.
С учетом того, что скорость быстрого магнитного звука в магнитосфере практически равна альфвеновской скорости, находим:
Vp' ~ -р0 cs2Vt2/L2~ F ,аа (26)
где F - амперова сила. Поскольку V ~ Fii /р0, то из (26) следует:
Tii2 = L2/cs2 (27)
Это соотношение связывает размеры системы с временем установления стационарного распределения давления - формированием градиента газового давления. Последний, как мы знаем, определяет ток в плазме.
Иначе говоря, Т2 является характерным временем проникновения электрического ток в плазменный объем. Принимая для ii = соваа ~ lc, L ~ 10а см,аа для cs ~ 3
о
10 см/с, то для i2 находим время -1000 секунд. Такая длительность переходного процесса для магнитосферы не вызывает возражений. Получается, что наша система имеет три характерных времени: ti=27t/co, характеризующее время становления электрического поля в точке, тг - время проникновения электрического тока в объем и время тз = L/cs - время установления электрического поля в системе с размером L. Следует отметить, что градиент газового давления формируется и в том случае, если магнитное поле однородно, но есть стенка, ограничивающая движение плазмы. При этом (27) имеет тот же вид, а время Т2 приобретает наглядность. Это просто время заполнения объема между стенкой и точкой, находящейся на некотором расстоянии от стенки плазмой, двигающейся со скоростью V в направлении стенки.
Из сказанного выше следует важный физический вывод. Процесс проникновения тока в плазму является двухступенчатым. Сначала формируется поле поляризации, которое послойно проникает в плазму. Точнее, в плазму проникает соответствующий этому полю импульс. Затем, если система неоднородна, течение может перераспределить давление так, что в плазме из-за появления градиентов возникнет электрический ток. С энергетической точки зрения этот ток необходим для поддержания конвекции в неоднородной системе. В самом деле, из соотношения:
VVp = Ej,
(28)
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1005
следует, что ток необходим для поддержания течения в неоднородной среде.
Еслиаа мыаа проинтегрируемаа (28)аа поаа объемуаа системы,аа тоаа убедимся,аа чтоаа в стационарном случае потребляемая мощность:
W = J uVVp dU = J udivS dU =J ф dZ = J xyj dZ, (29)
где U и Z объем и площадь поверхности нашей системы, \|/ - потенциал поверхности. Очевидно, что если поверхность замкнута и эквипотенциальна, т.е. V|/ можно вынести за интеграл, то система энергетически изолирована от окружения - туда не может быть закачена (или оттуда выкачена) энергия, поскольку v|/J х jdZ =0. Это было показано Хеккилой [5]. Используем (29) для оценки мощности, вносимой в магнитосферу нашим током при соответствующей разности потенциалов. При А\|/ ~ 600 CGSE (это -120 кэв.) и jni~5-10"5 CGSE и Z ~ 10 см , получим для W величину порядка 3-10 эрг/с, что соответствует величине, принятой для возмущенного состояния магнитосферы. Как мы не раз подчеркивали, уравнение (28) имеет глубокий физический смысл. Если Ej>0, то электрические силы производят работу над плазмой. Она в этом случае, движется в сторону повышенного давления, то есть сжимается. В другом случае расширяющийся газ производит электрическую мощность. В магнитосфере есть как МГД-компрессоры, так и МГД - генераторы (см.рис.3)[3,7]. Если бы их совокупная производительность была бы одинакова, то энергетический баланс был бы нулевой и магнитосфера не нуждалась бы во внешних источниках энергии. На самом деле внутри магнитосферы находится постоянный потребитель энергии - ионосфера Земли. Известно, что плотность потока энергии через поверхность пропорциональна компоненте электрического поля касательной этой поверхности. Очевидно, что таким образом, меняя степень неэквипотенциальности магнитопаузы, магнитосфера может регулировать поступление энергии извне. Этот вопрос важен вот в каком отношении. Можно представить себе, что интенсивность магнитосферных процессов определяется только мощностью, предлагаемой внешним источником. Но можно так же допустить, что существует и некий регулятор, который пропускает лишь определенную часть предлагаемой мощности. Если этот регулятор еще и связан с потребителем, то мы получаем очень устойчивую природную систему. Ниже мы еще коснемся этого процесса и рассмотрим его на простом примере.
Единственной задачей рассмотрения такого примера является прояснение роли электрическогоа потенциала,а задаваемогоа наа стенке,а ва вопросеа энергообмена модельнойа магнитосферыа са окружением.а Подобнаяа модельа широко использовалась Ю.А. Ромащенко для анализа магнитосферных процессов [2]. Пусть магнитное поле диполя ограничено в пространстве наложенным на него постоянныма магнитныма полем,а имеющима однуа вертикальнуюа компоненту 2MJxJ. Тогда:
Электронный журнал ИССЛЕДОВАНО В РОССИИ 1006аа Ве=аа Msinu(l+2r3/r003)/r3, (31)
где г, - радиус полости, в которой определено магнитное поле - радиус нашей модельной магнитосферы, и - коширота.
В такой модели возникают трудности, связанные с тем, что магнитные силовые линии (МСЛ), выстилающие поверхность сферы г = г, сходятся в одной точке. Таким образом, либо сфера должна быть эквипотенциалью, либо должно быть введено затухание потенциала вдоль магнитных силовых линий. Обычно выбирается первый вариант преодоления упомянутой трудности. Но этот выбор влечет за собой неприятное следствие: в полость, окруженную непрерывной эквипотенциальной поверхностью, электромагнитная энергия извне попасть не может [5]. Поскольку мы моделируем обмен энергией магнитосферы с окружением, нам этот вариант не подходит. Но если мы останавливаемся на втором варианте разрешения парадокса, то есть требуем затухания поля вдоль МСЛ, то нам не обязательно исследовать распределение потенциала внутри сферы. Мы можем заменить ее цилиндром, в котором потенциал падает от экваториальной плоскости по экспоненте. Тогда и решение для поля можно искать в цилиндрической системе координат, что гораздо проще. Решение для электрического потенциала V|/ в этом случае имеет вид:
V = H'oJn (kr)exp(-kz +тф),аа (32)
где Jn - функция Бесселя, п- номер гармоники азимутальной компоненты, "вертикальное волновое число", определяющее скорость убывания потенциала от плоскости XY. Далее мы будем полагать, что п = 1, a z = 0. Тогда компоненты электрического поля в экваториальной плоскости будут:
Ег = Е0 [Ji/kr - J0] sincp,аа г < Гооа (33)
Еф = -E0JiCOS(p /kr , (34)
где Е0 = ik\\f0
А соответствующие компоненты скорости конвекции в экваториальной плоскости будут:
Vr = -VoX-4JiCosq) /[1 + 2Х3/(Хоо)3]а (35)
УФ = -VoX-3 [J(X)/X - Ji( X)] sinq> / [1 + 2X3 l{U\(36)
здесь x = kr Уравнение магнитной силовой линии для нашей магнитосферы будет:
sin и = Lаа -(1-L /Loo)аа ,
(37)
Электронный журнал ИССЛЕДОВАНО В РОССИИ 1007 
270
Рис.4. Распределение линий конвекции в магнитосфере, согласно уравнению (38): а) двухвихревой при Bz<0; б) четырехвихревой при Bz>0.
Электронный журнал ИССЛЕДОВАНО В РОССИИ
где L - эль- параметр Мак-Илвейна. Поскольку для плазмы, энергия частиц которой достаточно мала в том смысле, что магнитный дрейф для них не существенен, потоковые линии конвекции совпадают с изолиниями равного потенциала, уравнение линий конвекции будет просто:
Ji(x) sin ф = const = Gаа (38)
На рисунке 4а и 46 представлено распределение линий конвекции для нашей
модели,а дляа случаев,а когдаа границаа модельнойа магнитосферыа -
эквипотенциальна,
а Хоо равно соответственно 4( рис 4а) и 7(рис.4б).
Для того, чтобы поток вектора Пойнтинга через поверхность нашей модельной
магнитосферы был отличен от нуля, необходимо, чтобы существовала отличная
от нуля тангенциальная компонента электрического поля Ефа Иначе говоря,
J^kXoo), а следовательно и i^kr,) не должны быть равны нулю.
Поскольку электрическое поле в модели нам известно, а внешний
электрический ток задается нами иза модели Головнойа Ударной Волныа и
Переходногоаа Слоя,аа кака источниковаа этогоа ток [8],а тоа мыаа можема найти
электрическую мощность, потребляемую нашей модельной магнитосферой:
W = JJ\|/0Ji(xл)jrrл2sinusin(pdod(p, (39)
где интегрирование по и ведется в пределах от 0 до 2л, а по ф - от -nil до nil. Поскольку:
jr=-jnisin(a+(p),аа (40)
а jni дается (19), то (39) можно проинтегрировать, учитывая, что а может быть выражено через ф, поскольку tga + ^ф = - е СБСф, где е =(у0 - х0)/х0 -эксцентриситет параболы. Решение (39) при условии (40) имеет вид:
W = (3/34у0) caw-oo2Ji(Xoo)B0zа (41)
Считается, что W >0 если мощность производится в объеме, если же мощность потребляется, то W<0. Условимся, что магнитосфера может быть только потребителем мощности, тогда у нас JiB0z<0. Это значит, что при отрицательном B0z, функция Бесселя должна быть положительна, то есть 0<Хоо<4. Наоборот, при B0z>0 функция Бесселя должна быть отрицательна и тогда 4<Хоо<7. Как мы уже видели на рисунках 4а и 46 конвекция при этом будет двухвихревой в первом случае и четырехвихревой во втором. Формально W(Xoo) описывает зависимость реализуемой в магнитосфере мощности стороннего тока от Хоо- Но поскольку эта мощность определяется процессами, идущими внутри магнитосферы (в особенности - джоулевыми потерями ионосферных токов, а так же высыпаниями частиц из магнитосферы),
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1009

"0.4а "0.2аа 0а 0.2а 0.4а 0.6
L-0.346Jаа W(x)а L0.582J
W-10"18 эрг/с
Рис.5. График функции Xoo(W)[npn Av|/ ~ 600 CGSE (~ 120 кэв) и jni~5-10" CGSE]. Функция W(Xoo) описывает зависимость реализуемой в магнитосфере мощности внешнего тока от х<.
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1010
то W является заданным аргументом, а х _ее функцией. Иначе говоря, безразмерный радиус нашей модельной магнитосферы задается мощностью происходящих в ней потерь! Поскольку, физический радиус г, задается из других соображений (баланса давления, например), то фактически определяется зависимость от W параметра к. На рисунке 5 приведена зависимость Xo(W).
Из рисунка видно, что функция X<(W) многозначна. Одному и тому же значению -W>0 и -W<0 соответствуют две пары значений %<. При х<х> около 2 функция W имеет максимум, а при хо около 4 проходит через ноль. Интересно отметить, что именно при х<х> около четырех, конвекция приобретает законченную двухвихревую структуру. При Хоо>4 наблюдается переход от двухвихревой к четырехвихревой структуре, которая полностью развивается при Хоо = V. В двухвихревом варианте изменение направления конвекции без превращения магнитосферы из потребителя энергии в генератор возможно лишь при одновременном изменении градиентов давления на обратные. Но такая операция требует полной перестройки рельефа давления. Естественно, что такое перераспределение давления требует совершения определенной работы или предоставления газу возможности совершить работу над электромагнитными силами. Для этого на ночной стороне газ должен совершить работу над электромагнитным полем, а на дневной, наоборот электромагнитные силы должны совершить такую же работу над газом. На перестройку должно быть затрачено время. По порядку величины мы можем его оценить:
T=A/W* ,а (42)
где А ~{<р> dU, <р> - средняя величина газового давления в магнитосфере, U -объем магнитосферы,а W* - мощность магнитосферного процесса, соответствующего такой перестройке. При U~ 4-1030см3 , <р> ~ 3-10"9эрг/см3, А-1.2 -1022 эрг, W*~ 3-1016эрг/с доя
17аа 1Я
спокойных условий, 10 эрг/с для умеренно возмущенных и W*~ 10 эрг/с доя суббури, получаем характерное время существования перестроечного режима порядка 132 часов, 33 часов и 3.3 часа, соответственно. Естественно, что в течение всего этого времени Bz ММП, а значит и jni должны оставаться положительными. Как мы уже говорили, доя этого режима характерно изменение знака внешнего тока с положительного на отрицательный. Однако, рельеф газового давления, а следовательно и внутримагнитосферные токи не могут перестроиться так быстро. Создается ситуация, в которой внешний ток (в отличие от электрического поля) не может проникнуть внутрь магнитосферы(там неподходящие градиенты давления!), по крайней мере, в течение оцененного выше времени, тогда как электрическое поле должно поменять знак. Однако, по непонятной нам еще причине, такая перемена знака поля происходит не во всей магнитосфере, а лишь во внешней ее части. Возможно, полного обращения конвективного движения во всей магнитосфере
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1011
никогда неа происходит,а аа оноа происходит толькоа на периферии,а путем возникновения четырехвихревой системы.
На рисунке 4 показаны случаи, когда граничная поверхность гю совпадает на экваторе с эквипотенциалью, то есть х ~4. Как отмечалось выше, это соответствует случаю, когда энергообмен модельной магнитосферы с окружением отсутствует. Поскольку наша модельная магнитосфера является потребителем электрической мощности, то реальная граница должна проходить либо внутри показанной области, так, например, как пунктирный круг, или вне ее, если ММП B0z>0.
ВЫВОДЫ.
Приведенные выше аргументы позволяют сделать следующие заключения. Головная ударная волна может быть источником мощности, достаточным для энергообеспечения суббуревых процессов. Направление тока за фронтом ГУВ зависит от знака Bz - компоненты ММП. При Bz <0 ток в цепи "головная ударная волна-магнитосфера" течет по часовой стрелке, то есть в ночной части магнитосферы. Это ток утро-вечер, при Bz >0 он меняет направление на обратное.
Всякое изменение внешнего тока через магнитосферу вызывает перестройку конвекции за время порядка времени пробега магнитозвуковой волны от магнитопаузы до центра системы, поскольку волна перестройки идет от обоих флангов. В нашей модели это отражается в переходе от двухвихревой к четырехвихревой системе конвекции. При этом энергетические возможности для внутримагнитосферных процессов сильно сокращаются. Пока не установилось новое распределение газового давления, роль силы, противостоящей силе Ампера берет на себя сила инерции. Это соответствует ускорению плазмы, а следовательно, изменению электрического поля. По нашему мнению, имеет смысл попытаться наблюдать волну перестройки в высоких широтах на радарах системы SuperDARN или на телевизионных системах с большим углом зрения. На примере простой (лквазисферической) модели замкнутой магнитосферы исследована зависимость конфигурации конвекции от знака Bz ММП и потребления мощности магнитосферно-ионосферной системой. Показано, как при достаточно длительном существовании северной Bz ММП, двухвихревая система конвекции переходит в четырехвихревую. В рамках модели получено выражение, связывающее потребляемую мощность с величиной вертикальной составляющей ММП. Эта мощность зависит от напряженности межпланетного магнитного поля в первой степени. Работа выполнена в рамках проекта РФФИ № 02-05-64066, № 03-05-06477.
Электронный журнал ИССЛЕДОВАНО В РОССИИ
1012
ИТЕРАТУРА.
[1]. Коробейников В.П. Задачи теории точечного взрыва. М.: Наука,а 1985.
С.400.
[2]. Ромащенко Ю.А. Влияние динамики солнечного ветра на магнитосферные
процессы и их геофизические проявления. Диссертация на соискание ученой
степени доктора физико-математических наук. Якутск, 1992.
[3]. Седых П.А., Пономарев Е.А. Магнитосферно-ионосферное взаимодействие в
области авроральных электроджетов.// Геомагнетизм и аэрономия, 2002. Т.42. №5.
-С.613-618.
[4]. Уваров В.М., Барашков П.Д. Типы распределения электрических полей и
соответствующиеаа имаа типыаа конвекцииаа ваа полярнойаа ионосфере.аа Модель.//
Геомагнетизм и аэрономия, 1989. Т. XXIX. № 4. С. 621-628.
[5].а Heikkila W.J.а Interpretation of recent AMPTE data at the magnetopause.//J.
Geophys.Res., 1997. V.102. A2. - P.2115-2124.
[6]. Mead G.D., Fairfield H.D. A quantitative magneto spheric model derived from
spacecraft magnetometer data.//J. Geophys. Res., 1975. Vol.80, P.523-534.
[7]. Ponomarev E.A. On one plausible simple explanation for substorm break-up // Proc.
5-th International conference on Substorms, ESA SP-443, 2000. - P. 549.
[8]. Ponomarev E.A., Urbanovich V.D., Nemtsova E.I. On the excitation mechanism of
magnetospheric convection by the Solar Wind // Proc. 5-th International conference on
Substorms. ESA SP-443. 2000. P. 553.
 Все научные статьи
Все научные статьи

